ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 462
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Шығармашылық топ автор-қҧрастырушылар:
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
2 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
3 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«СТАТИСТИКА ЭЛЕМЕНТТЕРІ» бөлімі бойынша жиынтық бағалау
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР.
1 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
Ойлау дағдыларының деңгейлері: Қолдану
2 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
АРАСЫНДАҒЫ ҚАТЫСТАР» бөлімі бойынша жиынтық бағалау
3 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
4 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
ТОҚСАНДАҚ ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР. Алгебра
Ойлау дағдыларының деңгейі: Қолдану
-
[4 a a] АВСDпараллелограмыныңАDқабырғасынан Eнүктесіалынған, ∠ВED
= 900 , ∠EВD= 450 , АЕ= 4 см, ЕD= 9 см. Параллелограмм ауданын табыңыз
-
[4 a a] АВС үшбұрышының ауданы 36 см2. АВ = 4 см, АС = 9 см. ВАСбұрышыныңшамасынтабыңыз.
-
[7 a ] Тең бҥйірлі трапециясының диагоналі бҥйір қабырғасына перпендикуляр. Егер ҥлкен табаны 4√3 , ал трапецияның бір сҥйір бҧрышы 600 болса, трапеция ауданын табыңыз.
Балл қою схемасы
| № | 1 нҧсқа | 2 нҧсқа | Балл |
| 1 | В | В | 1 |
| 2 | қабырғасы 30 см кадрат пішіндес тақтайшалармен жабуға болады | қабырғасы 25 см кадрат пішіндес тақтайшалармен жабуға болады | 1 |
| Ӛз жауабын тҥсіндіреді | Ӛз жауабын тҥсіндіреді | 1 | |
| 40 тақтайша | 80 тақтайша | 1 | |
| қабырғасы 25 см кадрат пішіндес тақтайшалармен жабуға болмайды | қабырғасы 30 см кадрат пішіндес тақтайшалармен жабуға болмайды | 1 | |
| 3 | Есеп шартына сәйкес суретті салады | Есеп шартына сәйкес суретті салады | 1 |
| ∆АВD –теңбҥйірлі екенін дәлелдейді | ∆АВD- теңбҥйірлі екенін дәлелдейді | 1 | |
| ВЕ=8 см | ВЕ=9 см | 1 | |
| SАВСD= 11⋅ 8 = 88см2 | SАВСD= 13⋅ 9 = 117см2 | 1 | |
| 4 | S=1 ???? формуласын 2 қолданады | S=1 ???? формуласын 2 қолданады | 1 |
| 24=1 · 3 · 8 · ????i???? BAC 2 | 36=1 · 4 · 9 · ????i???? BAC 2 | 1 | |
| sin ∠BAC=0,5 | sin ∠BAC=0,5 | 1 | |
| ∠BAC= 30 0 | ∠BAC = 30 0 | 1 | |
| 5 | Есеп шартына сәйкес суретті салады | Есеп шартына сәйкес суретті салады | 1 |
| 30 0 туралы теореманы қолданады, бҥйір қабырғасын табады | 30 0 туралы теореманы қолданады, бҥйір қабырғасын табады | 1 | |
| Жоғарғы табыны, диагоналі мен бҥйір қабырғасы арқылы жасалған шбҧрыштың тең бҥйірлі екенін дәлелдейді және 4√3 кіші табанын табады | Жоғарғы табыны, диагоналі мен бҥйір қабырғасы арқылы жасалған шбҧрыштың тең бҥйірлі екенін дәлелдейді және 2√3 кіші табанын табады | 1 | |
| Биіктікті табу әдісін кӛрсетеді | Биіктікті табу әдісін кӛрсетеді | 1 | |
| Биіктігі 6 см | Биіктігі 3 см | 1 | |
| Трапеция ауданын табу формуласын қолданады | Трапеция ауданын табу формуласын қолданады | 1 | |
| S=36√3 см2 | S=9√3 см2 | 1 | |
| Барлық балл | | 20 | |
4 тоқсан ҥшін ТЖБ
Уақыты - 40 минут
Балл саны - 20
-
нҧсқа
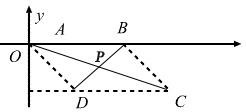1. [2 a a] (0; 0) (9; 10) нҥктелерінен ӛтетін тҥзудің теңдеуін жазыңыз 2. [3 a a] Егер (0; 0), ( 5; 0), (12; −3). болса,АВСД параллелограмының Д тӛбесінің координатасын табыңыз. Р диагональдарының қиылысу нҥктесі.
3. [4 a a] М нҥктесі РК кесіндісін Р нҥктесінен 3:1
қатынасында бӛледі. Егер М (2; -4), К (3; 5) болса, Р нҥктесінің координатасын табыңыз
4. [5 a ]
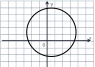
а) (???? − 3)2 + (???? − 5)2 = 49. шеңбер теңдеуін қҧрыңыз
b) (???? − 3)2 + (???? − 5)2 = 49 және ???? = −2 тҥзуінің ӛзара орналасуын анықтаңыз
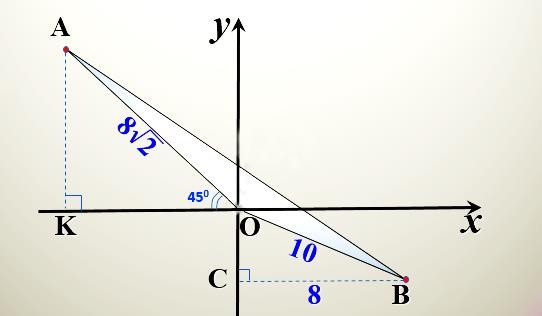5. [6 a ] Суретте ОВ=10, ОА= 8√2. ОА сәулесі ОХ осімен 450 жасайды, ал В нҥктесі ОУ осінен арақашықтығы 8.a А нҥктесінің координатасын табыңыз
b) В нҥктесінің координатасын табыңыз с). АВ кесіндісінің ҧзындығын табыңыз
-
нҧсқа
1. [2 a a] (1; 2) (−1; 1) нҥктелерінен ӛтетін тҥзудің теңдеуін жазыңыз
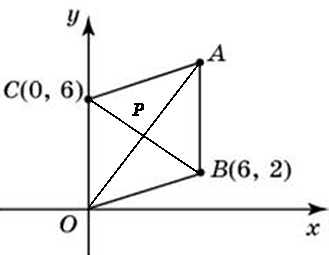
6. 2. [3 a a] Егер (0; 0), ( 6; 2),
(0; 6). болса, АВОС параллелограмының А тӛбесінің координатасын табыңыз. Р диагональдарының қиылысу нҥктесі.
3. [4 a a] М нҥктесі РК кесіндісін Р нҥктесінен 2:1 қатынасында бӛледі. Егер М(2;1), К(3;5) болса, Р нҥктесінің координатасын табыңыз
4. [5 a ]
а) (???? − 3)2 + (???? − 5)2 = 9. шеңбер теңдеуін қҧрыңыз
b) (???? + 3)2 + (???? + 5)2 = 9 және ???? = −2 тҥзуінің ӛзара орналасуын анықтаңыз
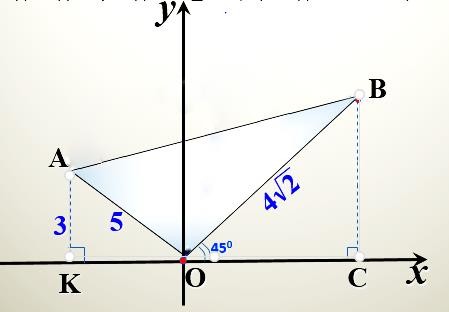5. [6 a ] Суретте ОА=5, ОВ= 4√2 . ОВ сәулесі Ох осімен 450, ал А нҥктесі Ох осінен арақашықтығы 3.a). B нҥктесінің координатасын табыңыз b A нҥктесінің координатасын табыңыз с). АВ кесіндісінің ҧзындығын табыңыз
Баллқоюсхемасы| № | 1 нҧсқа | 2 нҧсқа | Балл | |
| 1 | ???? − 0 = ???? − 0 9 − 0 10 − 0 | ???? − 1 = ???? − 2 −1 − 1 1 − 2 | 1 | |
| 10???? − 9???? = 0 | ???? − 2???? + 3 = 0 | 1 | ||
| 2 | ???? = ????????+???????? ???? = ????????+???????? ???? 2 ???? 2 | ???? = ????????+???????? ???? = ????????+???????? ???? 2 ???? 2 | 1 | |
| ????(6; −1,5) | ????(3; 4) | 1 | ||
| ???? = 7 | ???? = 6 | 1 | ||
| 3 | ????− = 3 | ????− = 2 | 1 | |
| ????????+3·3 2 = 1 + 3 | ????????+2·3 2 = 1 + 2 | 1 | ||
| ????????+3·5 −4 = 1 + 3 | ????????+2·5 1 = 1 + 2 | 1 | ||
| ????(−1; −24) | ????(0; −7) | 1 | ||
| 4 а | (3; 5) шеңбер центрі | (−3; −5) шеңбер центрі | 1 | |
| 7 радиус ҧзындығы | 7 радиус ҧзындығы | 1 | ||
 | | 1 | ||
| 4 b | | | | 1 |
| | ||||
| Тҥзу шеңберді жанайды | Тҥзу шеңберді жанайды | 1 | ||
| 5a | Ҥшбҧрыштың тҥрін анықтайды АК=КО | Ҥшбҧрыштың тҥрін анықтайды CB=CО | 1 | |
| | ????2 + ????2 = (8√2)2 ???? = ±8 | ????2 + ????2 = (4√2)2 ???? = ±4 | 1 | |
| A(4; 4) | ????(4; 4) | 1 | ||
| 5b | ????(8; 6) | A(−4; 5) | 1 | |
| 5c | Кесінді ҧзындығын табудың формуласын қоданады | Кесінді ҧзындығын табудың формуласын қоданады | 1 | |
 ???????? = 2√65 | ???????? = √65 | 1 | ||
| Барлық балл | 20 | |||