ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 447
Скачиваний: 2
СОДЕРЖАНИЕ
Шығармашылық топ автор-қҧрастырушылар:
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
2 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
3 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«СТАТИСТИКА ЭЛЕМЕНТТЕРІ» бөлімі бойынша жиынтық бағалау
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР.
1 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
Ойлау дағдыларының деңгейлері: Қолдану
2 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
АРАСЫНДАҒЫ ҚАТЫСТАР» бөлімі бойынша жиынтық бағалау
3 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
4 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
ТОҚСАНДАҚ ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР. Алгебра
Ойлау дағдыларының деңгейі: Қолдану
ТОҚСАНДАҚ ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР. Геометрия
Тоқсандық жиынтық бағалаудың мақсаты білім алушылардың тоқсан барысында меңгерген білім, білік және дағдыларын анықтауға бағытталған.
Жиынтық бағалау кҥтілетін нәтижелер жетістігін және тоқсанға жоспарланған оқу мақсаттарына жеткендігін тексереді
Білу:
-
кӛпбҧрыштар жіктемесін білу; -
жазық фигуралардың негізгі тҥрлерінің қасиеттерін және белгілерін білу. Тҥсіну: -
математиканың академиялық тілін тҥсіну; -
тҥрлі қолданбалы есептерді шешуде математикалық модельдерді пайдаланудың маңыздылығын тҥсіну; -
аксиома мен теорема сияқты математикалық категориялардың мағынасын тҥсіну; -
жазықтықтағы геометриялық салулар мен ӛлшемдердің қағидаттарын тҥсіну.
Қолдану:
-
математикалық есептерді шешу алгоритмдерін қолдану; -
геометриялық есептерді шешуде жазық фигуралардың қасиеттерін қолдану; -
тҥрлі қолданбалы есептерді шешуде математикалық модельдерді қолдану; -
тҥпмәтінге сәйкес математикалық терминологияны қолдану.
Талдау:
-
геометриялық фигуралардың ӛзара орналасуын талдау; -
математикалық модельдер қҧрастыру ҥшін мәтіндік есептердің шарттарын талдау.
Жинақтау:
-
математикалық есептерді шешудің алгоритмдерін жинақтау; -
аксиомалар мен теоремалар арқылы дәлелді пікірлерді жинақтау; -
геометриялық тҥрлендірулерді қолдана отырып қҧрастыру есептерін шешу тәсілдерін жинақтау.
Бағалау:
-
есептің тҥпмәтініне қатысты есептеулер нәтижесін бағалау.
І тоқсан ҥшін ТЖБ
Уақыты - 40 минут
Балл саны - 20
-
нҧсқа
-
[1 балл] ABCD – ромб берілген. Сбұрышынтабыңдар.
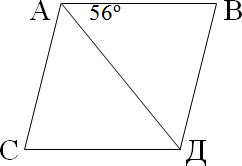 А) 34о Б) 56о В) 68о Г) 102о Д) 28о
А) 34о Б) 56о В) 68о Г) 102о Д) 28о-
[6 балл] ABCD параллелограмының биссектрисасы оның ВС қабырғасын ВК = 19 см және КС = 10 см болатын кесінділерге бӛледі. Оның перимтрін табыңдар.
-
 [4 балл]. Трапецияның бҥйр қабырғалары бірдей тӛрт бӛлікке бӛлініп табандарына пареллель кесінділермен қосылған. Егер трапеция табандары 6 м және 18 м болса, осы кесінділер ҧзындықтарын табыңыз
[4 балл]. Трапецияның бҥйр қабырғалары бірдей тӛрт бӛлікке бӛлініп табандарына пареллель кесінділермен қосылған. Егер трапеция табандары 6 м және 18 м болса, осы кесінділер ҧзындықтарын табыңыз
-
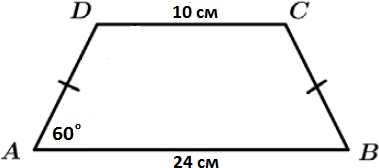
[5 балл] Суретте кӛрсетілген трапеция периметрін табыңыз
-
[4 балл] Тең бҥйірлі ҥшбҧрыштың орта сызығы 11 см болатын табанына параллель. Егер ҥшбҧрыштың периметрі 52 см болса, оның қабырғаларын табыңыз.
- 1 ... 32 33 34 35 36 37 38 39 40
нҧсқа
-
[1 балл] ABCD– ромб берілген. Сбұрышынтабыңыз.
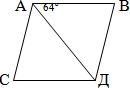 А) 116о Б) 52о В) 64о Г) 128о Д) 32о
А) 116о Б) 52о В) 64о Г) 128о Д) 32о-
[6 балл] ABCD параллелограмының биссектрисасы оның СД қабырғасын СК = 21см және КД = 6 см болатын кесінділерге бӛледі. Оның перимтрін табыңдар.
-
 [4 балл] Трапецияның бҥйр қабырғалары бірдей тӛрт бӛлікке бӛлініп табандарына пареллель кесінділермен қосылған. Егер трапеция табандары 8 м және 24 м болса, осы кесінділер ҧзындықтарын табыңыз.
[4 балл] Трапецияның бҥйр қабырғалары бірдей тӛрт бӛлікке бӛлініп табандарына пареллель кесінділермен қосылған. Егер трапеция табандары 8 м және 24 м болса, осы кесінділер ҧзындықтарын табыңыз.
-
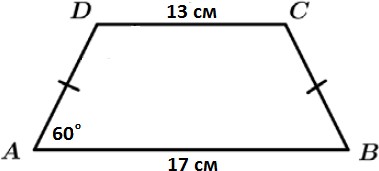
[5 балл] Суретте кӛрсетілген трапеция периметрін табыңыз
-
[4 балл] Тең бҥйірлі ҥшбҧрыштың орта сызығы 7 см болатын табанына параллель. Егер ҥшбҧрыштың периметрі 36 см болса, оның қабырғаларын табыңыз.
Балл қою схемасы
| № | 1 нҧсқа | 2 нҧсқа | балл |
| 1 | в | Б | 1 |
| 2 | Есеп шартына сәйкес суретін салады | Есеп шартына сәйкес суретін салады | 1 |
| ВС қабырғасын табады (ВС = 19+10=29) | ДС қабырғасын табады (ДС = 6+21=27) | 1 | |
| Пареллель тҥзулердің белгілерін қолданады | Пареллель тҥзулердің белгілерін қолданады | 1 | |
| Бҧрыштар теңдігіне қорытынды жасайды ∠ВАК = ∠ДАК (АК - биссектриса) ∠ВКА = ∠ДАК (н\леж) ∠ВАК = ∠ВКА | Бҧрыштар теңдігіне қорытынды жасайды ∠АВК = ∠СВК (ВК - биссектриса) ∠АВК = ∠ВКС (н\леж) ∠СВК = ∠СКВ | 1 | |
| Тең бҥйірлі ҥшбҧрышты анықтайды АВ = ВК = 19 см | Тең бҥйірлі ҥшбҧрышты анықтайды ВС = СК = 27 см | 1 | |
| Р = 2(19 + 29) = 58 | Р = 2(21 + 27) = 96 | 1 | |
| 3 | Фалес теоремасымен қорытынды жасайды | Фалес теоремасымен қорытынды жасайды | 1 |
| (18 + 6) : 2 = 12 | (24 + 8) : 2 = 16 | 1 | |
| (18 + 12) : 2 = 15 | (24 + 16) : 2 = 20 | 1 | |
| (12 + 6) : 2 = 9 | (16 + 8) : 2 = 12 | 1 | |
| 4 | С және Д нҥктелерінен перпендикулярлар тҥсіреді | С және Д нҥктелерінен перпендикулярлар тҥсіреді | 1 |
| Тең бҥйірлі трапеция қасиетін қолданады: (24 – 10) : 2 = 7 | Тең бҥйірлі трапеция қасиетін қолданады : (17 – 13) : 2 = 2 | 1 | |
| Тік бҧрышты ҥшбҧрышты қарастырып, 30о туралы теореманы қолданады | Тік бҧрышты ҥшбҧрышты қарастырып, 30о туралы теореманы қолданады | 1 | |
| АД = ВС = 14 | АД = ВС = 4 | 1 | |
| Р = 24 + 14 + 10 + 14 = 62 | Р = 17 + 4 + 13 + 4 = 38 | 1 | |
| 5 | Есеп шартына сәйкес суретін салады | Есеп шартына сәйкес суретін салады | 1 |
| Ҥшбҧрыштың орта сызығы туралы теореманы қолданады | Ҥшбҧрыштың орта сызығы туралы теореманы қолданады | 1 | |
| Табан қабырғасын табады: 11 ∙ 2 = 22 | Табан қабырғасын табады: 7 ∙ 2 = 14 | 1 | |
| Бҥйір қабырғаларын табады: (52 -22) : 2 = 15 | Бҥйір қабырғаларын табады: (36 -14) : 2 = 11 | 1 | |
| Барлығы | | 20 | |