Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 293
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
E(p) – ошибка слежения, входной сигнал звена с передаточной функцией K(р). Y(p) – выходной сигнал звена K(р), который одновременно является выходным сигналом системы Y(p). Линия, по которой передается входной сигнал системы, называется линией (каналом) прямой связи. Линия, начинающаяся от точки разветвления R и передающая сигнал в обратном направлении, называется линией (каналом) обратной связи. Сумматор, звено K(р) расположены на линии прямой связи. Звено Kос(р) включено в линию обратной связи.
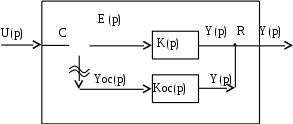
Рис. 4.3. Схема соединения с обратной связью
Система с обратной связью называется замкнутой.
Если сигнал линии обратной связи входит в сумматор со знаком, противоположным знаку задающего сигнала U(p), обратная связь называется отрицательной. Это указывается зачернением соответствующего сектора сумматора или пометкой знаком «минус». Примем, что обратная связь отрицательная, E(p) = U(p) – Yoc(p). (в случае положительной обратной связи E(p) = U(p) + Yoc(p)).
Для замкнутой системы можно составить несколько передаточных функций.
4.2.4. Передаточная функция разомкнутой системы
Получается, если разорвать обратную связь, например возле сумматора, как показано волнистыми черточками на рис. 4.3. В таком случае выходным сигналом оказывается Yoc(p), а передаточная функция будет отношением Yoc(p) к U(p):
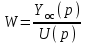. (4.5)
Методом обратного движения осуществим построение операторного уравнения разомкнутой системы (аргумент р опустим):
.
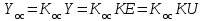То есть, согласно (4.5), передаточной функцией разомкнутой системы будет:
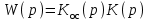. (4.6)
Если вместо звена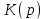
будет группа уже соединенных звеньев с передаточной функцией 
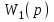, вид формулы остается тем же:
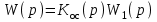. (4.7)
Передаточная функция разомкнутой системы характеризует собственные динамические свойства системы.
4.2.5. Передаточная функция замкнутой системы
Выходным сигналом, как обозначено на схеме рис. 4.3, будет Y(p), входным U(p).
Передаточная функция замкнутой системы – обозначим ее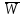
есть отношение изображения регулируемой величины к изображению задающего воздействия:
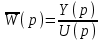. (4.8)
Двигаясь по контуру регулирования против направления передачи сигнала, получаем:
.
.
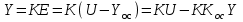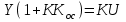По определению (4.8) передаточной функцией замкнутой системы будет:
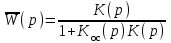. (4.9)
Знак «плюс» в знаменателе соответствует отрицательной обратной связи. В случае положительной обратной связи ставиться знак «минус».
Обратная связь через усилительное звено называется жесткой, через дифференцирующее звено – мягкой.
Если в линии обратной связи звено отсутствует, и выходной сигнал системы непосредственно подается на вход, то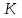
ос(р) = 1. Замкнутая система имеет передаточную функцию
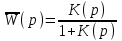. (4.10)
Передаточная функция замкнутой системы характеризует передачу системой задающего воздействия, его воспроизведение регулируемой величиной.
П
ример 4.6.
Разомкнутую систему из последовательно соединенных двух одинаковых инерционных звеньев замыкают. Найти передаточную функцию.
По условию,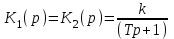
.Значит, передаточная функция разомкнутой системы
.
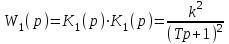Согласно формуле (4.5), передаточная функция замкнутой системы
.
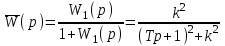П
ример 4.7.
Интегрирующее звено соединяется последовательно с инерционным звеном. Соединение охватывается жесткой отрицательной обратной связью.
Найти передаточную функцию.
Передаточные функции звеньев:
, 
, 
.
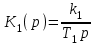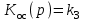Перемножая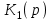
и 
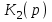, получаем передаточную функцию соединения:
.
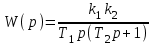Передаточная функция замкнутой системы
.
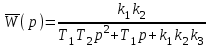Если произведение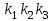
вынести за скобку, обозначить 
, 
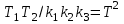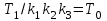и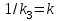 
, проявится структура передаточной функции звена второго порядка:
.
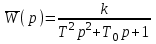То есть, замкнутая система будет вести себя либо как колебательное звено (при условии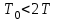
), либо как апериодическое звено (при условии ).
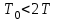П
ример 4.8.
Инерционное звено последовательно соединяется с интегрирующем. К цепочке параллельно подсоединяется звено с единичной передаточной функцией. Вся система охватывается жесткой обратной связью.
Найти передаточную функцию системы.
Структурная схема представлена на рис. 4.4.
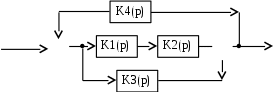
Рис. 4.4. Структурная схема по условиям примера 4.8
Выпишем передаточные функции:
, 
, 
, 
.
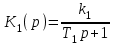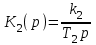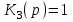Находим передаточную функцию разомкнутой системы из двух звеньев,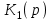 и :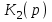
.
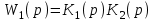Находим передаточную функцию параллельного соединения:
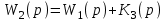
Находим передаточную функцию замкнутой системы с учетом того, что обратная связь положительная:
.
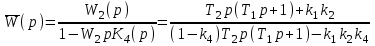Можно убедиться, что результат будет таким же, если нанести на схему обозначения сигналов и применить метод обратного движения.
4.2.6. Передаточная функция по ошибке
Рассмотрим схему замкнутой САР на рис. 4.5. На схеме отдельно обозначены передаточная функция управляющего устройства W1(p) и передаточная функция объекта управления W2(p).
Рис. 4.5. Система, замкнутая отрицательной обратной связью
Определим передаточную функцию по ошибке как отношение изображения ошибки слежения Е(р) к изображению задающего воздействия U(p):
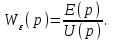(4.11)
Имея ввиду, что выходной величиной «системы» в данном случае будет Е(р), методом обратного движения получаем:
,
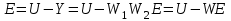где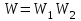
– передаточная функция последовательного соединения звеньев. Она же – передаточная функция разомкнутой системы.
Следовательно,
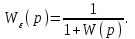(4.12)
Передаточная функция по ошибке обратно пропорциональна передаточной функции разомкнутой системы.
4.2.7. Передаточная функция по возмущению
Пусть система, помимо управляющего воздействия U(p), испытывает возмущающее воздействие Z(р). Дополним схему рис. 4.5. каналом возмущения. Получается система, которая имеет два входных воздействия и одно выходное, рис. 4.6.
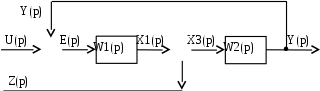
Рис. 4.6. Схема следящей САР под воздействием возмущения
Передаточную функцию по возмущению определим как отношение изображения выходной величины системы Y(p) к изображению входной величины Z(p):
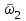. (4.13)
Методом обратного движения получаем:
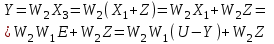
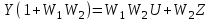. (4.14)
По принципу суперпозиции каждый сигнал проходит через систему независимо от других. Это значит, что для каждого будет своя передаточная функция. По возмущению,
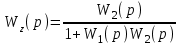(4.15)
и по управлению:
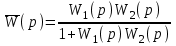
Произведение
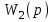представляет собой передаточную функцию разомкнутой системы 
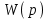. Поэтому формулу (4.15) можно записать в виде
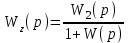. (4.16)
Передаточная функция по возмущению есть отношение передаточной функции объекта управления к передаточной функции разомкнутой системы, увеличенной на единицу.
П
ример 4.9.
В замкнутой системе регулирующее устройство и объект регулирования имеют передаточные функции
, 
.
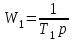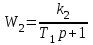Передаточная функция звена канала возмущения равна коэффициенту усиления k3.
Найти передаточную функцию по ошибке и передаточную функцию по возмущению.
В первом случае
.
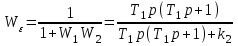Во втором случае
.
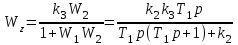4.2.8. Передаточные функции системы
с перекрестными связями
Рассмотрим систему, имеющую два входных сигнала Х1(р) и Х1(р) и два выходных, Y1(р) и Y2(р). Каждый из входных сигналов влияет на оба выходных. Структурная схема системы показана на рис. 4.7.
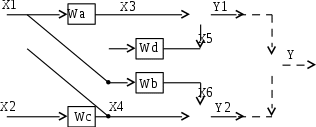
Рис. 4.7. Структурная схема системы с перекрестными связями
Методом обратного движения устанавливаем:
,
.
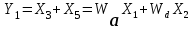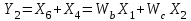Полученные уравнения показывают, по какому закону формируются выходные величины.
Рис. 4.3. Схема соединения с обратной связью
Система с обратной связью называется замкнутой.
Если сигнал линии обратной связи входит в сумматор со знаком, противоположным знаку задающего сигнала U(p), обратная связь называется отрицательной. Это указывается зачернением соответствующего сектора сумматора или пометкой знаком «минус». Примем, что обратная связь отрицательная, E(p) = U(p) – Yoc(p). (в случае положительной обратной связи E(p) = U(p) + Yoc(p)).
Для замкнутой системы можно составить несколько передаточных функций.
4.2.4. Передаточная функция разомкнутой системы
Получается, если разорвать обратную связь, например возле сумматора, как показано волнистыми черточками на рис. 4.3. В таком случае выходным сигналом оказывается Yoc(p), а передаточная функция будет отношением Yoc(p) к U(p):
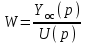. (4.5)Методом обратного движения осуществим построение операторного уравнения разомкнутой системы (аргумент р опустим):
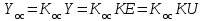.То есть, согласно (4.5), передаточной функцией разомкнутой системы будет:
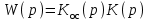. (4.6)Если вместо звена
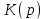будет группа уже соединенных звеньев с передаточной функцией 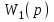, вид формулы остается тем же: 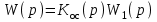. (4.7)Передаточная функция разомкнутой системы характеризует собственные динамические свойства системы.
4.2.5. Передаточная функция замкнутой системы
Выходным сигналом, как обозначено на схеме рис. 4.3, будет Y(p), входным U(p).
Передаточная функция замкнутой системы – обозначим ее
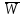есть отношение изображения регулируемой величины к изображению задающего воздействия: 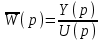. (4.8)Двигаясь по контуру регулирования против направления передачи сигнала, получаем:
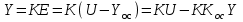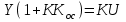. .По определению (4.8) передаточной функцией замкнутой системы будет:
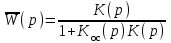. (4.9)Знак «плюс» в знаменателе соответствует отрицательной обратной связи. В случае положительной обратной связи ставиться знак «минус».
Обратная связь через усилительное звено называется жесткой, через дифференцирующее звено – мягкой.
Если в линии обратной связи звено отсутствует, и выходной сигнал системы непосредственно подается на вход, то
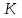ос(р) = 1. Замкнутая система имеет передаточную функцию 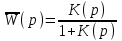. (4.10)Передаточная функция замкнутой системы характеризует передачу системой задающего воздействия, его воспроизведение регулируемой величиной.
П
ример 4.6.
Разомкнутую систему из последовательно соединенных двух одинаковых инерционных звеньев замыкают. Найти передаточную функцию.
По условию,
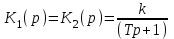.Значит, передаточная функция разомкнутой системы 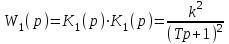.Согласно формуле (4.5), передаточная функция замкнутой системы
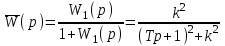.П
ример 4.7.
Интегрирующее звено соединяется последовательно с инерционным звеном. Соединение охватывается жесткой отрицательной обратной связью.
Найти передаточную функцию.
Передаточные функции звеньев:
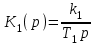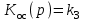, , .Перемножая
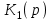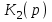и , получаем передаточную функцию соединения: 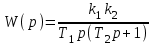.Передаточная функция замкнутой системы
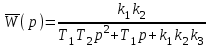.Если произведение
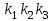вынести за скобку, обозначить 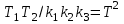, 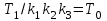и 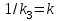, проявится структура передаточной функции звена второго порядка: 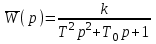.То есть, замкнутая система будет вести себя либо как колебательное звено (при условии
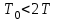), либо как апериодическое звено (при условии 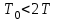).П
ример 4.8.
Инерционное звено последовательно соединяется с интегрирующем. К цепочке параллельно подсоединяется звено с единичной передаточной функцией. Вся система охватывается жесткой обратной связью.
Найти передаточную функцию системы.
Структурная схема представлена на рис. 4.4.
Рис. 4.4. Структурная схема по условиям примера 4.8
Выпишем передаточные функции:
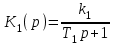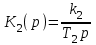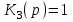, , , .Находим передаточную функцию разомкнутой системы из двух звеньев,
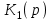и 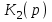: 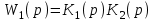.Находим передаточную функцию параллельного соединения:
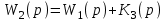
Находим передаточную функцию замкнутой системы с учетом того, что обратная связь положительная:
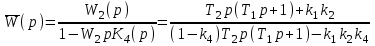.Можно убедиться, что результат будет таким же, если нанести на схему обозначения сигналов и применить метод обратного движения.
4.2.6. Передаточная функция по ошибке
Рассмотрим схему замкнутой САР на рис. 4.5. На схеме отдельно обозначены передаточная функция управляющего устройства W1(p) и передаточная функция объекта управления W2(p).
Рис. 4.5. Система, замкнутая отрицательной обратной связью
Определим передаточную функцию по ошибке как отношение изображения ошибки слежения Е(р) к изображению задающего воздействия U(p):
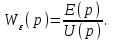(4.11)Имея ввиду, что выходной величиной «системы» в данном случае будет Е(р), методом обратного движения получаем:
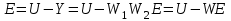,где
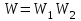– передаточная функция последовательного соединения звеньев. Она же – передаточная функция разомкнутой системы.Следовательно,
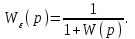(4.12)Передаточная функция по ошибке обратно пропорциональна передаточной функции разомкнутой системы.
4.2.7. Передаточная функция по возмущению
Пусть система, помимо управляющего воздействия U(p), испытывает возмущающее воздействие Z(р). Дополним схему рис. 4.5. каналом возмущения. Получается система, которая имеет два входных воздействия и одно выходное, рис. 4.6.
Рис. 4.6. Схема следящей САР под воздействием возмущения
Передаточную функцию по возмущению определим как отношение изображения выходной величины системы Y(p) к изображению входной величины Z(p):
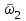. (4.13)Методом обратного движения получаем:
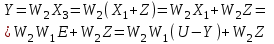
Откуда
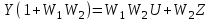. (4.14)По принципу суперпозиции каждый сигнал проходит через систему независимо от других. Это значит, что для каждого будет своя передаточная функция. По возмущению,
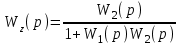(4.15)и по управлению:
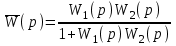
Произведение
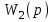представляет собой передаточную функцию разомкнутой системы 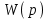. Поэтому формулу (4.15) можно записать в виде 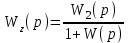. (4.16)Передаточная функция по возмущению есть отношение передаточной функции объекта управления к передаточной функции разомкнутой системы, увеличенной на единицу.
П
ример 4.9.
В замкнутой системе регулирующее устройство и объект регулирования имеют передаточные функции
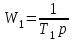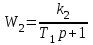, .Передаточная функция звена канала возмущения равна коэффициенту усиления k3.
Найти передаточную функцию по ошибке и передаточную функцию по возмущению.
В первом случае
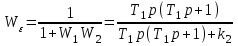.Во втором случае
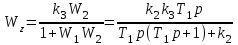.4.2.8. Передаточные функции системы
с перекрестными связями
Рассмотрим систему, имеющую два входных сигнала Х1(р) и Х1(р) и два выходных, Y1(р) и Y2(р). Каждый из входных сигналов влияет на оба выходных. Структурная схема системы показана на рис. 4.7.
Рис. 4.7. Структурная схема системы с перекрестными связями
Методом обратного движения устанавливаем:
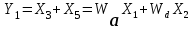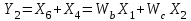, .Полученные уравнения показывают, по какому закону формируются выходные величины.