ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 473
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Общее решение данной задачи получается в связи с этим в виде:
![]() при
при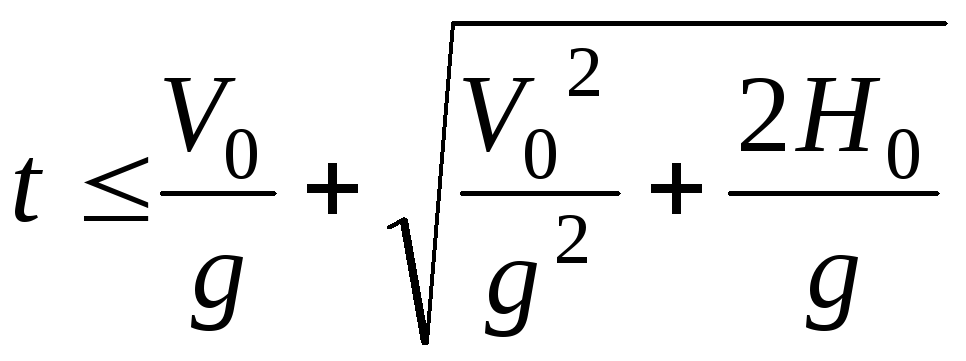 и
и
![]() при
при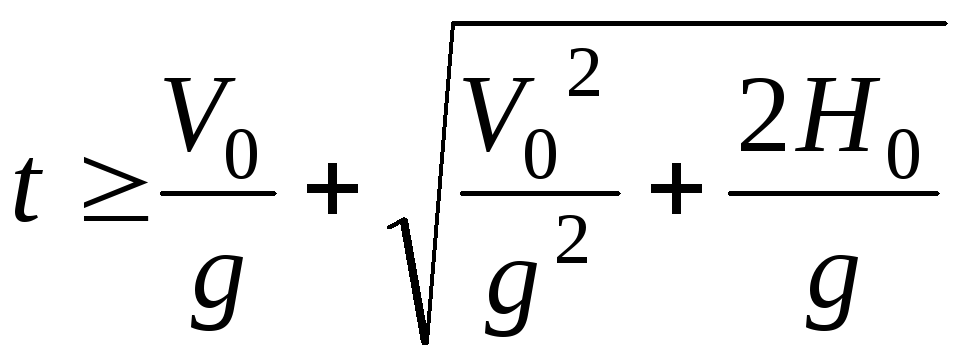 .
.
Вычисляем искомые значения координат:
y(0,5) = 20 + 50,5 - 50,25 = 21,5 (м) – выше первоначального положения,
y(1) = 20 + 51 - 51 = 20 (м) – на той же высоте, что и в начале,
y(2) = 20 + 52 - 54 = 10 (м) – ниже начального положения,
y(10) = 0 (м) – на поверхности земли.
Задача-пример 4.На горизонтальном валу, совершающем 200 об/с, на расстоянии 20 см друг от друга закреплены два тонких диска. Для определения скорости полета пули произведен выстрел так, что пуля пробила оба диска на одинаковом расстоянии от оси вращения. Определить скорость пули, если угловое смещение пробоин оказалось равным 180.
Р
Дано: n= 200об/с d=0,2 м 10= 180
V- ? ешение:
В данной задаче рассматриваются разные
тела с различными видами движения.
ешение:
В данной задаче рассматриваются разные
тела с различными видами движения.
Т ак,
рассматривая вращательное движение
пробоин, получим закон вращения:
ак,
рассматривая вращательное движение
пробоин, получим закон вращения:![]() ,
где
,
где![]() .
Подставим:
.
Подставим:![]() - общая формула зависимости угла поворота
пробоин за времяt.
- общая формула зависимости угла поворота
пробоин за времяt.
С другой стороны, рассматривая равномерное
движение пули, получим для нее закон
движения:
![]() - общая формула зависимости пройденного
расстояния от времени движения пули
(форма 1).
- общая формула зависимости пройденного
расстояния от времени движения пули
(форма 1).
На основе полученных общих формул
запишем теперь конкретные равенства с
учетом данных задачи. Для этого обозначим
через t1– время полета пули между двумя дисками.
Тогда за времяt1пуля пройдет расстояниеd,
а вторая пробоина повернется на угол![]() ,
т.е.:
,
т.е.:
![]() и
и![]() .
.
Делим второе на первое и выражаем искомую величину скорости пули:
![]()
![]() .
Итак, получено решение в общем виде.
Но…! Обращаем внимание на требование
соблюдение единой размерности однородных
величин. В дано записано значение угла
поворота в градусах, в то время как все
готовые формулы, которые мы использовали
при решении предполагают, что угловые
величины измеряются в радианах! Поэтому
необходимо в общую формулу решения
включить параметры перевода градусов
в радианы. Проще всего осуществлять
переход по пропорции:
.
Итак, получено решение в общем виде.
Но…! Обращаем внимание на требование
соблюдение единой размерности однородных
величин. В дано записано значение угла
поворота в градусах, в то время как все
готовые формулы, которые мы использовали
при решении предполагают, что угловые
величины измеряются в радианах! Поэтому
необходимо в общую формулу решения
включить параметры перевода градусов
в радианы. Проще всего осуществлять
переход по пропорции:
![]() радиан --- 3600
радиан --- 3600
![]() радиан ---
радиан ---![]() 0.
Отсюда
0.
Отсюда![]() ,
тогда получаем:
,
тогда получаем:
![]() ,
т.е. окончательно имеем:
,
т.е. окончательно имеем:
![]() .
.
Вычислим:
![]() (м/с).
(м/с).
Ответ: скорость пули равна 800 м/с
Задача-пример 5.Вслед движущемуся со скоростью 7 м/с грузовику бросили мяч со скоростью 15 м/с. С какой скоростью мяч отлетит от кузова грузовика, если удар считать абсолютно упругим.
Р
Дано: V1
= 7 м/с V2
= 15 м/с
V3
- ?
 ешение:
Делаем рисунок (рис. а), на котором
указываем направления скоростей тел,
рассматриваемых в данной задаче.
ешение:
Делаем рисунок (рис. а), на котором
указываем направления скоростей тел,
рассматриваемых в данной задаче.
Анализируя условие задачи, замечаем,
что мяч (Т) движется относительно двух
систем отсчета: земля (К) и грузовик
(К’), причем V1– переносная скорость (![]() ),
аV2– абсолютная скорость мяча (
),
аV2– абсолютная скорость мяча (![]() - относительно К, т.е. Земли). Причем
спрашивается в задаче опять же про
скорость относительно земли, в то время
как сам удар происходит в системе отсчета
К’.
- относительно К, т.е. Земли). Причем
спрашивается в задаче опять же про
скорость относительно земли, в то время
как сам удар происходит в системе отсчета
К’.
Поэтому все решение представим в три этапа:
1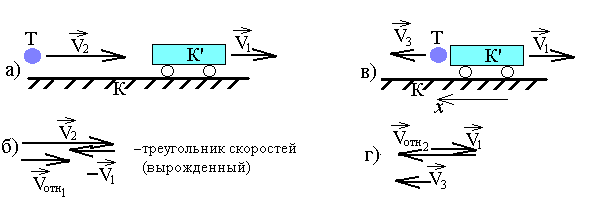 этап.Переходим к новой системе
отсчета К’, т.е. найдем из формулы
сложения скоростей (15) относительную
скорость мяча:
этап.Переходим к новой системе
отсчета К’, т.е. найдем из формулы
сложения скоростей (15) относительную
скорость мяча:![]()
или, в наших обозначениях:
![]() .
Далее строим на основе векторного
равенства треугольник скоростей (рис.
б), из которого находим нужное числовое
значение:Vотн2
= V2
– V1
=15 – 7 = 8 (м/с). С такой скоростью
мяч подлетает к грузовику.Это
промежуточное вычисление можно не
делать.
.
Далее строим на основе векторного
равенства треугольник скоростей (рис.
б), из которого находим нужное числовое
значение:Vотн2
= V2
– V1
=15 – 7 = 8 (м/с). С такой скоростью
мяч подлетает к грузовику.Это
промежуточное вычисление можно не
делать.
2 этап.Рассматривая абсолютно упругий удар
мяча о грузовик заключаем, что мяч
отлетит от кузова со скоростью, равной
по величине и противоположной по
направлению по отношению к![]() :
:![]() .
.
Причем все это в системе К’.
3 этап.Переходим обратно в систему отсчета К.
Считая, что величина скорости грузовика
не меняется в результате удара, делаем
новый рисунок с указанием скоростей
тел уже после удара (рис. в). Применяем
опять формулу (15):![]() .Строим
по ней треугольник скоростей (рис. г) и
получаем окончательно значение искомой
величины:
.Строим
по ней треугольник скоростей (рис. г) и
получаем окончательно значение искомой
величины:
![]() .
.
Как видим, формула общего решения имеет векторный вид. Для нахождения числового значения искомой величины выбираем на рисунке направление оси хи проектируем последнее равенство на нее:V3x = 2(-V1) – (-V2) = V2 – 2V1. Вычисляем:V3x = 15 - 27 = 1 (м/с).
Замечание. В случае, когда V2 2V1, мяч после удара о кузов будет двигаться в прежнем направлении (т.е. вслед грузовику), но с меньшей скоростью.
Ответ: 1 м/с.
ЗАДАЧИ к разделу «Кинематика»
Прямолинейное движение
За 4 с движения тело прошло путь 40 м. Какой путь тело пройдет за 8 с от начала отсчета времени, если начальная скорость равна 5 м/с. [120 м]
Тело, выведенное из состояния покоя, двигаясь равноускоренно, прошло 200 мза 10с. Какое расстояние прошло тело за 2сот начала движения?
Материальная точка движется с ускорением а. Определить разность путей, проходимых точкой в два последовательных одинаковых промежутка времениt.
При равноускоренном движении точка проходит в первые два равных промежутка времени по t= 4 с каждый путиS1= 24 м иS2=64 м. Определить ускорение и начальную скорость.
Тело переместилось из точки А(-1;2) в точку В(5;3). Сделайте чертеж, найдите перемещение тела и его проекции на оси координат.
Известно, что траектории двух материальных точек пересекаются. Столкнутся ли эти точки? Каково условие столкновения (встречи) двух точек?
Движение грузового автомобиля описывается уравнением х=-270+12t. Опишите характер движения автомобиля. Найдите начальную координату, модуль и направление вектора скорости, координату и перемещение автомобиля за 20 с. Когда автомобиль пройдет через начало координат? Постройте график зависимостих(t)иvx(t).
Движение двух велосипедистов описывается уравнениями х1=12tих2=120-10t. Опишите характер движения каждого велосипедиста, найдите модуль и направление их скоростей, постройте графики движения, графики скорости, и определите графически и аналитически время и место встречи этих велосипедистов.
За одно и тоже время 2 автомобиля прошли одинаковый путь. Первый автомобиль двигался с ускорением а с нулевой начальной скоростью. Второй – первую половину пути двигался со скоростьюv1, а вторую половину – со скоростьюv2. Найти путь, пройденный каждым автомобилем.
Двигаясь равноускоренно, велосипедист за время t1увеличил свою скорость от значенияv1доv2. Затем в течение времени t2он двигался равномерно. Найти путь, пройденный велосипедистом за все время движения.
*Автобус движется в течение 20 спо прямой до остановки, проходя при этом расстояние 310м. Его начальная скорость 15м/с. Докажите, что ускорение автобуса меняется по направлению.
Два автомобиля выходят из одного пункта в одном направлении. Второй автомобиль выходит на 0,5 мин позже первого. Оба движутся с одинаковым ускорением 0,4 м/с2. Через сколько времени, считая от начала движения первого автомобиля, расстояние между ними окажется 540 м?
Тело, имея начальную скорость V0 = 1 м/с, двигалось равноускоренно и приобрело, пройдя некоторое расстояние, скорость V = 7 м/с. Найти скорость на половине этого расстояния.[5 м/с]
Автомобиль начинает двигаться и первую часть пути проходит равноускоренно за время t1, а вторую равнозамедленно до полной остановки. Весь путь длинойlавтомобиль проходит за времяt. Определить его ускорениеа1на первой части пути.
На пути 60 м скорость тела уменьшилась в три раза за 20 с. Определить скорость тела в конце пути, считая ускорение постоянным. [1,5 м/с]
Скорость тела на пути 106,25 м увеличилась на 5 м/с. Определить ускорение тела, если скорость в начале пути равна 6 м/с. [0,4 м/с2]
*В момент, когда опоздавший пассажир вбежал на платформу, мимо него прошел за время t1предпоследний вагон. Последний вагон прошел мимо пассажира за времяt2. На сколько опоздал пассажир к поезду (t0)? Поезд движется равноускоренно. Длина вагонов одинакова.
*По наклонной доске пустили катиться снизу вверх шарик. На расстоянии l= 30 см от начала пути шарик побывал дважды: черезt1= 1 с и черезt2= 2 с после начала движения. Определить начальную скорость и ускорение движения шарика, считая его постоянным.