ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 468
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
ЗАДАЧИ к разделу «Статика»
Светофор массой 4 кг подвешен над дорогой на двух одинаковых тросах, угол между которыми составляет 1200. Считая тросы невесомыми, найти их натяжение. Ускорение свободного падения принять равным 9,8 м/с2.
Полый шарик из алюминия ( = 2700 кг/м3) в воде (1 = 1000 кг/м3) имеет весР1= 0,24 Н, а в бензине (2 = 700 кг/м3)Р2= 0, 33 Н. Найти объемV1полости.
Труба длиной 5 м и массой 40 кг лежит горизонтально на двух опорах. Одна из опор расположена на расстоянии 1 м от правого конца трубы. Какую минимальную силу нужно приложить к левому концу трубы, чтобы ее приподнять?
Лом весом 160 Н и длиной 2 м лежит на ящике шириной 1 м, выступая на края его на 0,4 м и 0,6 м. Какую минимальную силу нужно приложить к лому, чтобы приподнять длинный его конец? [60 Н]
На какую минимальную высоту может приподняться человек по невесомой лестнице, имеющей длину lи приставленную к гладкой стенке? Угол между лестницей и стенкой, коэффициент трения о пол. [
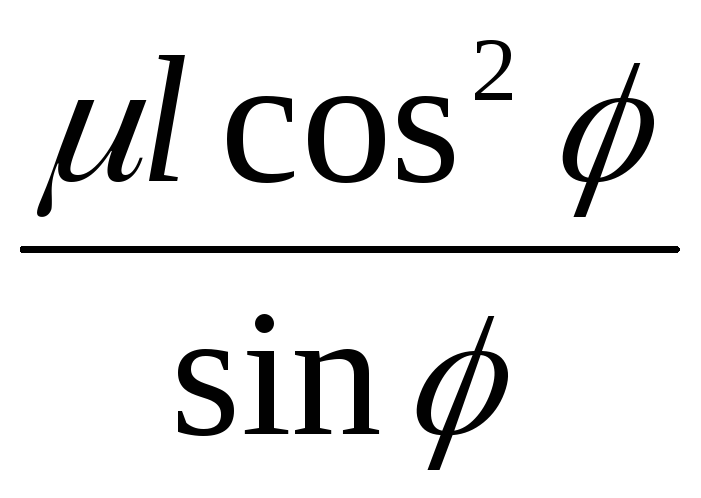 ]
]О
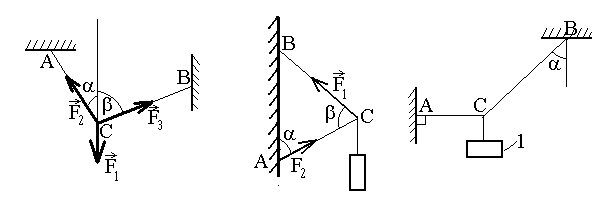 пределить
модуль силы
пределить
модуль силы натяжения троса ВС, если известно, что
натяжение троса АС равноF2= 15 Н. В положении равновесия углы
= 300и
= 750.
натяжения троса ВС, если известно, что
натяжение троса АС равноF2= 15 Н. В положении равновесия углы
= 300и
= 750.Шарнирный трехзвенник АВС удерживает в равновесии груз, подвешенный к шарнирному болту С. Под действием груза стержень АС сжат силой F2 = 25 Н. Заданы углы = 600и = 450. Считая стержни АС и ВС невесомыми, определить усилие в стержне ВС.
Груз 1 весом 2 Н удерживается в равновесии двумя веревками АС и ВС, расположенными в вертикальной плоскости. Определить натяжение веревки ВС, если угол = 300.
Кусок сплава меди и серебра весит в воздухе 2,940 Н, а в воде – 2,646 Н. Сколько серебра и меди в куске, выразить в граммах. [0,083 г и 0,217 г]
Сплошной однородный шар плавает на границе раздела двух несмешивающихся жидкостей, плотности которых равны 800 кг/м3и 1000 кг/м3. Определить плотность тела, если в верхней жидкости находится 30% всего объема шара. [940 кг/м3]
Тело кубической формы плавает на поверхности ртути, причем в ртути находится 0,6 всего объема тела. Какая часть тела будет погружена в ртуть, если поверх нее налить слой жидкости, закрывающей тело, плотность которой 3600 кг/м3. Плотность ртути 13 600 кг/м3. [0,456]
Дубовый шар массой 0,6 кг лежит на дне сосуда, наполовину погруженный в воду. Определить силу давления шара на дно сосуда. Плотность дуба 800 кг/м3, воды 1000 кг/м3. Принятьg = 10 м/с2. [2,25 Н]
Часть четвертая:Работа силы. Механическая энергия и количество теплоты. Импульс. Законы изменения и сохранения импульса и полной механической энергии.
Основные понятия и законы
Пусть на тело действует сила
![]() и за некоторое времяtоно переместилось на вектор
и за некоторое времяtоно переместилось на вектор![]() .
Физическая величина, равная скалярному
произведению вектора силы на вектор
соответствующего перемещения, называется
работой этой силы по перемещению тела:
.
Физическая величина, равная скалярному
произведению вектора силы на вектор
соответствующего перемещения, называется
работой этой силы по перемещению тела:
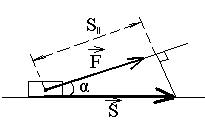
![]() = FScos
= FS
(4.1),
= FScos
= FS
(4.1),
[A] = Дж = Нм.
Здесь - угол между векторами силы и перемещения (рис.). ПроизведениеScosсоответствует величине перемещения вдоль направления действия силы, т.е. равна одной из составляющих вектора перемещения. Другая составляющая перпендикулярна действующей силе, а потому эта сила на таком перемещении работы не совершает:
![]() =
=![]() (
(![]() +
+![]() )
=
)
=![]()
![]() +
+![]()
![]() =FS+ 0 =FS
.
=FS+ 0 =FS
.
Выделим несколько случаев, в которых работа не совершается или равна нулю: 1) тело перемещается, но нет действующей на него при этом силы (движение по инерции), т.е. S 0, F = 0;
сила действует, но тело не перемещается, т.е. F 0, S = 0;
сила действует перпендикулярно перемещению тела, т.е. F 0, S 0, но угол = 900.
В качестве примера случая 3) полезно запомнить следующее. Пусть имеется шарик, закрепленный на вертикальной нити и движущийся по окружности (в вертикальной – рис.а)или горизонтальной –рис.б)плоскости). Здесь сила (или ее проекция) направлена вдоль радиуса окружности, а элементарное перемещение к любой момент времени по отрезку касательной, т.е. они взаимноперпендикулярны и сила натяжения нити не совершает работы. Умение определять работу силы важно еще и потому, что от наличия или отсутствия работы внешних сил зависит будет ли изменяться механическая энергия тела или нет. Также сила реакции опоры в любой момент времени перпендикулярна опоре, по которой движется тело, и ее работа в таких условиях равна нулю всегда!
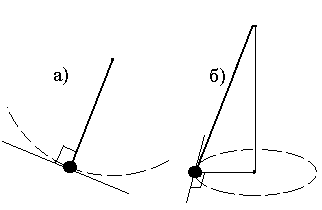
Замечание. Рассмотрим контрпример: человек, сидя на гладком сиденье автобуса, перемещается вместе с последним. Требуется ответить на вопрос: совершает ли в этом случае сила реакции (вертикальной) спинки сиденья работу по перемещению человека в горизонтальном направлении? …
Однозначного ответа нет. Т.е. 1) если автобус движется равномерно, то указанная работа равна нулю (ответ НЕТ), как в первом случае равенства работы силы нулю – движение по инерции (см. выше), 2) при ускоренномдвижении автобуса имеем положительный ответ (ДА).
И еще один момент: если сила и перемещение
противоположно направлены, то угол
= 1800и работа силы будет
отрицательна. Т.е. работа может быть как
положительной величиной, так и
отрицательной, а потому потеря знака
при ее определении будет считаться в
ряде случаев серьезной ошибкой, особенно
если речь идет о суммарной работе
нескольких сил. Кроме того, важно
различать понятия «работа силы![]() »
(обозначим А) и «работа по преодолению
силы
»
(обозначим А) и «работа по преодолению
силы![]() »
(обозначим А), их
связь выражается следующей формулой:
»
(обозначим А), их
связь выражается следующей формулой:
А = А(4.2).
Дальнейшее применение этой формулы будет значительно расширено при рассмотрении работы газов в термодинамике.
Методические
указания. Формула
(4.1) применима лишь в том случае, когда
сила постоянна по величине и по
направлению. В противном случае
аналогичную формулу записываем для
элементарной работы и интегрируем:
![]() ,
где угол
,
где угол![]() тоже может быть функцией перемещения,
т.е. различен в разных участках перемещения
тела.
тоже может быть функцией перемещения,
т.е. различен в разных участках перемещения
тела.
Понятие «энергия» – одно из фундаментальных понятий физики. Энергия – мера движения материи (с позиции философии имеются в виду различные формы движения материи). Энергия - однозначная функция состояния системы, т.е. «любому переходу материальной системы из одного состояния в другое всегда соответствует строго определенное изменение энергиии»[Эвенчик Э.Е. Преподавание механики в курсе физики средней школы. Пособие для учителей. Изд. 2-е, переработ. и доп. - М.: Просвещение, 1971. – 160 с. – С. 134]. Энергия – это общая числовая характеристика конкретных физических форм движения материи: механической, тепловой, электрической и т.д., остающаяся в изолированной системе неизменной величиной при любых их взаимных превращениях.
В связи с этим, работа силы равна величине энергии, переданной от одного тела к другому, или превращенной из одной формы в другую, т.е. служит мерой преобразования энергии.
Замечание. В данном пособии мы рассматриваем лишь механическую работу и механические виды энергии.
Кинетическая энергия(тела) – энергия (его) движения:
![]() (4.3).
(4.3).
Из формулы-определения следует, что кинетическая энергия тела всегда–неотрицательная скалярнаявеличина. Величина этой энергии для данного тела зависит только от его скорости, поэтому, учитывая относительность движения, можно получать различные результаты в разных ИСО.
Прежде чем говорить о потенциальной энергии, уместно вспомнить, что силы бывают потенциальные (консервативные) и непотенциальные (диссипативные).
Основные свойства потенциальных сил: работа силы зависит только от начального и конечного положения тела (иначе говоря, работа не зависит от формы траектории), работа по замкнутому контуру равна нулю; сила однозначно определяется скалярной функцией координат (потенциалом поля, обеспечивающего данный вид взаимодействия).
Потенциальная энергия– энергиявзаимодействия; скалярная величина (может быть отрицательной величиной). Потенциальная энергиясистемы телопределяется их взаимным расположением и характером сил взаимодействия между ними.
Расчетная формула зависит от вида взаимодействия:
гравитационное:
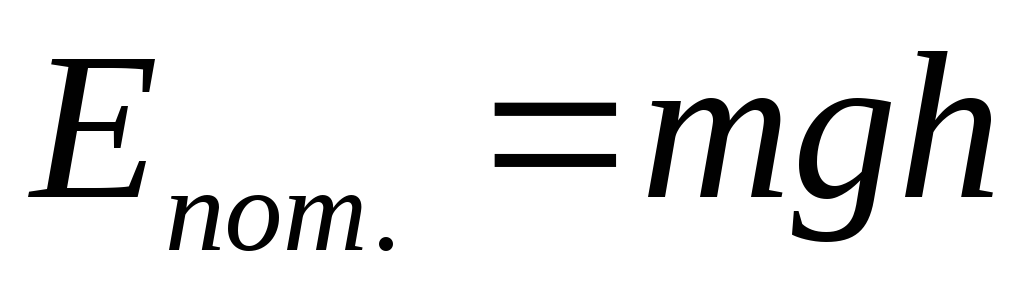 (4.4), где
(4.4), где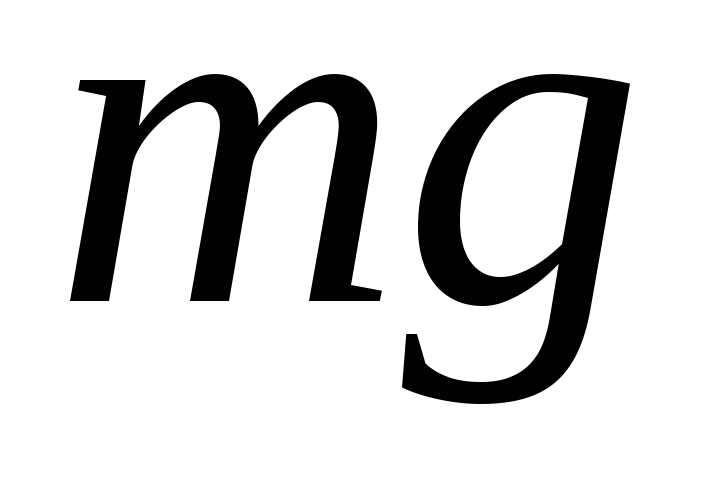 -
сила тяжести, действующая на тело,
-
сила тяжести, действующая на тело,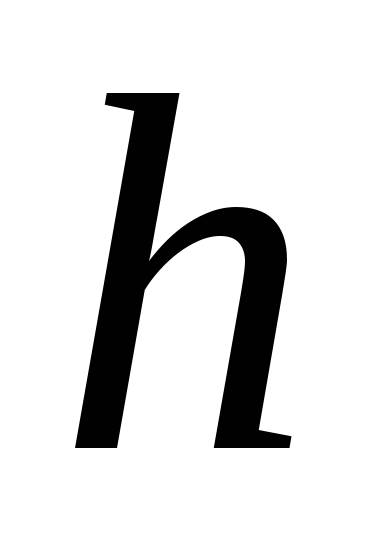 -
высота тела относительно выбранного
нулевого уровня отсчета потенциальной
энергии;
-
высота тела относительно выбранного
нулевого уровня отсчета потенциальной
энергии;упругое:
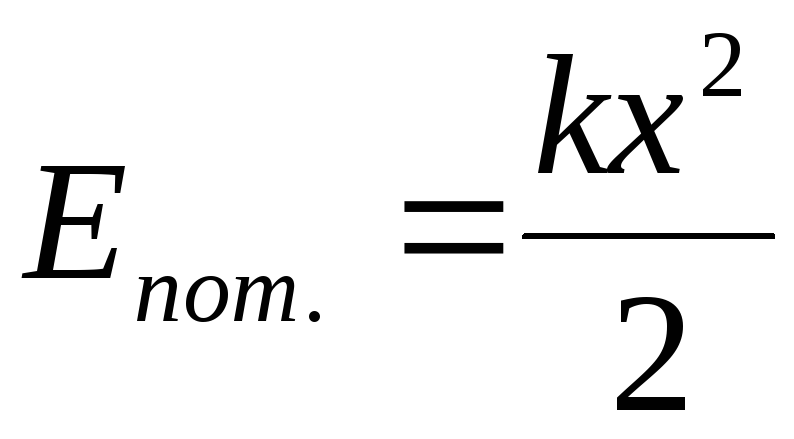 (4.5) - потенциальная энергия сжатой или
растянутой пружины (
(4.5) - потенциальная энергия сжатой или
растянутой пружины (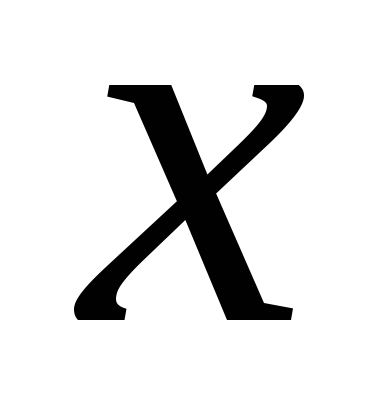 -
величина деформации пружины с
коэффициентом упругости
-
величина деформации пружины с
коэффициентом упругости ).
За нулевой уровень принято положение
недеформированного состояния;
).
За нулевой уровень принято положение
недеформированного состояния;электростатическое:
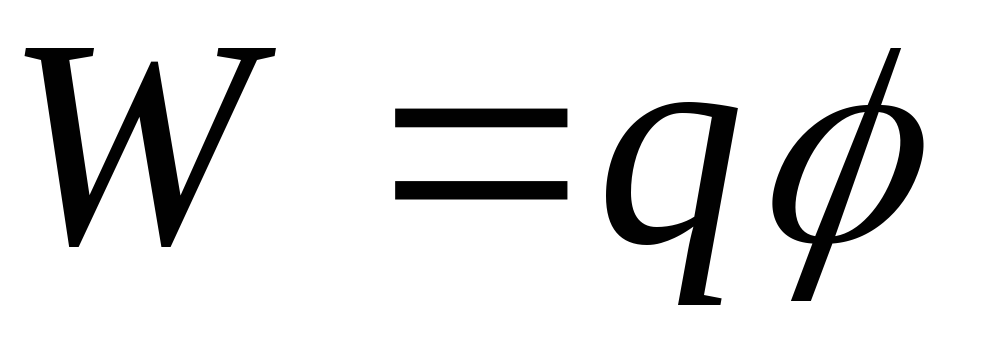 (4.6) - потенциальная энергия заряда
(4.6) - потенциальная энергия заряда ,
находящегося в точке поля с потенциалом
,
находящегося в точке поля с потенциалом .
Если поле создано другим точечным
зарядом Q, то за нулевой уровень отсчета
потенциала часто принимают точку,
находящуюся от Q на расстоянии, равном
бесконечности (где поле отсутствует).
.
Если поле создано другим точечным
зарядом Q, то за нулевой уровень отсчета
потенциала часто принимают точку,
находящуюся от Q на расстоянии, равном
бесконечности (где поле отсутствует).