ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 487
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Дополните предложения САМи.
Ф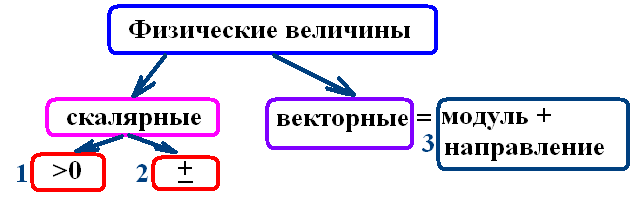 изический
закон раскрывает связь (отношение) между
физическими сторонами проявлений
природных объектов. Эта связь может
быть различного характера, но часто ее
удается сформулировать в соответствии
со схемой:
изический
закон раскрывает связь (отношение) между
физическими сторонами проявлений
природных объектов. Эта связь может
быть различного характера, но часто ее
удается сформулировать в соответствии
со схемой:
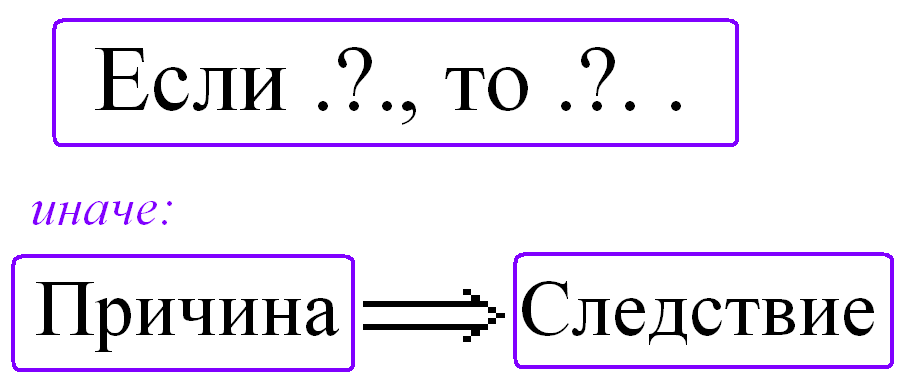
Важно: причина не зависит от следствия!!! Она не может быть найдена через следствие (зная следствие мы не может точно сказать о том, какая причина его вызвала. Можно лишь что-то предположить!). Еще: причина во времени всегда имеет место раньшеследствия: сначала причина, а потом уже следствие.
Причиной изменений являются взаимодействия, а скорость передачи взаимодействия всегда конечна и на его передачу требуется затрата времени.
Физические теории описывают определенный срез физической реальности в определенной интерпретации. Каждая из них включает в себя совокупность фактов (данных экспериментов), специальную терминологию, свод принципов (в том числе методологических) и законов; установление связей между этими компонентами осуществляется на единой основе, характерной для данной теории.
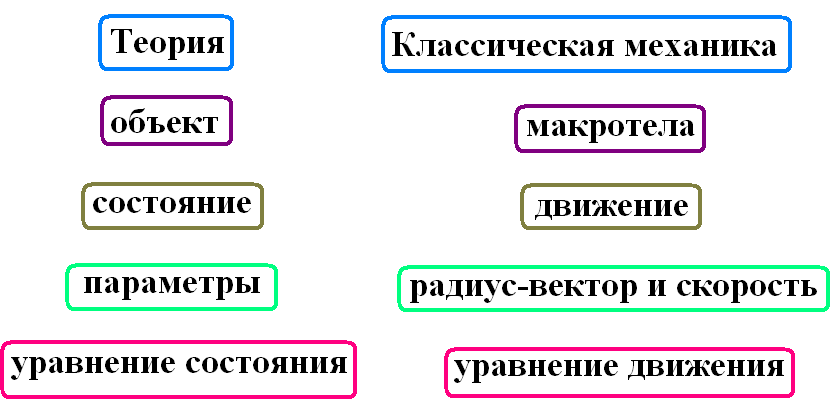
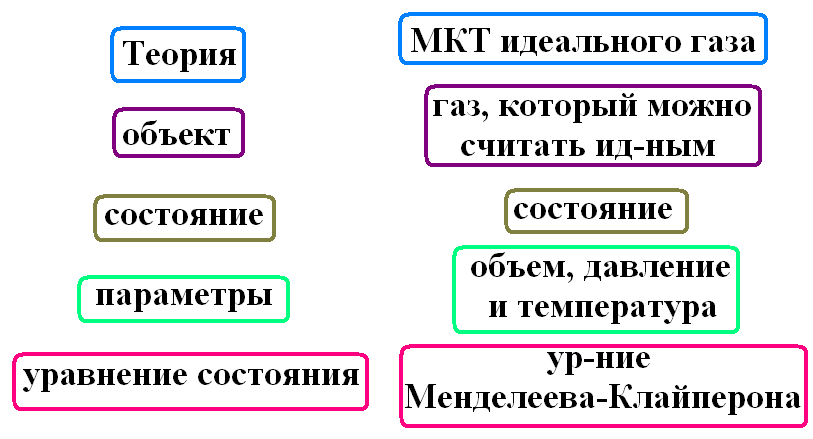
Еще одно сравнение:
План изучения явлений
Внешние признаки явления – признаки, по которым явление обнаруживается.
Условия, при которых оно протекает.
Сущность явления, механизм его протекания (объяснение явления на основании современных научных теорий).
Связь данного явления с другими.
Количественные характеристики явления.
Использование явления на практике.
Способы предупреждения вредного воздействия явления на человека и окружающую вреду.
План изучения физических величин
Какое явление или свойство тел (веществ) характеризует данная величина?
Опредение величины.
Специфические свойства этой величины. Какая эта величина: основная или производная, векторная или скалярная?
Определительная формула (для производной величины).
Единица величины.
Способы измерения величины.
План изучения физических законов
Связь между какими явлениями или величинами выражает данный закон?
Формулировка закона.
Математическое выражение закона.
Опыты, подтверждающие справедливость закона.
Границы применения закона.
Использование закона в практике.
Элементы математики
(производная, вектора и операции над ними).
Из математики необходимо усвоить понятие функциональной зависимости. На примере функции одной переменной
![]() (1)
(1)
это означает, что каждому значению независимой переменной х(из области допустимых значений)соответствует определенное формулой зависимости (1) значение переменнойу.
ПОДУМАЙ: Что значит «переменная»?
Ответ: ……….. (найти в математике и запиши).
Соответствие
Изменение
Зависимость
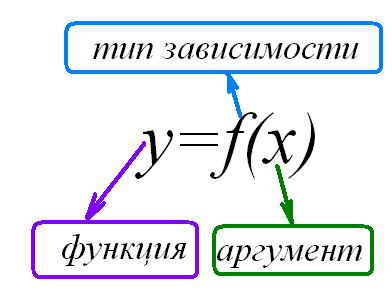
Функция: соответствие, изменение, зависимость.
При разных зависимостях
![]() ,
например
,
например![]() или
или![]() будет иметь место и различное изменение
функции при ОДНОМ и том же изменении
аргумента.
будет иметь место и различное изменение
функции при ОДНОМ и том же изменении
аргумента.
То, насколько и как (уменьшается или увеличивается) меняется функция (зависимая переменная) при единичном изменении аргумента характеризуется ПРОИЗВОДНОЙ от этой функции по этому аргументу.
Производная – от слова произведена от… То есть она получается из функции по определенным правилам и связана с функцией. У каждой функции своя производная. Производная данной функции – тоже есть функция. Отсюда можно говорить о значении производной в данной точке. Чем больше значение производной, тем быстрее меняется функция в этой точке.
Отсюда смысл производной:
Механический: производная – скорость изменения функции.
Геометрический: основан на графическом изображении типа зависимости (тангенс угла наклона касательной к графику функции в данной точке).
В физике переменные могут быть не только скалярами, но и векторами. Поэтому важно уметь осуществлять основные операции над ними.
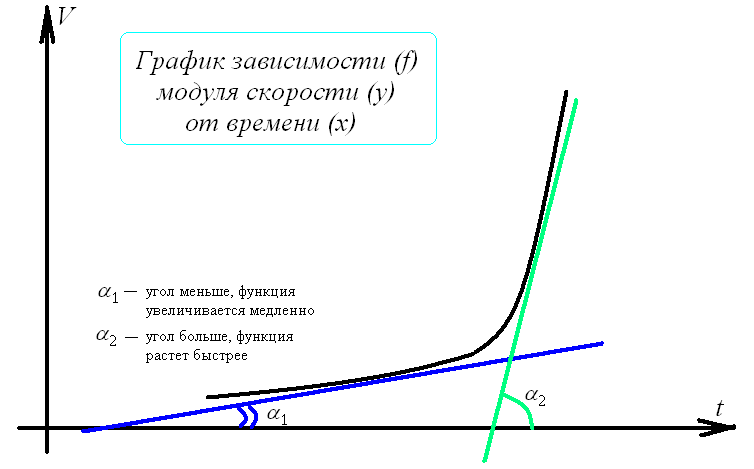
«Игра слов».
Надо различать:

вектор

модуль вектора V 10 м/с
проекцию вектора на ось Vx 8 м/с
с

 оставляющая
вектора
оставляющая
вектора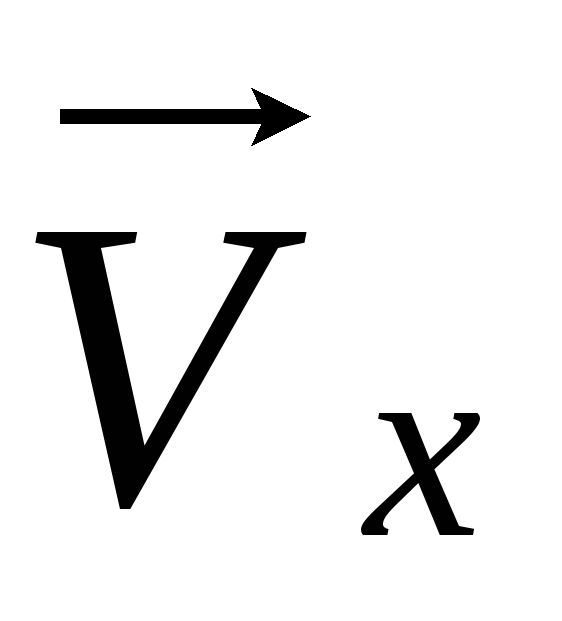
изменение вектора
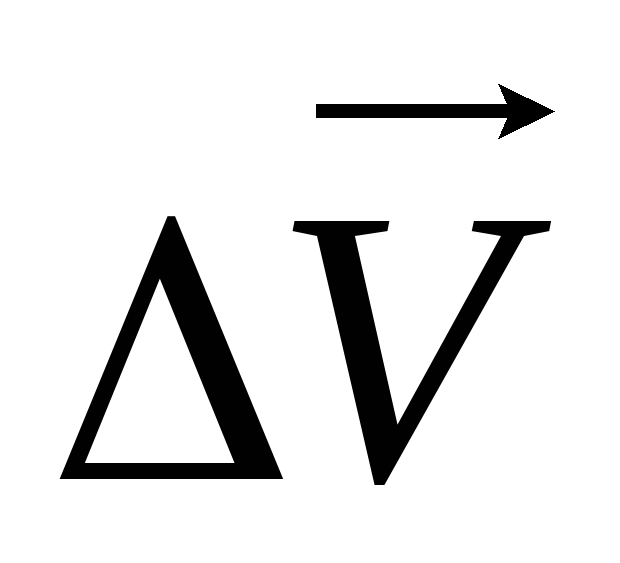
изменение модуля вектора
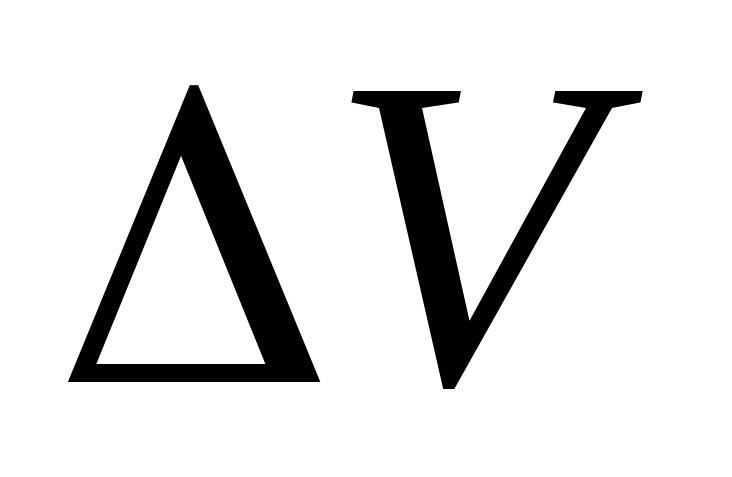 2 м/с
2 м/смодуль изменения вектора
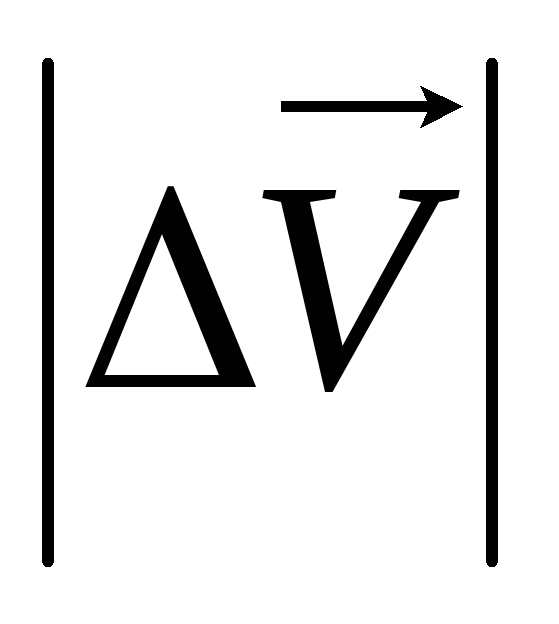 3 м/с
3 м/с
Не путайте скалярные величины с векторными!!!!!
Действия с векторами
В физике переменные могут быть не только скалярами (числами), но и векторами (стрелками).
Поэтому важно уметь осуществлять основные операции над векторами:
Складывать и вычитать
Умножать скалярно и векторно
Проектировать на ось (направление)
Раскладывать на составляющие
Определять модуль и направление
и т.д.
Сложение.
Правило треугольника:
выбрать точку
отложить от нее первый вектор
от конца первого вектора отложить второй вектор
соединить начало первого с концом последнего – это вектор суммы
Правило параллелограмма:
выбрать точку
отложить от нее оба вектора
достроить до параллелограмма
из этой же точки провести диагональ параллелограмма – это вектор суммы
Скалярное умножение.
Перемножая два вектора скалярно получаем ЧИСЛО, которое равно произведению их модулей на косинус угла между ними:
![]()
Умножение вектора на число.
![]()
|
|
полученный вектор
будет в
|
|
|
полученный вектор
будет в
|
|
|
полученный вектор будет направлен в ту же сторону |
|
|
полученный вектор будет направлен в противоположную сторону |
4. Проектирование вектора на направление (на ось).
Находим проекцию вектора на направление:
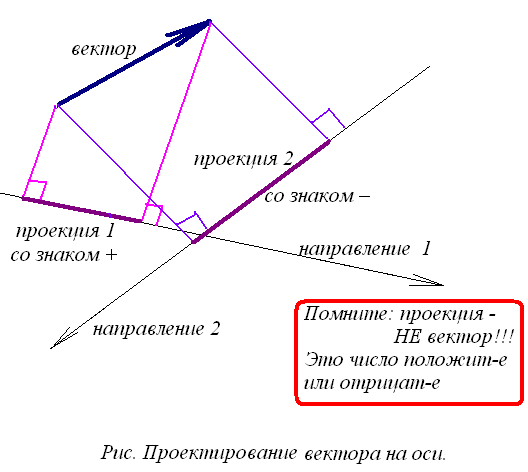
Проверяется в тестах:
А – знание определений, понятий, терминов
В – знание законов и формул
С – умение применять формулы и законы в задачах
Д – графики и схемы
Е – погрешности
А – 10%, В – 20%, С – 30%, Д – 30%, Е – 10%

Основные этапы решения физической задачи
Прочтение и анализ (см. ниже) условия задачи.
Запись данных (см. замечание ниже) с учетом используемых (принятых) обозначений.
Изображение объекта рассмотрения на рисунке, целостно отражающем заданную конкретную ситуацию (создание и графическое изображение физической модели задачи).
Установление взаимосвязей между данными и искомыми величинами на основе определенийфизических величин, физическихзаконов,принципов,теореми др. Запись равенств (формул) отражающих эти взаимосвязи с учетом выбранных в пункте 3 обозначений (запись математической модели задачи).
Обсуждение замкнутости системы записанных уравнений, т.е. возможности нахождения всех искомых величин на основе подсчета числа неизвестных и количества независимых равенств5.
Получение решения задачи в общем виде.
Проверка размерности.
Вычисление значений физических величин и указание единиц их измерения.
Формулирование ответа (полного) на вопрос задачи.
Анализ условия задачи:
уяснить смысл всех слов и научных терминов, встречающихся в условии задачи (не следует пытаться решать задачу, пока не понятно, о чем в ней идет речь!);
пересказать условие задачи в последовательности, отражающей причинно-следственную связь явлений;
выделить основные взаимосвязи между данными и искомыми величинами.
Замечание.Общепринятые обозначения физических величин (например, силы тока - I, сопротивления - R и т.д.), входящие в общем случае в формулы законов, определений и пр., отличаются (например, присутствием индексов) от обозначений данных из условия задачи, носящих конкретный характер (например, сила тока в данном резисторе – I1, сопротивление амперметра – RA и др.). Поэтому перед записью формулы специально необходимо оговаривать, для какого объекта она записывается, и соблюдать соответствующие обозначения (отраженные, прежде всего, в “Дано:”). Записывать тот или иной закон (формулу) в том виде, в каком он записан в тексте параграфа учебника или в ином источнике, в решении конкретной задачи нежелательно, т.к. зачастую такая запись приводит (при невдумчивом решении) к ошибкам и путаницам.