ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 478
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Примеры решения задач
З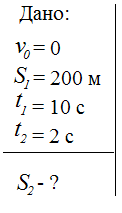 адача-пример
1.Тело, выведенное
из состояния покоя, двигаясь равноускоренно,
прошло 200 м за 10 с. Какое расстояние
прошло тело за 2 с от начала движения?
адача-пример
1.Тело, выведенное
из состояния покоя, двигаясь равноускоренно,
прошло 200 м за 10 с. Какое расстояние
прошло тело за 2 с от начала движения?
Р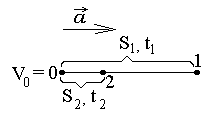 ешение:
Необходимо рассмотреть несколько
состояний, которые условимся называть:
начальное, 1-е и 2-е. В каждом из них
движение характеризуется значением
скорости, пройденным от начала
движения расстоянием за соответствующий
промежуток времени.
ешение:
Необходимо рассмотреть несколько
состояний, которые условимся называть:
начальное, 1-е и 2-е. В каждом из них
движение характеризуется значением
скорости, пройденным от начала
движения расстоянием за соответствующий
промежуток времени.
По условию движение является равноускоренным. Так как о положении тела по отношению к другим телам ничего не говорится, то записываем закон равноускоренного движения для пройденного пути (форма 1, см. ф-лу (2)):
![]() тогда
тогда![]() .
Для участков 0-1 и 0-2 получаем соответственно
конкретные равенства:
.
Для участков 0-1 и 0-2 получаем соответственно
конкретные равенства:![]() и
и![]() .
Делим одно на другое и выражаем искомое
расстояние:
.
Делим одно на другое и выражаем искомое
расстояние:
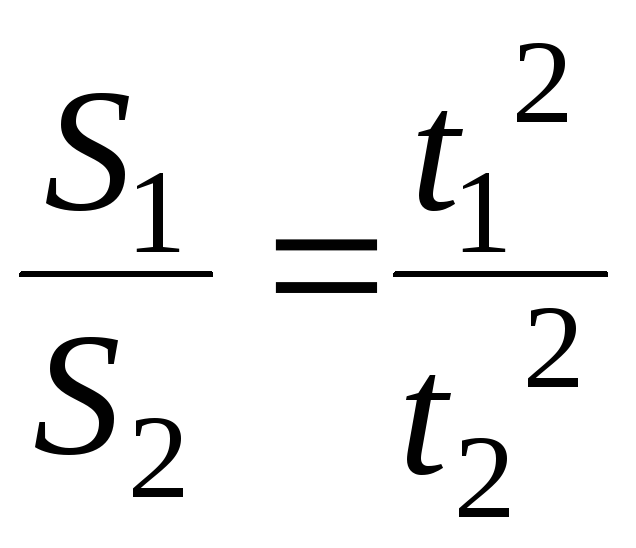
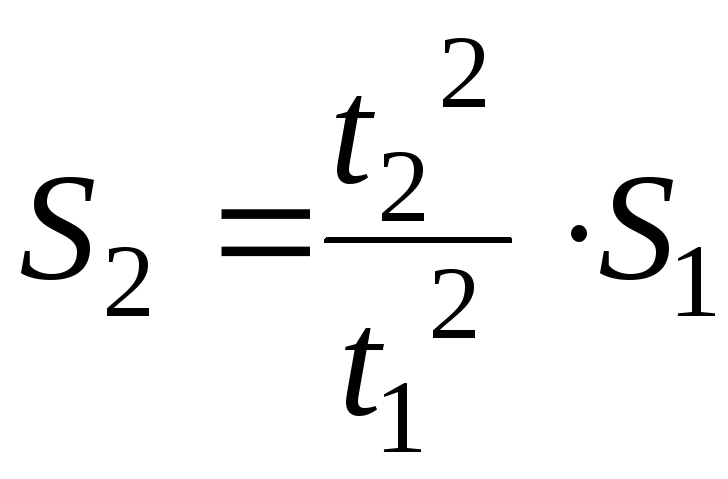 .
Вычисляем:
.
Вычисляем:![]() (м).
(м).
Ответ: за 2сот начала движения тело пройдет 8 м.
З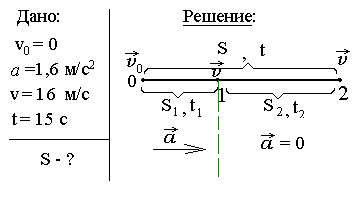 адача-пример
2.Автомобиль
остановился у светофора. После того,
как загорелся зеленый сигнал, он начинает
двигаться с ускорением 1,6 м/с2
и движется так до тех пор, пока скорость
не станет равна 57, 6 км/ч, после чего он
продолжает движение с постоянной
скоростью. На каком расстоянии от
светофора автомобиль окажется спустя
5 с (10 с и 15 с) после появления зеленого
сигнала?
адача-пример
2.Автомобиль
остановился у светофора. После того,
как загорелся зеленый сигнал, он начинает
двигаться с ускорением 1,6 м/с2
и движется так до тех пор, пока скорость
не станет равна 57, 6 км/ч, после чего он
продолжает движение с постоянной
скоростью. На каком расстоянии от
светофора автомобиль окажется спустя
5 с (10 с и 15 с) после появления зеленого
сигнала?
Прежде всего необходимо ответить на вопрос: Как движется тело? Ответ «равноускоренно» – неверен! В условии четко сказано, что тело движется равноускоренно лишь до определенного момента, который надо обязательно учесть, а значит и показать на рисунке – до положения 1 тело движется равноускоренно, затем равномерно с заданной скоростью. Таким образом, характер движения зависит от величины заданного промежутка времени!
Итак, пройденное расстояние складывается
из пути при равноускоренном движении
и пути при равномерном движении: S
= S1+S2,
где![]() и
и![]() .
Здесь
.
Здесь![]() -
время равноускоренного движения от
начальной нулевой скорости до известной
конечной скорости, равной
-
время равноускоренного движения от
начальной нулевой скорости до известной
конечной скорости, равной![]() .
Найдем его из зависимости скорости от
времени при равноускоренном движении
(см. ф-лу (4)):
.
Найдем его из зависимости скорости от
времени при равноускоренном движении
(см. ф-лу (4)):![]()
![]() .
Тогда
.
Тогда![]() и
и![]() .
Находим искомое расстояние, подставляя
найденные выражения:
.
Находим искомое расстояние, подставляя
найденные выражения:![]() .
.
Мы получили, вроде бы, общее решение.
Решим задачу с учетом конкретных данных.
Вычислим время, необходимое для достижения
заданной скорости при движении с данным
ускорением :
![]() (с). Тогда делаем вывод, что в случае,
когда t = 5 с, все 5 с тело будет двигаться
равноускоренно и получаем:
(с). Тогда делаем вывод, что в случае,
когда t = 5 с, все 5 с тело будет двигаться
равноускоренно и получаем:![]() .
Вычисляем:
.
Вычисляем:![]() (м). Если же t = 15 с, то используем полученную
общую формулу в полном объеме и получаем
значение:
(м). Если же t = 15 с, то используем полученную
общую формулу в полном объеме и получаем
значение:![]() (м).
При этом
(м).
При этом![]() (м)
и
(м)
и![]() (м).
Кроме того, если задано t = 10 с, то можно
воспользоваться как формулой для S1,
так и общей формулой для S:
(м).
Кроме того, если задано t = 10 с, то можно
воспользоваться как формулой для S1,
так и общей формулой для S:![]() (м)
или
(м)
или![]() (м).
(м).
Итак, общее решение задачи должно правильно давать ответы для всевозможных числовых значений заданных в условии величин! Тогда с учетом этого наше общее решение будет иметь такой вид:
![]() при
при![]() и
и![]() при
при![]() .
.
Ответ: спустя 5 с после появления зеленого сигнала автомобиль окажется на расстоянии 20 м от светофора; через 10 с он будет на расстоянии 80 м, а через 15 с – на расстоянии 160 м от него.
Замечание. Важно отметить, что полученная общая формула является формулой зависимости пути от времени, т.е. законом движения автомобиля после включения зеленого сигнала светофора, записанным в форме, выражаемой формулой (2). Т.е. приведенная в качестве примера задача относится к группе задач, решаемых на основе записи закона движения тела в форме «зависимости пути от времени» (форма 1). Другая группа задач по кинематике предполагает запись закона движения выбранного тела в форме 2 – «зависимости координаты от времени» (см. формулу (3)).
Задача-пример 3.Тело брошено с высоты H0 = 20 м вертикально вверх со скоростью V0 = 5 м/с. Где будет находиться тело через время t = 0,5; 1; 2; 10 с? Найти время полета тела.
Анализируя условие задачи, убеждаемся
в том, что в данном случае имеет значение
положениетела (требуется ответить
на вопрос «Где?»), т.е. его координата
(движение одномерное – вдо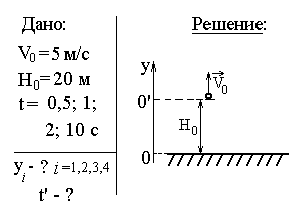 ль
одной прямой, значит достаточно одной
координаты, чтобы точно задать положение
тела), задающая положение тела по
вертикали. Отсюда делаем вывод о
необходимости задания оси координат
(направленной прямой с началом отсчета
и масштабом). Ось выбирается вдоль
направления движения, ее направление
можно выбрать двояко (вверх или вниз),
а начало отсчета можно брать влюбойточке. Этот момент в решении задачи
содержит некоторый «произвол» решающего.
Выбор направления оси скажется на знаке
перед векторными величинами в записи
закона движения (только и всего!), а
положение начала отсчета должно будет
учитываться при определении начальной
координаты тела и при задании его
положения соответствующими координатами.
Второй момент требует рационального
выбора начала отсчета с учетом условия
задачи.
ль
одной прямой, значит достаточно одной
координаты, чтобы точно задать положение
тела), задающая положение тела по
вертикали. Отсюда делаем вывод о
необходимости задания оси координат
(направленной прямой с началом отсчета
и масштабом). Ось выбирается вдоль
направления движения, ее направление
можно выбрать двояко (вверх или вниз),
а начало отсчета можно брать влюбойточке. Этот момент в решении задачи
содержит некоторый «произвол» решающего.
Выбор направления оси скажется на знаке
перед векторными величинами в записи
закона движения (только и всего!), а
положение начала отсчета должно будет
учитываться при определении начальной
координаты тела и при задании его
положения соответствующими координатами.
Второй момент требует рационального
выбора начала отсчета с учетом условия
задачи.
В нашем случае в задаче известна высота, с которой брошено тело, соответственно хотелось бы ответить на поставленный вопрос указанием соответствующего расстояния от поверхности Земли до искомого положения тела. Поэтому выбираем начало отсчета так, чтобы высота тела над землей была равна его координате, т.е. у поверхности Земли.
Ясно, что закон движения теперь надо
записывать в форме 2. Определим сначала
вид движения. Неверно сказать, что тело
движется «равнозамедленно» (так лишь
на участке движения вверх) или
«равноускоренно» (так лишь на участке
движения вниз). Правильно будет сказать,
что тело движется с постоянным ускорением
под действием силы тяжести, т.е.
![]() =
= const. Получаем:
=
= const. Получаем:
![]() - этообщаяформула зависимости
- этообщаяформула зависимости![]() от
от![]() .
Подставляя вместо одной из этих переменных
некоторое ее значение (например,t1),
автоматически вместо второй переменной
становитсясоответствующее значение
(y1)
и наоборот. Это очень важное для понимания
обстоятельство ложится в основу получения
конкретных равенств.
.
Подставляя вместо одной из этих переменных
некоторое ее значение (например,t1),
автоматически вместо второй переменной
становитсясоответствующее значение
(y1)
и наоборот. Это очень важное для понимания
обстоятельство ложится в основу получения
конкретных равенств.
Итак, при t = t1 y = y1, т.е. подставляем и получаем:
![]() ,
аналогично для всех данных в условии
значений времени. Но!!! Учитывая физическую
сущность задачи (в отличие от математических
абстракций, выраженных формулами), надо
заметить, что координата тела различна
лишь когда тело движется (изменяет
положение в пространстве). Иначе говоря,
если тело перестает двигаться, то для
всех последующих значений времени ее
координата остается неизменной! В нашем
случае, когда тело упадет на Землю, его
координата станет равной нулю и будет
таковой для всех значений времени
,
аналогично для всех данных в условии
значений времени. Но!!! Учитывая физическую
сущность задачи (в отличие от математических
абстракций, выраженных формулами), надо
заметить, что координата тела различна
лишь когда тело движется (изменяет
положение в пространстве). Иначе говоря,
если тело перестает двигаться, то для
всех последующих значений времени ее
координата остается неизменной! В нашем
случае, когда тело упадет на Землю, его
координата станет равной нулю и будет
таковой для всех значений времени![]() ,
гдеt’–
время полета тела (время его движениянадповерхностью Земли). Его значение
ищем подстановкой:
,
гдеt’–
время полета тела (время его движениянадповерхностью Земли). Его значение
ищем подстановкой:
при t = t’ y =0, т.е.
![]() .
Решаем это квадратное уравнение, приведя
предварительно его к виду приведенного
квадратного уравнения:
.
Решаем это квадратное уравнение, приведя
предварительно его к виду приведенного
квадратного уравнения:
![]() ,
,
![]() ,
значит математически имеется два корня:
,
значит математически имеется два корня:
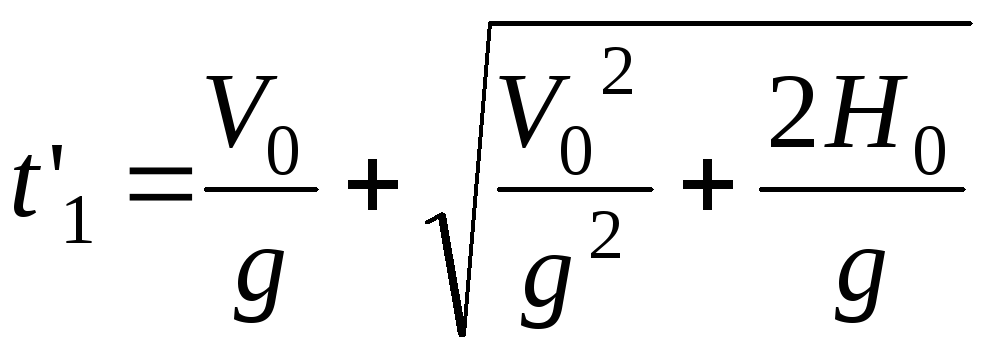 и
и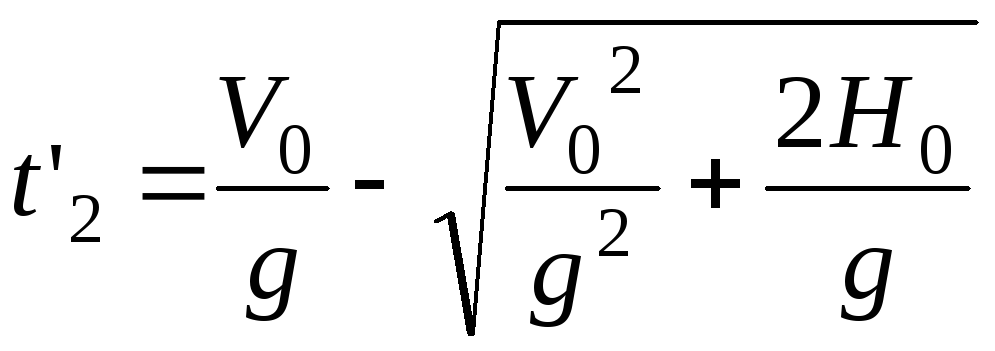 .
.
Очевидно, что второй корень при любых значениях начальной скорости будет отрицательным, а значит задача имеет лишь единственное физическое решение:
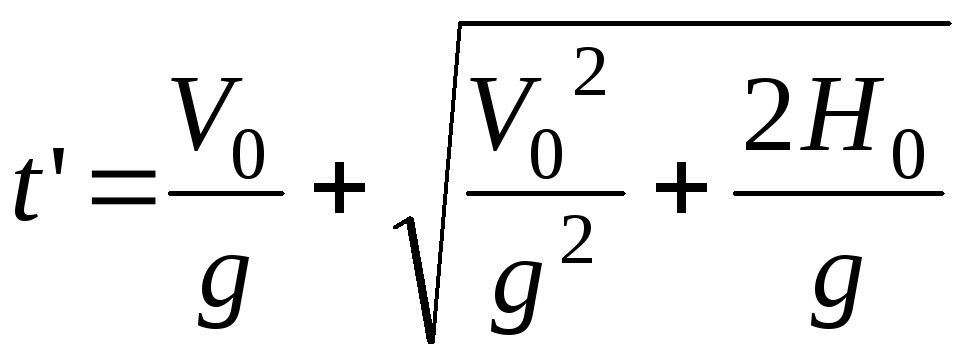 .
.
Вычисляем
![]() (с) – искомое время полета тела. Теперь
можно сказать, чему равна координата
тела, например, приt4= 10 с:y4
= 0.
(с) – искомое время полета тела. Теперь
можно сказать, чему равна координата
тела, например, приt4= 10 с:y4
= 0.