ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 488
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Движение по наклонной плоскости
За какое время t тело массойmсоскользнет с наклонной плоскости высотойh, наклоненной под угломк горизонту, если по наклонной плоскости с углом наклонаоно движется равномерно?.[
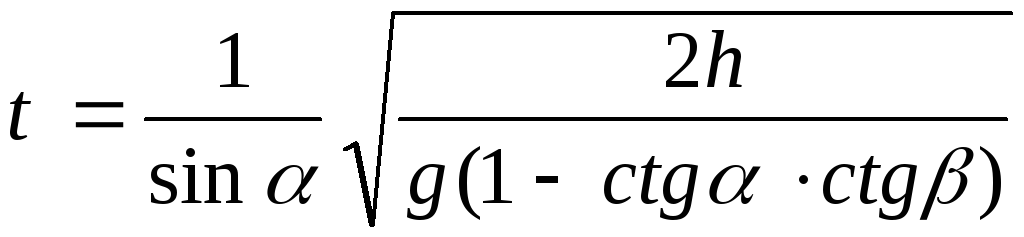 ]
]Чтобы определить коэффициент трения между деревянными поверхностями, брусок положили на доску и стали поднимать один конец доски до тех пор, пока брусок не начал по ней скользить. Это произошло при угле наклона доски 140. Чему равен коэффициент трения?[0,25]
Груз движется вверх по наклонной плоскости (угол наклона к горизонту) с постоянным ускорениемапод действием силы, параллельной наклонной плоскости и совпадающей по направлению с вектором ускорения. На какую величинуследует увеличить коэффициент трения груза о плоскость, чтобы тело поднималось равномерно?
Тело лежит на наклонной плоскости, составляющей с горизонтом угол 450. а) При каком предельном коэффициенте трения тело начнет скользить по наклонной плоскости? б) С каким ускорением будет скользить тело по плоскости, если коэффициент трения равен 0,03? в) Сколько времени потребуется для прохождения при этих условиях 100 м пути? г) Какую скорость тело будет иметь в конце пути?
Ледяная горка составляет с горизонтом угол = 300. По ней пускают снизу вверх камень, который в течениеt1= 2 с проходит расстояние 16 м, после чего скатывается вниз? Каков коэффициент трения между горкой и камнем?
Два бруска с одинаковыми массами скреплены нитью и находятся на наклонной плоскости с углом наклона . Определить натяжение нитиТпри движении брусков вдоль наклонной плоскости, если коэффициент трения верхнего брускав 2 раза больше коэффициента трения нижнего.
Брусок скользит с наклонной плоскости длиной l и высотойhи далее по горизонтальной плоскости на расстояниеS, после чего остановился. Определить коэффициент трения бруска, считая его постоянным.
Через какое время скорость тела, которому была сообщена скорость V0, направленная вверх по наклонной плоскости, снова будет равнаV0? Коэффициент трения,угол наклона плоскости к горизонту. Тело начинает двигаться со скоростьюV0, находясь посередине наклонной плоскости.
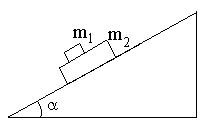
Два бруска массой 0,2 каждый поместили на наклонную плоскость с углом 450, как показано на рисунке. Коэффициент трения нижнего бруска о наклонную плоскость1= 0,3, верхнего2= 0,1. Определить силу взаимодействия брусков при их совместном соскальзывании с наклонной плоскости.
Н
 а
наклонную плоскость с углом наклона
помещена плоская плита массойm2,
а на нее – брусокm1.
Коэффициент трения между бруском и
плитой1.
Определить, при каких значениях
коэффициент трения2между плитой и плоскостью плита не
будет двигаться, если известно, что
брусок скользит по плите.
а
наклонную плоскость с углом наклона
помещена плоская плита массойm2,
а на нее – брусокm1.
Коэффициент трения между бруском и
плитой1.
Определить, при каких значениях
коэффициент трения2между плитой и плоскостью плита не
будет двигаться, если известно, что
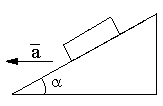
брусок скользит по плите.Наклонная плоскость с углом наклона движется с ускорениема. Начиная с какого значения ускоренияатело, лежащее на наклонной плоскости, начнет подниматься? Коэффициент трения между телом и наклонной плоскостью равен.
Ч
 ему
должен быть равен минимальный коэффициент
трения между шинами и поверхностью
наклонной дороги с уклоном 300,
чтобы автомобиль мог двигаться по ней
вверх с ускорением 0,6 м/с2?
ему
должен быть равен минимальный коэффициент
трения между шинами и поверхностью
наклонной дороги с уклоном 300,
чтобы автомобиль мог двигаться по ней
вверх с ускорением 0,6 м/с2?Брусок массой 0,5 кг лежит на шероховатой поверхности, наклоненной к горизонту под углом . С какой минимальной горизонтальной силойF, направленной перпендикулярно плоскости чертежа, нужно подействовать на брусок, чтобы он сдвинулся с места. Коэффициент трения = 0,7.
Н
 а
наклонной плоскости находится груз
массойm1= 5 кг, связанный нитью, перекинутой
через блок, с другим грузомm2.
Коэффициент трения между первым грузом
и плоскостью 0,1. Угол наклона плоскости
к горизонту 370. При каких значениях
массы m2система будет находиться
в равновесии?
а
наклонной плоскости находится груз
массойm1= 5 кг, связанный нитью, перекинутой
через блок, с другим грузомm2.
Коэффициент трения между первым грузом
и плоскостью 0,1. Угол наклона плоскости
к горизонту 370. При каких значениях
массы m2система будет находиться
в равновесии?Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы 300и 450. Гири равной массы по 1 кг соединены нитью и перекинуты через блок. Найти: 1) ускорение, с которым движутся гири; 2) натяжение нити. Коэффициенты трения гирь о наклонные плоскости равны 0,1. Трением в блоке пренебречь.
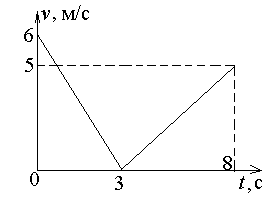
Шайба, брошенная вдоль наклонной плоскости, скользит по ней, двигаясь вверх, затем возвращается к месту броска. График зависимости модуля скорости шайбы от времени приведен на рис. Найти угол наклона плоскости к горизонту и максимальную высоту подъема шайбы.
По наклонной плоскости с углом наклона 300движутся как одно целое (с одинаковым ускорением) брускиm1=1 кг,m2=2 кг. Коэффициенты трения между наклонной плоскостью и этими брусками соответственно равны1=0,25 и2=0,10. Найти силуRвзаимодействия между брусками в процессе движения.
*Тело массой m1поднимается по наклонной плоскости с ускорениемапод действием силыF, параллельной наклонной плоскости и направленной в сторону движения тела. На какую величинуmследует увеличить массу тела, чтобы оно поднималось равномерно? Коэффициент трения, величина и направление силыFне меняется.
Груз массой mсвободно двигается вниз по наклонной плоскости (угол наклонак горизонту) с некоторым постоянным ускорением. Какую силуFпараллельно наклонной плоскости и направленную вверх нужно приложить к грузу, чтобы он поднимался с тем же ускорением? Коэффициент трения постоянен.
Действие сил при вращательном движении
Груз, подвешенный на нити длиной 5 м, равномерно вращается по окружности в горизонтальной плоскости. Найти угловую скорость вращения, если при вращении нить отклонилась от вертикали на угол 600.[2]
Найти отношение сил, с которыми танк давит на середины выпуклого и вогнутого мостов. Радиус кривизны мостов в обоих случаях равен 40 м, а скорость движения равна 45 км/ч. [0,43]
Автомобиль массой 8 т движется со скоростью 36 км/ч по выпуклому мосту радиусом 200 м. Определить силу, действующую на автомобиль в верхней точке моста. Ускорение свободного падения принять равным 10 м/с2.[7,6104 Н]
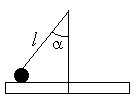
На невесомом стержне висит груз массой m. Груз отклоняют на угол= 900и отпускают. Найти натяжение стержня при прохождении им положения равновесия.
Тяжелый шарик подвешен на нити длиной l. Нить равномерно вращается в пространстве, образуя с вертикалью угол. Сколько оборотов делает шарик за времяt.
С какой минимальной угловой скоростью нужно вращать ведро в вертикальной плоскости, чтобы из него не выливалась вода? Расстояние от поверхности воды до центра вращенияl. [ 2=g/l]
Ведерко с водой, привязанной к веревке длиной l, вращается в вертикальной плоскости. найти натяжение веревки в высшей и низшей точках окружности при условии, что вода не выливается в верхней точке. Масса ведерка с водойm. [T1=0,T2=2mg]
Тяжелый шарик массы m подвешен на нити длины l. Шарик равномерно вращается по кругу в горизонтальной плоскости (конический маятник). Нить при этом отклонена на угол. Найти время полного оборота шарика.
Математический маятник имеет массу mи длинуl. В момент, когда он образует уголс вертикалью, его скорость равнаV. Какова в этот момент сила натяжения нити?
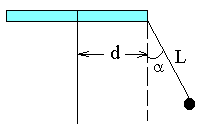
На вращающемся горизонтальном диске укреплен отвес, который устанавливается под углом = 450к вертикали. Расстояние от точки подвеса до оси вращенияd= 10 см, длина нитиL = 6 см. определить угловую скорость вращения.[8,3 с-1]
К
 онькобежец
движется со скоростью 10 м/с по окружности
радиусом 30 м. Под каким углом к горизонту
он должен наклониться, чтобы сохранить
равновесие.
онькобежец
движется со скоростью 10 м/с по окружности
радиусом 30 м. Под каким углом к горизонту
он должен наклониться, чтобы сохранить
равновесие.Груз массой m= 100 г подвешен на нити и совершает колебания, отклоняясь на угол= 600в ту и другую сторону. Определить натяжение нити в момент, когда нить составляет угол= 300с вертикалью.
Автомобиль движется в верхней части выпуклого моста радиуса R= 40 м. Какое максимальное горизонтальное ускорение может развить автомобиль в этой точке, если его скорость 54 км/ч, а коэффициент трения колес автомобиля о мост 0,6. При какой скоростиV1в верхней точке автомобиль не может увеличивать модуль скорости?
Ч
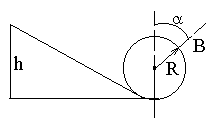 еловек
сидит на краю круглой горизонтальной
платформы радиусом 4 м. С какой частотой
(об/мин) должна вращаться платформа
вокруг вертикальной оси, чтобы человек
не мог удержаться на ней при коэффициенте
трения 0,27?
еловек
сидит на краю круглой горизонтальной
платформы радиусом 4 м. С какой частотой
(об/мин) должна вращаться платформа
вокруг вертикальной оси, чтобы человек
не мог удержаться на ней при коэффициенте
трения 0,27?Самолет делает «мертвую петлю» с радиусом 100 м и движется по ней со скоростью 280 км/ч. С какой силой тело летчика массой 80 кг будет давить на сиденье самолета в верхней и нижней точках петли?
Математическому маятнику массой mсообщили минимальный толчок, чтобы он совершил полный оборот в вертикальной плоскости. Какова сила натяжения нити маятника при прохождении им положения равновесия?
Шарик скользит по желобу с высоты hи затем движется по «мертвой петле» радиусаR. Какое давление производит шарик на желоб в некоторой точке В, если радиус, проведенный из центра петли в точку В, составляет с вертикалью угол? Масса шарикаm, высотаh = 5R/2. Размеры шарика считать ничтожно малыми.
В
 округ
вертикально расположенного стержня
вращается насаженный на него диск. На
диске находится шарик, прикрепленный
к стержню нитью, длиныlи составляющий уголсо стержнем. С каким периодом должна
вращаться система, чтобы нить не
провисала при таком положении шарика?
округ
вертикально расположенного стержня
вращается насаженный на него диск. На
диске находится шарик, прикрепленный
к стержню нитью, длиныlи составляющий уголсо стержнем. С каким периодом должна
вращаться система, чтобы нить не
провисала при таком положении шарика?**Обруч радиуса Rукреплен вертикально на полу. С вершины обруча соскальзывает без трения тело. На каком расстоянииl от точки закрепления обруча упадет это тело?[1,5R]
Материальная точка массой 11 кг движется по криволинейной траектории под действием равнодействующей силы 20 Н. Определить скорость точки в момент времени, когда радиус кривизны траектории равен 15 м и угол между силой и вектором скорости равен 350.[3,96 м/с]
В
 лифте, движущемся вертикально вверх с
ускорениема0
= 4 м/с2, находится горизонтальный
столик, вращающийся с угловой скоростью4рад/с. Зная, что коэффициент трения
коробка о столик равен 0,4, найти
максимальное расстояние коробка от
оси вращения, при котором он еще будет
удерживаться на столике. [3,5 см]
лифте, движущемся вертикально вверх с
ускорениема0
= 4 м/с2, находится горизонтальный
столик, вращающийся с угловой скоростью4рад/с. Зная, что коэффициент трения
коробка о столик равен 0,4, найти
максимальное расстояние коробка от
оси вращения, при котором он еще будет
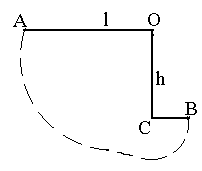
удерживаться на столике. [3,5 см]Шарик массой m, висящий на нити длиныl, отводят в сторону так, что нить занимает горизонтальное положение А, и отпускают без толчка. Внизу на расстоянииh= (2/3)lпод точкой подвеса О вбит гвоздь С. Какую силу натяжения будет иметь нить в момент, когда она займет горизонтальное положение В?