ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 479
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Примеры решения задач
З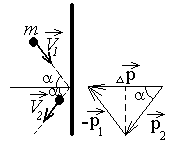 адача-пример
1.Тело массой 20 г
движется со скоростью 10 м/с под углом
600
к вертикальной стенке. Определить
изменение импульса тела в результате
абсолютно упругого столкновения его
со стенкой.
адача-пример
1.Тело массой 20 г
движется со скоростью 10 м/с под углом
600
к вертикальной стенке. Определить
изменение импульса тела в результате
абсолютно упругого столкновения его
со стенкой.
Р
Дано: m= 0,02 кг V= 10 м/с = 600 р
- ?
 ешение:
Делаем рисунок: указываем направление
скорости тела до и после удара о стенку.
Напраление импульса совпадает с
направлением соответствующей скорости.
Т.к. удар о стенку считается абсолютно
упругим, то величина скорости (а значит
и импульса) не меняется. Изменением
направления скорости показано на
рисунке.
ешение:
Делаем рисунок: указываем направление
скорости тела до и после удара о стенку.
Напраление импульса совпадает с
направлением соответствующей скорости.
Т.к. удар о стенку считается абсолютно
упругим, то величина скорости (а значит
и импульса) не меняется. Изменением
направления скорости показано на
рисунке.
Далее, записываем формулу изменения
импульса:
![]() и на ее основе строим «треугольник
импульсов», из которого геометрически
находим длину нужной стороны, равную
искомой физической величине: т.к.
и на ее основе строим «треугольник
импульсов», из которого геометрически
находим длину нужной стороны, равную
искомой физической величине: т.к.![]() ,
то
,
то
![]() - модуль изменения импульса. А направлен
вектор
- модуль изменения импульса. А направлен
вектор![]() перпендикулярно стенке от нее.
перпендикулярно стенке от нее.
Вычисляем:
![]() (кгм/с).
(кгм/с).
Ответ: 0,2 кгм/с в перпендикулярном к стенке направлении от нее.
Методические указания. Прежде всего заметим, что изменение векторной величины – тоже вектор. А поэтому ответ на вопрос задачи состоит из числового значения и описания его направления. Далее примечательно проанализировать полученный ответ. В частности, как можно без построения «треугольника импульсов» определить направление вектора изменения импульса тела? Чтобы ответить, необходимо обратиться к формуле (4.17): вектора, стоящие справа и слева от знака равенства одинаково направлены, т.е. изменение импульса всегда имеет такое же направление, как и сила, его вызывающая. В данном примере изменение импульса происходит под действием силы реакции опоры (стенки), которая, как известно, всегда перпендикулярна опоре и направлена от нее.
Полученному в задаче значению равен и импульс силы реакции стенки, в соответствии с законом (4.17). Т.е. чтобы найти импульс силы, вовсе не обязательно знать ее значение и время ее действия. К тому же сила в течение промежутка времени своего действия на тело может быть далеко не постоянной по модулю величиной: в начале большей, а в конце меньшей!
Задача-пример 2. Конькобежец, стоя на коньках на льду, бросает груз массой 10 кг под углом 300 к горизонту со скоростью 5 м/с. Какова будет начальная скорость движения конькобежца, если его масса равна 64 кг? Перемещение конькобежца во время броска пренебречь.
Р Дано: m1= 10 кг m2= 64 кг V1= 5 м/c =
300 V2
- ?
 ешение:
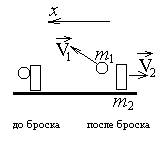
На рисунке указываем векторы импульсов
тел до и после изменения их движения и
положительное направление координатной
оси (по горизонтали в
ешение:
На рисунке указываем векторы импульсов
тел до и после изменения их движения и
положительное направление координатной
оси (по горизонтали в
 4.18*):
4.18*):![]() ,
где
,
где![]() -
проекция импульса данной системы до
броска, а
-
проекция импульса данной системы до
броска, а![]() - после броска. Учитывая, что проекция
импульса системы равна сумме проекций
импульсов ее частей и до броска оба
тела покоились (суммарный импульс
системы равен нулю), получаем скалярное
равенство:
- после броска. Учитывая, что проекция
импульса системы равна сумме проекций
импульсов ее частей и до броска оба
тела покоились (суммарный импульс
системы равен нулю), получаем скалярное
равенство:![]() ,
отсюда выражаем:
,
отсюда выражаем:
![]() .
Вычисляем:
.
Вычисляем:![]() (м/с). Знак «–» означает (исходя из
определения проекции вектора на ось),
что скорость конькобежца после броска
направлена противоположно выбранному
положительному направлению оси, т.е.
груз и человек будут двигаться по
горизонтали в противоположных
направлениях.
(м/с). Знак «–» означает (исходя из
определения проекции вектора на ось),
что скорость конькобежца после броска
направлена противоположно выбранному
положительному направлению оси, т.е.
груз и человек будут двигаться по
горизонтали в противоположных
направлениях.
Ответ: 0,68 м/с в сторону от груза по горизонтали
Методические указания. Возможны два варианта решения: 1) когда мы сразу можем точно установить (и обосновать выбор) истинное направление скорости после ее изменения, тогда изображаем ее на рисунке и в равенство входит модуль этой скорости, откуда его и находим; 2) истинное направление движения после события неизвестно, тогда на рисунке скорость не указывается или рисуется произвольно, а в равенство входит ее проекция на ось. Далее по найденному значению проекции, с учетом ее знака, дается ответ о значении и направлении искомой скорости.
Решенная выше задача демонстрирует второй вариант.
Задача-пример 3. На какое расстояние сместится неподвижно стоящая на воде лодка, если человек массой m1 = 70 кг пройдет с носа лодки на корму? Длина лодки 2,5 м, ее масса m2 = 100 кг. Сопротивлением воды пренебречь.
Дано: m1= 70 кг m2= 100 кг l= 2,5 м
х-?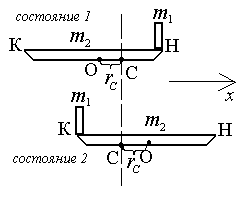

 Решение: В данной задаче имеем дело уже
не с одним телом, а с системой двух тел
«лодка-человек». Т.к. в направлении осихна систему не действуют
внешние силы, то при переходе системы
из состояния 1 в состояние 2 ее импульс
не меняется, т.е. остается равен нулю.
Тогда получаем, что скорость центра
масс системы тоже остается равна нулю
в течение всего перехода, т.е. точка С
(рис.) неподвижна в процессе перехода
человека с носа лодки на корму.
Решение: В данной задаче имеем дело уже
не с одним телом, а с системой двух тел
«лодка-человек». Т.к. в направлении осихна систему не действуют
внешние силы, то при переходе системы
из состояния 1 в состояние 2 ее импульс
не меняется, т.е. остается равен нулю.
Тогда получаем, что скорость центра
масс системы тоже остается равна нулю
в течение всего перехода, т.е. точка С
(рис.) неподвижна в процессе перехода
человека с носа лодки на корму.
Относительно центра лодки (точки О)
радиус вектор точки С меняет лишь
направление: на противоположное (с
«вправо» на «влево»), оставаясь (с учетом
симметрии лодки и положения человека
на ней до и после перехода) одинаковым
по величине и равным в соответствии с
формулой (4.19):
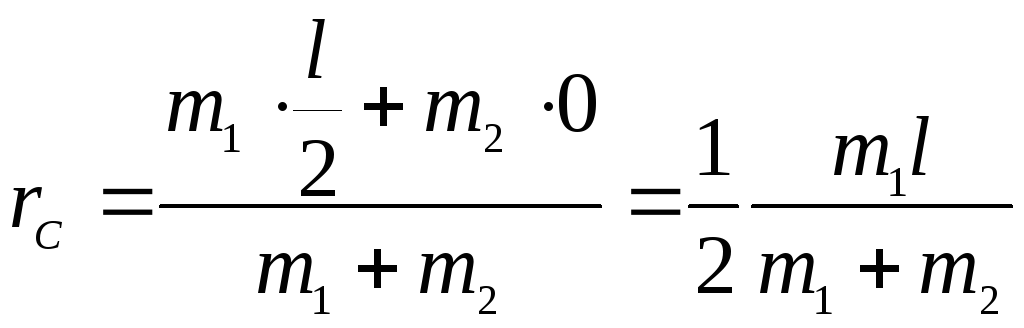 .
Из рисунка видно, что лодка при этом
должна сместиться на расстояние
.
Из рисунка видно, что лодка при этом
должна сместиться на расстояние
![]() .
.
Вычислим:
![]() (м). Ответ: 1 м
(м). Ответ: 1 м
Задача-пример 4. На гладкой горизонтальной плоскости находится тело массы М (рис.) и на нем небольшая шайба массы m. Последней сообщили в горизонтальном направлении скорость v. На какую высоту (по сравнению с первоначальным уровнем) поднимется шайба после отрыва от тела М? Трения нет.
Р
Дано: m М v _________ h-?
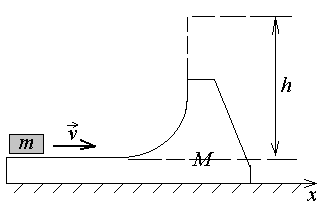
 ешение:
Когда шайбаmначинает
менять направление движения, двигаясь
по изгибу тела М, то тело М вследствие
отсутствия силы трения начинает двигаться
тоже. Считая, что время такого взаимодействия
мало, можно воспользоваться законом
сохранения проекции импульса системы
«M-m» на горизонтальную
осьх:
ешение:
Когда шайбаmначинает
менять направление движения, двигаясь
по изгибу тела М, то тело М вследствие
отсутствия силы трения начинает двигаться
тоже. Считая, что время такого взаимодействия
мало, можно воспользоваться законом
сохранения проекции импульса системы
«M-m» на горизонтальную
осьх:
![]() (I).
(I).
Учтем, что шайба, не отрываясь от тела
М(и после отрыва),
продолжает движение вдоль осихсо
скоростью![]() ,
не меняя ее вследствие отсутствия
горизонтальных сил. Также т.к. в системе
«M-m» отсутствуют
диссипативные силы (сила трения), а
внешние силы (тяжести) потенциальны
(внешнего трения тоже нет), то для нее
выполняется закон сохранения полной
механической энергии:
,
не меняя ее вследствие отсутствия
горизонтальных сил. Также т.к. в системе
«M-m» отсутствуют
диссипативные силы (сила трения), а
внешние силы (тяжести) потенциальны
(внешнего трения тоже нет), то для нее
выполняется закон сохранения полной
механической энергии:
![]() (II).
(II).
Получили систему из двух уравнений
(I)-(II) с двумя
неизвестными![]() иh,
откуда находим искомую величину:
иh,
откуда находим искомую величину:
![]() ,
тогда
,
тогда![]()
![]() и, наконец,
и, наконец,
![]() .
.
Ответ:
![]()
Задача-пример 5. С какой силой нужно надавить на верхний груз массы m1, чтобы нижний груз массы m2, соединенный с верхним пружиной, оторвался от пола после прекращения действия этой силы?
Р
Дано: m1 m2
F-?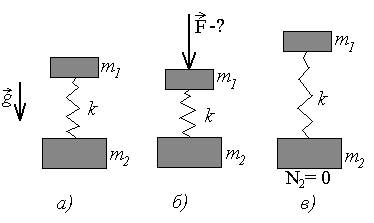

 ешение:
Рассмотрим три состояния системы,
состоящей из двух грузов, соединенных
пружиной. В исходном состоянии (рис.а)
пружина сжата нахи верхний груз находится в равновесии,
поэтому:
ешение:
Рассмотрим три состояния системы,
состоящей из двух грузов, соединенных
пружиной. В исходном состоянии (рис.а)
пружина сжата нахи верхний груз находится в равновесии,
поэтому:![]() .
Далее под действием силы
.
Далее под действием силы![]() пружина сжимается еще на величинух,
верхний груз также уравновешен:
пружина сжимается еще на величинух,
верхний груз также уравновешен:![]() .
В конечном состоянии пружина растянута
на величинуhи
нижний груз не давит на опору:
.
В конечном состоянии пружина растянута
на величинуhи
нижний груз не давит на опору:![]() .
Из полученных трех равенств получаем:
.
Из полученных трех равенств получаем:
![]() - ?. Т.е. теперь ищем величину
- ?. Т.е. теперь ищем величину![]() .
.
Рассмотрим переход системы из второго состояния в третье (рис. б и в). При этом выполняется закон сохранения полной механической энергии:
Е2 = Е3
![]() ,
,
![]() k
k
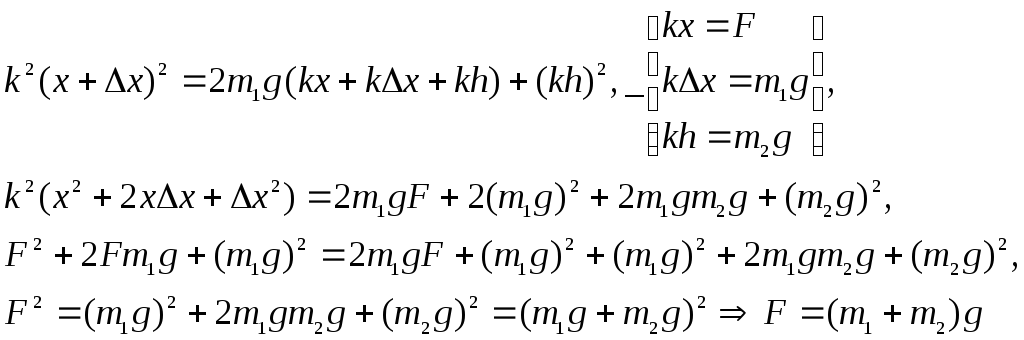
Ответ:
![]()
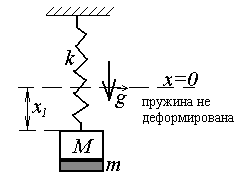
Задача-пример 6. От груза, висящего на пружине жесткости k,отрывается часть массой m. На какую высоту поднимется после этого оставшаяся часть груза.
Р
Дано: k m
x1-x2
-? ешение:
1) До отрыва массыmусловие
равновесия имеет вид:
ешение:
1) До отрыва массыmусловие
равновесия имеет вид:
k x1=(M+m)g
(I), гдеM+m– масса груза,
x1- относительное удлинение пружины.
x1=(M+m)g
(I), гдеM+m– масса груза,
x1- относительное удлинение пружины.
2) рассмотрим два состояния груза без массы m: сразу после отрыва и на искомой высоте, где он НЕ находится в равновесии. При переходе системы (груз на пружине) из первого состояния во второе выполняется закон сохранения полной механической энергии (т.к. действуют лишь потенциальные силы):
![]()
 2
2
![]()
![]() (II).
(II).
Считая, что, поднявшись на искомую
высоту, груз все еще растягивает пружину
(т.е.
![]() ),
т.е. их1их2– деформации растяжения, получим в
качестве искомого расстояния величину
(х1-х2).
),
т.е. их1их2– деформации растяжения, получим в
качестве искомого расстояния величину
(х1-х2).
Имеем:
![]()
![]() .
.