Файл: Методичка по механике вся Печать новый вариант12г.doc

Теория – это взгляд с некой колокольни. С разных колоколен вид свой. А потому современная наука признает комплексный подход, а в физике возник и работает принцип дополнительности.

Истина всегда конкретна. Невозможно судить об истинности утверждения в отрыве от контекста. Контекст же задает и ракурс восприятия смысла используемых слов языка.

Изучение теоретических положений опирается на конкретный контекст. А потому, выучивая закон или определение, умей описать соответствующий контекст ситуации.

Всегда имей смелость знать и иметь свое суждение на тот или иной аспект реальности. Если нет своего суждения, можешь воспользоваться чужим, «арендуемым». Мудрые люди имеют свое суждение, подрастающее поколение сначала пользуется чужими, критически осмысливая на свой манер и формируя свои. «Арендуемые» суждения сменяются по мере познания мира.

Часть первая: КИНЕМАТИКА

Основные термины и понятия

Движение – мера изменения материи. Разные изменения мы называем разными видами движения. Так, изменение положения тела в пространстве относительно других тел – есть движение механическое. Механические движение мы называем просто движением. Но надо помнить, что это лишь один из многих вид изменений в Природе.

МЕХАНИКАизучает механическое движение, т.е. изменение положения тела (или его частей) относительно других тел. Вньютоновской механике скорости тел много меньше скорости света в вакууме.Релятивистская механикарассматривает движение макроскопических тел со скоростями, сравнимыми со скоростью света в вакуумес.

Основная задача механики – определить положение и скорость тела в любой момент времени. Положение тела задается его координатами в некоторойсистеме отсчета (см. ниже).

Часть 1. КинематикАизучает виды движения тел, не рассматривая причины, которые это движение обусловливают. Отвечает на вопрос:Как движется тело?

Часть 2. Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Отвечает на вопрос:Почему движение тела меняется?

Часть 3. Статика изучает условия (законы) равновесия тела или системы тел. Отвечает на вопрос:Что надо, чтобы тело не двигалось?

Часть 4. Законы сохранения задают фундаментальные инварианты во всех изменениях. Отвечают на вопрос:Что сохраняется в системе при данных в ней изменениях?

Объектом рассмотрения бывает одно тело или система тел. Например, есть разница в том, что называется импульсом одного тела и что есть импульс системы тел. Дай соответствующие определения!

Материальная точка – модель тела, обладающего массой, размерами которого в данной задаче можно пренебречь. Изучение движения произвольного тела (имеющего размеры и некоторую форму) сводится к изучению движения системы материальных точек.

Методические указания. Необходимо отметь, что в основном все, что изучается на уровне средней школы, относится лишь к механике материальной точки. Так, координаты задают положение лишь одной точки, и если имеется в виду тело, всегда имеющее некоторые размеры, то задать его положение с помощью одной тройки (в пространстве) координат нельзя! Можно лишь указать положение некоторой его точки, чаще имеется в виду центр масс (точка С) этого тела.

Кроме того, смысл термина «расстояние» (в случае когда речь идет о двух объектах) всегда сводится к расстоянию между двумя точками. Если два тела имеют формы шаров, то за расстояние между ними можно принять расстояние между точками их центров. Например, если рассматривать движение Земли вокруг Солнца, то, пренебрегая линейными размерами этих тел, за расстояние между ними принимают расстояние между точками их центров тяжести (считая Землю и Солнце симметричными по плотности шарами, получим, что центр тяжести каждого из них совпадает по положению в пространстве с его геометрическим центром). Если формы тел произвольны, то, скорее всего, расстоянием между ними будет считается кратчайшее расстояние между какими-то двумя точками их поверхностей.

В связи с этим использование модели материальной точки теоретически избавляет нас от многих неудобств и двусмысленностей. Но важно также следить за тем, насколько сильно отличаются результаты, полученные при использовании этой абстракции, от того, что есть в реальности. Иначе говоря, насколько точно модель соответствует изучаемой реальной ситуации. Необходимость введения абстракций (моделей) часто обусловлена требованием использования точного математического аппарата.

Если тело моделируется материальной точкой, то оно может двигаться одним из следующих простых¹способов:

1. прямолинейно и равномерно,

2. прямолинейной с постоянный ускорением (равнопеременно),

3. равномерно по окружности,

4. по окружности с ускорением,

5. колебание – периодическое движение или движение с повторением.

Движение тела, брошенного под углом к горизонту – составной вид движения: =1+2, т.е. равномерно по оси хи равнопеременно по осиу. Сложение этих движений дает движение по данному типу.

Если тело моделируется как АТТ, то и виды движения иные и это отражается в терминологии.

Поступательное движение - движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Траектории всех точек совершено одинаковы (полностью совмещаются), одинаковы параметры движения в любой момент времени. А потому для описания поступательного движения АТТ, достаточно описать движение любой одной его точки.

Вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемойосью вращения. У всех точек одинаковы угловые характеристики движения и различны линейные.

Для описания механического движения нужны свои средства. Их совокупность названа системой отсчета.

Учет относительности движения предполагает задание положения материальной точки по отношению к какому-то другому, произвольно выбранному телу, называемому телом отсчета.С ним связывается система координат.Система отсчета– совокупность тела отсчета, системы координат и часов. Начало отсчета времени начинается с момента «включения» часов (часы будем понимать как прибор для отсчета промежутков времени). Понятия «момент времени» и «промежуток времени» различны! Значение промежутка времени не зависит от того, по каким именно часам его засекают (в случае, если все рассматриваемые часы измеряют время в одинаковых единицах). Момент времени, напротив, полностью определяется тем, когда часы «были включены», т.е. положениемначала отсчета времени.

Описывать движение можно на разных языках:

1. на языке траектории: задаем расстояние от некоторой точки на траектории до текущего положения тела – здесь закон движения будет в форме S(t);

2. на языке координат: задаем координаты точки в выбранной системе координат (СК) – здесь закон движения будет в форме x(t), …;

3. на языке векторов: задаем радиус-вектор²точки – здесь закон движения будет в форме.

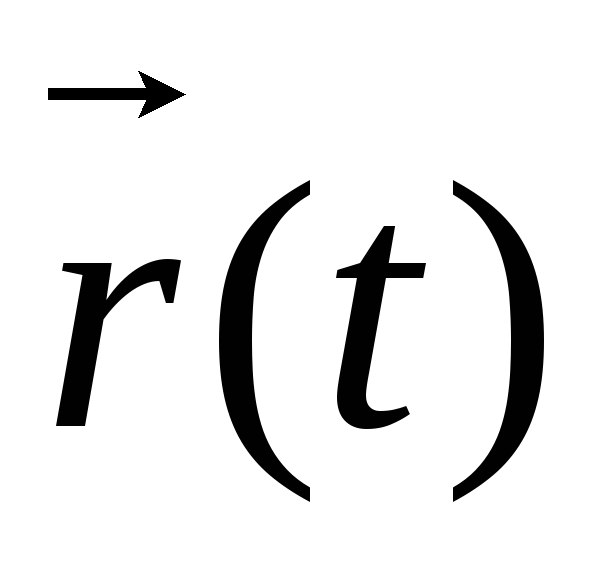Формула, выражающая зависимость координат тела (или пройденного пути) от времени, называется законом движения.

Замечание. Относительность движения выражается в том, что положение (координата или расстояние от тела отсчета), скорость и время движения рассматриваемого тела могут быть различными в разных системах отсчета. В этой связи и формула закона движения одного и того же объекта имеет различный вид в разных системах отсчета, т.е. форма записи закона движения (одного и того же вида движения) зависит от выбора положения начал отсчета времени и расстояния (а в случае задания координаты еще и от выбора положительного направления координатной оси). Чаще всего, в связи с этим, выбираемое начало отсчета времени совпадает с началом рассматриваемого движения тела, а начало координат помещают в точку начального положения этого тела.

Заметим также, что и вид движения какого-то тела может быть различным при его рассмотрении относительно разных систем отсчета.

Траектория –линия, вдоль которой движется тело.

Путь –длинатраектории (расстояние, пройденное телом вдоль траектории); скалярная неотрицательная величина. Обозначаютl, иногдаS.

Перемещение–вектор, соединяющий начальное и конечное положения тела. Обозначают.

Скорость –векторнаяфизическая величина (характеризующая изменение положения точки),равнаяпервой производной от пути (или координаты) по времени инаправленнаяпо касательной к траектории в сторону движения. Обозначают.Замечание. Скорость всегда направлена по касательной к траектории в соответствующей точке в сторону движения.

Средняя скорость – величина, равная отношению всего пути к затраченному на его прохождение времени (соответствует некоторомупромежутку времени).Мгновенная скоростьхарактеризует скорость в какой-томоментвремени.

У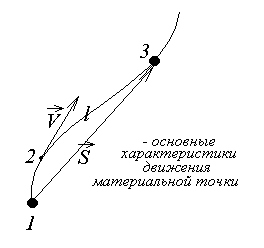скорение–векторнаявеличина, характеризующая изменение скорости (по величинеравнопервой производной от скорости по времени или второй производной от пути(или координаты)по времени;направлено как и вызывающая егосила).

Методические указания. Необходимо подчеркнуть, что в физике надо четко различать два типа величин: вектор и скаляр. Скалярная физическая величина полностью задается своей величиной (иногда с учетом знака «+» или «-»). Векторная физическая величина определяется по меньшей мере двумя характеристиками: числовым значением (числовое значение иногда называют модулем векторной величины, оно в некотором масштабе равно ДЛИНЕ изображающего его отрезка, а потому - всегда положительное число) и направлением (которое можно изобразить на рисунке или задать численно через угол, образованный этим вектором с каким-либо выделенным направлением: горизонт, вертикаль и пр.). Будем говорить, что вектор (векторная физическая величина) известен, если мы можем точно сказать про него: 1) чему он равен, И 2) как направлен. Это особенно важно иметь в виду при анализе изменения любой векторной физической величины!

При решении задач возможны следующие ситуации: 1) речь идет о векторной величине (скорости, силе, ускорении и т.д.), но рассматривается только ее значение (направление в этом случае или очевидно, или не важно, или просто не требует определения и др.). Об этом может, в частности, свидетельствовать вопрос задачи (например, «С какой скоростью v движется …», т.е. дано обозначение лишь модуля скорости. 2) Требуется найти величину как вектор: «Какова скорость v тела?» – где жирным курсивом обозначены векторные величины. 3) Нет прямого указания на тип искомого: «Какова скорость тела?». В этом случае, если позволяют данные задачи, необходимо дать полный ответ (как о векторе), исходя из определения (скорости или др.).