Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

1 Модели управления однономенклатурными запасами
1.1 Простейшая модель оптимального размера партии поставки

Эта модель позволяет определить такой размер заказываемой партии, который минимизирует расходы на организацию заказа и содержание его на складе. Экономич­ная партия поставки вычисляется при следующих допуще­ниях. Уровень запасов снижается равномерно с интенсив­ностью v (спрос). В момент, когда все запасы исчерпаны, подается заказ на поставку новой партии размером q ед. За­каз выполняется мгновенно, то есть время доставки заказа пренебрежимо мало и уровень запасов восстанавливается до максимального значения, равного q. Накладные расходы, связанные с размещением заказа и поставкой партии, не за­висят от объема партии и равны постоянной величине К. Из­держки содержания единицы товара на складе в единицу времени равны s. Срыв поставок недопустим. Пусть I(t) – уровень запасов в зависимости от времени; τ — интервал времени между поставками. Процесс изме­нения уровня запасов I показан на рисунке 4.1.


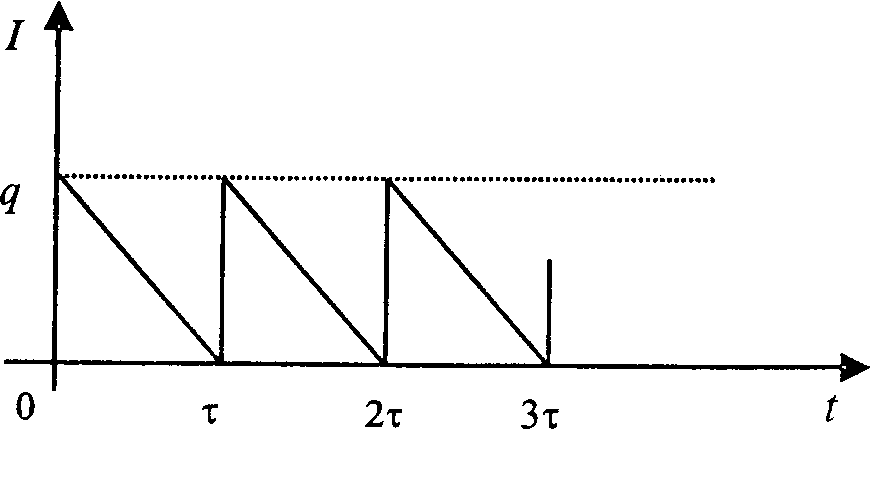
Рисунок 4.1 - Простейшая модель оптимального размера партии поставки
Таблица 4.1 – Показатели модели и формулы для их расчета

№	Показатели модели	Формулы для расчета показателей модели
1	Интервал времени между поставками
2	Об­щие затраты в единицу времени
3	Общие затраты, связанные с хранением и заказом товара
4	Оптимальный размер партии заказа (формула Уилсона)
5	Оптимальный интервал между поставками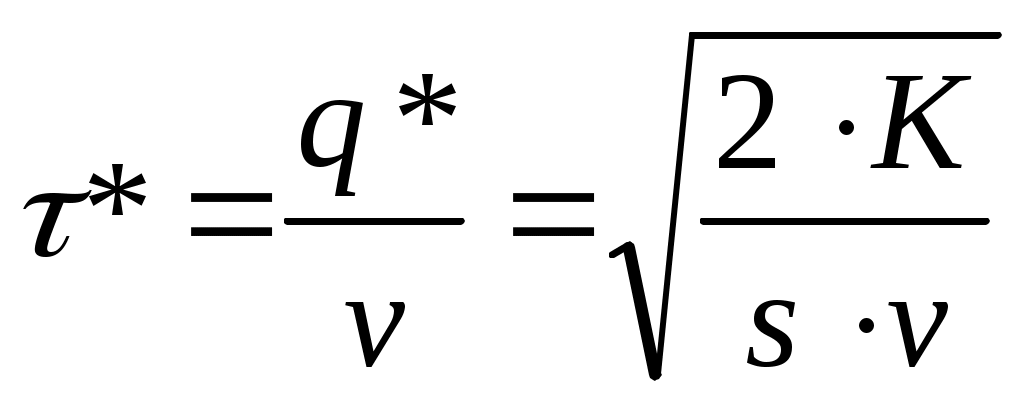
6	Оптимальный средний уровень текущего запаса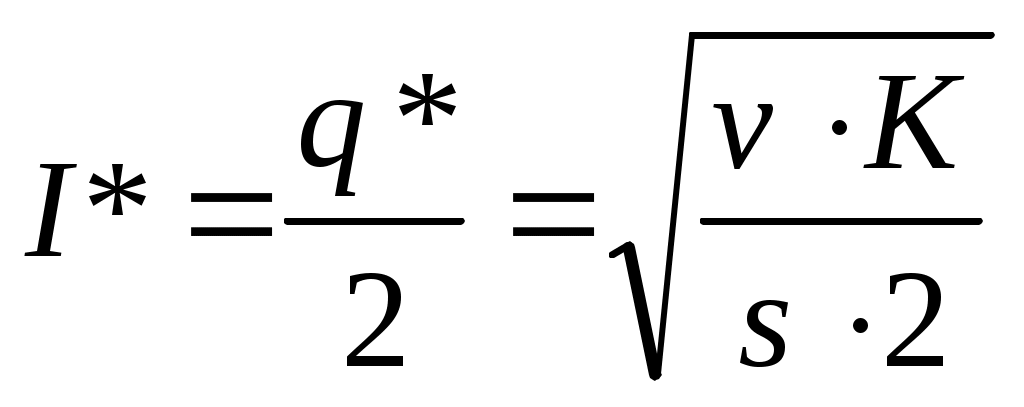
7	Потребление за плановый период	Q = vТ
8	Оптимальное число поставок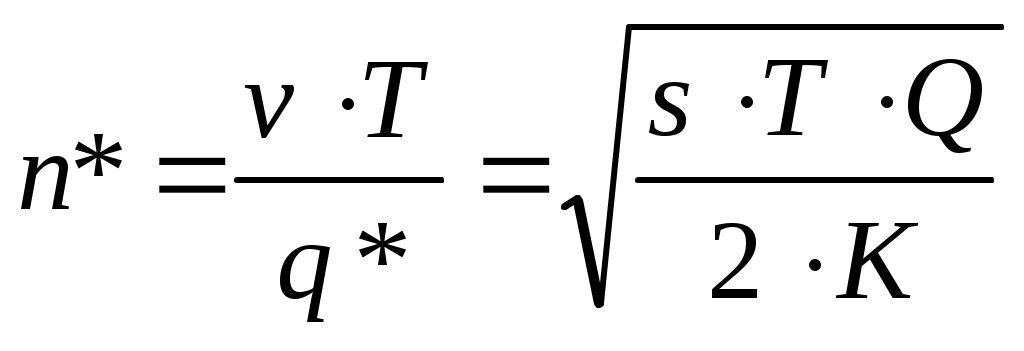
9	Суммарные затраты по формированию поставок и содер­жанию запасов в единицу времени

---

Пример решения задачи
Постановка задачи. На склад доставляются бакалейные товары партиями по 1500 т. В сутки со склада потребители забирают 50 т товара. Накладные расходы по доставке партии бакалейных товаров равны 2 млн. ден. ед. Издержки хранения 1 т товара в те­чение суток равны 100 ден. ед.

Требуется определить:

1) длительность цикла, среднесуточные накладные расхо­ды и среднесуточные издержки хранения;

2) эти же величины для размеров партии в 500 т и в 3000 т;

3) оптимальный размер заказываемой партии и расчетные характеристики работы склада в оптимальном режиме.
Решение задачи
Параметры работы склада:

ν = 50 т/сут.; К = 2 млн. ден. ед.; s = 100 ден. ед./тсут.; q= 1500 т.

1) Длительность цикла:

Среднесуточные накладные расходы:

Среднесуточные издержки хранения:



2) Аналогичные расчеты проведем для q₁ = 500 т и для q₂ = 3000 т.

3) Найдем оптимальный размер заказываемой партии по формуле Уилсона из 4-й строки таблицы 4.1:



- оптимальный средний уровень запаса по формуле (6-я строка таблицы 4.1):



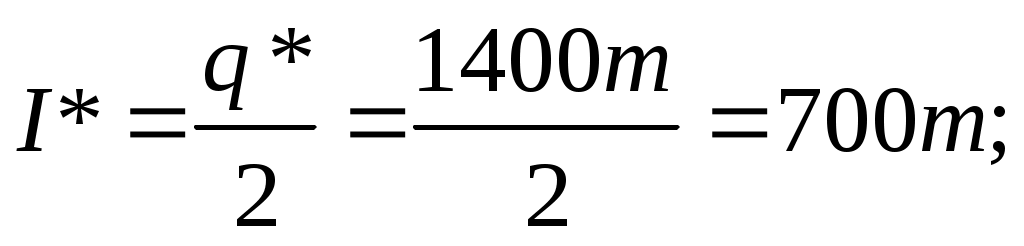
- оптимальную периодичность пополнения запасов по фор­муле (5-я строка таблицы 4.1):



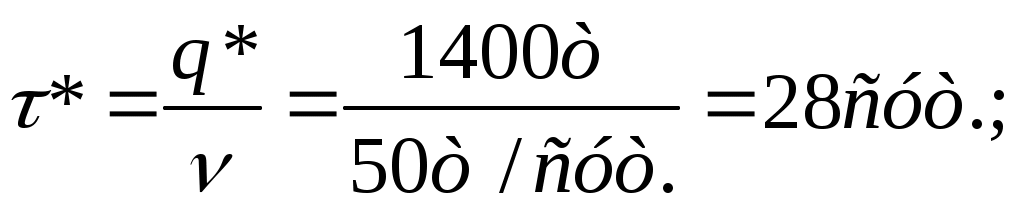
- оптимальные средние издержки хранения запасов в единицу времени по формуле из 9-й строки таблицы 4.1:


1.2 Модель с конечной интенсивностью поступления заказа

Пусть заказанная партия поступает с интенсивностью λ еди­ниц в единицу времени. Очевидно, система может работать без дефицита, если интенсивность поставок λ превосходит интенсивность потребления v. Изменение уровня запаса для рассматриваемого случая изображено на рисунке 4.2.

---

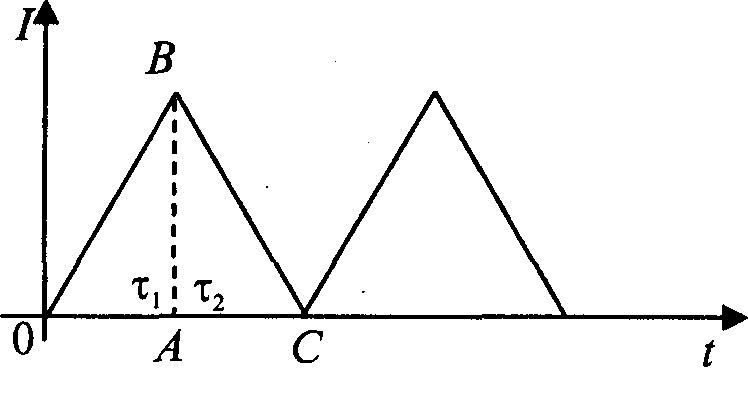
Рисунок 4.2 – Модель с конечной интенсивностью поступления заказа
В течение времени τ₁ запас одновременно и поступает, и расходуется, это время накопления запаса. В течение τ₂ за­пас только расходуется.
Таблица 4.2 – Показатели модели и формулы для их расчета

№	Показатели модели	Формулы для расчета показателей модели
1	Длина цикла
2	Максимальный наличный запас
3	Издержки системы в единицу времени
4	Величина оптимальной партии заказа
5	Оптимальный период возобновления заказа
6	Составляющие оптимального периода возобновления заказа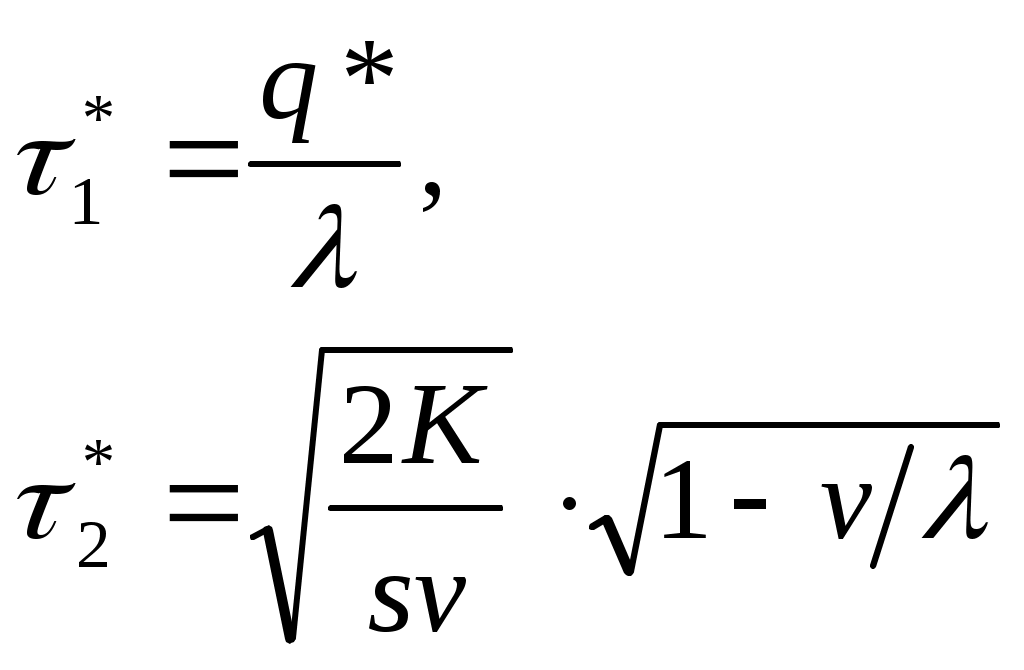
7	Минимальные издержки в единицу времени

1.3 Модель с учетом неудовлетворенных требований

Рас­смотрим случай, когда дефицит допускается, но неудовлет­воренные требования берутся на учет. При поступлении очередной партии вначале удовлетво­ряется задолженный спрос, а затем пополняется запас. Из­менение запаса в такой системе показано на рисунке 4.3.

---

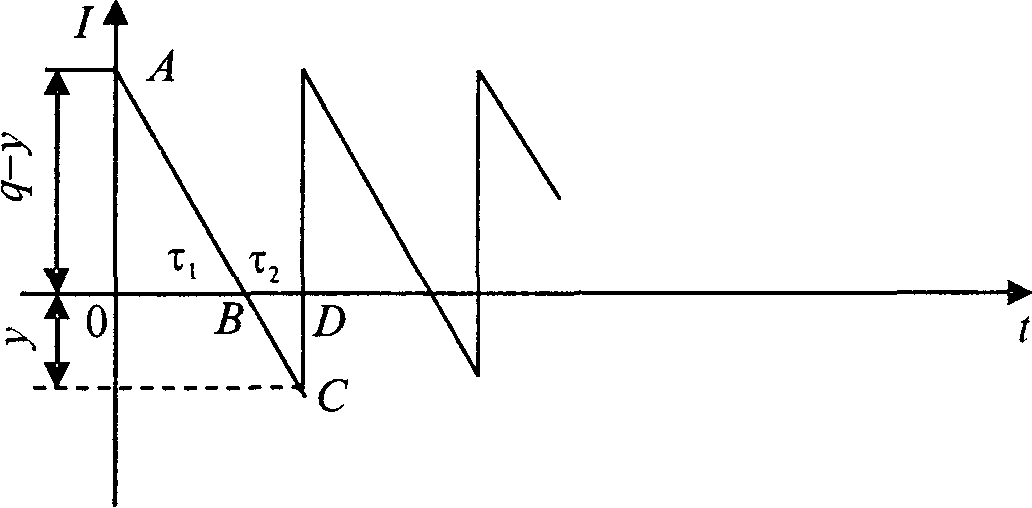
Рисунок 4.3 - Модель с учетом неудовлетворенных требований
Здесь у — максимальная величина задолженного спро­са; Y = q - у — максимальная величина наличного запаса; τ₁ — время существования наличного запаса; τ₂ — время де­фицита; d — убытки, связанные с дефицитом единицы запа­са в единицу времени.


Таблица 4.3 – Показатели модели и формулы для их расчета

№	Показатели модели	Формулы для расчета показателей модели
1	Издержки работы системы в единицу времени
2	Величина оптимальной партии заказа
3	Максимальная величина задолженного спроса
4	Минимальные издержки в единицу времени
5	Максимальная величина наличного запаса
6	Время существования наличного запаса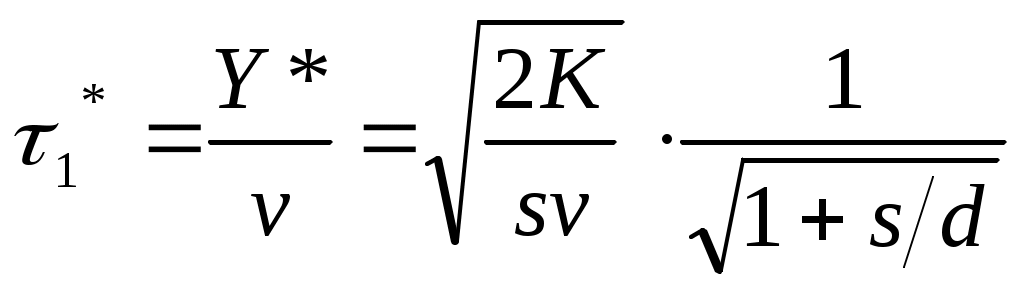
7	Время дефицита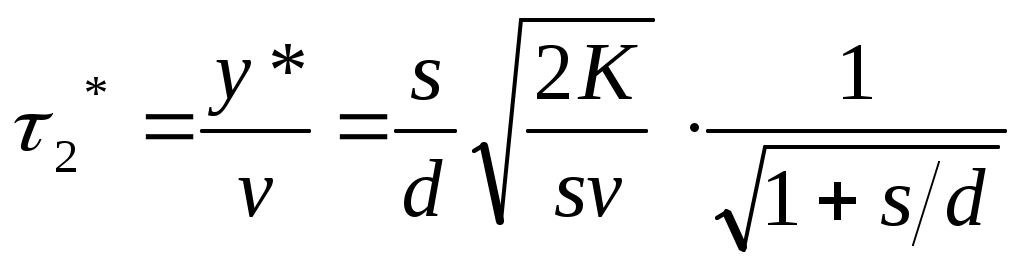
8	Оптимальный период возобновления заказа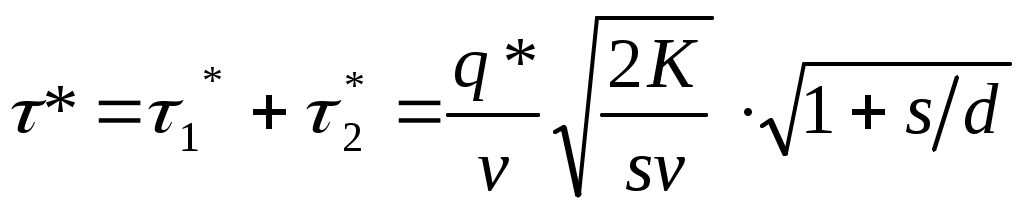

1.4 Модель с потерей неудовлетворенных требований.

Пусть неудовлетворенные требования теряются. Изменения запаса в такой системе показаны на рисунке 4.4.

---

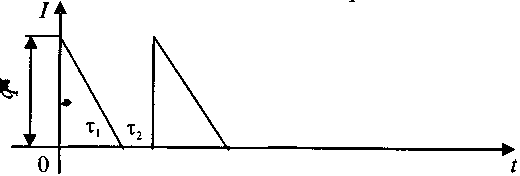
Рисунок 4.4 – Модель с потерей неудовлетворенных требований
Здесь τ₁ — время существования наличного запаса, τ₂ — время существования дефицита (запас равен 0, требования не удовлетворяются и не ставятся на учет). Из-за дефицита система несет убытки. В простейшем случае издержки дефи­цита считают пропорциональными средней величине поте­рянных требований и времени τ₂.
Таблица 4.4 – Показатели модели и формулы для их расчета

№	Показатели модели	Формулы для расчета показателей модели
1	Издержки одного цикла τ
2	Издержки работы системы в единицу времени
3	Величина оптимальной партии заказа
4	Оптимальный период возобновления заказа
5	Суммарные затраты по формированию поставок и содержанию запасов в единицу времени

1.5 Модель с определением точки заказа

В реальных ситуа­циях для обеспечения бесперебойного снабжения следует учитывать время выполнения заказа Θ, то есть заказ должен подаваться в момент, когда уровень запаса достаточен для удовлетворения потребности на время выполнения заказа. Величину наличного запаса, при которой делается заказ на пополнение, будем называть точкой размещения заказа (r). Для любого случая простейшей модели Уилсона точка раз­мещения заказа находится по формуле

---