Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Выполнение:

При построении модели множественной регрессии целесооб­разнее обратиться к инструменту Excel Регрессия, который предлагает исчерпывающую статистическую информацию о ее параметрах и качестве. Порядок работы с инструментом Регрессия определяется соответствующим окном диалога. Его можно вызвать через команду Анализ данных из контекстного меню панели Сер­вис. Диалоговое окно Регрессия предлагает пользователю определиться с набором следующих параметров (рисунок 3.19):

1) Входной интервал У — предлагает ввод ссылки на ячейки рабочего листа, которые содержат диапазон базовых данных зависимой переменной у (исследуемого показателя). В нашем примере Входной интервал Y – В2:В18;

2) Входной интервал X — предполагает ввод ссылки на ячейки рабочего листа, которые содержат диапазон базовых данных независимых переменных х₁, х₂, ..., x_k. В нашем примере Входной интервал Х – С2:D18;

3) Метки — требует установления флажка, если первая строка входного интервала содержит заголовки (названия столбцов). Если заголовки отсутствуют, то флажок устанав­ливать не нужно — Excel автоматически создаст соответству­ющие названия для данных выходного диапазона. В нашем примере – устанавливаем флажок;

4) Уровень надежности — позволяет пользователю опре­делить необходимый уровень надежности оценки выходного диапазона значений. По умолчанию Excel применяет уро­вень 95 %. Если его нужно изменить, то для данного параметра следует установить флажок и в специально открывше­еся поле ввести нужный уровень надежности. В нашем - примере флажок не устанавливаем;

5) Константа-ноль — требует установления флажка, ес­ли для уравнения регрессии не нужно рассчитывать пара­метр b (свободный член). В этом случае Excel принимает b, равным нулю. В нашем примере – флажок не устанавливаем;

6) Выходной диапазон — предполагает ввод ссылки на верхнюю левую ячейку выходного диапазона. Выходной массив значений будет зани­мать не менее семи столбцов и содержать три основных раз­дела: 1. Регрессионная статистика; 2. Дисперсионный ана­лиз; 3. Параметры (коэффициенты) регрессии и характерис­тики их статистической значимости;

7) Новый лист — применяют, если результаты анализа следует разместить на новом листе книги, начиная с ячейки А1;

8) Новая книга — используется, если результаты анализа необходимо разместить на первом листе специально откры­той для этого новой книги;

---

9) Остатки — требует установления флажка, если в це­лях проведения углубленного статистического анализа ка­чества модели в выходной диапазон, кроме трех основных разделов, необходимо включить значения отклонений фак­тических данных исследуемого показателя от соответствую­щих им точек регрессионной прямой (У фактическое - У рас­четное);

10) Стандартизированные остатки — применяют с той же целью для включения в выходной диапазон значений стандартных остатков;

11) График остатков — используется, если для статис­тического анализа необходимо построить диаграммы остат­ков для каждой независимой переменной х;

12) График подбора — предполагает формирование на ра­бочем листе диаграмм, позволяющих отследить характер связи и степень разброса наблюдаемых и предсказанных значений исследуемого показателя у с каждой независимой пе­ременной х;

13) График нормальной вероятности — требует установ­ления флажка, если пользователю необходимо получить гра­фик нормального распределения вероятности для исследуе­мого показателя.


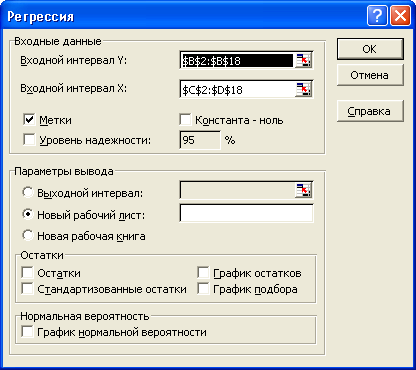
Рисунок 3.19 - Окно диалога Регрессия
Так, в первом разделе выходного массива «Регрессионная статистика» (см. ячейки А4:В8 таблицы 3.21) приведены основные статистические характерис­тики общего качества уравнения: коэффициент множествен­ной корреляции R, коэффициент детерминации R², стандартная ошибка оценки. Значе­ние R², равное 0,892, свидетельствует о том, что на основе полученного уравнения регрессии можно объяснить 89,2 % вариации объема товарооборота.

Статистические характеристики второго раздела выход­ного массива «Дисперсионный анализ» (ячейки A10:F14) по­зволяют оценить меру разброса (дисперсию) зависимой пере­менной у и остаточной вариации (дисперсии) отклонений во­круг линии регрессии. Так, значение SS_р (ячейка С12) ха­рактеризует часть дисперсии, объясненную регрессией, а SS_о (ячейка С13) — часть дисперсии, не объясненной регрес­сией из-за наличия ошибок ε. При проведении регрессионно­го анализа особый интерес представляет изменение этих зна­чений по мере введения каждого регрессора. Качество моде­ли улучшится, если после введения в нее нового фактора зна­чение объясненной части дисперсии возрастет, а не объяс­ненной — снизится.

---

В ячейках D12:D13 отражены соответственно дисперсия исходного ряда (МS_p = SS_p / df, где df = k — см. ячейку В12) и несмещенная дисперсия остаточной компоненты (MS₀ = SS₀ / df, где df = п - k - 1 — см. ячейку В13).

В ячейке F12 второго раздела выходного массива приведен уровень значимости для оцененного F. Значения F-статистики (53,72) выглядит вполне допус­тимым, поскольку уровень значимости для нее (5,210⁷) ос­тается гораздо ниже 5%-го предела, принятого для табличных F-статистик. Следова­тельно, есть основания ожидать, что F-наблюдаемое будет больше F_крит.

Оценив на основе первого и второго разделов выходного массива общее качество модели связи и убедившись в ее зна­чимости, можем перейти к третьему разделу (см. ячейки A16:G19 таблицы 3.21), который содержит детальную информа­цию о параметрах уравнения регрессии. Приведенные в ячей­ках В17:В19 значения параметров (коэффициентов) уравне­ния позволяют придать формальный вид модели, построен­ной с помощью регрессионного анализа:
у = 71650,26 – 1098,94х₁ + 255,838х₂,
где х₁ — оборачиваемость товаров, дни; х₂ - удельный вес товаров с высокими торговыми надбавками, %.
Оценить значимость каждого параметра позволяют зна­чения t-статистики (см. ячейки D17:D19). Можно использо­вать приведенный в выходном массиве уровень значимости (см. ячейки Е17:Е19): если он не превышает 0,05 (т.е. 5%-го уровня), то рассчитанные характеристики t-статистики будут больше табличного значения. Следовательно, статис­тическая значимость рассчитанных параметров уравнения весьма высока.

И, наконец, наряду с точечными значениями коэффици­ентов регрессии третий раздел выходного массива позволяет получить их интервальные оценки с доверительной вероят­ностью 95 % (см. ячейки F17:G19 таблицы 3.21):
58598,85 <b< 84701,68; -1370,81 <m₁< -827,08; 68,597 <m₂< 443,079.
На основании изложенного можно с 95%-й увереннос­тью утверждать, что параметры уравнения содержат информацию, значимую для расчета исследуемого показателя.
Таблица 3.21 - Регрессионный анализ

	А	В	С	D	E	F	G
1	ВЫВОД ИТОГОВ
2
3	Регрессионная статистика
4	Множественный R	0,94449
5	R-квадрат	0,892061
6	Нормированный R-квадрат	0,875455
7	Стандартная ошибка	767,1098
8	Наблюдения	16
9
10	Дисперсионный анализ
11		df	SS	MS	F	Значимость F
12	Регрессия	2	63223048,8	31611524,42	53,7193	5,2E-07
13	Остаток	13	7649947,59	588457,5077
14	Итого	15	70872996,4
15
16		Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
17	Y-пересечение	71650,26	6041,29087	11,86009163	2,41E-08	58598,85	84701,68
18	Оборачиваемость товаров, дни	-1098,94	125,841366	-8,732770177	8,46E-07	-1370,81	-827,08
19	Удельный вес товаров с высокими торговыми надбавками, %	255,8378	86,6708225	2,951832613	0,011232	68,59687	443,0787

---

---

4 Модели управления товарными запасами

Формируемые навыки и умения:

- освоение методики решения моделей управления однономенклатурными запасами; - освоение методики решения моделей многономенклатурными запасами.

Теоретическая поддержка
Одним из важнейших этапов планирования работы любой производствен­ной или торговой единицы является определение оптимального уровня запасов сы­рья, полуфабрикатов, товаров или продукции.

Под запасом понимается годный к употреблению, но не используемый в на­стоящее время ресурс. Создание и хранение запасов обуславливает наличие различ­ного рода издержек, таких как: издержки, связанные с приобретением партии, затраты на оформление заказа, издержки хранения запаса, издержки, связанные с отсутствием запасов, и т. д.

В целом управление запасами включает задачи анализа, прогноза, планирования и нормирования. Перечисленные задачи можно решать с помощью методов и моделей теории управ­ления запасами. Целью теории является разработка методов и моделей выбора таких параметров управления, при которых дости­гается оптимум (минимум или максимум) какого-либо критерия оптимальности, например минимум затрат, максимум прибыли, минимум времени и др.

Одним из важнейших направлений управления запасами является их оптими­зация. Под оптимальным запасом следует понимать минимально необходимый размер товарного запаса, обеспечивающий бесперебойное обеспечение товарами в соответствии со спросом при минимальном уровне затрат на приобретение и хране­ние, а также минимальными потерями от дефицита.

Решение задач определения оптимальных параметров управления запасами зависит от:

- характера спроса на товарную продукцию (детерминированный или вероят­ностный);

- времени пополнения запаса (мгновенное или равномерное);

- числа видов продукции (однономенклатурные и многономенклатурные модели).

Многономенклатурные модели могут иметь такие ограничения, как дефицит складских площадей, габаритов упаковки и т.п. В этих случаях в параметры моделей, в частности в размеры оптимальных партий, необходимо внести определённые по­правки.

---