Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 818
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Модель общей задачи линейного программирования
2 Транспортные задачи в моделировании
3 Экономико-статистическое моделирование и прогнозирование средствами MS Excel
4 Модели управления товарными запасами
5 Системы массового обслуживания
6 Модели сетевого планирования и управления
7 Применение элементов теории игр при принятии управленческих решений
, (4.1)
где [.] — целая часть числа (.).
Для обеспечения бездефицитной работы необходимо иметь минимальный начальный запас I0, величина которого рассчитывается по формуле
I0 = Θv. (4.2)
Пусть I — фактический начальный запас. Для непрерывной работы необходимо, чтобы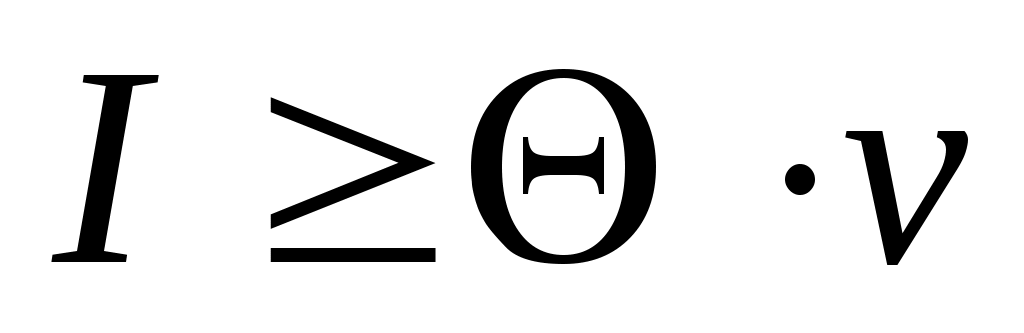 . Время потребления начального запаса равно I/v. Чтобы заказанная партия была доставлена не позже полного расхода начального запаса, ее нужно разместить в момент
. Время потребления начального запаса равно I/v. Чтобы заказанная партия была доставлена не позже полного расхода начального запаса, ее нужно разместить в момент
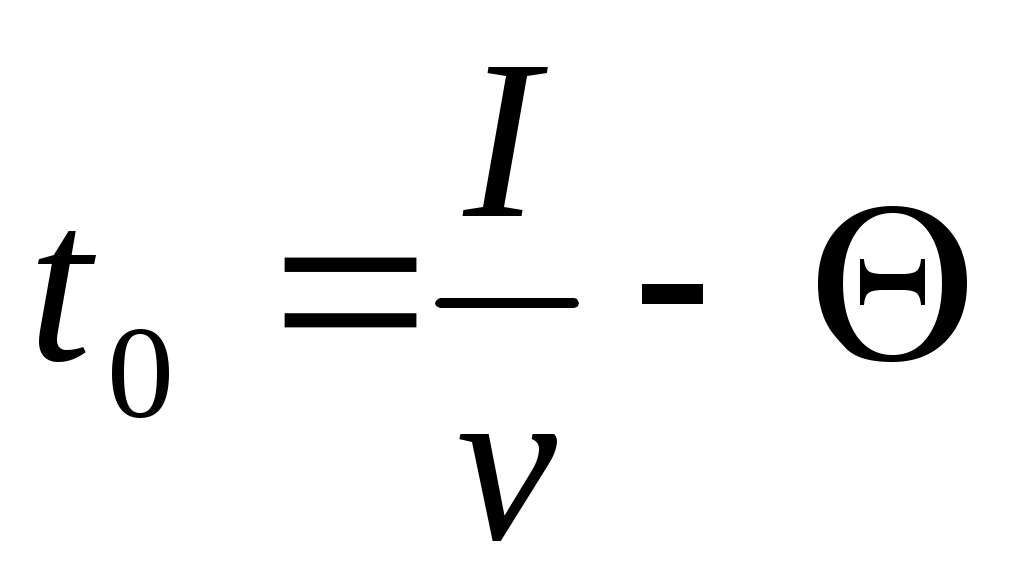 . (4.3)
. (4.3)
В общем случае заказы нужно размещать в моменты
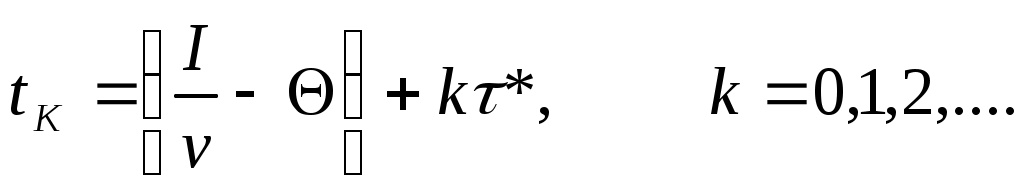 (4.4)
(4.4)
В системе с конечной интенсивностью поступления заказа при определении оптимальной точки заказа рассматриваются два случая:
1) если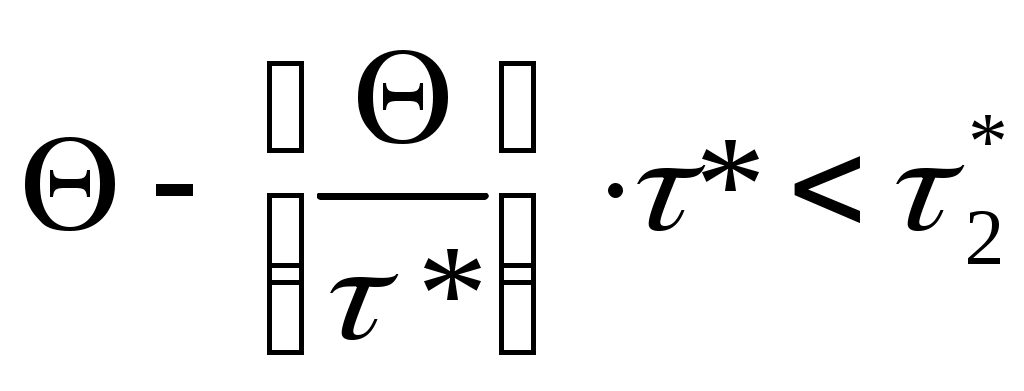 , то
, то 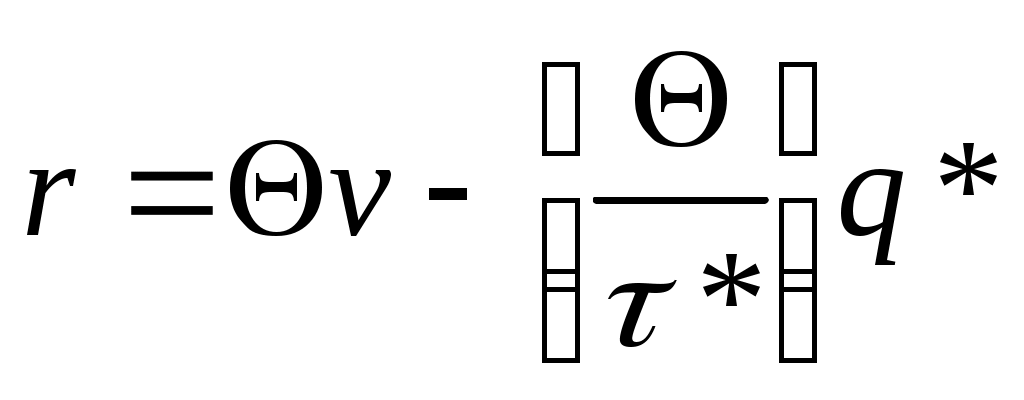 ;
;
2) если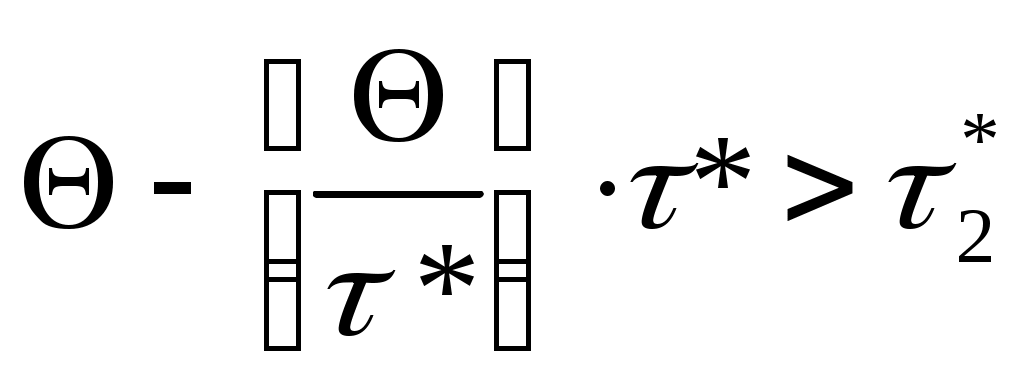 , то
, то  .
.
Для системы с учетом неудовлетворенных требований точка заказа определяется по формуле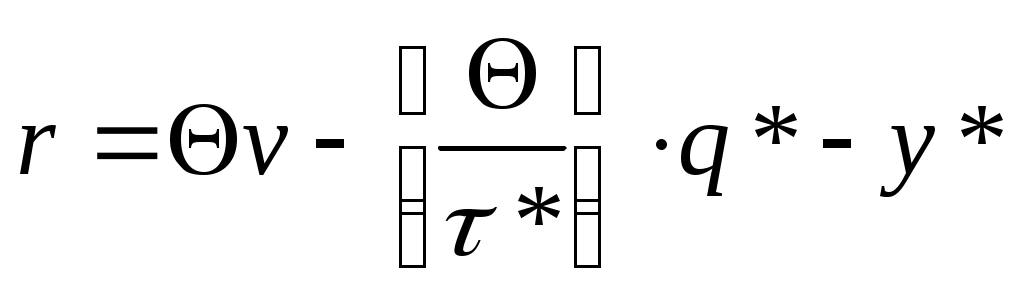 и может быть отрицательной величиной. То есть заявки на пополнение запаса должны посылаться, когда величина дефицита составляет |r|.
и может быть отрицательной величиной. То есть заявки на пополнение запаса должны посылаться, когда величина дефицита составляет |r|.
Задачи для самостоятельного решения
Задача 1
Годовая потребность мясокомбината в сырье составляет 4000 т, затраты на хранение 1 т в год — 4 ден. ед. Затраты на подготовительно-заключительные операции, не зависящие от величины поставляемой партии и связанные с каждой поставкой, равны 80 ден. ед.
Требуется определить оптимальные параметры системы, а также сравнить полученные затраты с затратами в случае отклонений от оптимальной партии в любом направлении в два раза.
Задача 2
Жидкие продукты нескольких видов разливаются в пакеты на одной линии упаковки. Затраты на подготовительно-заключительные операции составляют 700 ден. ед., потребность в продуктах составляет 140 тыс. л в месяц, стоимость хранения 1 л в течение месяца – 4 ден. ед. Определить оптимальные параметры системы. Сравнить минимальные затраты с затратами при действующей системе разлива одного продукта в течение трех дней.
Задача 3
Потребность хлебозавода в сырье составляет 32000 т в год. Издержки размещения заказа — 50 ден. ед., издержки содержания 1 т сырья в год равны 5 ден. ед. Среднее время реализации заказа — 10 дней.
Определить оптимальную партию поставки, периодичность возобновления поставок, затраты по формированию поставок, точку размещения заказа, минимальный начальный запас и моменты повторения заказов.
Задача 4
Фабрика выпускает партиями пять различных полуфабрикатов. Интенсивность потребления каждого вида составляет 76 т в месяц. При переходе от выпуска одного вида полуфабриката к другому нужно проводить переналадки оборудования, что связанно с затратами в 81 ден. ед. независимо от выпускаемых полуфабрикатов. Содержание 1 т полуфабрикатов обходится в 38 ден. ед. в месяц. Производительность фабрики — 400 т в месяц. Время реализации заказа (от подачи заявки до выхода готовой продукции) составляет 3 дня.
Определить оптимальный размер партии выпуска каждого вида полуфабрикатов, периодичность повторения заказов, точку их размещения и среднемесячные издержки, связанные с переналадками и содержанием готовой продукции, если дефицит не допускается.
Задача 5
Годовая потребность молочного комбината в молоке — 900 т. Затраты, связанные с содержанием 1 тонны молока, составляют 40 ден. ед. в год, а затраты, связанные с оформлением каждого заказа
, — 500 ден. ед. Согласно торговому договору сельскохозяйственные предприятия должны заказанное молочным комбинатом молоко поставлять по частям с интенсивностью 150 т в месяц, пока не используется вся партия. Если в момент обращения комбината в совхозы нет молока, то требование ставится на учет и удовлетворяется по мере новых поступлений. Издержки дефицита, включающие затраты, связанные с учетом неудовлетворенных требований, составляют в год 40 ден. ед./шт.
Определить оптимальную партию поставки, оптимальный интервал возобновления заказа и среднегодовые издержки.
Задача 6
Спрос на продукцию кондитерской фабрики составляет 6200 т в год. Стоимость хранения составляет 496 ден. ед. за тонну в год. Издержки размещения заказа равны 1296 ден. ед. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 3600 ден. ед. за нехватку тонны продукции в течение года.
Найти оптимальную партию поставки, максимальную величину задолженного спроса, интервал возобновления поставки, точку размещения заказа (время доставки — 0,5 месяца) и годовые потери функционирования системы.
2 Модели управления многономенклатурными запасами
Складские системы предприятий промышленности или оптовой торговли содержат от нескольких десятков до нескольких тысяч номенклатур. Следовательно, возникает необходимость рассмотрения задач управления многономенклатурными запасами.
Раздельная оптимизация. Допустим, что запасы поступают из разных источников, т.е. имеет место полное разделение заказов. Каждая продукция имеет свою интенсивность спроса vi, свою стоимость размещения заказа Кi, свои затраты на хранение si, таких видов продукции N. Заказ пополняется мгновенно. Все виды продукции хранятся на одном складе ограниченной площадьюS, и площадь склада – f.
Ставится задача найти оптимальные размеры заказа для каждой продукции с учетом того, что все запасы поместятся на складе ограниченной площади, если известна площадь fi, занимаемая каждым видом продукции qi.
Полное совмещение заказов. При пополнении запасов из одного источника часто несколько заказов объединяются. Период размещения заказа по всем номенклатурам будет общим.
Пример решения задачи
Постановка задачи. Четыре различных вида продукции хранятся на складе с целью непрерывного использования в технологическом процессе. Дефицит не допускается, и запас должен пополняться мгновенно после поступления заказа. Обозначим: fi — площадь, необходимая для хранения единицы продукции i-го вида; Кi — затраты на оформление заказа на партию продукции i-гo вида; νi — интенсивность спроса на продукцию i-гo вида в единицу времени; si — затраты на хранение i-гo вида продукции в единицу времени.
Числовые данные представлены в таблице 4.5.
Таблица 4.5 – Исходные данные задачи
Требуется:
1) найти оптимальные размеры заказов для четырёх видов продукции, если общая площадь складских помещений составляет 200 м2. Рассчитать издержки работы системы управления запасами. Учесть, что все четыре вида продукции поступают на склад от разных поставщиков (раздельная оптимизация);
2) если продукция поступает из одного источника (полное совмещение заказов), издержки размещения заказов в этом случае равны средним издержкам индивидуальных издержек заказывания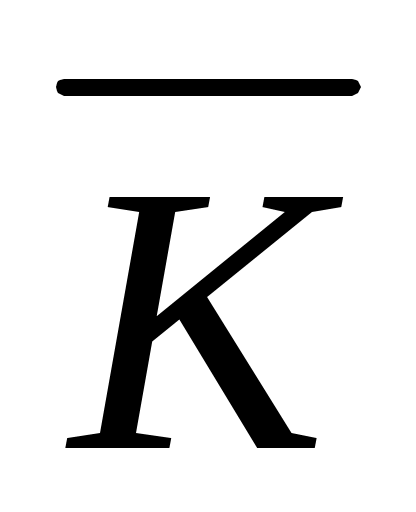 плюс 15 % стоимости организации заказа по каждому продукту;
плюс 15 % стоимости организации заказа по каждому продукту;
3) сравнить полученные результаты с действующей системой поставок — один раз в квартал с индивидуальным подходом к каждому продукту без учета ограничений на складские площади.
Решение задачи
1 Раздельная оптимизация без ограничений на складские площади
Обозначим qi - размер заказа на продукцию i-гo вида. Тогда ограничения на потребность в складской площади принимают вид:
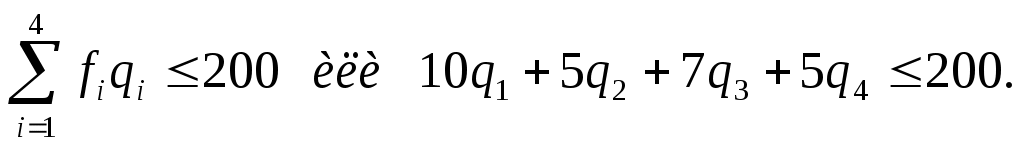
Допустим, что запасы всех видов продукции пополняются одномоментно, т.е. в это время запас и занятая им площадь оказывается максимальными.
Таким образом, рассматриваемая задача минимизации суммарных издержек системы управления запасами имеет вид
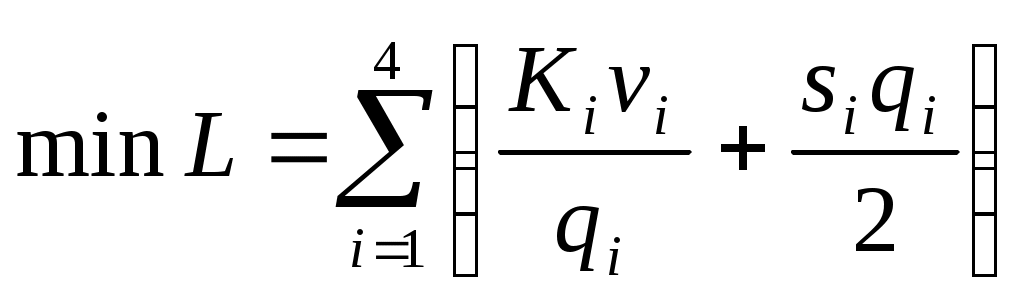 , (4.5)
, (4.5)
при ограничении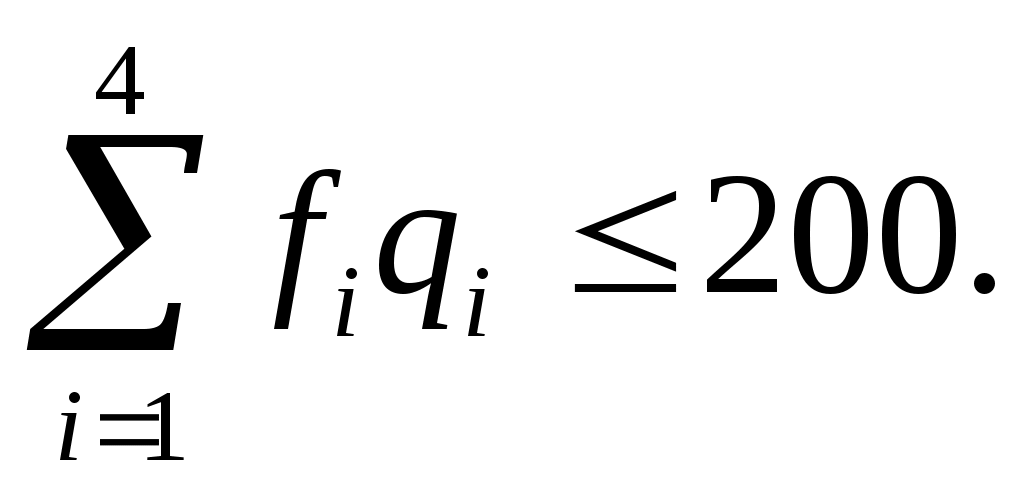 (4.6)
(4.6)
На рабочем листе в ячейках А2:Е6 строим таблицу 4.6 с исходными данными.
Таблица 4.6 - Исходные данные для решения задачи
Найдем оптимальные размеры поставок (qi*) при отсутствии ограничений по формуле Уилсона:
где [.] — целая часть числа (.).
Для обеспечения бездефицитной работы необходимо иметь минимальный начальный запас I0, величина которого рассчитывается по формуле
I0 = Θv. (4.2)
Пусть I — фактический начальный запас. Для непрерывной работы необходимо, чтобы
В общем случае заказы нужно размещать в моменты
В системе с конечной интенсивностью поступления заказа при определении оптимальной точки заказа рассматриваются два случая:
1) если
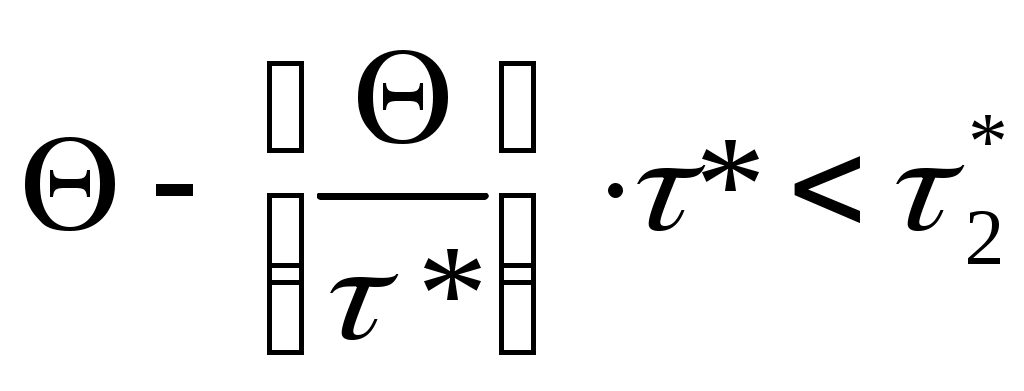 , то
, то 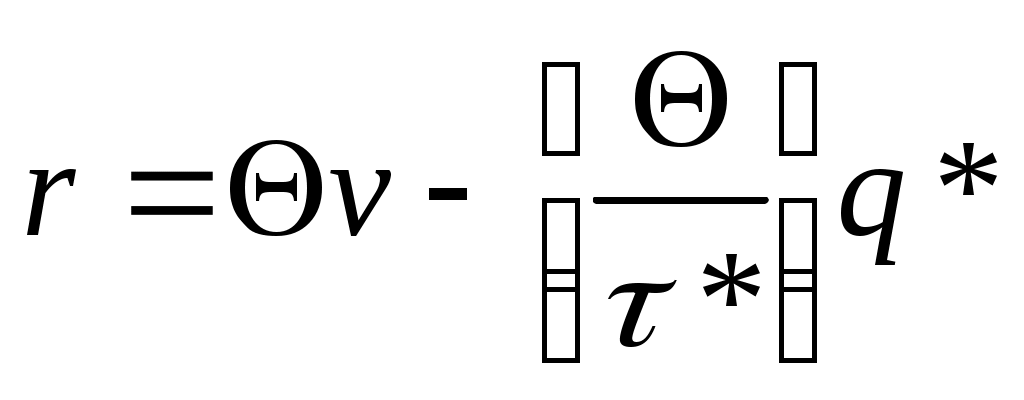 ;
;2) если
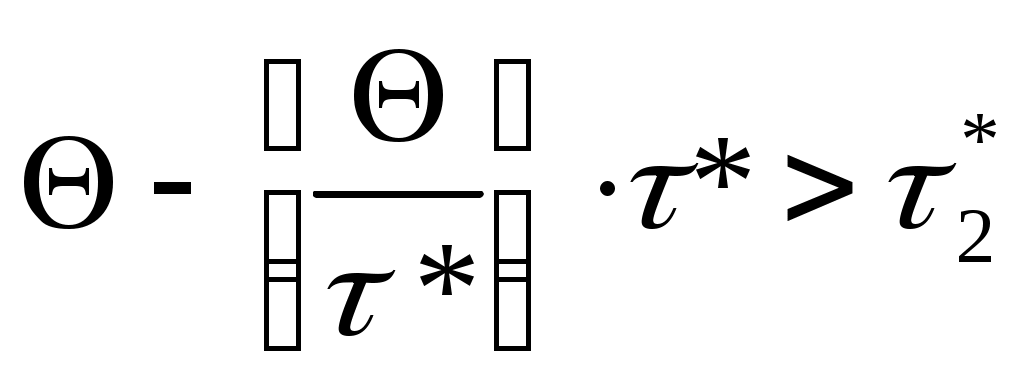 , то
, то  .
.Для системы с учетом неудовлетворенных требований точка заказа определяется по формуле
 и может быть отрицательной величиной. То есть заявки на пополнение запаса должны посылаться, когда величина дефицита составляет |r|.
и может быть отрицательной величиной. То есть заявки на пополнение запаса должны посылаться, когда величина дефицита составляет |r|.Задачи для самостоятельного решения
Задача 1
Годовая потребность мясокомбината в сырье составляет 4000 т, затраты на хранение 1 т в год — 4 ден. ед. Затраты на подготовительно-заключительные операции, не зависящие от величины поставляемой партии и связанные с каждой поставкой, равны 80 ден. ед.
Требуется определить оптимальные параметры системы, а также сравнить полученные затраты с затратами в случае отклонений от оптимальной партии в любом направлении в два раза.
Задача 2
Жидкие продукты нескольких видов разливаются в пакеты на одной линии упаковки. Затраты на подготовительно-заключительные операции составляют 700 ден. ед., потребность в продуктах составляет 140 тыс. л в месяц, стоимость хранения 1 л в течение месяца – 4 ден. ед. Определить оптимальные параметры системы. Сравнить минимальные затраты с затратами при действующей системе разлива одного продукта в течение трех дней.
Задача 3
Потребность хлебозавода в сырье составляет 32000 т в год. Издержки размещения заказа — 50 ден. ед., издержки содержания 1 т сырья в год равны 5 ден. ед. Среднее время реализации заказа — 10 дней.
Определить оптимальную партию поставки, периодичность возобновления поставок, затраты по формированию поставок, точку размещения заказа, минимальный начальный запас и моменты повторения заказов.
Задача 4
Фабрика выпускает партиями пять различных полуфабрикатов. Интенсивность потребления каждого вида составляет 76 т в месяц. При переходе от выпуска одного вида полуфабриката к другому нужно проводить переналадки оборудования, что связанно с затратами в 81 ден. ед. независимо от выпускаемых полуфабрикатов. Содержание 1 т полуфабрикатов обходится в 38 ден. ед. в месяц. Производительность фабрики — 400 т в месяц. Время реализации заказа (от подачи заявки до выхода готовой продукции) составляет 3 дня.
Определить оптимальный размер партии выпуска каждого вида полуфабрикатов, периодичность повторения заказов, точку их размещения и среднемесячные издержки, связанные с переналадками и содержанием готовой продукции, если дефицит не допускается.
Задача 5
Годовая потребность молочного комбината в молоке — 900 т. Затраты, связанные с содержанием 1 тонны молока, составляют 40 ден. ед. в год, а затраты, связанные с оформлением каждого заказа
, — 500 ден. ед. Согласно торговому договору сельскохозяйственные предприятия должны заказанное молочным комбинатом молоко поставлять по частям с интенсивностью 150 т в месяц, пока не используется вся партия. Если в момент обращения комбината в совхозы нет молока, то требование ставится на учет и удовлетворяется по мере новых поступлений. Издержки дефицита, включающие затраты, связанные с учетом неудовлетворенных требований, составляют в год 40 ден. ед./шт.
Определить оптимальную партию поставки, оптимальный интервал возобновления заказа и среднегодовые издержки.
Задача 6
Спрос на продукцию кондитерской фабрики составляет 6200 т в год. Стоимость хранения составляет 496 ден. ед. за тонну в год. Издержки размещения заказа равны 1296 ден. ед. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 3600 ден. ед. за нехватку тонны продукции в течение года.
Найти оптимальную партию поставки, максимальную величину задолженного спроса, интервал возобновления поставки, точку размещения заказа (время доставки — 0,5 месяца) и годовые потери функционирования системы.
2 Модели управления многономенклатурными запасами
Складские системы предприятий промышленности или оптовой торговли содержат от нескольких десятков до нескольких тысяч номенклатур. Следовательно, возникает необходимость рассмотрения задач управления многономенклатурными запасами.
Раздельная оптимизация. Допустим, что запасы поступают из разных источников, т.е. имеет место полное разделение заказов. Каждая продукция имеет свою интенсивность спроса vi, свою стоимость размещения заказа Кi, свои затраты на хранение si, таких видов продукции N. Заказ пополняется мгновенно. Все виды продукции хранятся на одном складе ограниченной площадьюS, и площадь склада – f.
Ставится задача найти оптимальные размеры заказа для каждой продукции с учетом того, что все запасы поместятся на складе ограниченной площади, если известна площадь fi, занимаемая каждым видом продукции qi.
Полное совмещение заказов. При пополнении запасов из одного источника часто несколько заказов объединяются. Период размещения заказа по всем номенклатурам будет общим.
Пример решения задачи
Постановка задачи. Четыре различных вида продукции хранятся на складе с целью непрерывного использования в технологическом процессе. Дефицит не допускается, и запас должен пополняться мгновенно после поступления заказа. Обозначим: fi — площадь, необходимая для хранения единицы продукции i-го вида; Кi — затраты на оформление заказа на партию продукции i-гo вида; νi — интенсивность спроса на продукцию i-гo вида в единицу времени; si — затраты на хранение i-гo вида продукции в единицу времени.
Числовые данные представлены в таблице 4.5.
Таблица 4.5 – Исходные данные задачи
-
Вид продукции (I)
Кi, ден. ед.
νi , ед.
si, ден. ед.
fi, м2
1
100
10
0,1
10
2
50
20
0,2
5
3
90
5
0,2
7
4
20
10
0,1
5
Требуется:
1) найти оптимальные размеры заказов для четырёх видов продукции, если общая площадь складских помещений составляет 200 м2. Рассчитать издержки работы системы управления запасами. Учесть, что все четыре вида продукции поступают на склад от разных поставщиков (раздельная оптимизация);
2) если продукция поступает из одного источника (полное совмещение заказов), издержки размещения заказов в этом случае равны средним издержкам индивидуальных издержек заказывания
3) сравнить полученные результаты с действующей системой поставок — один раз в квартал с индивидуальным подходом к каждому продукту без учета ограничений на складские площади.
Решение задачи
1 Раздельная оптимизация без ограничений на складские площади
Обозначим qi - размер заказа на продукцию i-гo вида. Тогда ограничения на потребность в складской площади принимают вид:
Допустим, что запасы всех видов продукции пополняются одномоментно, т.е. в это время запас и занятая им площадь оказывается максимальными.
Таким образом, рассматриваемая задача минимизации суммарных издержек системы управления запасами имеет вид
при ограничении
На рабочем листе в ячейках А2:Е6 строим таблицу 4.6 с исходными данными.
Таблица 4.6 - Исходные данные для решения задачи
-
А
В
С
D
E
2
I
vi
Ki
si
fi
3
1
10
100
0,1
10
4
2
20
50
0,2
5
5
3
5
90
0,2
7
6
4
10
20
0,1
5
Найдем оптимальные размеры поставок (qi*) при отсутствии ограничений по формуле Уилсона: