Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 811
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Модель общей задачи линейного программирования
2 Транспортные задачи в моделировании
3 Экономико-статистическое моделирование и прогнозирование средствами MS Excel
4 Модели управления товарными запасами
5 Системы массового обслуживания
6 Модели сетевого планирования и управления
7 Применение элементов теории игр при принятии управленческих решений
aij, который он получит, используя стратегию Аi, не зная, какое из состояний Пj природа действительно реализует. То есть элементы матрицы рисков определяются по формуле
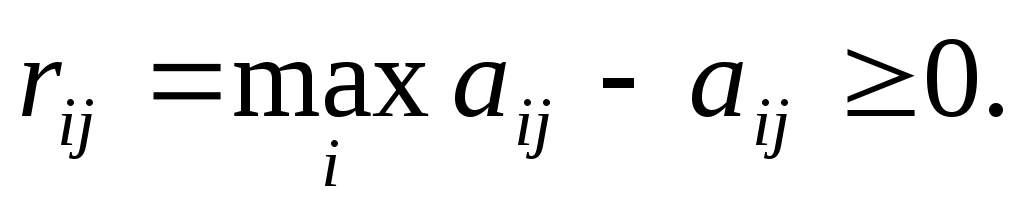(7.8)
Применяется две группы критериев — использующих и не использующих априорные вероятности qj состояний природы. К первой группе относятся критерии Байеса и Лапласа.
В качестве оптимальной по критерию Байеса принимается чистая стратегия Аi, при которой максимизируется средний выигрыш статистика
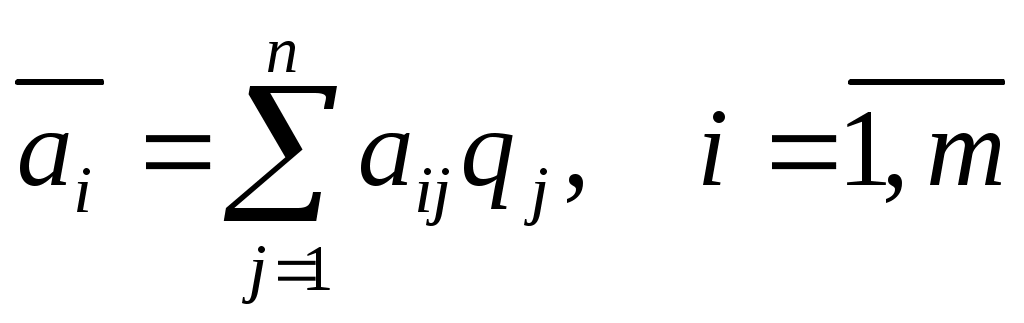, (7.9)
то есть обеспечивается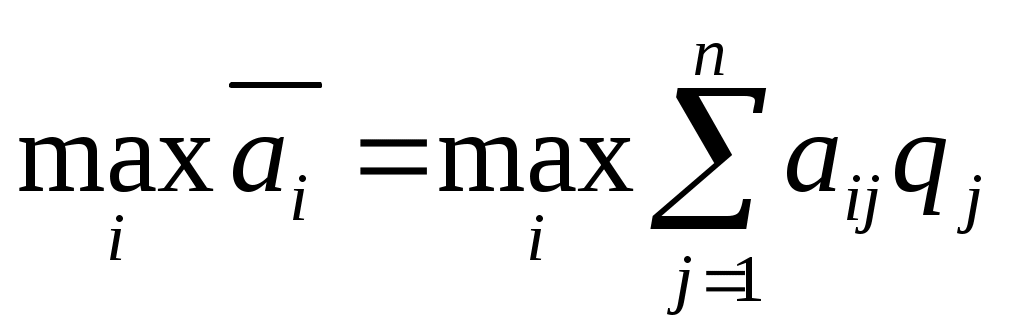
. (7.10)
Если статистику представляются в равной мере правдоподобными все состояния Пj природы, то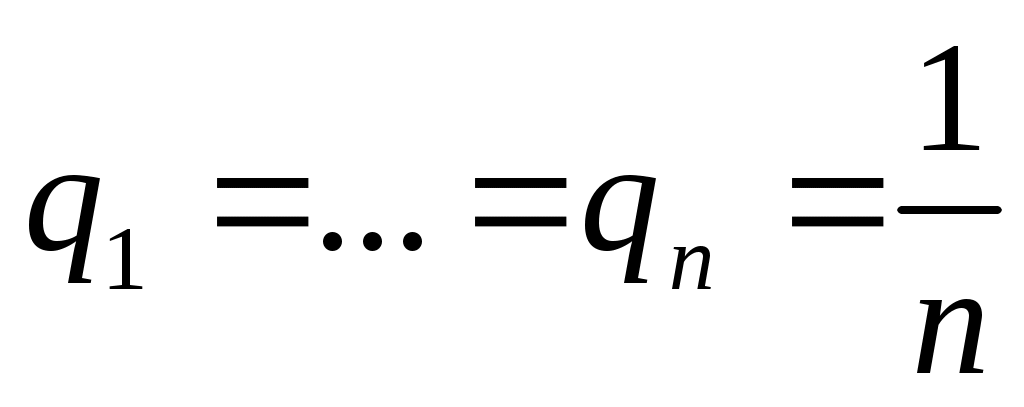
и оптимальной по критерию Лапласа считается чистая стратегия Аi, обеспечивающая
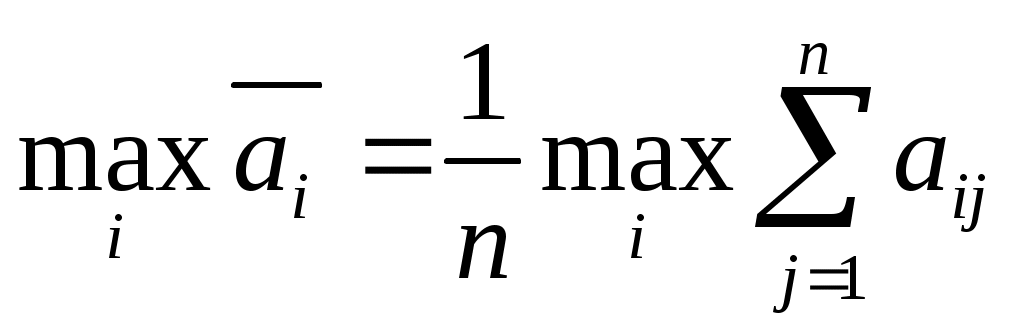. (7.11)
Ко второй группе критериев, применяемых при неизвестных априорных вероятностях состояний природы, относятся критерии Вальда, Сэвиджа и Гурвица.
Оптимальной по критерию Вальда считается чистая стратегия Аi, при которой наименьший выигрыш статистика будет максимальным, то есть ему обеспечивается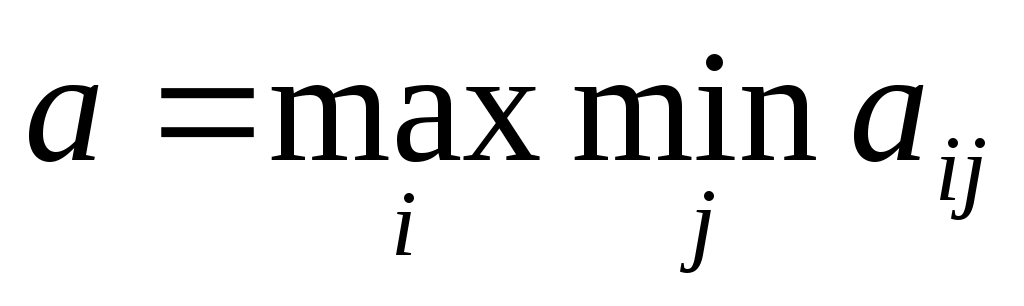
.
Для смешанных стратегий критерий Вальда формулируется так: оптимальной считается та смешанная стратегия, при которой минимальный средний выигрыш статистика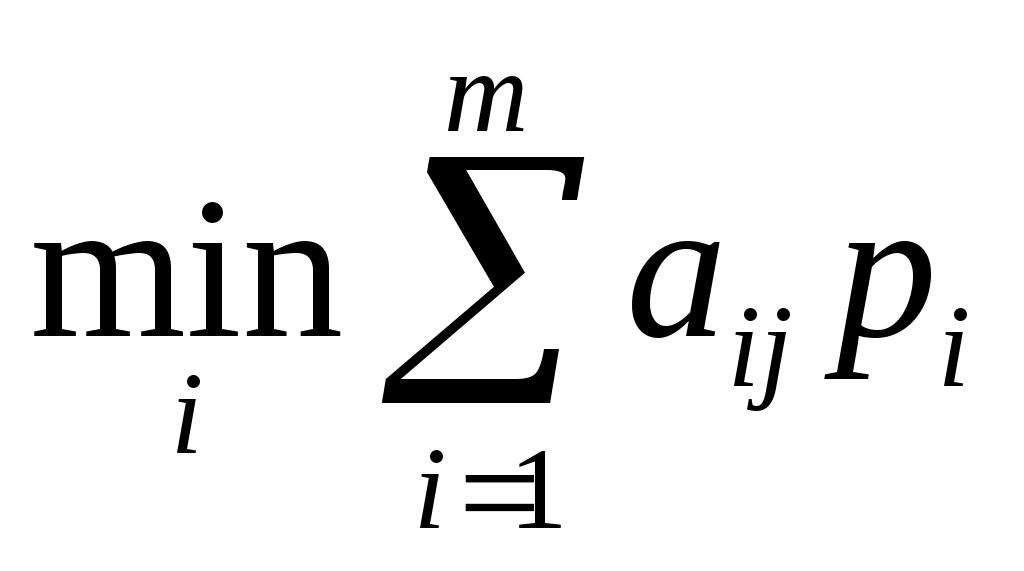
будет максимальным, то есть стратегия р*, найденная из условия 
.
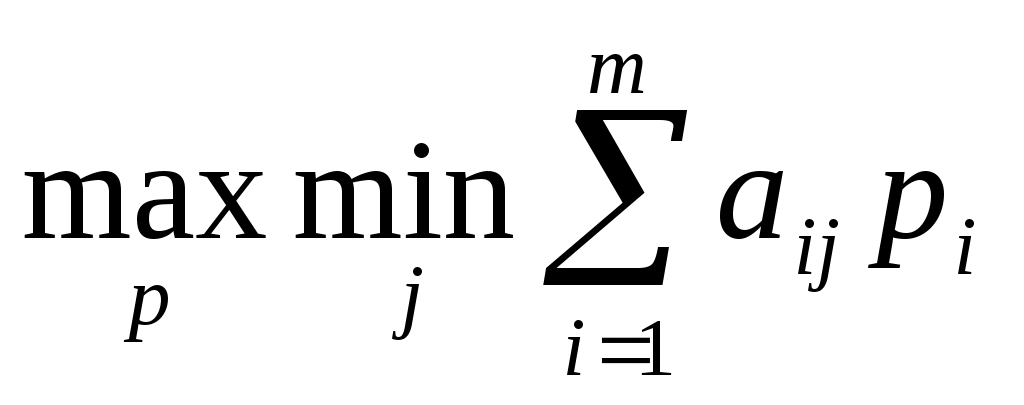Оптимальной по критерию Сэвиджа считается та чистая стратегия Аi, при которой минимизируется величина ri максимального риска, то есть обеспечивается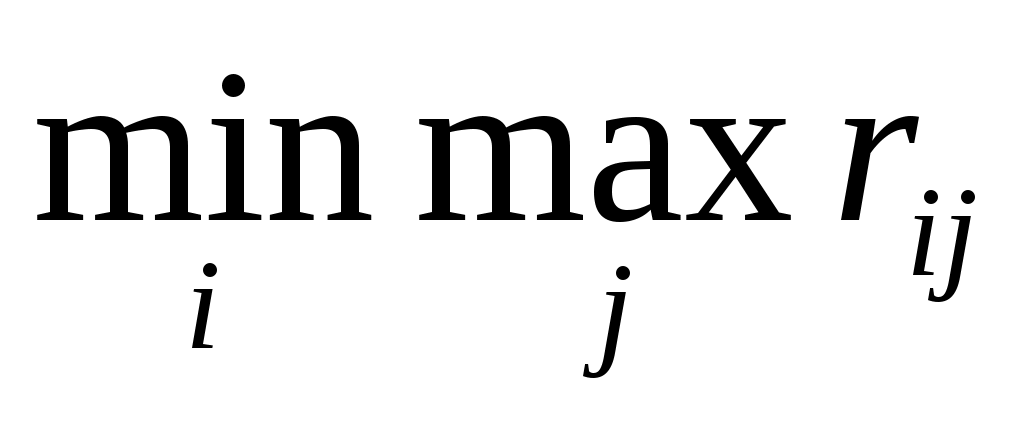
.
Для смешанных стратегий критерий Сэвиджа формулируется так: оптимальной считается та смешанная стратегия, при которой максимальный средний риск статистика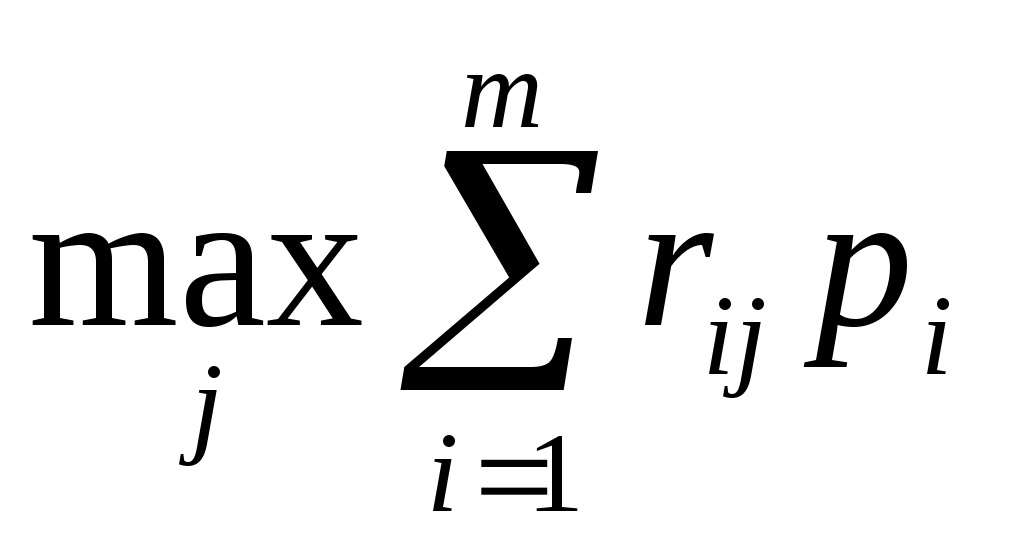
минимизируется, то есть стратегия р*, найденная из условия 
.
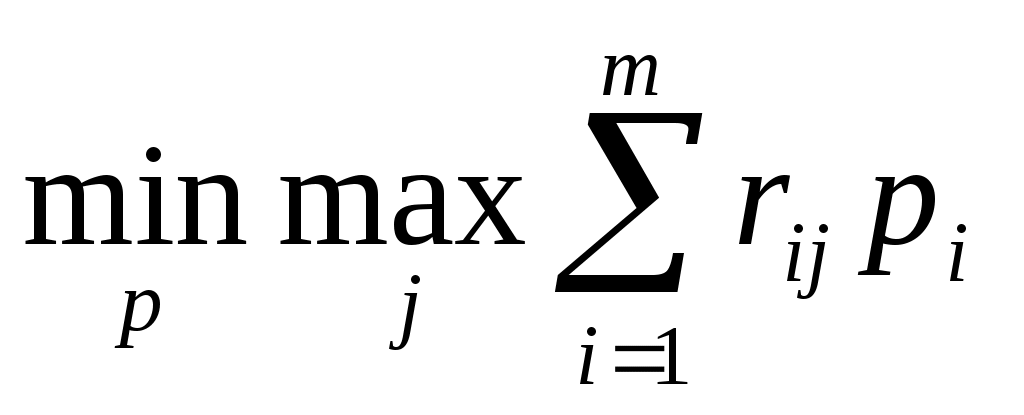Оптимальной по критерию Гурвица считается чистая стратегия Аi, найденная из условия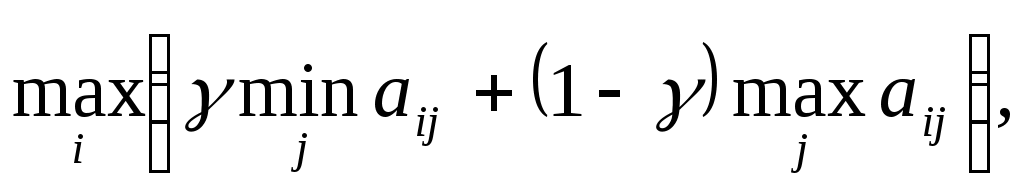
где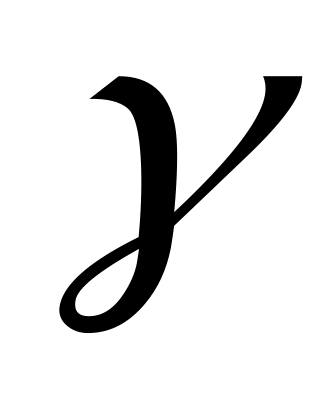
принадлежит интервалу (0; 1) и выбирается из субъективных соображений. При 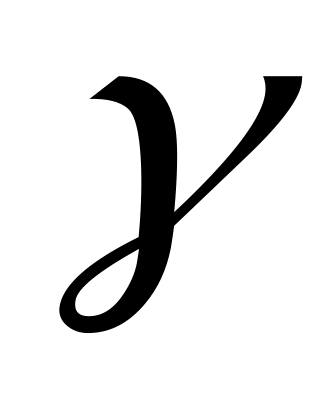= 1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда, а при 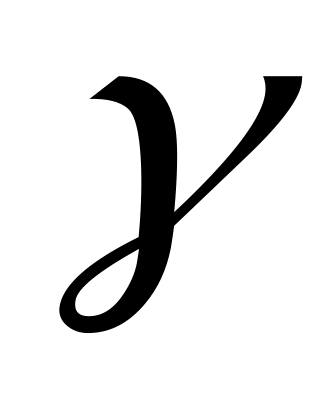= 0 — в критерий крайнего оптимизма.
Пример решения задачи
Постановка задачи. Кафетерий «Мечта» реализует кондитерские изделия собственного изготовления. Спрос на пирожные может составить 100, 120, 140 или 160 шт. с вероятностью 0,2; 0,3; 0,4; 0,1 соответственно. Затраты на производство одного пирожного составляют 70 ден. ед., а цена реализации — 100 ден. ед. Если пирожные не продаются в течение 36 ч, они портятся и магазин несет убытки.
Какое количество пирожных следует выпекать?
Решение задачи
Используем игровой подход. В рассматриваемой ситуации в качестве сознательного игрока А (статистика) выступает кафетерий «Мечта», принимающий решение об объемах выпуска кондитерских изделий. Его чистыми стратегиями будут: А1 – решение о выпуске 100 шт. кондитерских изделий в день; А2 – 120 шт.; А3 – 140 шт.; А4 – 160 шт. В качестве второго игрока будем рассматривать спрос на кондитерские изделия, под влиянием которого специалисты кафетерия принимают решение об объемах выпуска пирожных, – природу П. В данном случае природа может реализовать любое из четырех состояний: П1 – спрос на пирожные составляет 100 шт.; П2 – 120 шт.; П3 – 140 шт.; П4 – 160 шт. Итак, описанная ситуация формализуется в статистическую игру размерности 4х4 (таблица 7.5).
Таблица 7.5 – Платежная матрица
Вычислим выигрыши аij игрока А – значения совокупного показателя эффективности работы кафетерия при любом стечении обстоятельств (Аi; Пj) (i, j =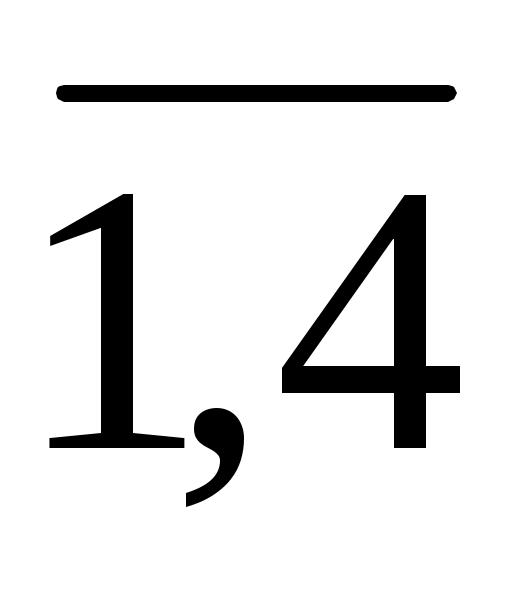
). Наиболее благоприятными будут комбинации (А1; П1), (А2; П2), (А3; П3) и (А4; П4), когда объем выпуска пирожных совпадает со спросом на них:
; 
;
; 
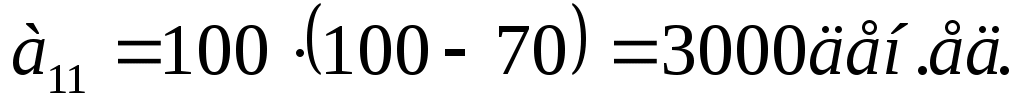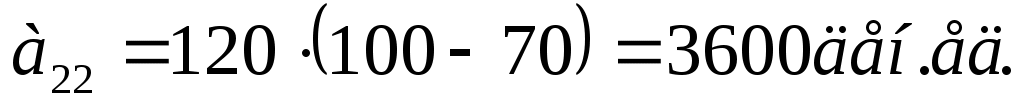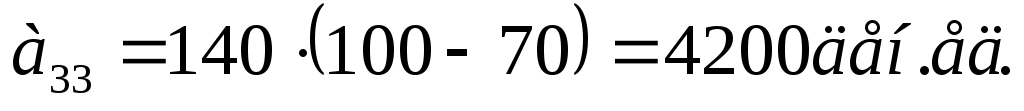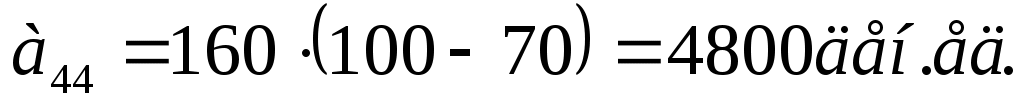
В ситуациях (А1; П2), (А1; П3), (А1; П4) кафетерий произведет 100 шт. пирожных при спросе на них соответственно в 120, 140, 160 шт. Поэтому кафетерий получит прибыль в размере 3000 ден. ед.
В ситуации (А2; П1), если кафетерий произведет 120 шт. пирожных при спросе на них в 100 шт., прибыль составит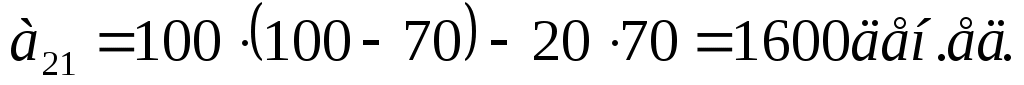
Аналогично вычисляются и остальные элементы платежной матрицы (таблица 7.5).
Как видно из таблицы 7.5, нижняя чистая цена игры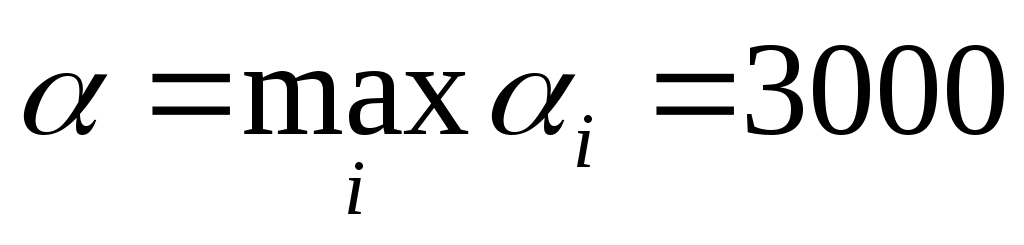
, а верхняя чистая цена 
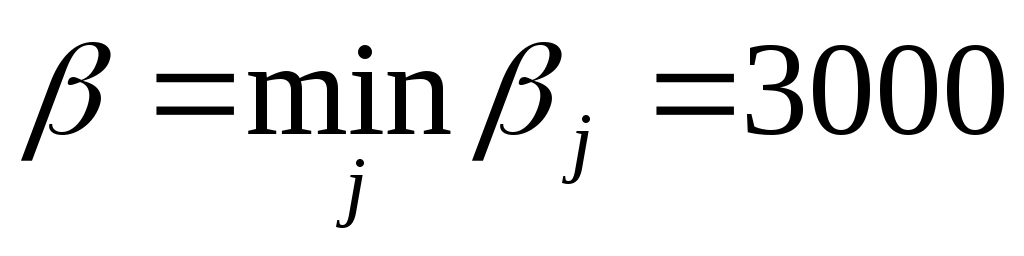, т.е. = - игра имеет седловую точку в чистых стратегиях и чистую цену игры ν = α = β. Оптимальными для игроков будут соответственно максиминная и минимаксная стратегии, т.е. для кафетерия оптимальной будет стратегия А1 (объем выпуска пирожных – 100 шт.).
В условии задачи известны вероятности состояний спроса, поэтому в качестве оптимальной по критерию Байеса принимается чистая стратегия Аi, при которой максимизируется средний выигрыш статистика. Тогда по формуле (7.9) находим значения средних выигрышей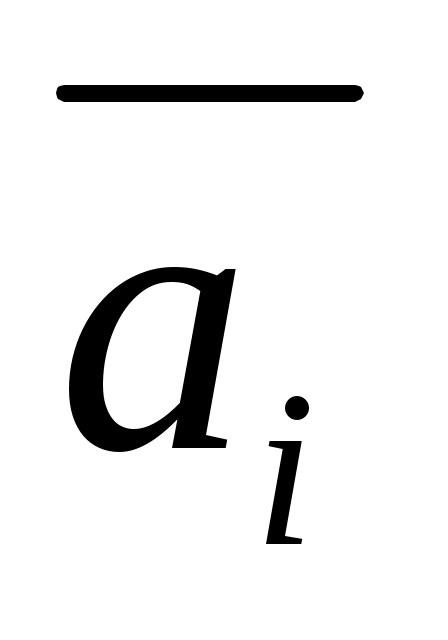
для каждой чистой стратегии (см. столбец 
таблицы 7.5) и устанавливаем по формуле (7.10), что наибольший средний выигрыш, равный 3000 ден. ед., достигается при стратегии
А1 (кафетерий должен выпускать 100 шт. пирожных в день), которая и будет оптимальной по критерию Байеса.
Задачи для самостоятельного решения
Задача 1
На каждой из двух торговых баз ассортиментный минимум составляет одинаковый набор товаров из четырех видов. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар, отличный от товара, завезенного в магазин В, то товар будет пользоваться спросом, и магазин А от его реализации получит прибыль с, денежных единиц. Если же в магазины А и В завезены товары одинакового вида, то товар в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по хранению и, возможно, порче товара в размере d, денежных единиц.
Требуется формализовать конфликтную ситуацию, построить матрицу игры и дать рекомендации по выбору оптимальной смешанной стратегии магазина А при числовых данных, представленных в таблице 7.6.
Таблица 7.6 – Исходные данные по вариантам
Задача 2
Предприятие может выпускать три вида продукции: А, Б и В. Объемы реализации продукции зависят от спроса, который может находиться в одном из состояний — C1, C2 и С3. Значения величины прибыли, которую получит предприятие при выпуске единицы i-го вида продукции при j-м состоянии спроса, заданы матрицей
Определить с помощью инструмента Поиск решения MS Excel оптимальные пропорции объемов выпуска продукции, гарантирующие максимальную среднюю величину прибыли при любом состоянии спроса. Вероятности наступления различных величин спроса неизвестны.
Задача 3
Небольшая частная фирма производит молочную продукцию. Один из ее продуктов — творожная масса. Необходимо решить, какое количество творожной массы следует производить в течение месяца, если вероятность того, что спрос составит 100, 150 или 200 кг равна соответственно 0,2; 0,5; 0,3. Затраты на производство 1 кг равны 1000 ден. ед. Фирма продает массу по цене 1200 ден. ед. за 1 кг. Если масса не продается в течение месяца, то она снимается с реализации и фирма не получает дохода.
Дать рекомендации, сколько творожной массы производить фирме.
Задача 4
Объем реализации товара Т за рассматриваемый период колеблется в зависимости от покупательского спроса в пределах от 4 до 6 ед. Прибыль торгового предприятия от единицы реализованного товара Т равна 2 ден. ед. Если запасенный товар полностью реализовать не удастся, то расходы на содержание и хранение остатка составят 3 ден. ед. за единицу товара.
Используя игровой подход, определить оптимальный уровень запаса товара Т, обеспечивающий торговому предприятию наивысшую эффективность работы.
Задача 5
Предприятие общественного питания занимается реализацией пирожных собственного производства. Объемы реализации пирожных зависят от спроса, который может находиться в одном из состояний – С1, С2, С3, С4. Значения величины прибыли, которую получит организация при реализации i-гo объема пирожных при j-м состоянии спроса, заданы в таблице 7.7.
Таблица 7.7 – Исходные данные для решения задачи
(7.8)Применяется две группы критериев — использующих и не использующих априорные вероятности qj состояний природы. К первой группе относятся критерии Байеса и Лапласа.
В качестве оптимальной по критерию Байеса принимается чистая стратегия Аi, при которой максимизируется средний выигрыш статистика
, (7.9)то есть обеспечивается
. (7.10)Если статистику представляются в равной мере правдоподобными все состояния Пj природы, то
и оптимальной по критерию Лапласа считается чистая стратегия Аi, обеспечивающая . (7.11)Ко второй группе критериев, применяемых при неизвестных априорных вероятностях состояний природы, относятся критерии Вальда, Сэвиджа и Гурвица.
Оптимальной по критерию Вальда считается чистая стратегия Аi, при которой наименьший выигрыш статистика будет максимальным, то есть ему обеспечивается
.Для смешанных стратегий критерий Вальда формулируется так: оптимальной считается та смешанная стратегия, при которой минимальный средний выигрыш статистика
будет максимальным, то есть стратегия р*, найденная из условия .Оптимальной по критерию Сэвиджа считается та чистая стратегия Аi, при которой минимизируется величина ri максимального риска, то есть обеспечивается
.
Для смешанных стратегий критерий Сэвиджа формулируется так: оптимальной считается та смешанная стратегия, при которой максимальный средний риск статистика
минимизируется, то есть стратегия р*, найденная из условия .Оптимальной по критерию Гурвица считается чистая стратегия Аi, найденная из условия
где принадлежит интервалу (0; 1) и выбирается из субъективных соображений. При = 1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда, а при = 0 — в критерий крайнего оптимизма.Пример решения задачи
Постановка задачи. Кафетерий «Мечта» реализует кондитерские изделия собственного изготовления. Спрос на пирожные может составить 100, 120, 140 или 160 шт. с вероятностью 0,2; 0,3; 0,4; 0,1 соответственно. Затраты на производство одного пирожного составляют 70 ден. ед., а цена реализации — 100 ден. ед. Если пирожные не продаются в течение 36 ч, они портятся и магазин несет убытки.
Какое количество пирожных следует выпекать?
Решение задачи
Используем игровой подход. В рассматриваемой ситуации в качестве сознательного игрока А (статистика) выступает кафетерий «Мечта», принимающий решение об объемах выпуска кондитерских изделий. Его чистыми стратегиями будут: А1 – решение о выпуске 100 шт. кондитерских изделий в день; А2 – 120 шт.; А3 – 140 шт.; А4 – 160 шт. В качестве второго игрока будем рассматривать спрос на кондитерские изделия, под влиянием которого специалисты кафетерия принимают решение об объемах выпуска пирожных, – природу П. В данном случае природа может реализовать любое из четырех состояний: П1 – спрос на пирожные составляет 100 шт.; П2 – 120 шт.; П3 – 140 шт.; П4 – 160 шт. Итак, описанная ситуация формализуется в статистическую игру размерности 4х4 (таблица 7.5).
Таблица 7.5 – Платежная матрица
-
П1(100)
П2(120)
П3(140)
П4(160)
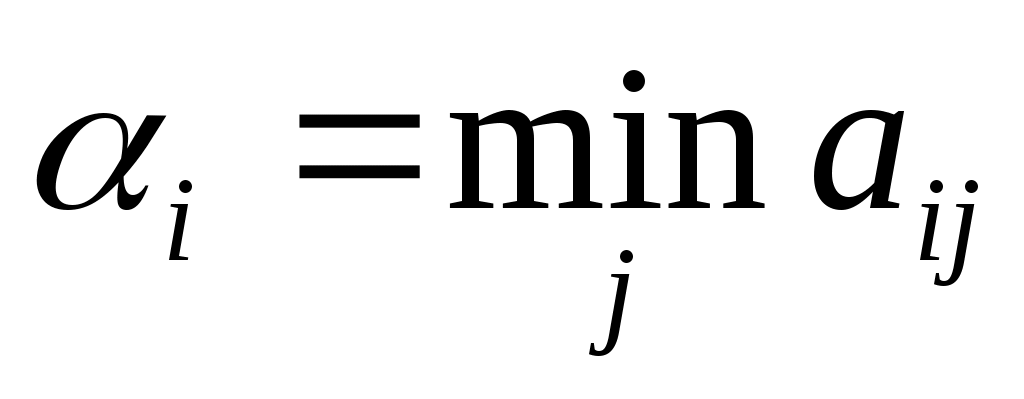
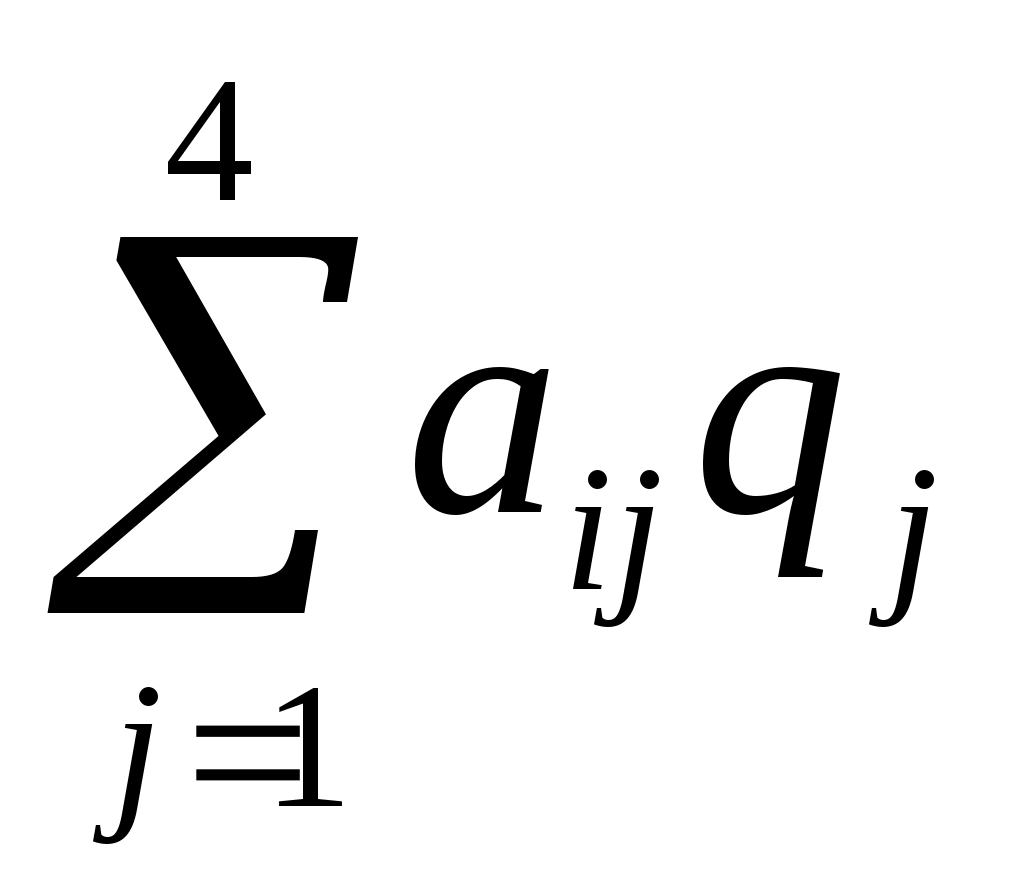
А1(100)
3000
3000
3000
3000
3000
3000
А2(120)
1600
3600
3600
3600
1600
3200
А3(140)
200
2200
4200
4200
200
2800
А4(160)
-1200
800
2800
4800
-1200
1600
3000
3600
4200
4800
qj
0,2
0,3
0,4
0,1
Вычислим выигрыши аij игрока А – значения совокупного показателя эффективности работы кафетерия при любом стечении обстоятельств (Аi; Пj) (i, j =
). Наиболее благоприятными будут комбинации (А1; П1), (А2; П2), (А3; П3) и (А4; П4), когда объем выпуска пирожных совпадает со спросом на них: ; ; ; В ситуациях (А1; П2), (А1; П3), (А1; П4) кафетерий произведет 100 шт. пирожных при спросе на них соответственно в 120, 140, 160 шт. Поэтому кафетерий получит прибыль в размере 3000 ден. ед.
В ситуации (А2; П1), если кафетерий произведет 120 шт. пирожных при спросе на них в 100 шт., прибыль составит
Аналогично вычисляются и остальные элементы платежной матрицы (таблица 7.5).Как видно из таблицы 7.5, нижняя чистая цена игры
, а верхняя чистая цена , т.е. = - игра имеет седловую точку в чистых стратегиях и чистую цену игры ν = α = β. Оптимальными для игроков будут соответственно максиминная и минимаксная стратегии, т.е. для кафетерия оптимальной будет стратегия А1 (объем выпуска пирожных – 100 шт.).В условии задачи известны вероятности состояний спроса, поэтому в качестве оптимальной по критерию Байеса принимается чистая стратегия Аi, при которой максимизируется средний выигрыш статистика. Тогда по формуле (7.9) находим значения средних выигрышей
для каждой чистой стратегии (см. столбец таблицы 7.5) и устанавливаем по формуле (7.10), что наибольший средний выигрыш, равный 3000 ден. ед., достигается при стратегии
А1 (кафетерий должен выпускать 100 шт. пирожных в день), которая и будет оптимальной по критерию Байеса.
Задачи для самостоятельного решения
Задача 1
На каждой из двух торговых баз ассортиментный минимум составляет одинаковый набор товаров из четырех видов. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар, отличный от товара, завезенного в магазин В, то товар будет пользоваться спросом, и магазин А от его реализации получит прибыль с, денежных единиц. Если же в магазины А и В завезены товары одинакового вида, то товар в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по хранению и, возможно, порче товара в размере d, денежных единиц.
Требуется формализовать конфликтную ситуацию, построить матрицу игры и дать рекомендации по выбору оптимальной смешанной стратегии магазина А при числовых данных, представленных в таблице 7.6.
Таблица 7.6 – Исходные данные по вариантам
-
Вариант
1
2
3
4
5
6
7
8
9
10
с1
10
137
121
43
68
62
41
52
325
220
с2
16
223
79
78,3
75
57
45
63
451
324
с3
23
87
68
53
56
43
38
21
123
156
с4
7
13
37
48
89
65
44
132
321
235
d1
8
125
98
38,5
66
23
22
41
112
120
d2
12
201
67
72
72
32
36
46
320
410
d3
24
79
57
49
53
31
30
23
110
210
d4
5
12
43
43
77
34
30
83
220
330
Задача 2
Предприятие может выпускать три вида продукции: А, Б и В. Объемы реализации продукции зависят от спроса, который может находиться в одном из состояний — C1, C2 и С3. Значения величины прибыли, которую получит предприятие при выпуске единицы i-го вида продукции при j-м состоянии спроса, заданы матрицей
Определить с помощью инструмента Поиск решения MS Excel оптимальные пропорции объемов выпуска продукции, гарантирующие максимальную среднюю величину прибыли при любом состоянии спроса. Вероятности наступления различных величин спроса неизвестны.
Задача 3
Небольшая частная фирма производит молочную продукцию. Один из ее продуктов — творожная масса. Необходимо решить, какое количество творожной массы следует производить в течение месяца, если вероятность того, что спрос составит 100, 150 или 200 кг равна соответственно 0,2; 0,5; 0,3. Затраты на производство 1 кг равны 1000 ден. ед. Фирма продает массу по цене 1200 ден. ед. за 1 кг. Если масса не продается в течение месяца, то она снимается с реализации и фирма не получает дохода.
Дать рекомендации, сколько творожной массы производить фирме.
Задача 4
Объем реализации товара Т за рассматриваемый период колеблется в зависимости от покупательского спроса в пределах от 4 до 6 ед. Прибыль торгового предприятия от единицы реализованного товара Т равна 2 ден. ед. Если запасенный товар полностью реализовать не удастся, то расходы на содержание и хранение остатка составят 3 ден. ед. за единицу товара.
Используя игровой подход, определить оптимальный уровень запаса товара Т, обеспечивающий торговому предприятию наивысшую эффективность работы.
Задача 5
Предприятие общественного питания занимается реализацией пирожных собственного производства. Объемы реализации пирожных зависят от спроса, который может находиться в одном из состояний – С1, С2, С3, С4. Значения величины прибыли, которую получит организация при реализации i-гo объема пирожных при j-м состоянии спроса, заданы в таблице 7.7.
Таблица 7.7 – Исходные данные для решения задачи
-
Объемы реализации
Состояния спроса
C1
C2
C3
C4
V1
6
12
20
24
V2
9
7
9
28
V3
23
18
15
19
V4
27
24
21
15