Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Обозначим через р₁, ..., р_m вероятности, с которыми игрок А использует в ходе игры свои чистые стратегии A₁, ..., А_m. Для вероятностей р_i выполняются условия:
. (7.3)

Упорядоченное множество , элементы кото­рого удовлетворяют условиям (7.3), полностью определяет ха­рактер игры игрока А и называется его смешанной стратеги­ей.

Аналогично упорядоченное множество , эле­менты которого удовлетворяют соотношениям

, (7.4)
является смешанной стратегией игрока В.

Итак, пусть игроки А и В применяют смешанные стратегии р и q. Это означает, что игрок А использует стратегию A_i с вероятностью p_i, а игрок В – стратегию В_j с вероятностью q_j. При использовании смешанных стратегий игра приобрета­ет случайный характер, случайной становится и величина вы­игрыша игрока А (проигрыша игрока В). В связи с этим мож­но вести речь лишь о средней величине (математическом ожи­дании) выигрыша (проигрыша). Эта величина явля­ется функцией от смешанных стратегий р и q и определяется по формуле

. (7.5)
Функция (7.5) называется платежной функцией игры с матрицей.

Нижней ценой игры будем называть число α, определяемое по формуле , a верхней ценой игры – число β, определяемое по формуле

. (7.6)
Оптимальными являются смешанные стратегии р* и q* игроков А и В, удовлетворяющие равенству
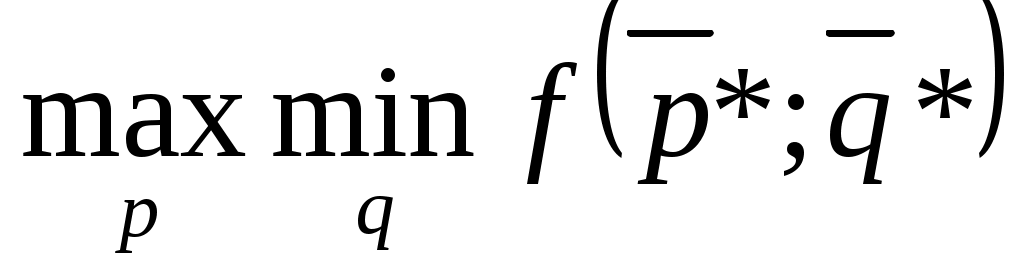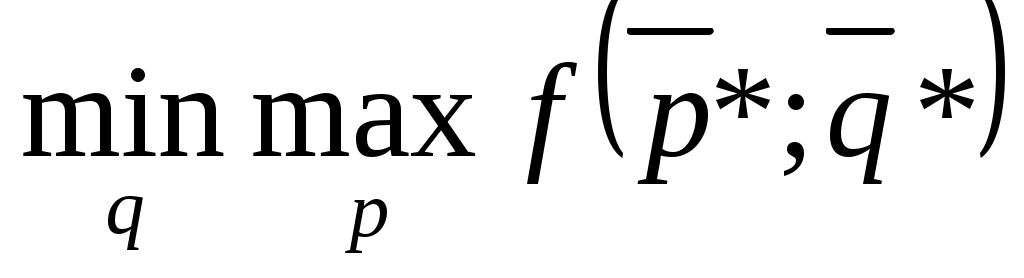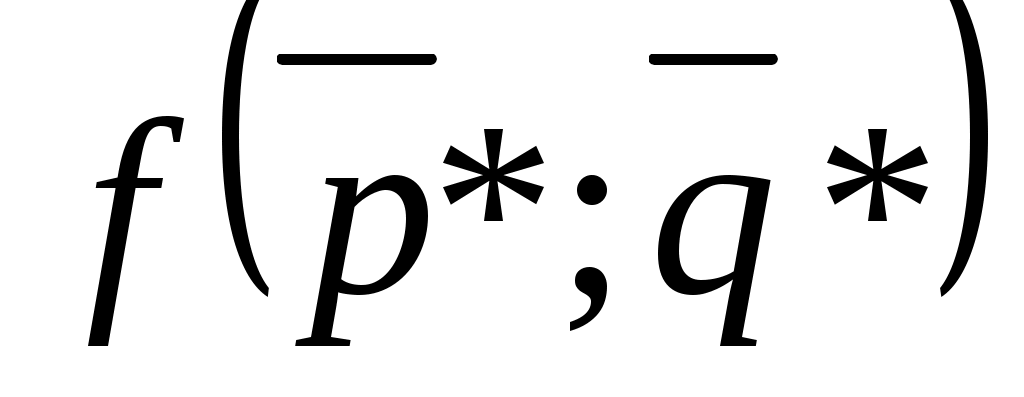= = . (7.7)
Величину 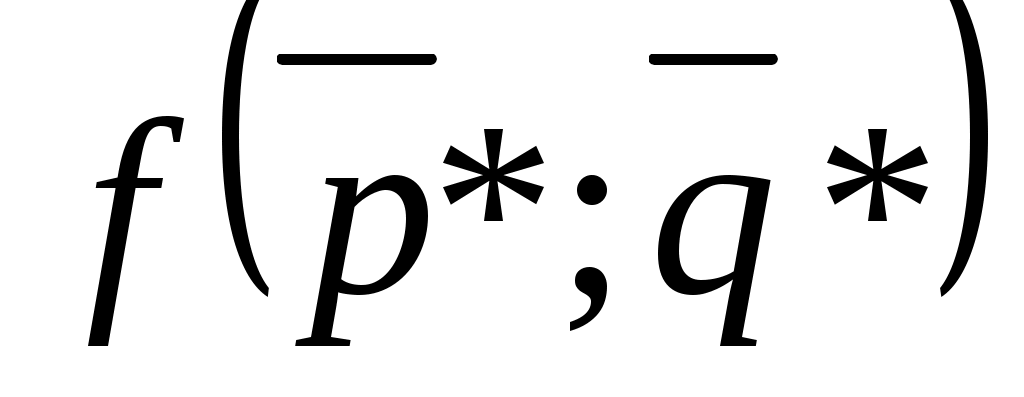, полученную по формуле (7.7), называют

---

ценой игры v.
Пример решения задачи
Постановка задачи. На каждой из двух торговых баз ассортиментный ми­нимум составляет одинаковый набор товаров из четырех видов. Магазины, обо­значим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в ма­газин В, более высокого качества. Если магазин А завезет с базы товар, отлич­ный от товара, завезенного в магазин В, то товар будет пользоваться спросом, и магазин А от его реализации получит прибыль с, денежных единиц. Если же в магазины А и В завезены товары одинакового вида, то товар в магазине А спро­сом пользоваться не будет, поскольку такой же товар, по такой же цене, но бо­лее высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по хранению и, возможно, порче товара в размере d, денежных единиц.

Требуется формализовать конфликтную ситуацию, построить матрицу иг­ры и дать рекомендации по выбору оптимальной смешанной стратегии магази­на А при следующих числовых данных:

с1	с2	с3	с4	d1	d2	d3	d4
17	11	23	5	13	12	20	7

Решение задачи
1 Представим данную ситуацию в виде матричной игры. У руководства ма­газина А четыре стратегии: А_i - продавать товар i-го вида (i = 1,4). Аналогично у руководства магазина В стратегии В_j - продавать товар j-го вида (j = 1,4).

Построим платежную матрицу данной игры на рабочем листе MS Excel в ячейках А1:Е5 (таблица 7.1).
Таблица 7.1 – Платежная матрица

	А	В	С	D	E
1		В1	В2	В3	В4
2	А1	-13	17	17	17
3	А2	11	-12	11	11
4	А3	23	23	-20	23
5	А4	5	5	5	-7

---

Определим, имеет ли игра оптимальное решение в чистых стратегиях, т.е. проверим наличие седловой точки. Чтобы рассчитать верхнюю и нижнюю чис­тые цены игры, в столбец а_i (F1:F5) вводим функцию МИН, а в строку β_j (A6:E6) - функцию МАКС, получаем матрицу следующего вида (таблица 7.2).
Таблица 7.2 – Определение седловой точки

	А	В	С	D	E	F
1		В1	В2	В3	В4	ai
2	А1	-13	17	17	17	-13
3	А2	11	-12	11	11	-12
4	А3	23	23	-20	23	-20
5	А4	5	5	5	-7	-7
6	βj	23	23	17	23

Далее аналогично вычисляем:

; .

Так как а β, то игра не имеет решения в чистых стратегиях.
2 Решение игры в смешанных стратегиях
2.1 Преобразование платежной матрицы. Чтобы свести игру к задаче ли­нейного программирования, увеличим все элементы платежной матрицы на 20 (таблица 7.3).

Таблица 7.3 – Преобразование платежной матрицы

	А	В	С	D	E
1		В1	В2	В3	В4
2	А1	7	37	37	37
3	А2	31	8	31	31
4	А3	43	43	0	43
5	А4	25	25	25	13

---

2.2 Построение математической модели.

Задача линейного программирования для игрока А:


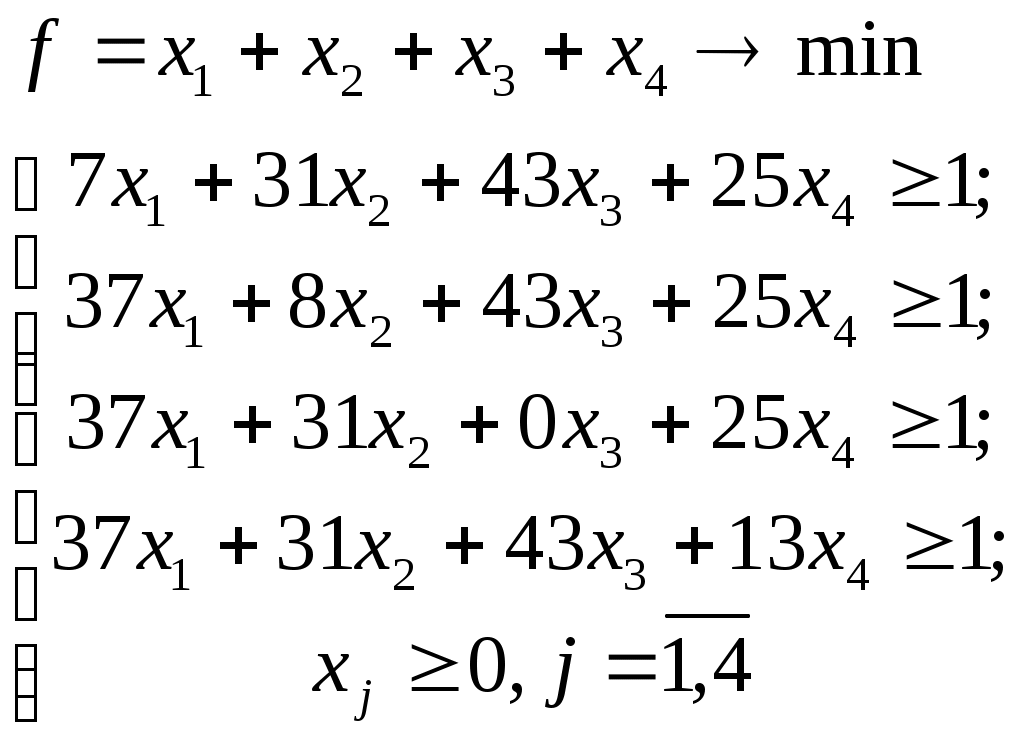
где , p_j – вероятность, с которой игрок А применяет свою j-ю чистую стратегию, v - цена игры.
2.3. Технология решения задачи средствами Excel. Строим следующую таблицу (таблица 7.4).
Таблица 7.4 – Решение задачи в Excel

	А	В	С	D	E	F	G	H
1	Имя	Переменные
2		Х1	Х2	Х3	Х4
3	Значение	0,0129	0,0168	0,009	0
4	Нижняя граница
5	Верхняя граница
6						ЦФ	Направление ЦФ
7	Коэффициент ЦФ	1	1	1	1	0,039	min
8		Ограничения
9	Вид					левая часть	знак	правая часть
10	1	7	31	43	25	1	>	1
11	2	37	8	43	25	1	>	1
12	3	37	31	0	25	1	>	1
13	4	37	31	43	13	1,387	>	1

---

Решив данную задачу средствами Excel, получаем:
х₁ = 0,0129; х₂ = 0,0168; х₃ = 0,009; f_min = 0,039.
Для определения смешанной стратегии, воспользуемся формулами:
.
Отсюда смешанная стратегия: р = (0,333; 0,434; 0,233; 0), N =25,79.
3 Анализ полученных результатов

Итак, оптимальной стратегией магазина А будет продажа товаров в сле­дующей пропорции: 33,3 % товара 1-го вида; 43,4 % товара 2-го вида; 23,3 % товара 3-го вида. Средняя прибыль составит 25,79 ден. ед.
2 Решение статистических игр по различным критериям
Нередко при решении экономических задач возникает необходимость выбора оптимального решения в условиях не­определенности и риска. Такие ситуации назы­ваются играми с природой (иногда статистическими игра­ми). Термин «природа» характеризует некоторую объективную действительность, которая выступает как не имеющий конкретной цели и случайным образом выбираю­щий очередные ходы партнер по игре. Природа безразлична к выигрышу.

Сторона, принимающая решение (игрок А или статис­тик), имеет т стратегий: А₁, А₂, ..., А_m. Природа может реализовать п возможных состояний: П₁, П₂,..., П_n. Поскольку при­рода не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить с помощью вы­игрышей a_ij игрока А для каждой пары стратегий А_i и П_j. Все показатели игры записываются в виде платежной матрицы:

.

Часто построение платежной матрицы является наиболее трудоемким этапом подготовки принятия решения. При анализе игры с природой вводится также показа­тель, позволяющий оценить, насколько то или иное состоя­ние природы влияет на исход ситуации. Этот показатель на­зывается риском.

Риском r_ij статистика, когда он пользуется чистой стра­тегией А_i при состоянии П_j природы, называется разность между максимальным выигрышем , который он мог бы получить, достоверно зная, что природой будет реализо­вано именно состояние П_j, и тем выигрышем

---