Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Общее условие, которое отвечает данной теории, имеет вид

(4.32)

где _max – расчетная величина наибольшего касательного напряжения

для исследуемого напряженного состояния;

₀ - предельное значение касательного напряжения, определяемого из опыта на простое растяжение.

В случае объёмного напряженного состояния при ₁₂₃ наиболь-

шее касательное напряжение определяется по формуле:

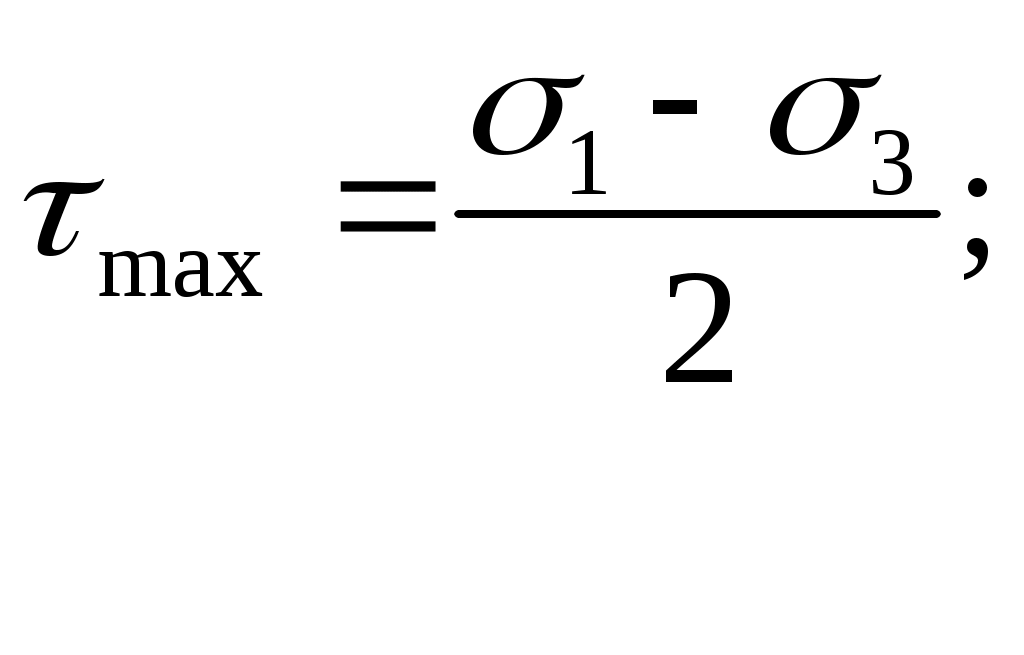(4.33)

напряжение ₀ находится из равенства



Тогда, условие () можно записать так:



Расчетную формулу запишем в виде

(4.34)

Для плоского напряженного состояния запишется в виде



На практике нередко встречаются случаи, когда _у=0. Положив тогда _у= и _ху=, получим

(4.35)

Основной недостаток третьей теории состоит в том, что в случае объёмного напряженного состояния ею не учитывается влияние главного напряжения ₂.

Эта теория лучше всего подтверждается опытами с пластическими материалами, одинаково сопротивляющимися как растяжению, так и сжатию.
Определим предел текучести при чистом сдвиге

,

Отсюда

(4.36)
4.6.5. Четвертая теория прочности (энергетическая теория формоизменения)

Критерием прочности принимается количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Согласно этой теории опасное состояние (текучесть) в случае объёмного напряженного состояния при ₁₂

---

₃ наступает тогда, когда удельная энергия формоизменения достигнет своего предельного значения. Последнее определяется из опыта на простое растяжение в момент текучести.

Условие наступления текучести



Условие прочности



Потенциальная энергия формоизменения при объёмном напряженном состоянии равна



Приведем к виду



При простом растяжении в момент текучести (₁=_Т, ₂=₃=0) имеем



Следовательно, условие прочности можно записать так

(4.37)

Эта теория лучше всего подтверждается опытами с пластическими материалами, одинаково сопротивляющимися как растяжению, так и сжатию.

Наступление текучести отображается энергетической теорией лучше, чем теорией наибольших касательных напряжений.

Для частного случая при _у=0, положив _z= и _zу=, имеем

(4.38)

Определим предел текучести при чистом сдвиге

,

Отсюда

(4.39)


4.6.6. Теория прочности Мора

Теория прочности Мора позволяет учесть различное сопротивление материалов растяжению и сжатию. Мор исходил из предположения, что прочность материалов при объёмном напряженном состоянии зависит, главным образом, от величины и знака главных напряжений ₁ и₃, что подтвердил опытами на различных материалах. Учитывая это, меняя предельное напряженное состояние, строится семейство предельных кругов Мора, проводят огибающую для этих кругов, которую называют предельной огибающей. При наличии предельной огибающей расчет на прочность прост: по найденным главным напряжениям

---

₁ и₃ строят круг. Прочность будет обеспечена, если он целиком лежит внутри огибающей. На практике действительную огибающую заменяют прямыми, касательными в точках К₁ и К₂ лишь к двум главным кругам, которые строят по данным опыта на растяжение и сжатие (рис. ). Эти прямые являются границами области прочности состояний. Вместе с тем они устанавливают линейную зависимость между напряжениями ₁ и₃ всякого напряженного состояния, главный круг которого касается этих прямых:



Соответствующая формула запишется так:

(4.40)

г
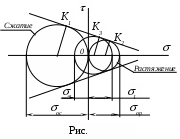
де через k обозначено отношение предела текучести при растяжении к пределу текучести при сжатии:

()

Для хрупких материалов отношение заменяется отношением

В частном случае, если материал имеет при растяжении и сжатии одинаковые пределы текучести, k=1. Тогда формула () переходит в полученную ранее формулу (4.34).

Наилучшие результаты выведенная расчетная формула дает для смешанных напряженных состояний, Т.Е. при ₁>0 и ₃ <0 .
Вопросы для самопроверки

1. 
   Какие имеются виды напряженного состояния материала?
   
2. 
   Каковы напряжения в наклонных сечения бруса при плоском напряженном состоянии?
   
3. 
   Как определяются главные напряжения?
   
4. 
   Как определяются экстремальные касательные напряжения?
   
5. 
   Каковы нормальные напряжения на площадках с_max?
   
6. 
   Как получить формулу круга Мора?
   
7. 
   Как определяются главные относительные деформации?
   
8. 
   Как определяется удлинение в произвольном направлении?
   
   0. 
      9. Чему равна относительная объёмная деформация ?
      

---

10.Чему равна потенциальная энергия при объёмном напряженном

состоянии?

11. Как получить формулу обобщенного закона Гука для линейно

упругого тела?

12. Сколько основных теорий прочности?

13. В чем заключается идея каждой теории прочности?

14. Какое напряженное состояние называется эквивалентным?

!5. Какими теориями и в каких случаях следует пользоваться в расчетах на прочность?

5. Чистый сдвиг

5.1. Понятие о чистом сдвиге

В некоторых случаях прочность, а также жёсткость элементов конструкции связаны с сопротивлением материала сдвигу. Для более тщательного изучения этой деформации было введено понятие чистого сдвига.

Чистым сдвигом называют такой вид плоского напряженного и деформированного состояния, при котором на двух взаимно перпендикулярных площадках, ориентированных определённым образом, действуют только касательные напряжения.


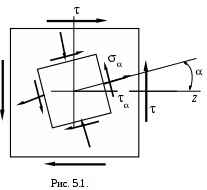
Указанные площадки называют площадками чистого сдвига (см. рис. 5.1.) .

Принимая эти площадки за исходные и полагая _z=_y=0, _zy=, получим:

_=-sin2 (5.1)

_cos2(5.2)
Формула (5.1) указывает, что _обращается в нуль только на площадках чистого сдвига (при  или ) На всех других площадках нормальные напряжения не равны нулю, что и показано на рисунке. На любых других взаимно перпендикулярных площадках они равны по величине и противоположны по знаку т.е. _+900=-_. Таким образом, при чистом сдвиге наблюдается «закон парности нормальных напряжений», отсюда следует, что при чистом сдвиге главные напряжения удовлетворяют условию ₁=-₂.
Типичным примером тела, во всех точках которого имеет место чистый сдвиг, является скручиваемая тонкостенная труба.
5.2. Анализ напряженного состояния при чистом сдвиге

Найдём величину экстремальных напряжений при чистом сдвиге с помощью формул (5.1) и (5.2). Первая из них указывает, что при  (sin2) имеем экстремальные нормальные напряжения: ₁ и ₃- .

Экстремальные касательные напряжения определим по формуле (5.2): при _тах.
И

---

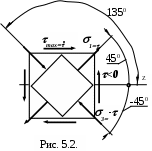
так, при чистом сдвиге главные напряжения – сжимающие и растягивающие – равны между собой и числено равны экстремальным касательным напряжениям. Главные площадки составляют с площадками чистого сдвига угол 45⁰.

(см. рис. 5.2.)
Построим круг напряжений (см. рис. 5.3.)

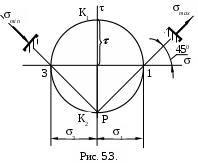Круг напряжений, изображающий точки исходных площадок

К₁(0,-) и К₂(0,), которые лежат на оси , и центр круга – в начале координат.

Полюс Р(0,-) совпадает с точкой К₁(0,-). Естественно, что получаются те же самые результаты.

Чистый сдвиг единственный вид плоского напряженного состояния, при котором отсутствует изменение объёма материала, т.к.

относительная объёмная деформация в этом случае, когда (₁=-₃=, ₂=0):
V/V₀(1/E)(1-2v)(_x+_y+_z) (1/E)(1-2v)(₁+₂+₃)=0. (5.3)


5.3. Закон Гука при чистом сдвиге
Рассмотрим деформацию элемента, ограниченного площадками сдвига.

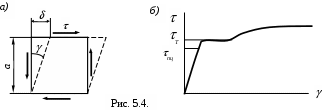
Величину  (см. 5.4,а) называют абсолютным сдвигом, а отношение  а - относительным сдвигом, или углом сдвига. Экспериментально установлено (см. 5.4,б), что в определённых пределах деформация сдвига происходит упруго, а величина её пропорциональна касательным напряжениям 

G, или G (5.4)

Это соотношение называют законом Гука при сдвиге.




Коэффициент пропорциональности G между касательным напряжением и углом сдвига называют модулем упругости при сдвиге, или модулем упругости второго рода. Модуль G имеет размерность напряжений [Па], так как  - величина безразмерная.

Модулем упругости при сдвиге G связан с модулем Е соотношением

G=0.5Е/(1+v). (5.5)

Эта формула показывает, что три постоянные G, Е и v, характеризующие упругие свойства изотропного материала, связаны между собой.
Вид диаграммы -,получаемый также из опыта, напоминает аналогичную диаграмму при растяжении.

Напряжение _пц – предел пропорциональности при сдвиге –

---