Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 390
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
является границей справедливости закона Гука.
Напряжение Т - предел текучести при сдвиге, который сменяется стадией упрочнения (некоторым повышением напряжений с ростом сдвигов). Для многих материалов величина Тсвязана с пределом текучести при растяжении Т соотношением
_
ТТ
5.4. Потенциальная энергия при чистом сдвиге
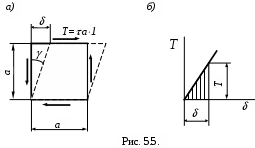
При деформации элемента, показанного на рис. 5.5,а), работу совершает только касательная сила Т, приложенная к верхней грани на перемещении . Сдвиг в пределах закона Гука пропорционален силе Т, что показано на рис. 5.5,б). Работа этой силы А численно равна потенциальной энергии сдвига U, определяется выражением
A=U=0.5 T,
или, учитывая, что Т= а, а = а, получим
U=0.5а2 (5.6)
Удельная потенциальная энергия деформации сдвига равна
u=U/Vоб=(0.5а2)/a20.5=(0.52)/G. (5.7)
Вопросы для самопроверки
6. Кручение
Кручением называют такой случай деформации стержня, при котором в его поперечных сечениях возникают только одни крутящие моменты; нормальная сила, изгибающие моменты и поперечные силы равны нулю.
Исследования показали, что характер деформации скручиваемого стержня в значительной степени зависит от формы его поперечного сечения. Среди стержней с различными формами поперечного сечений, подвергаемых кручению, особое место занимают стержни с круглым или кольцевым сечением, имеющие наибольшее распространение в технике.
Круглые стержни, работающие на кручение, механики называют валами.
Ранее мы уже познакомились, c методом сечений (РОЗУ ), с вычислением крутящих моментов (МК=МZ=Т) и построением их эпюр. Для бруса постоянного сечения наиболее опасным является сечение, в котором крутящий момент имеет наибольшее абсолютное значение.
6.1. Напряжения и деформации при кручении стержня с круглым поперечным сечением
Статическая сторона задачи.
Зная величину крутящего момента в том или ином сечении, представим его статическим уравнением
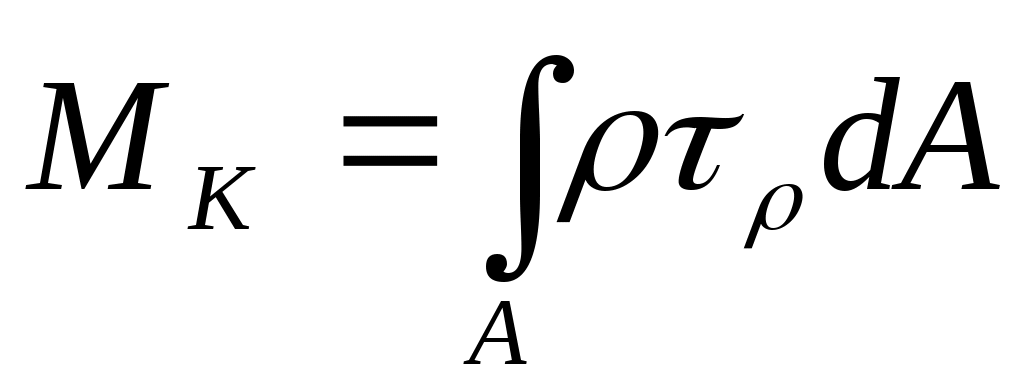 , (6.1)
, (6.1)
где - касательное напряжение, действующее на элементарной площадке dA, расположенной от центра сечения на расстоянии произвольного радиуса .
Пока это уравнение решить нельзя т.к. неизвестен закон распределения напряжении по сечению. Рассмотрим стержень радиуса r, заделанного одним концом, на свободном конце которого приложим пару сил с моментом М.
Геометрическая сторона задачи.
Нанесем на боковую поверхность скручиваемого стержня ортогональную сетку (см.рис. 6.1,а). Оказывается, что после закручивания прямоугольники, образованные сеткой, перекашиваются, ось стержня остаётся прямолинейной, контуры поперечных сечений (круглые и плоские до деформации) остаются такими же и после деформации. При кручении происходит поворот одного сечения относительно другого на некоторый угол , называемый углом закручивания. Расстояние между поперечными сечениями практически не меняются, а это значит, что продольные волокна не удлиняются и не укорачиваются.
Описанные наблюдения характеризуют деформации волокон, лежащих на поверхности стержня, но не позволяют делать какие-либо заключения о деформации внутренних волокон. Для того чтобы сделать задачу вполне определённой, сформулируем гипотезы, которые положим в основу дальнейших выводов.
Будем предполагать, что:
1) сечения плоские до закручивания, остаются плоскими и после закручивания;
На основании принятых гипотез кручение круглого стержня можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения.
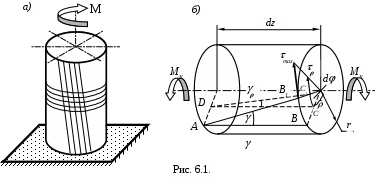
Рассмотрим (см. рис. 6.1,б) элемент стержня радиусом r, длиной dz с крутящим моментом МK.
Образующая АВ отклонится на малый угол и перейдет в положение АВ1. Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством
ВВ1 АВ
rddz.
Для произвольного волокна, отстоящего от центра стержня на расстоянии будет иметь
СС1 DC(ddz).
Физическая сторона задачи.
На основании закона Гука при сдвиге для двух указанных точек можно записать:
G=G(d dz)r; (6.2)
G=G(d dz). (6.3)
Сопоставляя формулы (6.2) и (6.3), замечаем, что касательные напряжения в точках поперечного сечения изменяются пропорционально расстоянию этих точек от оси стержня. Наибольшие напряжения наблюдаются в точках, наиболее удалённых от центра стержня. Представим графически закон распределения касательных напряжении для стержней круглого на рис. 6.2,а) и кольцевого сечения на рис. 6.2,б). По закону парности касательных напряжений касательные напряжения в каждой точке перпендикулярны радиусу и действуют не только в поперечных сечения стержня, но и в продольных.
В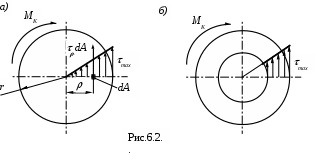
ыделим вокруг произвольной точки площадку dA, на которой будет действовать элементарная касательная сила dA. Момент этой силы относительно оси стержня равен
dMKdA.
Суммируя элементарные моменты, найдём полный крутящий момент:
т.е. получим формулу (6.1).
Подставляя в (6.1) вместо его значение из (6.3), получим
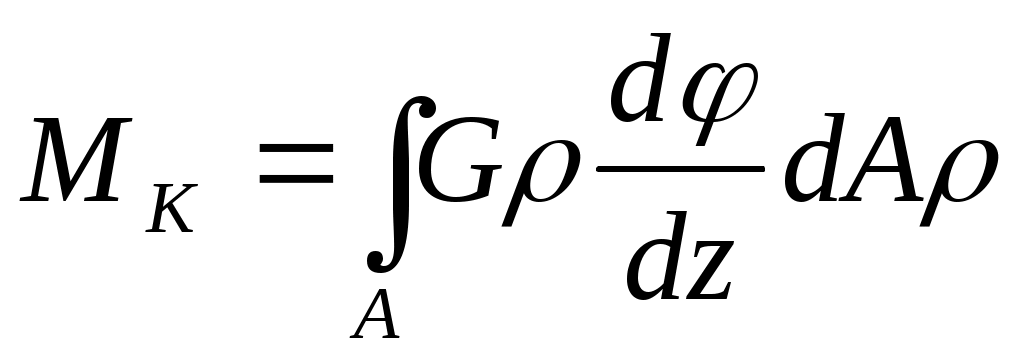 .
.
Вынесем за знак интеграла величину G(ddz), т.к. для всех точек поперечного сечения она одинакова, а также заметим, что 2dA=I представляет собой полярный момент инерции сечения. Тогда
МК=GI(ddz),
или (МК /GI)=(ddz), Подставляя полученное в (6.3) найденное выражение (ddz), и тогда окончательно получим
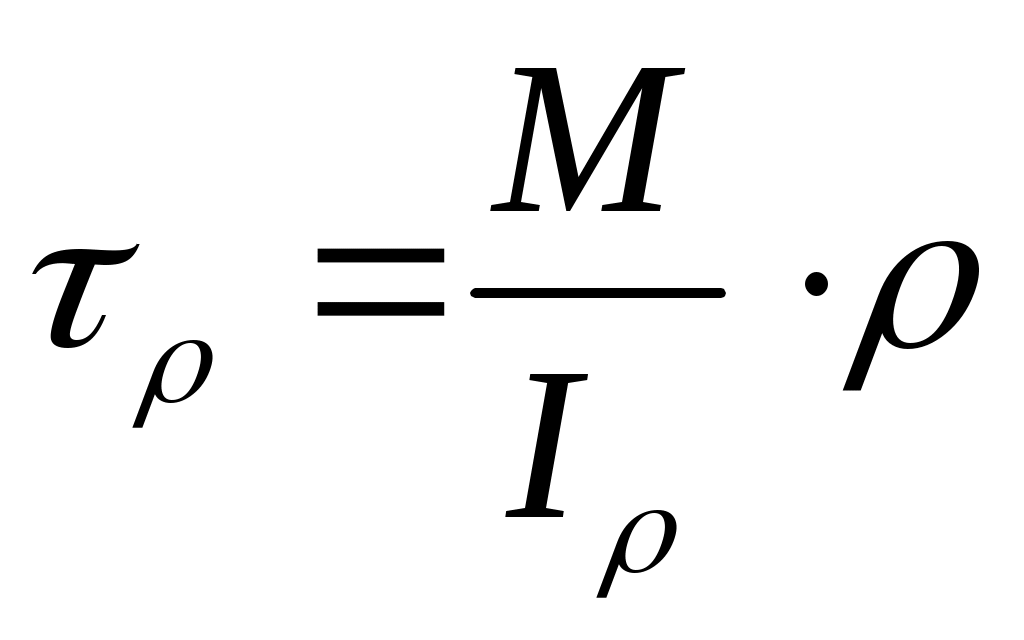 (6.4)
(6.4)
Эта формула позволяет определить в любой точке круглого поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле
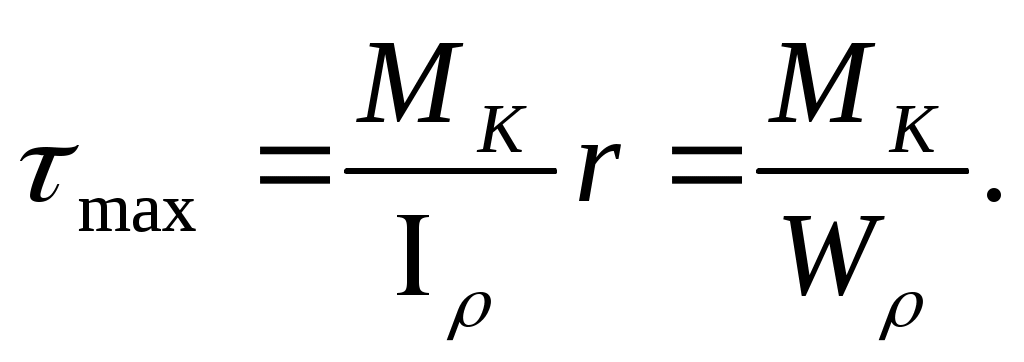
Величину W=(r) называют полярным моментом сопротивления
Полярный момент инерции для сплошного круглого сечения
r4d4
для кольцевого сечения с внешним диаметром D и внутренним d
(D4 ) (1-4)
где d / D.
Следовательно, моменты сопротивления имеют следующие значения:
для сплошного сечения Wr3d3 16
для кольцевого сечения W (D3 16) (1-4 ).
При определении угла закручивания () воспользуемся уравнением (а), из которого находим
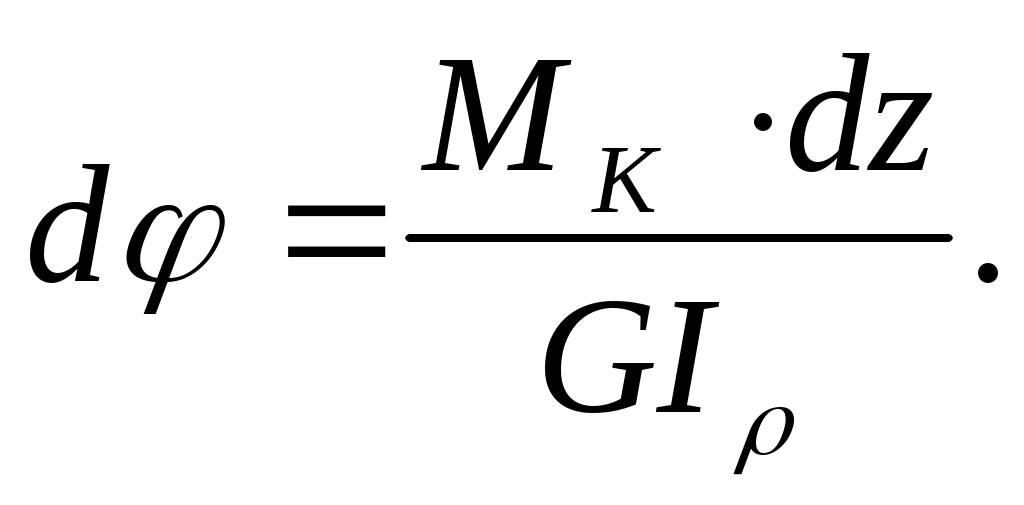
После интегрирования получим полный угол закручивания стержня на участке
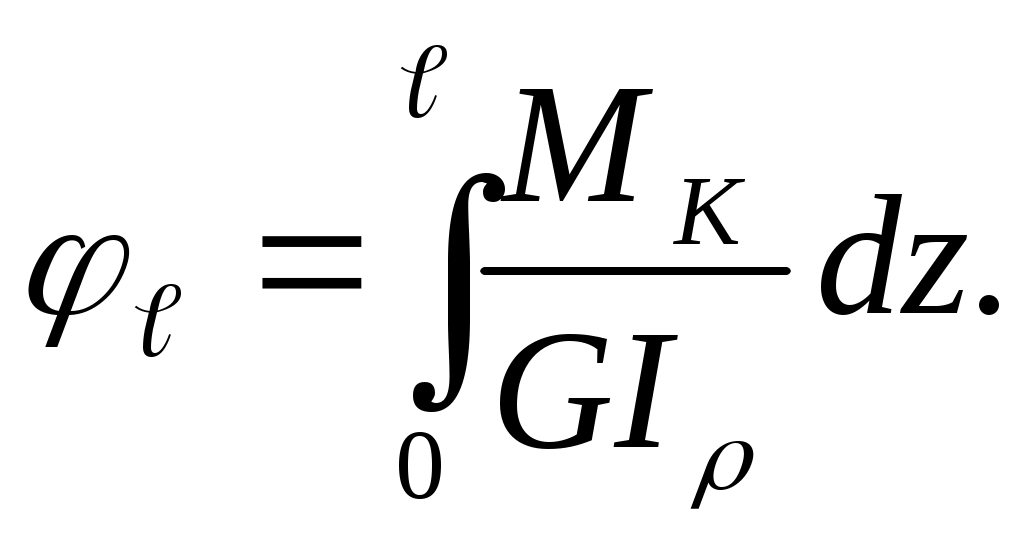 (6.5)
(6.5)
Величину GI называют жёсткостью стержня при кручении. Она характеризует сопротивление стержня закручиванию.
Если по всей длине стержня момент не меняется и стержень имеет постоянный диаметр, интегрируя выражение (6.5), получим
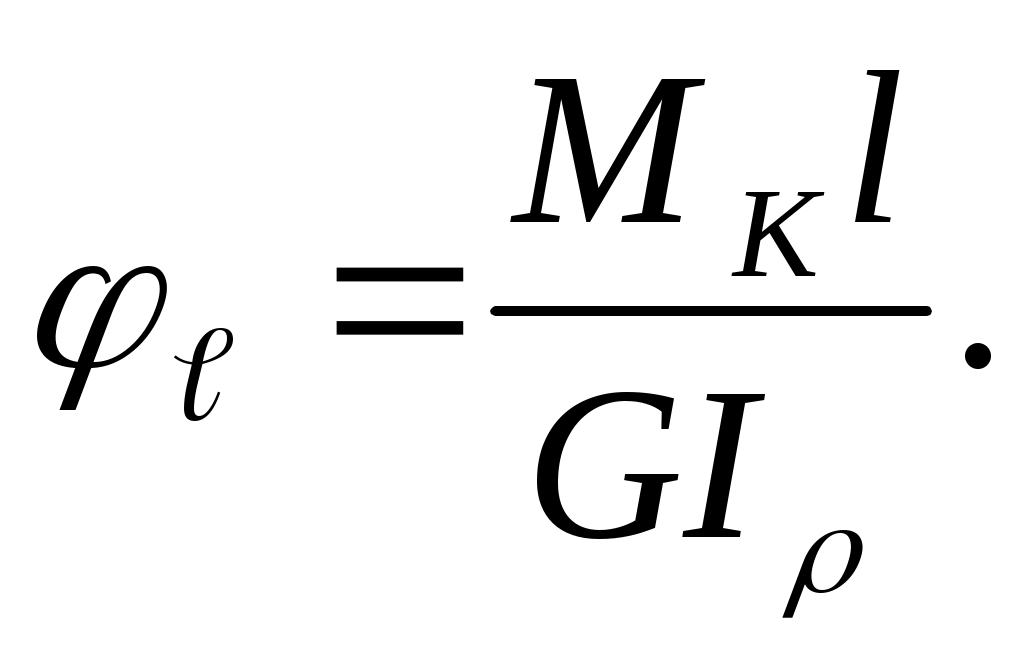 (6.6)
(6.6)
Для ступенчатых стержне и стержней, у которых МКменяется по длине на каждом участке, угол закручивания между начальным и конечным сечениями стержня подсчитывается как сумма углов закручивания по участкам с постоянным МК /I
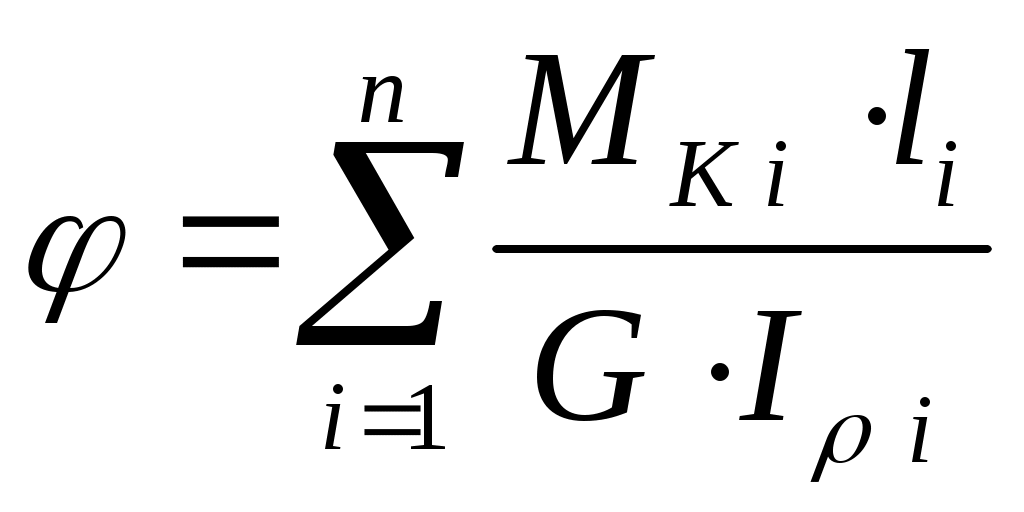 . (6.7)
. (6.7)
Полный угол закручивания не всегда может характеризовать жесткость стержня при кручении. Для оценки жесткости вводится – относительный угол закручивания, угол закручивания, приходящийся на единицу длины
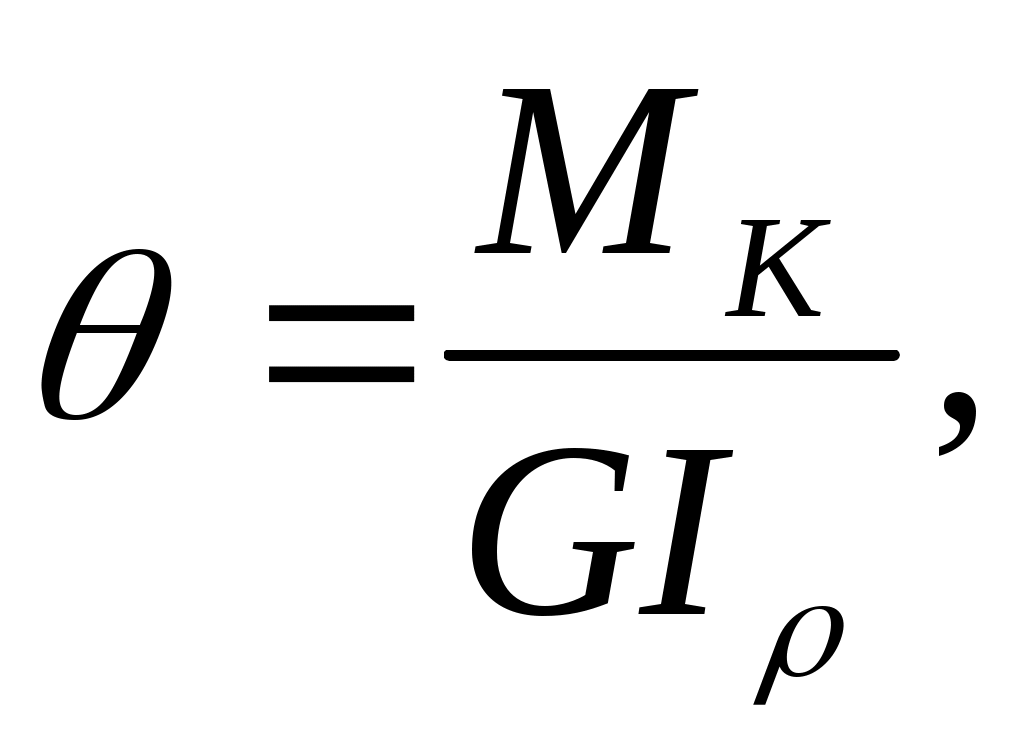 (6.8)
(6.8)
имеющий размерность рад/м, или 1/м.
6.2. Потенциальная энергия при кручении круглого вала
Будем считать, что материал стержня при кручении работает при напряжениях, не превышающих предел упругости. В этом случае работа внешних сил
А, затрачиваемая на кручение стержня, равна количеству потенциальной энергии U, накопленной в стержне:
 А = U.
А = U.
Работа А равна площади диаграммы кручения (см. рис. 6.3.):
А = U=0.5МК (6.9)
где МК крутящий момент;
угол закручивания стержня.
Подставим в формулу (9) вместо или МК их значения, тогда
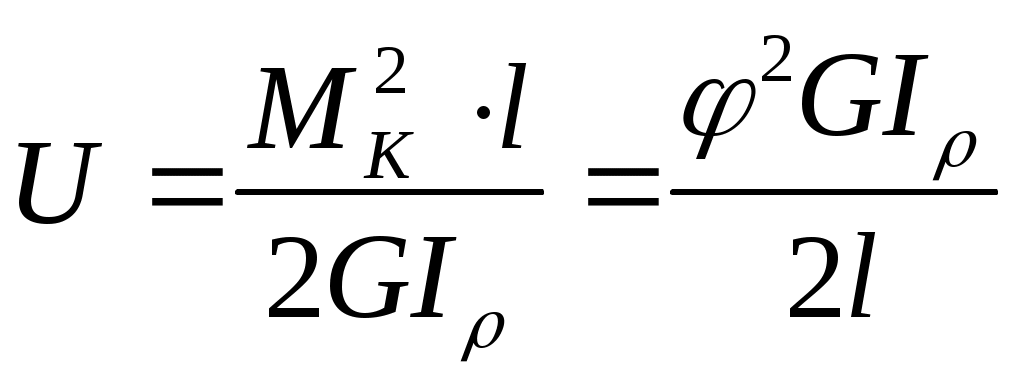 . (6.10)
. (6.10)
Формулы (6.9) и (6.10) можно пользоваться при ступенчатом изменении крутящих моментов и жесткости стержня. В этом случае потенциальная энергия равна сумме потенциальных энергий, найденных по участкам с постоянным МК /I.
Равенство А = Uчасто используют при проверке решения задачи.
Главные напряжения и главные площадки
Выше было установлено, что в поперечном сечении круглого стержня при кручении возникают касательные напряжения.
На основании закона парности касательных напряжений они возникают также и в продольных сечениях (см. рис.6.4.). Нормальные напряжения, как в поперечных, так и в продольных сечениях равны нулю. Вдоль радиуса касательные напряжения также отсутствуют. Если бы эти касательные напряжения имели место, то по закону парности такие же по величине касательные напряжения возникали бы по боковой поверхности, чего на самом деле их нет т.к. им нечему противодействовать(=0).
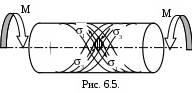
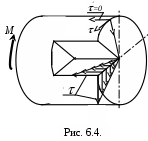
Таким образом, на двух взаимно перпендикулярных сечениях, действуют только касательные напряжения. Такое напряженное состояние называется чистым сдвигом. Из свойств этого напряженного состояния следует, что главные площадки наклонены под углом 450 к оси стержня. На этих площадках действуют главные растягивающие или сжимающие нормальные напряжения. Траектория этих напряжений представляет винтовую линию, наклоненную под углом 450 к образующей цилиндрической поверхности вала (см. 6.5.). По величине главные напряжения 1 и 3 во всех точках сечения равны касательным напряжениям .
Наибольшие по величине касательные и главные напряжения действуют в окрестностях точек, расположенных в непосредственной близости от внешней поверхности вала. Эти напряжения можно определить по формуле
Напряжение Т - предел текучести при сдвиге, который сменяется стадией упрочнения (некоторым повышением напряжений с ростом сдвигов). Для многих материалов величина Тсвязана с пределом текучести при растяжении Т соотношением
_
ТТ
5.4. Потенциальная энергия при чистом сдвиге
При деформации элемента, показанного на рис. 5.5,а), работу совершает только касательная сила Т, приложенная к верхней грани на перемещении . Сдвиг в пределах закона Гука пропорционален силе Т, что показано на рис. 5.5,б). Работа этой силы А численно равна потенциальной энергии сдвига U, определяется выражением
A=U=0.5 T,
или, учитывая, что Т= а, а = а, получим
U=0.5а2 (5.6)
Удельная потенциальная энергия деформации сдвига равна
u=U/Vоб=(0.5а2)/a20.5=(0.52)/G. (5.7)

Вопросы для самопроверки
-
Что называется абсолютным и относительным сдвигом? -
Как формулируется закон Гука при сдвиге? -
Какой модуль упругости больше; E или G? -
Чему равно изменение объёма материала при чистом сдвиге?
6. Кручение
Кручением называют такой случай деформации стержня, при котором в его поперечных сечениях возникают только одни крутящие моменты; нормальная сила, изгибающие моменты и поперечные силы равны нулю.
Исследования показали, что характер деформации скручиваемого стержня в значительной степени зависит от формы его поперечного сечения. Среди стержней с различными формами поперечного сечений, подвергаемых кручению, особое место занимают стержни с круглым или кольцевым сечением, имеющие наибольшее распространение в технике.
Круглые стержни, работающие на кручение, механики называют валами.
Ранее мы уже познакомились, c методом сечений (РОЗУ ), с вычислением крутящих моментов (МК=МZ=Т) и построением их эпюр. Для бруса постоянного сечения наиболее опасным является сечение, в котором крутящий момент имеет наибольшее абсолютное значение.
6.1. Напряжения и деформации при кручении стержня с круглым поперечным сечением
Статическая сторона задачи.
Зная величину крутящего момента в том или ином сечении, представим его статическим уравнением
где - касательное напряжение, действующее на элементарной площадке dA, расположенной от центра сечения на расстоянии произвольного радиуса .
Пока это уравнение решить нельзя т.к. неизвестен закон распределения напряжении по сечению. Рассмотрим стержень радиуса r, заделанного одним концом, на свободном конце которого приложим пару сил с моментом М.
Геометрическая сторона задачи.
Нанесем на боковую поверхность скручиваемого стержня ортогональную сетку (см.рис. 6.1,а). Оказывается, что после закручивания прямоугольники, образованные сеткой, перекашиваются, ось стержня остаётся прямолинейной, контуры поперечных сечений (круглые и плоские до деформации) остаются такими же и после деформации. При кручении происходит поворот одного сечения относительно другого на некоторый угол , называемый углом закручивания. Расстояние между поперечными сечениями практически не меняются, а это значит, что продольные волокна не удлиняются и не укорачиваются.
Описанные наблюдения характеризуют деформации волокон, лежащих на поверхности стержня, но не позволяют делать какие-либо заключения о деформации внутренних волокон. Для того чтобы сделать задачу вполне определённой, сформулируем гипотезы, которые положим в основу дальнейших выводов.
Будем предполагать, что:
1) сечения плоские до закручивания, остаются плоскими и после закручивания;
-
радиусы, проведённые мысленно в любом поперечном сечении, в процессе кручения не искривляются.
На основании принятых гипотез кручение круглого стержня можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения.

Рассмотрим (см. рис. 6.1,б) элемент стержня радиусом r, длиной dz с крутящим моментом МK.
Образующая АВ отклонится на малый угол и перейдет в положение АВ1. Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством
ВВ1 АВ
rddz.
Для произвольного волокна, отстоящего от центра стержня на расстоянии будет иметь
СС1 DC(ddz).
Физическая сторона задачи.
На основании закона Гука при сдвиге для двух указанных точек можно записать:
G=G(d dz)r; (6.2)
G=G(d dz). (6.3)
Сопоставляя формулы (6.2) и (6.3), замечаем, что касательные напряжения в точках поперечного сечения изменяются пропорционально расстоянию этих точек от оси стержня. Наибольшие напряжения наблюдаются в точках, наиболее удалённых от центра стержня. Представим графически закон распределения касательных напряжении для стержней круглого на рис. 6.2,а) и кольцевого сечения на рис. 6.2,б). По закону парности касательных напряжений касательные напряжения в каждой точке перпендикулярны радиусу и действуют не только в поперечных сечения стержня, но и в продольных.
В

ыделим вокруг произвольной точки площадку dA, на которой будет действовать элементарная касательная сила dA. Момент этой силы относительно оси стержня равен
dMKdA.
Суммируя элементарные моменты, найдём полный крутящий момент:
т.е. получим формулу (6.1).
Подставляя в (6.1) вместо его значение из (6.3), получим
Вынесем за знак интеграла величину G(ddz), т.к. для всех точек поперечного сечения она одинакова, а также заметим, что 2dA=I представляет собой полярный момент инерции сечения. Тогда
МК=GI(ddz),
или (МК /GI)=(ddz), Подставляя полученное в (6.3) найденное выражение (ddz), и тогда окончательно получим
Эта формула позволяет определить в любой точке круглого поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле
Величину W=(r) называют полярным моментом сопротивления
Полярный момент инерции для сплошного круглого сечения
r4d4
для кольцевого сечения с внешним диаметром D и внутренним d
(D4 ) (1-4)
где d / D.
Следовательно, моменты сопротивления имеют следующие значения:
для сплошного сечения Wr3d3 16
для кольцевого сечения W (D3 16) (1-4 ).
При определении угла закручивания () воспользуемся уравнением (а), из которого находим
После интегрирования получим полный угол закручивания стержня на участке
Величину GI называют жёсткостью стержня при кручении. Она характеризует сопротивление стержня закручиванию.
Если по всей длине стержня момент не меняется и стержень имеет постоянный диаметр, интегрируя выражение (6.5), получим
Для ступенчатых стержне и стержней, у которых МКменяется по длине на каждом участке, угол закручивания между начальным и конечным сечениями стержня подсчитывается как сумма углов закручивания по участкам с постоянным МК /I
Полный угол закручивания не всегда может характеризовать жесткость стержня при кручении. Для оценки жесткости вводится – относительный угол закручивания, угол закручивания, приходящийся на единицу длины
имеющий размерность рад/м, или 1/м.
6.2. Потенциальная энергия при кручении круглого вала
Будем считать, что материал стержня при кручении работает при напряжениях, не превышающих предел упругости. В этом случае работа внешних сил
А, затрачиваемая на кручение стержня, равна количеству потенциальной энергии U, накопленной в стержне:
 А = U.
А = U.Работа А равна площади диаграммы кручения (см. рис. 6.3.):
А = U=0.5МК (6.9)
где МК крутящий момент;
угол закручивания стержня.
Подставим в формулу (9) вместо или МК их значения, тогда
Формулы (6.9) и (6.10) можно пользоваться при ступенчатом изменении крутящих моментов и жесткости стержня. В этом случае потенциальная энергия равна сумме потенциальных энергий, найденных по участкам с постоянным МК /I.
Равенство А = Uчасто используют при проверке решения задачи.
-
Анализ напряженного состояния при кручении.
Главные напряжения и главные площадки
Выше было установлено, что в поперечном сечении круглого стержня при кручении возникают касательные напряжения.
На основании закона парности касательных напряжений они возникают также и в продольных сечениях (см. рис.6.4.). Нормальные напряжения, как в поперечных, так и в продольных сечениях равны нулю. Вдоль радиуса касательные напряжения также отсутствуют. Если бы эти касательные напряжения имели место, то по закону парности такие же по величине касательные напряжения возникали бы по боковой поверхности, чего на самом деле их нет т.к. им нечему противодействовать(=0).
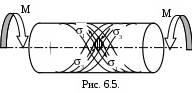

Таким образом, на двух взаимно перпендикулярных сечениях, действуют только касательные напряжения. Такое напряженное состояние называется чистым сдвигом. Из свойств этого напряженного состояния следует, что главные площадки наклонены под углом 450 к оси стержня. На этих площадках действуют главные растягивающие или сжимающие нормальные напряжения. Траектория этих напряжений представляет винтовую линию, наклоненную под углом 450 к образующей цилиндрической поверхности вала (см. 6.5.). По величине главные напряжения 1 и 3 во всех точках сечения равны касательным напряжениям .
Наибольшие по величине касательные и главные напряжения действуют в окрестностях точек, расположенных в непосредственной близости от внешней поверхности вала. Эти напряжения можно определить по формуле