Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 405
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
0+900, по которым действуют главные напряжения.
то дно, что прикаком -либо есть величина постоянная:
Для определения величины главных напряжений подставим в формулу (4.2) =0. Вынося cos20 за скобку, получим
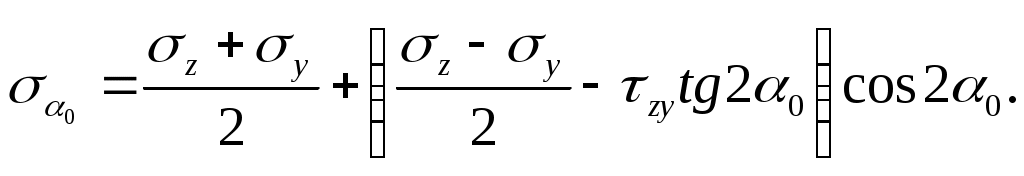 (а)
(а)
По известной из тригонометрии формуле, используя выражение (4.7), находим
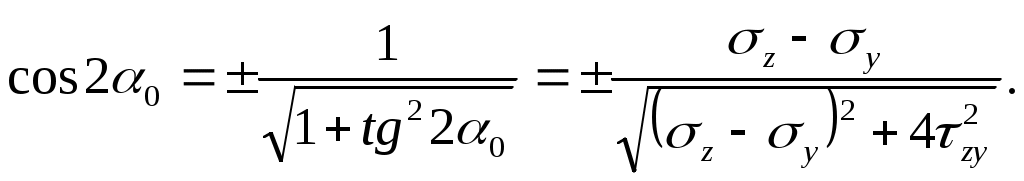 (б)
(б)
Подставляя выражение (4.7) и (б) в формулу (а) найдем два значения o, обозначаемые 1= max и 3= min:
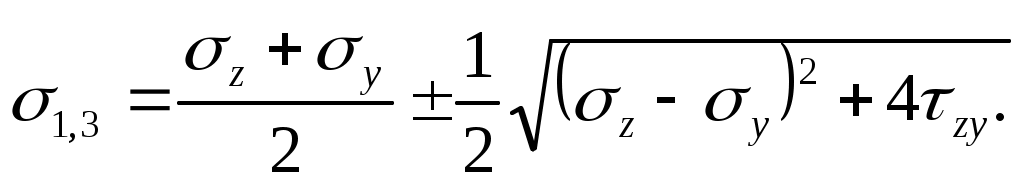 (4.8)
(4.8)
В этой формуле знак плюс соответствует максимальному главному напряжению 1= max, а минус – минимальному 3= min (принято 1 >3>3).
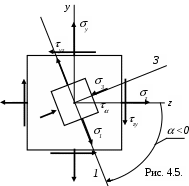 Из приведенного вывода следует, что при любых исходных напряжениях
Из приведенного вывода следует, что при любых исходных напряжениях
z, y, zy в данной точке существует параллелепипед, на гранях которого действуют только нормальные напряжения. Другими словами, плоское напряженное состояние в точке путем поворота осей всегда может быть представлено через главные напряжения (рис. 4.5.).
Можно получить формулу, определяющую тангенс одиночного угла наклона нормали главной площадки 1 или 3. Для этого предположим, что наклонная площадка на рис.4.3. – главная. Тогда проектируя все силы, действующие на призму, на вертикаль, получим
1,3 dAsin1,3-y dAy+z y dAz=0.
Отсюда, учитывая равенства (4.1), найдем
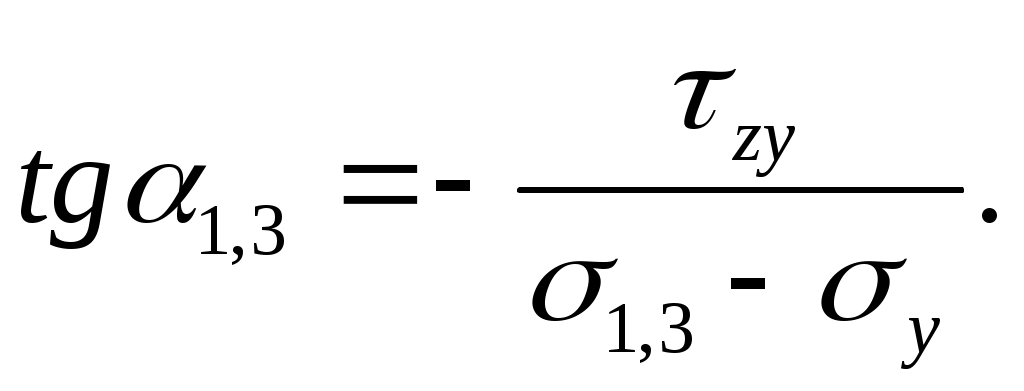 (4.9)
(4.9)
Так как касательные напряжения на главных площадках отсутствуют, то главные площадки, и напряжения наиболее просто определяют напряженное состояние в точке. Поэтому примем их за исходные (рис. 4. 6, а). Отсчитывая угол
от направления 1, напишем значение и по формулам (4.2) и (4.3), полагая в них
=1 , у=2 , а zy=0;
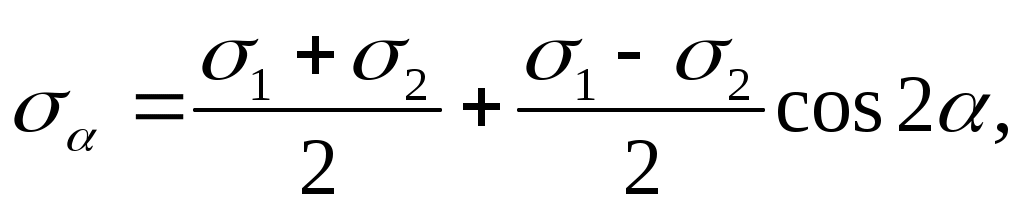 (4.10)
(4.10)
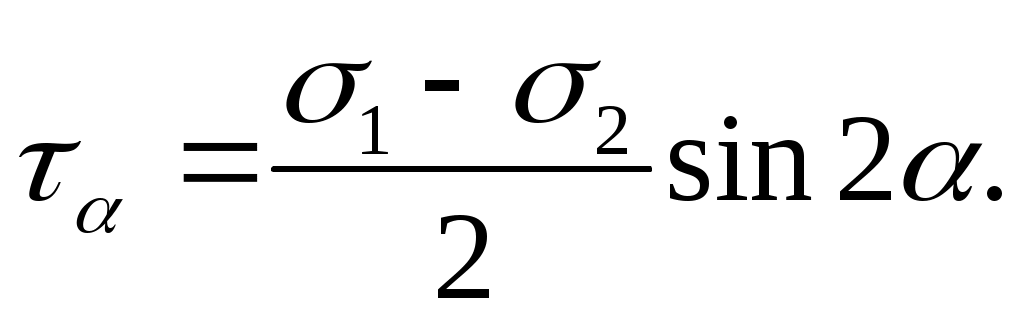 (4.11)
(4.11)
Из формулы (4.11) следует, что при =450 касательные напряжения имеют экстремальные значения
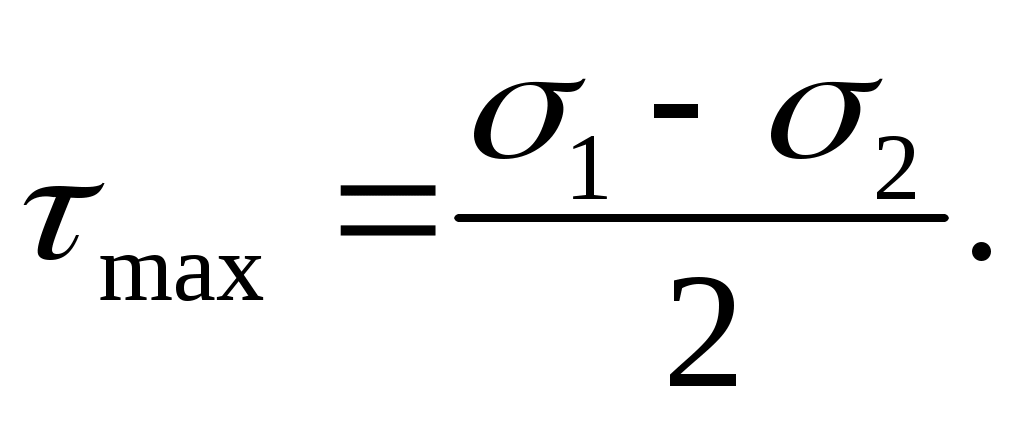 (4.12)
(4.12)
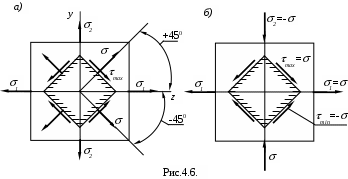
Экстремальные касательные напряжения в точке равны полуразности главных напряжений и действуют на площадках, наклоненных к главным осям под углом 450 (рис. 4. 6, а).
Подставляя выражение (8) в формулу (12), получим значение max через z, уи zy:
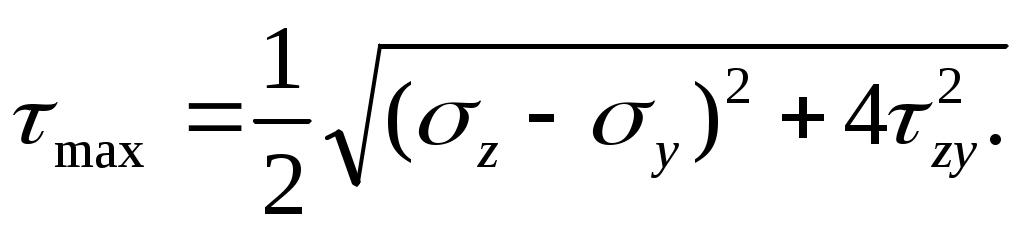 (4.13)
(4.13)
В общем случае на площадках с max нормальные напряжения не равны нулю, полагая в формуле (10) 450 и учитывая (8), получим (рис. 4.6,a)
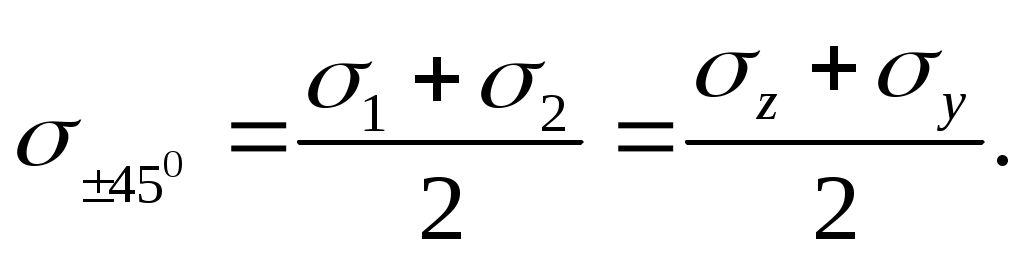 (4.14)
(4.14)
В частном случае, когда на гранях действуют два главных напряжения
1 -2 = , экстремальные касательные напряжения численно равны главным напряжениям:
max =,
а нормальные напряжения в этом случае равны нулю. Такой случай напряженного состояния носит название чистого сдвига (рис. 4.6,б).
4.1.5. Круг Мора
Зависимости напряжений и от угла наклона площадки имеют простую геометрическую интерпретацию в виде круговой диаграммы, предложенной немецким ученым Отто Мором.
Обозначим в формулах (4.10) и (4.11) постоянные величины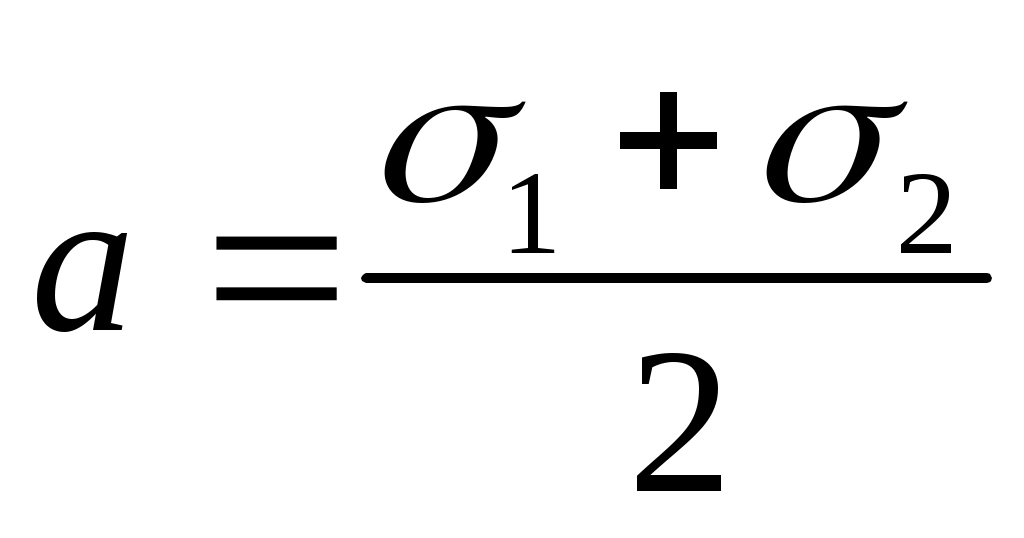 и
и 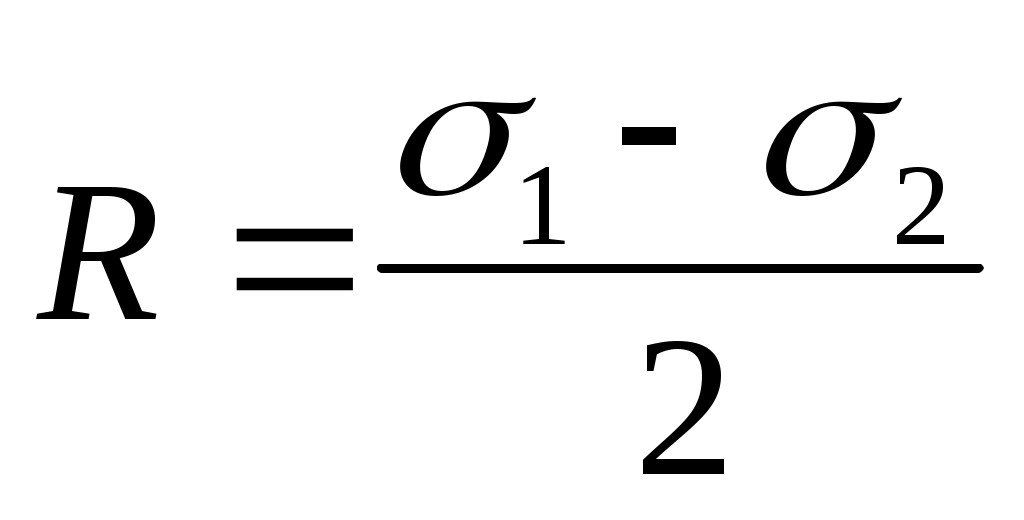 и запишем эти формулы в виде
и запишем эти формулы в виде
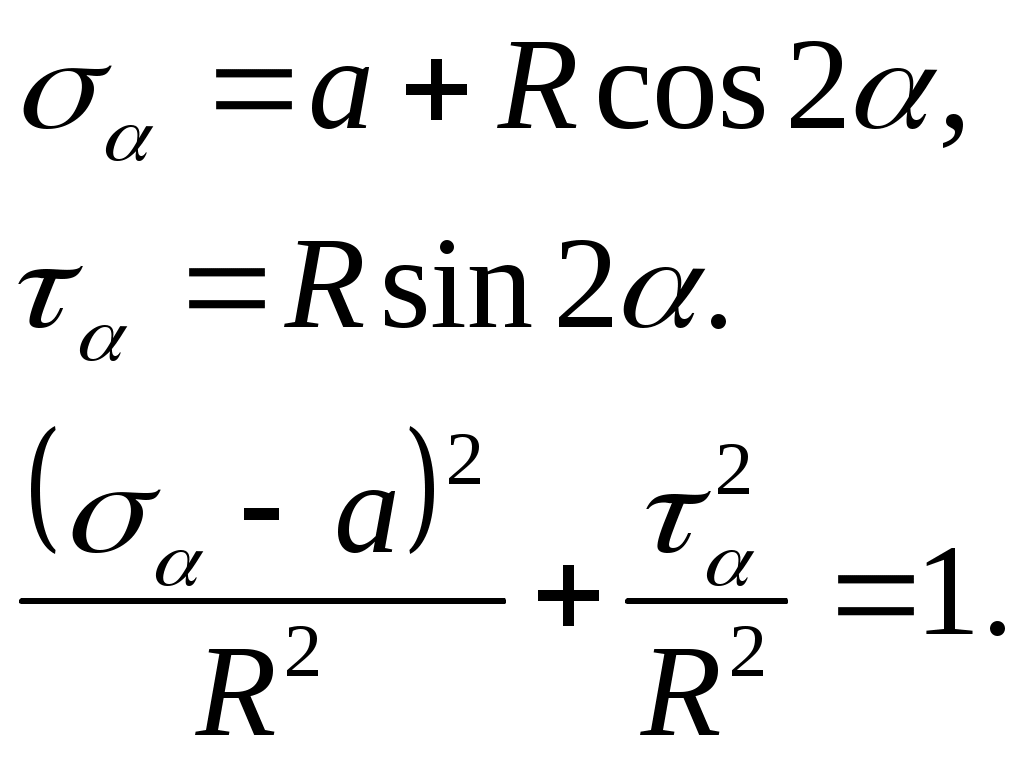 (4.15)
(4.15)
Последнее уравнение, полученное из двух первых, представляет окружность радиуса Rв координатах - (рис. 4.7, а), которая называется
к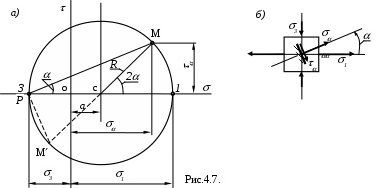
ругом Мора,
или кругом напряжений. Каждой наклонной площадке, определяемой углом (рис.4. 7, б),
на окружности соответствует некоторая точка, которую называют изображающей точкой М, координаты которой равны и . Чтобы установить соответствие между площадкой и изображающей точкой на окружности, удобно воспользоваться точкой Р- полюсом круга. Полюс круга – точка пересечения линии, исходящих из точек, отображающих на круге напряжения на ортогональных гранях элемента, и параллельных нормалям этих граней. В данном случае точка Р, совпадает с точкой 3, где пересекаются линии параллельные главным нормалям и исходящие соответственно из координат 1, 3. Следовательно, луч РМ, будет параллельным нормали наклонной площадки, и в пересечении с окружностью дает точку
М( ,.), что очевидно из чертежа. Из чертежа очевидно и то, что точка М будет отражать напряженное состояние на ортогональной площадке, а луч РМ, перпендикулярный РМ, будет параллельным нормали этой наклонной площадки, и, что отрезок ММ равен диаметру круга Мора. Тем самым, определив полюс Р, далее сможем определить напряжения на любой искомой наклонной площадке, проводя соответствующий этой наклонной площадке, параллельный нормали этой наклонной площадки луч РМ.
Пример 4.1. Определить графически главные напряжения при чистом сдвиге.
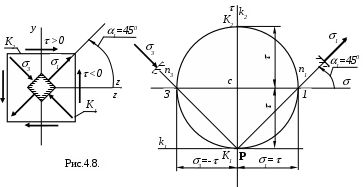
Введем обозначения К1 и К2 для любых двух ортогональных граней элемента (см. рис.4.8.). Строим в координатах ( -) по точкам К1(0,- ) и К2 (0, ) круг Мора. Центр круга Мора совпадает с началом координат (т.С). Затем через эти точки проводим прямые k1 иk2, параллельные нормалям, выбранных ортогональных граней, и получаем полюс Р. В точках 1 и 3 круга Мора нет касательных напряжений, следовательно, при чистом сдвиге главные площадки наклонены к граням элемента под углом 450. Из рис. 4.8. видно,
что1-3= .
П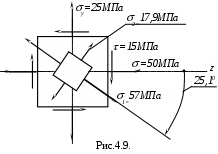 ример 4.2. Определить значение и направление главных напряжений для случая напряженного состояния, показанного на рис. 4.9.
ример 4.2. Определить значение и направление главных напряжений для случая напряженного состояния, показанного на рис. 4.9.
Р е ш е н и е. По формуле (4.7) определяем положение главных площадок, перпендикулярных плоскости чертежа:
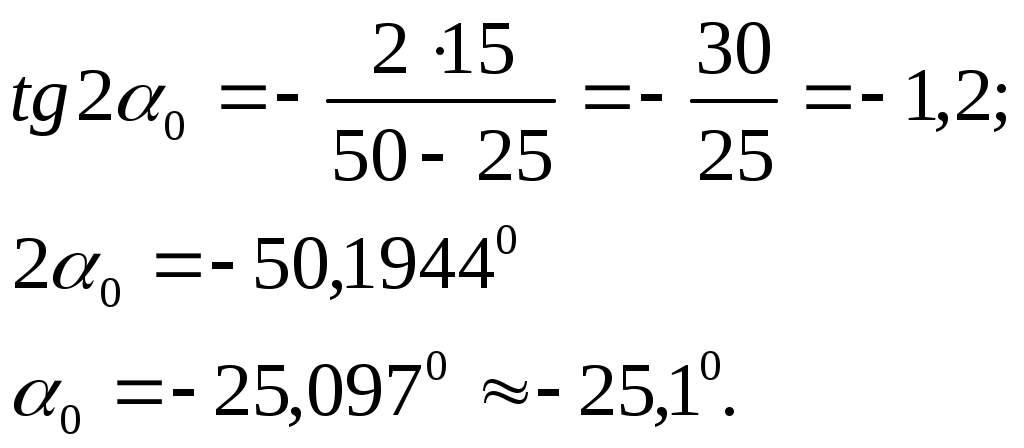
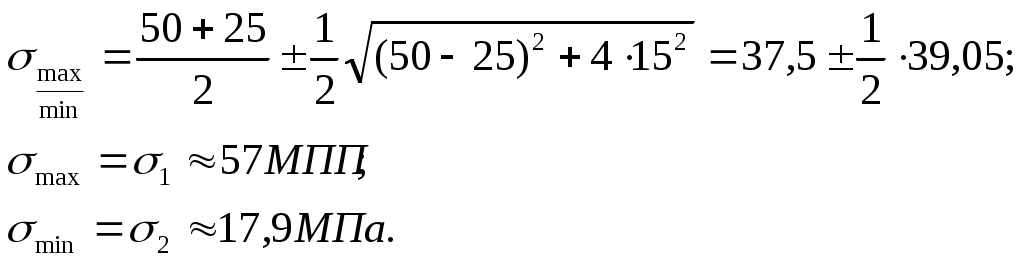
П р о в е р к а.
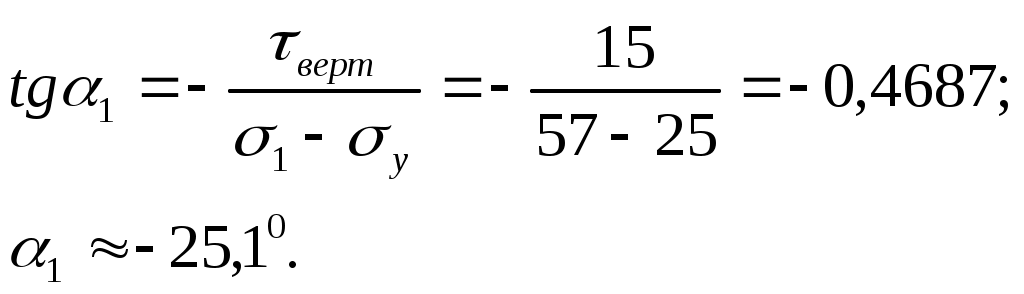
Определим графически главные напряжения по величине и направлению
(см. рис. 4.10.).
На рисунке представлен круг напряжений, изображённый по точкам исходных площадок К1(50, 15) и К2(25, -15) с нормалями k1 и k2, соответственно. Р – полюс.
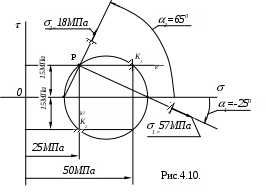
При черчение круга Мора на ПЭВМ по программе “AutoCAD “ или “Компас-график” получим расчет высокой точности.
4.2.1. Главные деформации. Удлинение в произвольном направлении
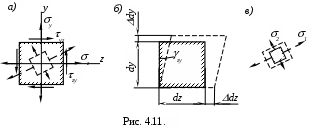
В общем случае напряженное состояние бесконечно малого элемента определяется нормальными напряжениямиz, yи касательными напряжениями
zy=yz(рис. 4.11,а). Возникновение этих напряжений сопровождается деформацией
элемента. Рассмотрим деформации элемента, развивающиеся в плоскости упомянутых напряжений.
Для изотропного материала удлинения сторон элемента связаны с действием нормальных напряжений. Обозначим их через dz и dy (рис. 4.11,б).
Линейные деформации в точке характеризуют величинами относительных удлинений в соответствующих направлениях:
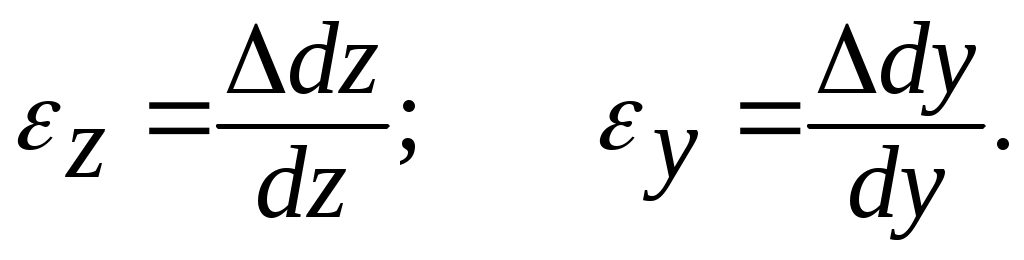 (4.16)
(4.16)
С касательными напряжениями связана угловая деформация, или деформация сдвига. Она связана в изменении первоначального прямого угла на угол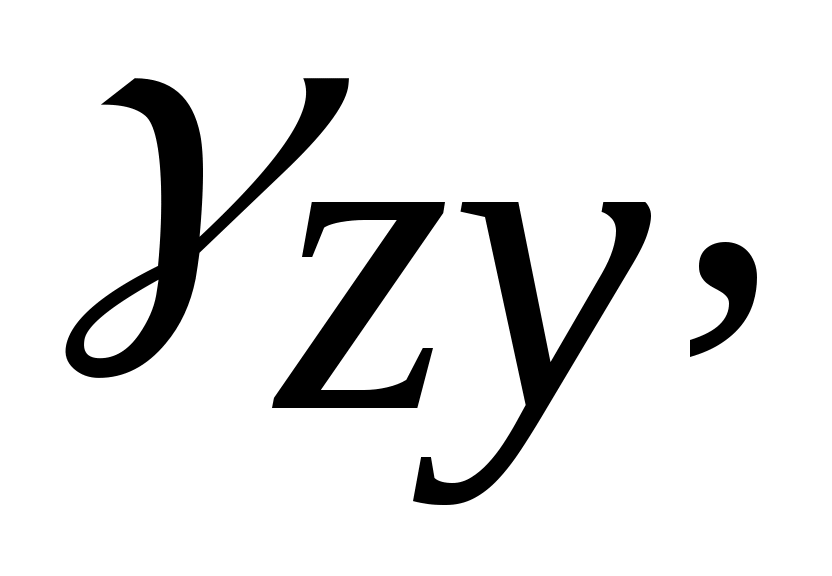 называемый углом сдвига (рис. 4.11,б).
называемый углом сдвига (рис. 4.11,б).
Каждому, вновь выбранному положению осей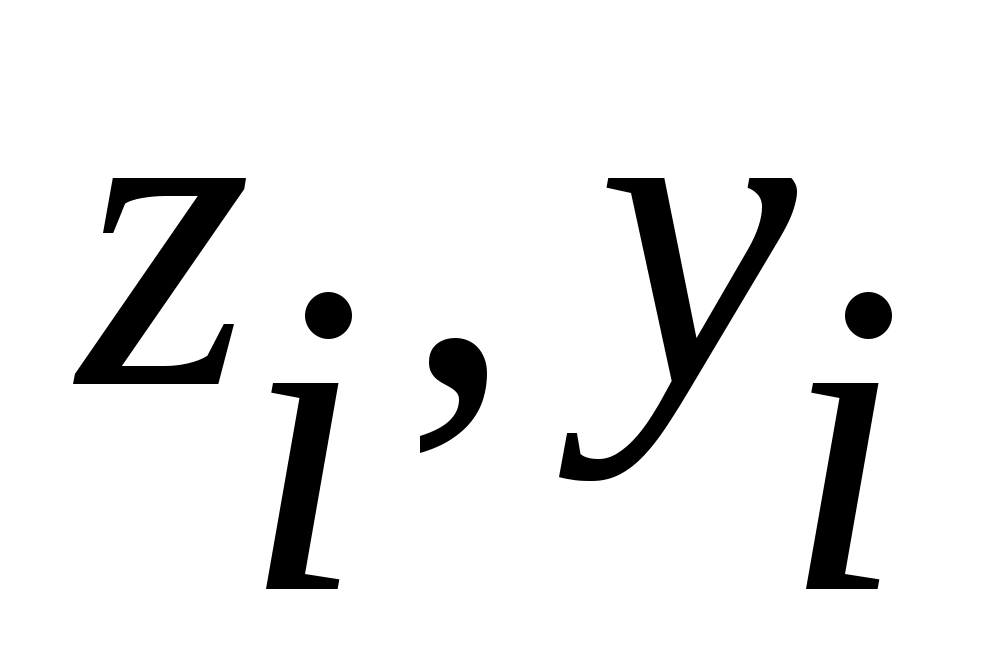
будут соответствовать свои удлинения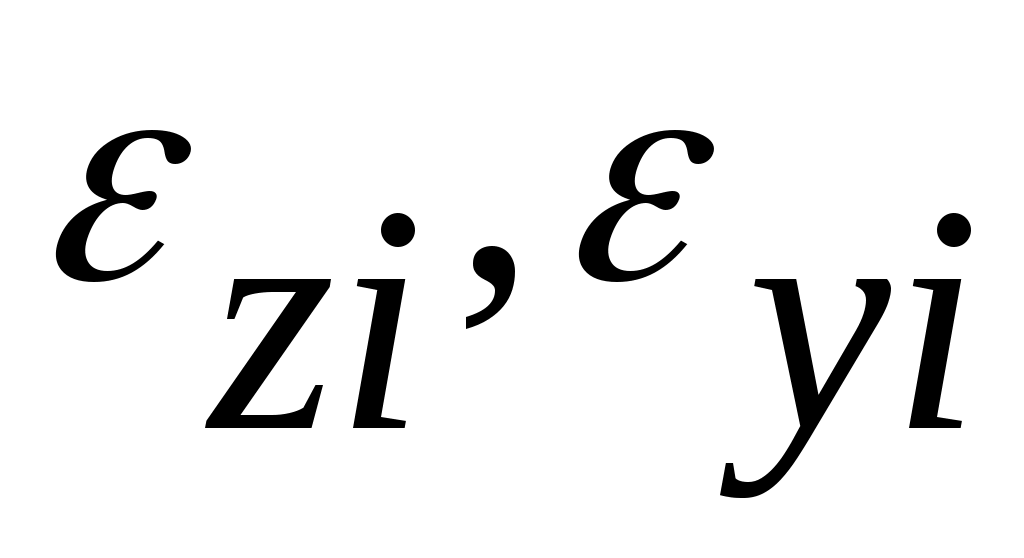 и угол сдвига
и угол сдвига 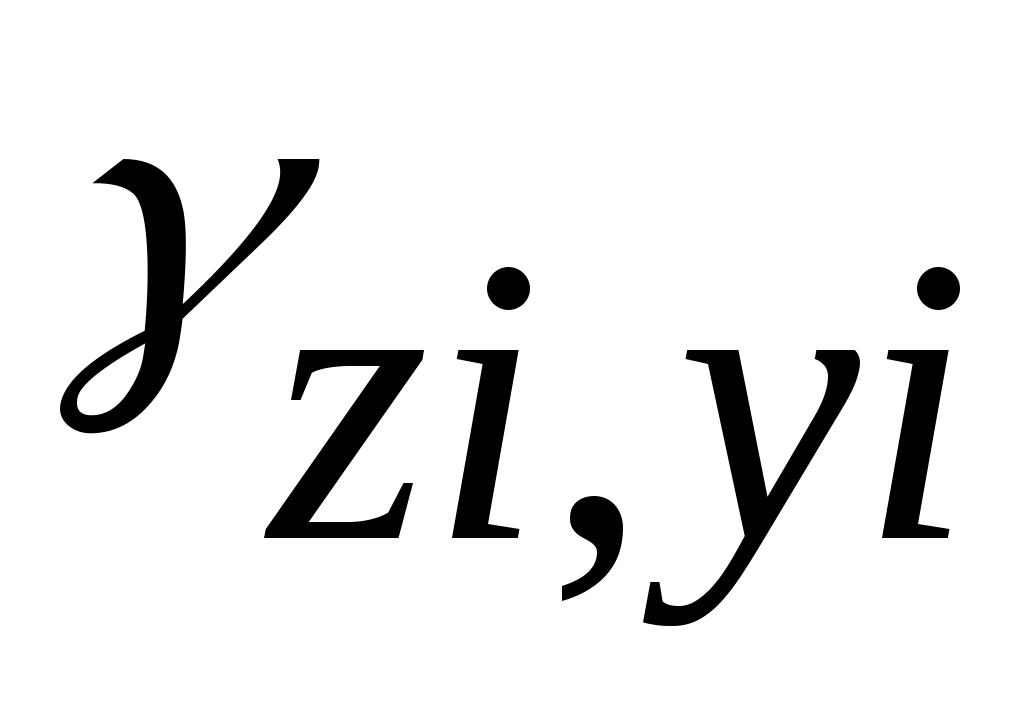 . Совокупность относительных удлинений и углов сдвига для всевозможных положений осей
. Совокупность относительных удлинений и углов сдвига для всевозможных положений осей  характеризует деформированное состояние в точке.
характеризует деформированное состояние в точке.
Так как любое плоское напряженное состояние сводиться к растяжению (сжатию) в двух взаимно перпендикулярных направлениях главными напряжениями, то прямоугольный элемент, например (рис. 4.11,в), от 1 и 2 , будет испытывать только удлинение, а угол сдвига будет равен нулю.
Относительные удлинения вдоль главных напряжений 1 и 2называются главными деформациями в данной точке, они имеют экстремальные значения по сравнению с удлинениями в любых других направлениях, исходящих из данной точки.
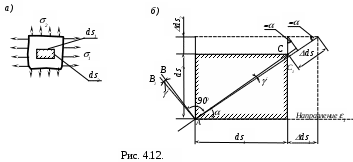
Найдём относительное удлинение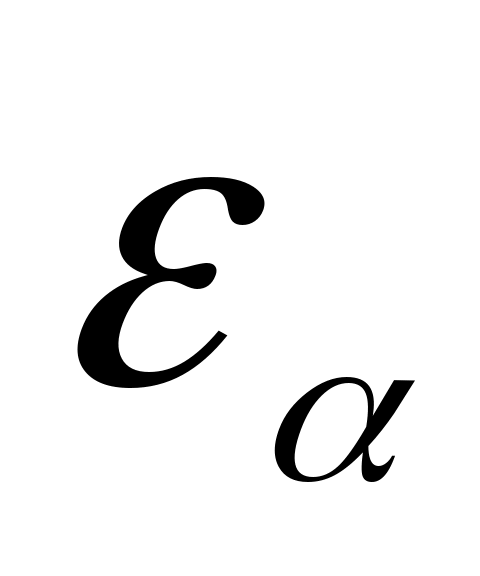 отрезка, проходящего через рассматриваемую точку под произвольным углом к направлению 1(рис. 4.12.).
отрезка, проходящего через рассматриваемую точку под произвольным углом к направлению 1(рис. 4.12.).
Будем считать главные деформации 1 и 2 заданными. Наклонный отрезок длиной ds будем рассматривать как диагональ прямоугольного элемента, выделенного из тела (рис. 4.12,а) и имеющего длину сторон ds1и ds2в направлении главных деформаций. Из чертежа (рис. 4.12,б) находим абсолютное удлинение наклонного отрезка, принимая из-за малости деформаций угол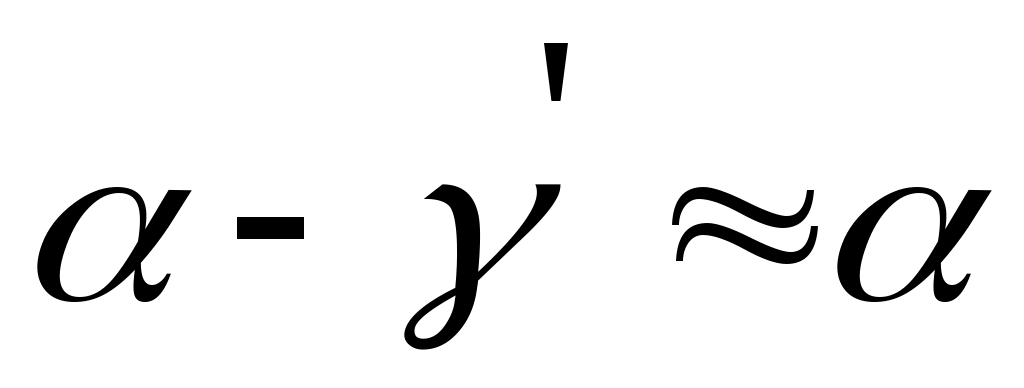 :
:
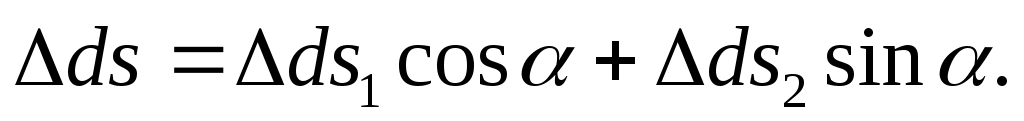
Искомое относительное удлинение равно
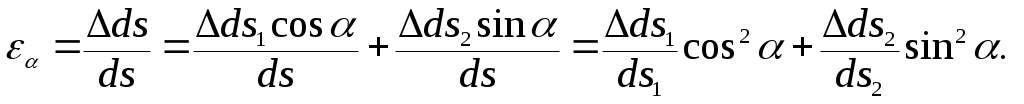
Учитывая, что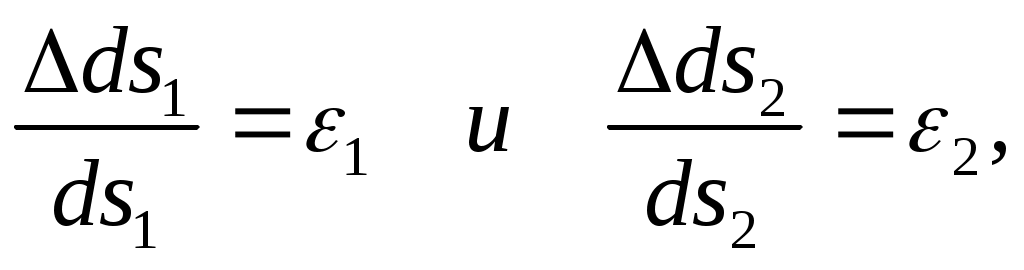
то дно, что прикаком -либо есть величина постоянная:
Для определения величины главных напряжений подставим в формулу (4.2) =0. Вынося cos20 за скобку, получим
По известной из тригонометрии формуле, используя выражение (4.7), находим
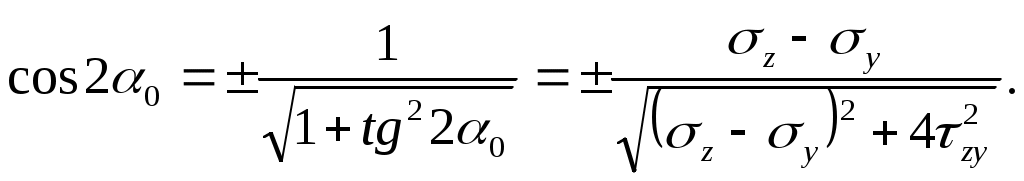 (б)
(б)Подставляя выражение (4.7) и (б) в формулу (а) найдем два значения o, обозначаемые 1= max и 3= min:
В этой формуле знак плюс соответствует максимальному главному напряжению 1= max, а минус – минимальному 3= min (принято 1 >3>3).
 Из приведенного вывода следует, что при любых исходных напряжениях
Из приведенного вывода следует, что при любых исходных напряженияхz, y, zy в данной точке существует параллелепипед, на гранях которого действуют только нормальные напряжения. Другими словами, плоское напряженное состояние в точке путем поворота осей всегда может быть представлено через главные напряжения (рис. 4.5.).
Можно получить формулу, определяющую тангенс одиночного угла наклона нормали главной площадки 1 или 3. Для этого предположим, что наклонная площадка на рис.4.3. – главная. Тогда проектируя все силы, действующие на призму, на вертикаль, получим
1,3 dAsin1,3-y dAy+z y dAz=0.
Отсюда, учитывая равенства (4.1), найдем
-
Экстремальные касательные напряжения
Так как касательные напряжения на главных площадках отсутствуют, то главные площадки, и напряжения наиболее просто определяют напряженное состояние в точке. Поэтому примем их за исходные (рис. 4. 6, а). Отсчитывая угол
от направления 1, напишем значение и по формулам (4.2) и (4.3), полагая в них
=1 , у=2 , а zy=0;
Из формулы (4.11) следует, что при =450 касательные напряжения имеют экстремальные значения

Экстремальные касательные напряжения в точке равны полуразности главных напряжений и действуют на площадках, наклоненных к главным осям под углом 450 (рис. 4. 6, а).
Подставляя выражение (8) в формулу (12), получим значение max через z, уи zy:
В общем случае на площадках с max нормальные напряжения не равны нулю, полагая в формуле (10) 450 и учитывая (8), получим (рис. 4.6,a)
В частном случае, когда на гранях действуют два главных напряжения
1 -2 = , экстремальные касательные напряжения численно равны главным напряжениям:
max =,
а нормальные напряжения в этом случае равны нулю. Такой случай напряженного состояния носит название чистого сдвига (рис. 4.6,б).
4.1.5. Круг Мора
Зависимости напряжений и от угла наклона площадки имеют простую геометрическую интерпретацию в виде круговой диаграммы, предложенной немецким ученым Отто Мором.
Обозначим в формулах (4.10) и (4.11) постоянные величины
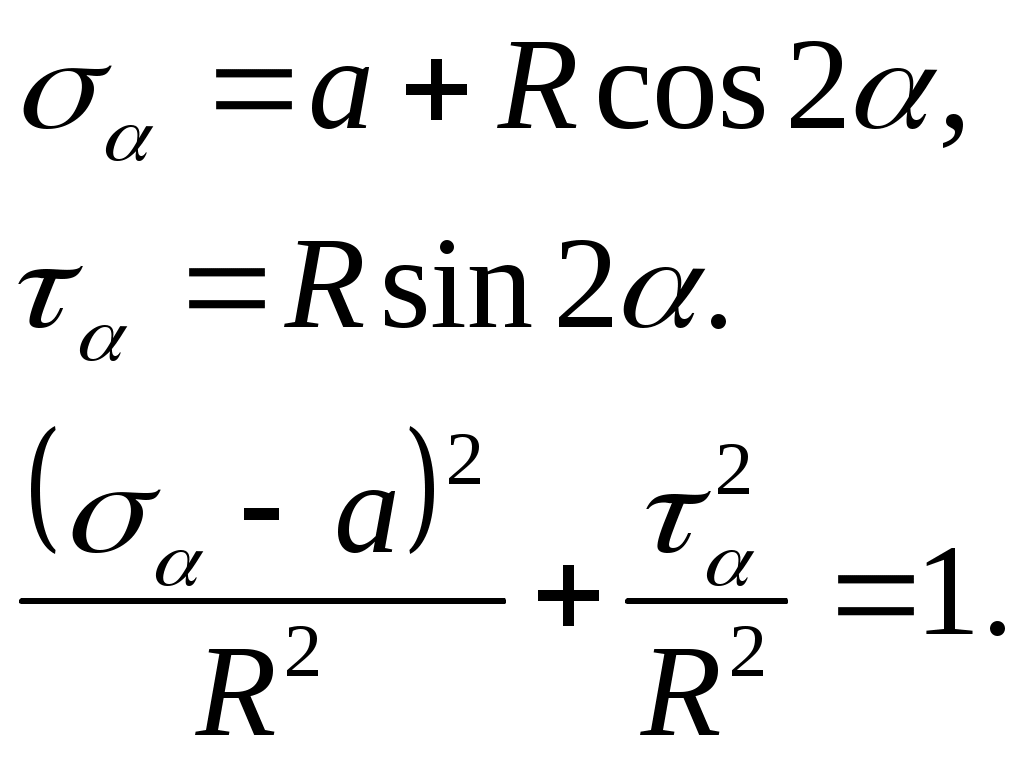 (4.15)
(4.15)Последнее уравнение, полученное из двух первых, представляет окружность радиуса Rв координатах - (рис. 4.7, а), которая называется
к

ругом Мора,
или кругом напряжений. Каждой наклонной площадке, определяемой углом (рис.4. 7, б),
на окружности соответствует некоторая точка, которую называют изображающей точкой М, координаты которой равны и . Чтобы установить соответствие между площадкой и изображающей точкой на окружности, удобно воспользоваться точкой Р- полюсом круга. Полюс круга – точка пересечения линии, исходящих из точек, отображающих на круге напряжения на ортогональных гранях элемента, и параллельных нормалям этих граней. В данном случае точка Р, совпадает с точкой 3, где пересекаются линии параллельные главным нормалям и исходящие соответственно из координат 1, 3. Следовательно, луч РМ, будет параллельным нормали наклонной площадки, и в пересечении с окружностью дает точку
М( ,.), что очевидно из чертежа. Из чертежа очевидно и то, что точка М будет отражать напряженное состояние на ортогональной площадке, а луч РМ, перпендикулярный РМ, будет параллельным нормали этой наклонной площадки, и, что отрезок ММ равен диаметру круга Мора. Тем самым, определив полюс Р, далее сможем определить напряжения на любой искомой наклонной площадке, проводя соответствующий этой наклонной площадке, параллельный нормали этой наклонной площадки луч РМ.
Пример 4.1. Определить графически главные напряжения при чистом сдвиге.

Введем обозначения К1 и К2 для любых двух ортогональных граней элемента (см. рис.4.8.). Строим в координатах ( -) по точкам К1(0,- ) и К2 (0, ) круг Мора. Центр круга Мора совпадает с началом координат (т.С). Затем через эти точки проводим прямые k1 иk2, параллельные нормалям, выбранных ортогональных граней, и получаем полюс Р. В точках 1 и 3 круга Мора нет касательных напряжений, следовательно, при чистом сдвиге главные площадки наклонены к граням элемента под углом 450. Из рис. 4.8. видно,
что1-3= .
П
 ример 4.2. Определить значение и направление главных напряжений для случая напряженного состояния, показанного на рис. 4.9.
ример 4.2. Определить значение и направление главных напряжений для случая напряженного состояния, показанного на рис. 4.9.
Р е ш е н и е. По формуле (4.7) определяем положение главных площадок, перпендикулярных плоскости чертежа:
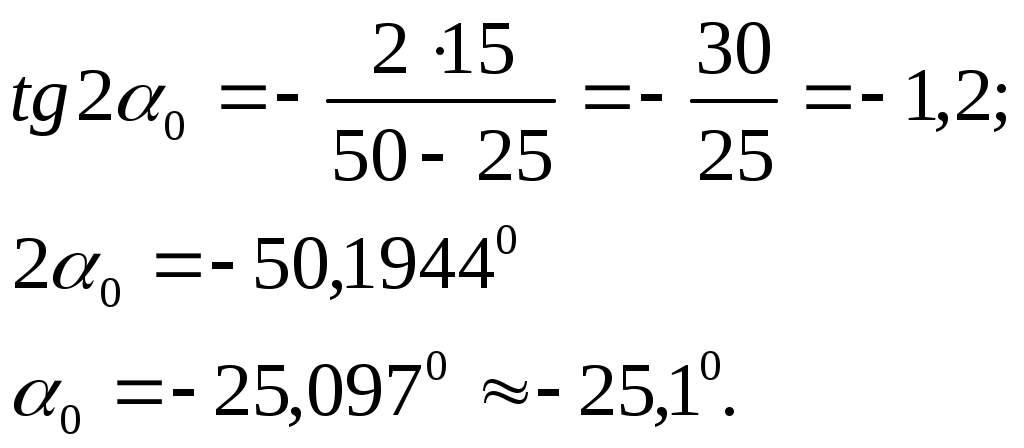
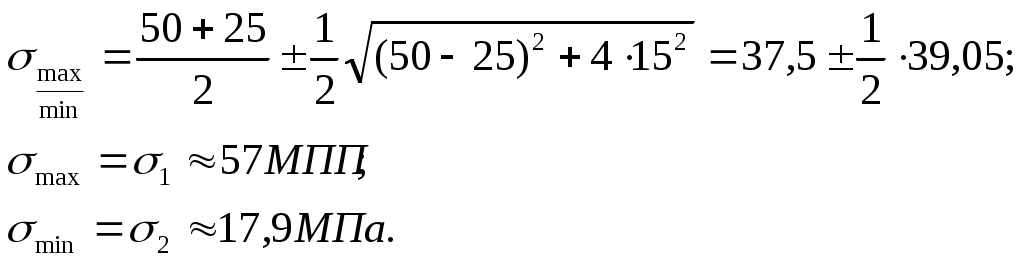
П р о в е р к а.
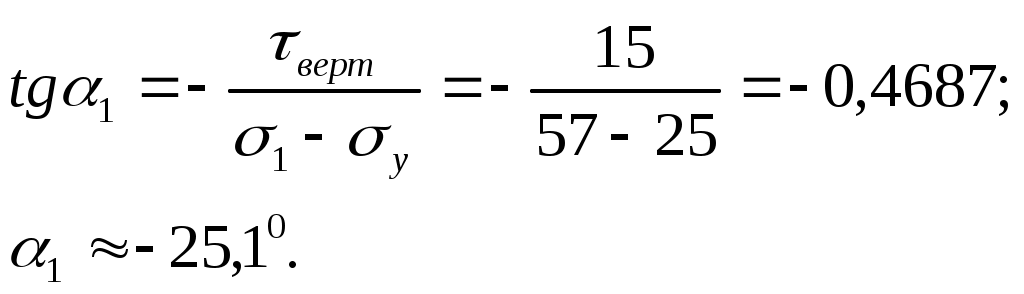
Определим графически главные напряжения по величине и направлению
(см. рис. 4.10.).
На рисунке представлен круг напряжений, изображённый по точкам исходных площадок К1(50, 15) и К2(25, -15) с нормалями k1 и k2, соответственно. Р – полюс.

При черчение круга Мора на ПЭВМ по программе “AutoCAD “ или “Компас-график” получим расчет высокой точности.
-
Деформированное состояние в точке
4.2.1. Главные деформации. Удлинение в произвольном направлении
В общем случае напряженное состояние бесконечно малого элемента определяется нормальными напряжениямиz, yи касательными напряжениями
zy=yz(рис. 4.11,а). Возникновение этих напряжений сопровождается деформацией
элемента. Рассмотрим деформации элемента, развивающиеся в плоскости упомянутых напряжений.
Для изотропного материала удлинения сторон элемента связаны с действием нормальных напряжений. Обозначим их через dz и dy (рис. 4.11,б).

Линейные деформации в точке характеризуют величинами относительных удлинений в соответствующих направлениях:
С касательными напряжениями связана угловая деформация, или деформация сдвига. Она связана в изменении первоначального прямого угла на угол
Каждому, вновь выбранному положению осей
будут соответствовать свои удлинения
Так как любое плоское напряженное состояние сводиться к растяжению (сжатию) в двух взаимно перпендикулярных направлениях главными напряжениями, то прямоугольный элемент, например (рис. 4.11,в), от 1 и 2 , будет испытывать только удлинение, а угол сдвига будет равен нулю.
Относительные удлинения вдоль главных напряжений 1 и 2называются главными деформациями в данной точке, они имеют экстремальные значения по сравнению с удлинениями в любых других направлениях, исходящих из данной точки.

Найдём относительное удлинение
Будем считать главные деформации 1 и 2 заданными. Наклонный отрезок длиной ds будем рассматривать как диагональ прямоугольного элемента, выделенного из тела (рис. 4.12,а) и имеющего длину сторон ds1и ds2в направлении главных деформаций. Из чертежа (рис. 4.12,б) находим абсолютное удлинение наклонного отрезка, принимая из-за малости деформаций угол
Искомое относительное удлинение равно
Учитывая, что