Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 408
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
окончательно получим
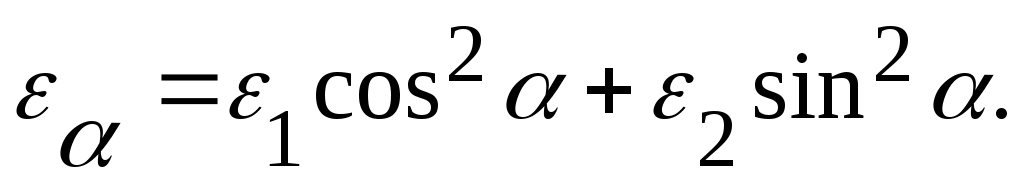 (4.17)
(4.17)
Используя равенства cos2 =0,5(1+ cos2); sin2 =0,5(1- cos2), формулу
(4.17) можно представить в следующем виде:
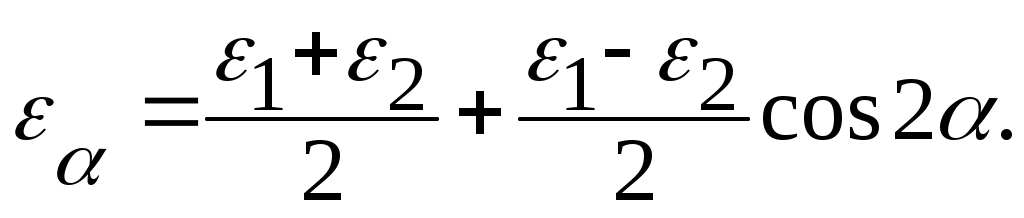
Аналогия между зависимостями для напряженного и
деформированного состояний в точке
Найдем угол сдвига между двумя взаимно перпендикулярными отрезками АС и АВ (рис. 4.12,б), расположенными под угол к направлению главной
деформации 1
Отрезок АС в результате деформации повернулся на угол :
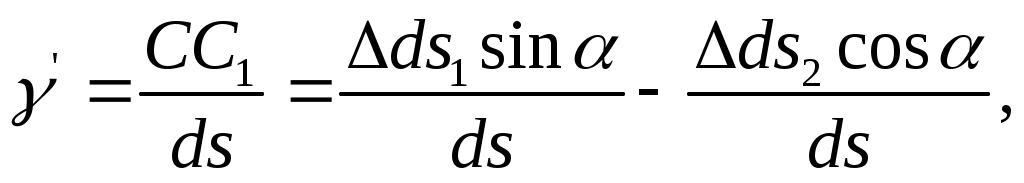
или
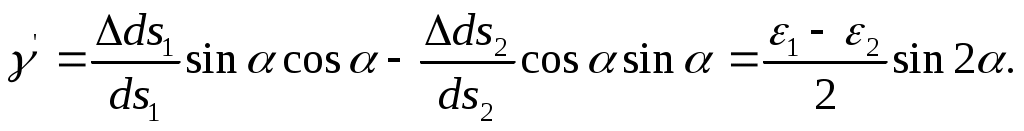 (а)
(а)
Для определения угла в формуле (а) угол надо заменить на
угол ( + 900).
Тогда получим
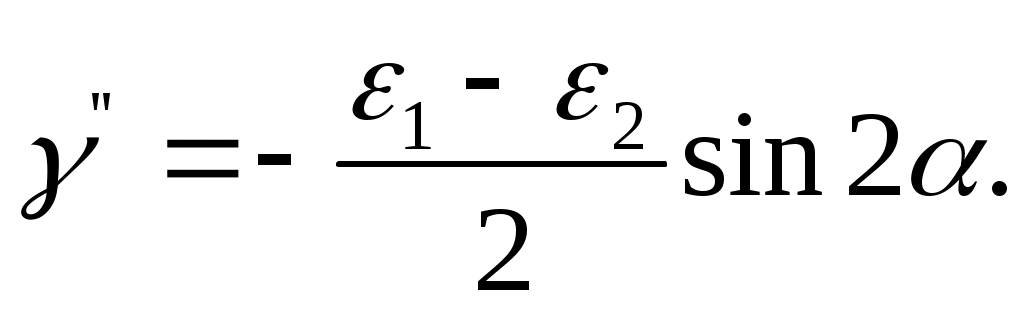 (б)
(б)
Так как прямой угол увеличился, то
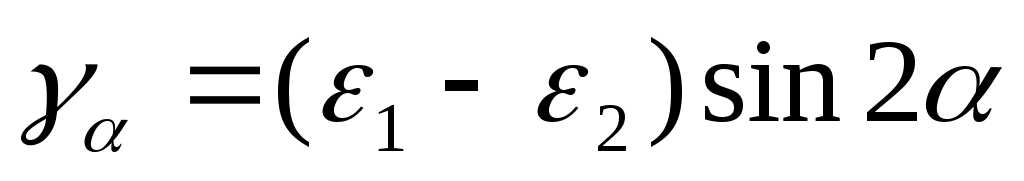 (4.18)
(4.18)
Формулы (4.17) и (4.18) запишем вместе:

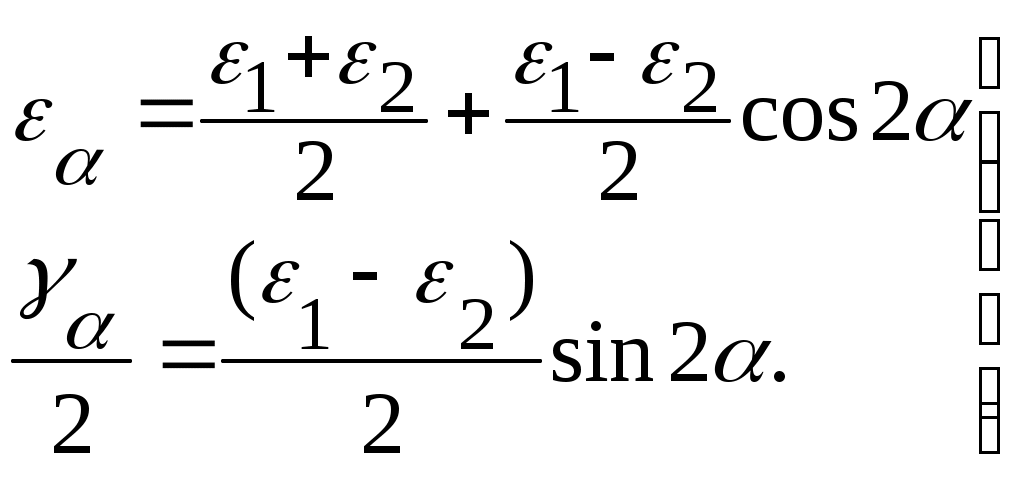 (4.19)
(4.19)
Вспомним формулы (4.10) и (4.11), описывающие напряженное состояние в точке,

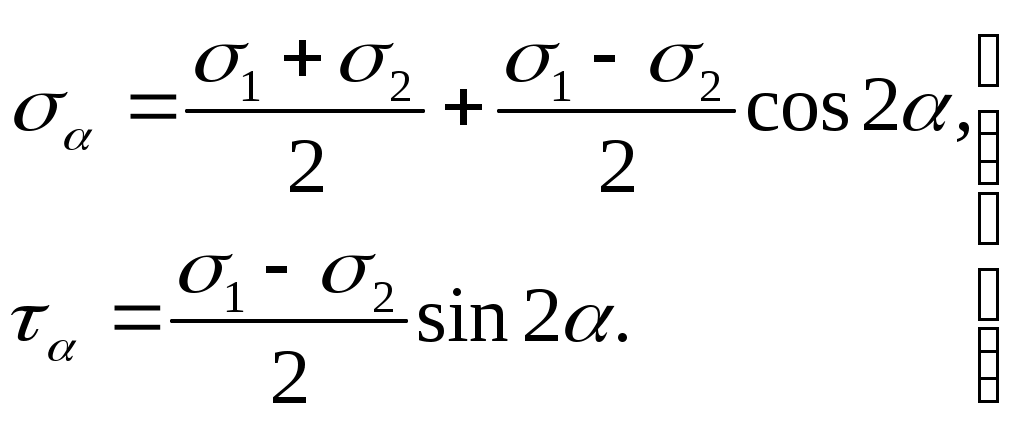 (4.20)
(4.20)
Зависимости (4.19) и (4.20) указывают на математическую аналогию законов распределения , и деформаций и ( / 2) в точке.
На основании аналогии можно без вывода записать формулу
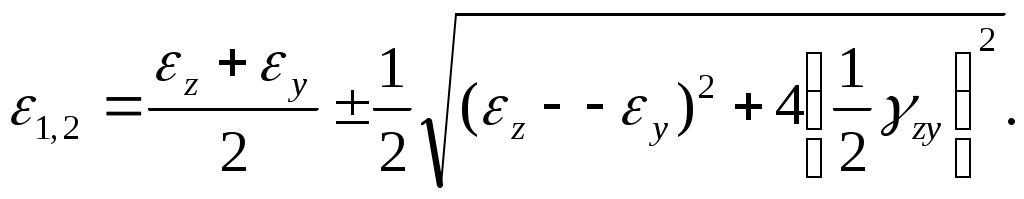 (4.21)
(4.21)
Из (4.21) следует, что
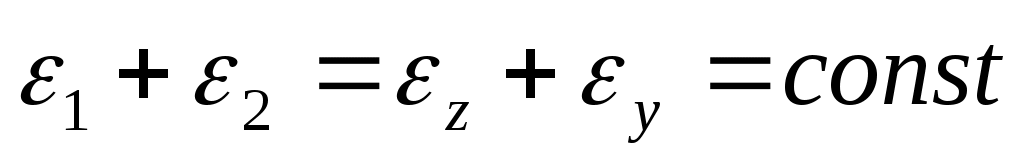 . (4.22)
. (4.22)
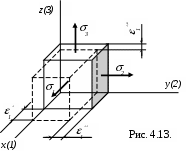
Допустим, что элемент материала в виде кубика с ребрами единичной длины растягивается нормальным усилием 1 по направлению x (1 ) (рис. 4.13.)
Относительная деформация в направление этой оси
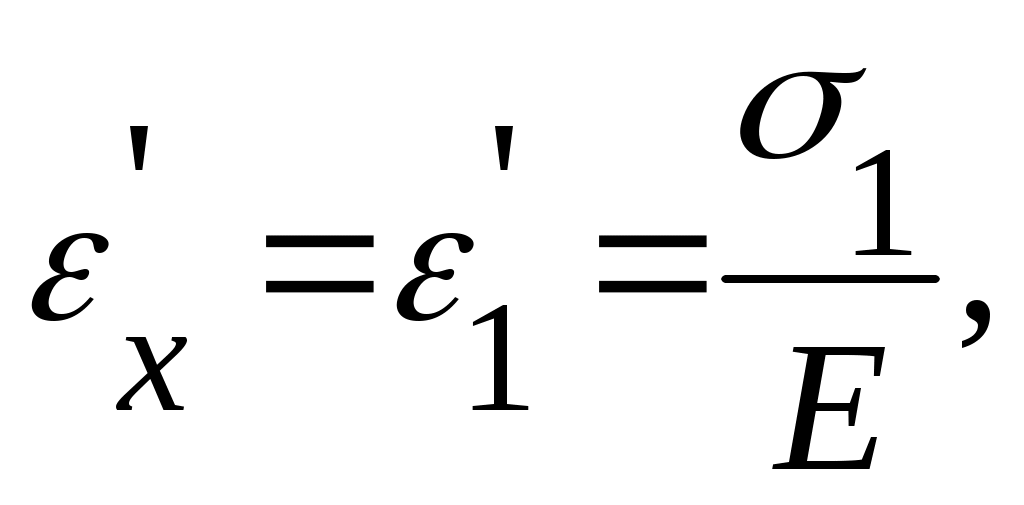
а в направлении осей y и zили 2 и 3
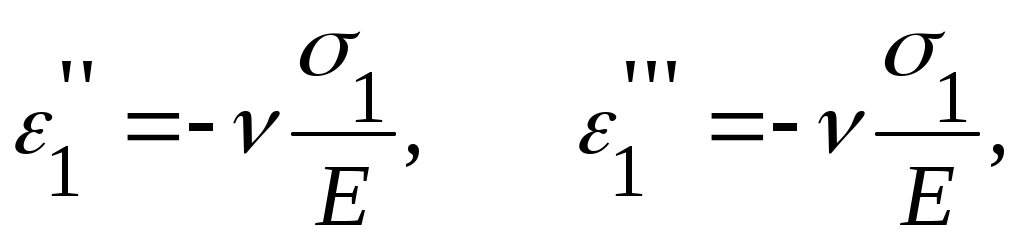
где Е - модуль продольной упругости; - коэффициент Пуассона.
По аналогии получим относительные деформации от растягивающих нормальных усилий 2 и 3 .
Следовательно,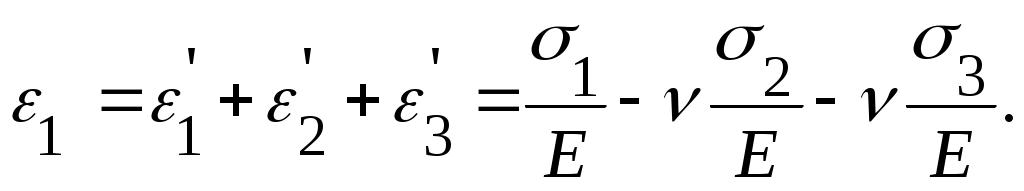
Применяя подобное рассуждение к определению 2 и 3 , получим формулу обобщенного закона Гука:
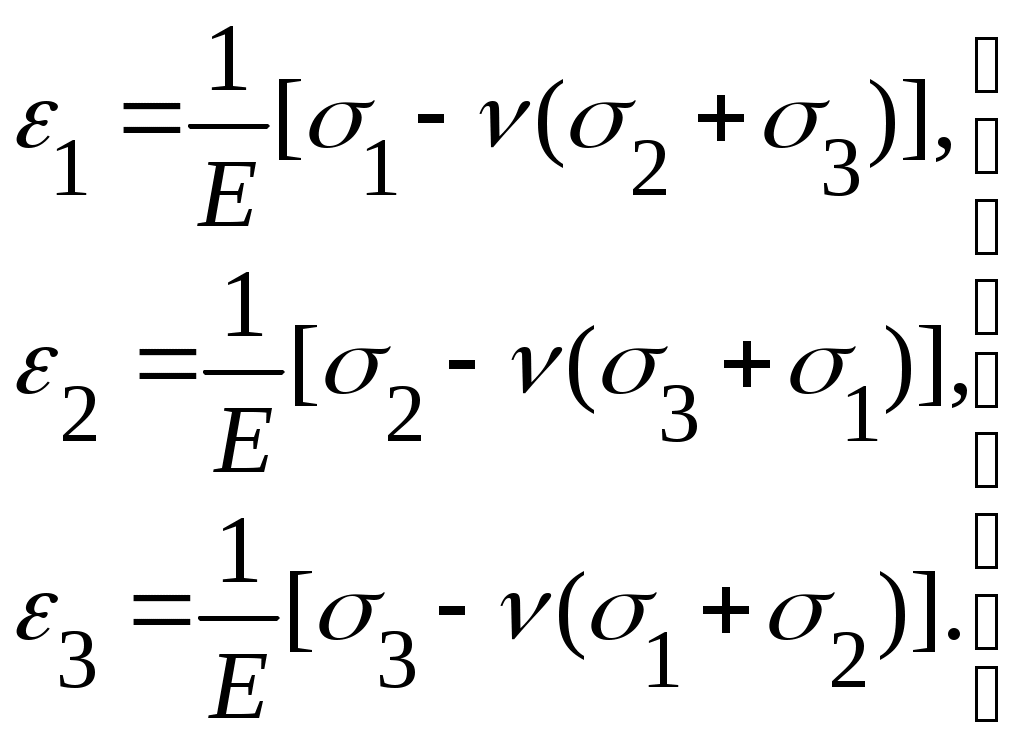 (4.23)
(4.23)
Относительной объёмной деформацией называется отношение приращения объёма к его начальному значению
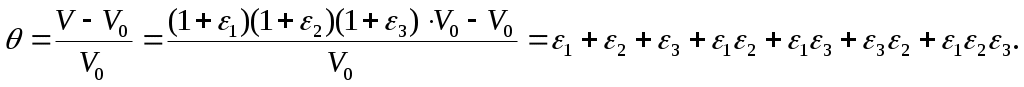
Пренебрегая произведением малых, запишем
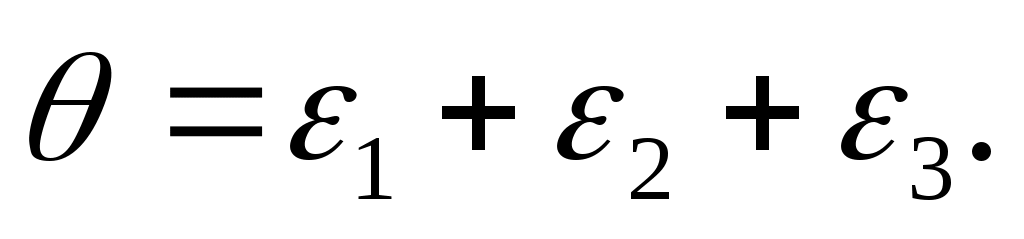 (4.24)
(4.24)
Выражая деформации через напряжения согласно формулам (21), получим
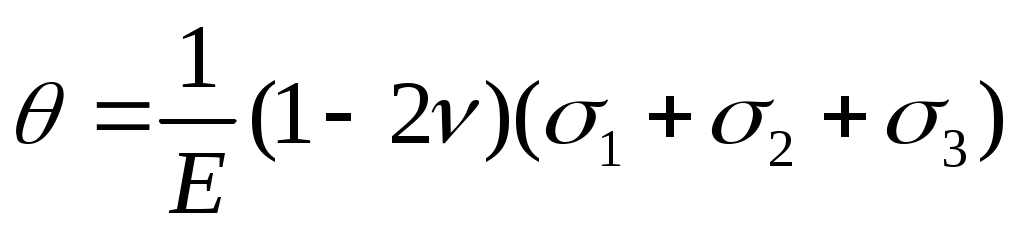 (4.25)
(4.25)
Рассмотрим случай всестороннего гидростатического сжатия материала, когда
1=2=3=-. По формуле (23) имеем
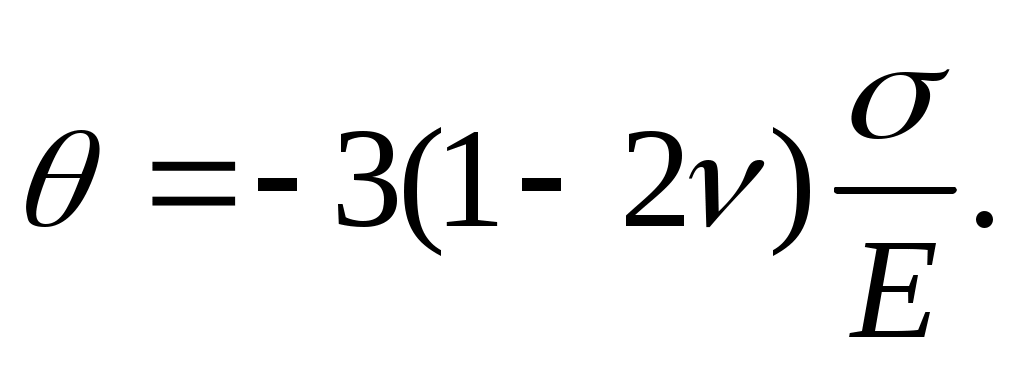
Из формулы видно, что коэффициент Пуассона не может быть больше 0,5, так как в противном случае при всестороннем сжатии тело увеличится в объёме.
При =0,5 материал деформируется без изменения объёма. В качестве примера подобного материала укажем на резину, для которой =0,47.
Удельная потенциальная энергия u при линейном растяжении равна
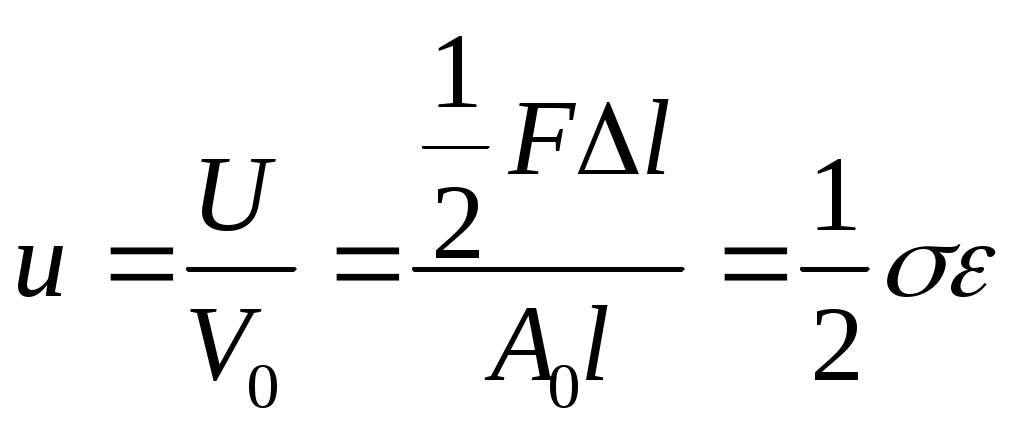
Обобщая полученную формулу на случай одновременного действия трёх напряжений, получим
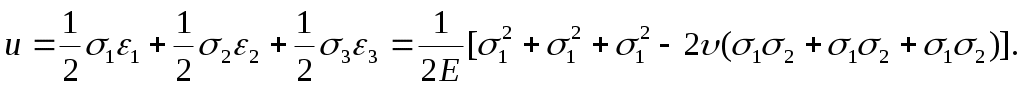 (4.26)
(4.26)
4.6 . Теории прочности
4.6.1. Задачи теории прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию. В зависимости от условии нагружения материал может находится в различных механических состояниях: упругом, пластическом и в состоянии разрушения.
Под предельным подразумевается такое напряженное состояние, при котором происходит качественное изменение свойств материала – переход от одного механического состояния к другому. Для пластических материалов предельным считается напряженное состояние, соответствующее заметным остаточным деформациям, а для хрупких – такое, при котором начинается разрушение материала.
Для простых напряженных состояний (растяжение, сжатие), оценка прочности может быть произведена сравнением расчетного напряжения с результатами опыта. За предельное значение в этом случае принимается предел текучести Т, для пластичных материалов и предел прочности В , для хрупких.
Таким образом, если известна расчетная величина напряжения , то коэффициент запаса по отношению к указанным пределам равны
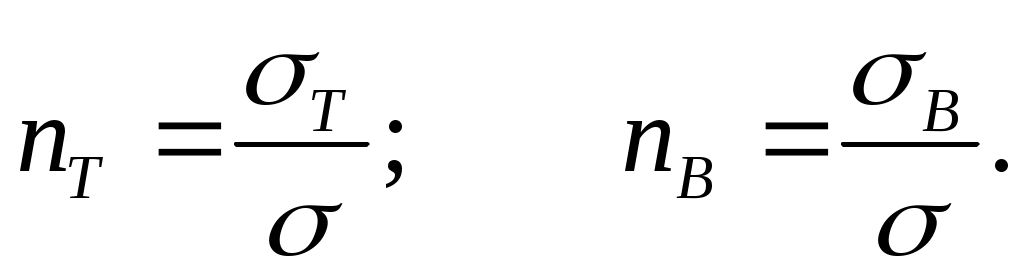 (4.27 )
(4.27 )
При плоском и объёмном напряженных состояниях для оценки прочности необходимо знать в каждой точке все три главных напряжения, для которых число встречающихся на практике соотношений по величине и знаку не ограничено. Поэтому число опытов, которые необходимо было бы провести, так велико, что практически неосуществимо.
Указанные обстоятельства приводят к необходимости создания такой методики расчёта, которая позволяла бы оценить степень опасности любого напряженного состояния для того или иного материала, основываясь главным образом на результатах опытов при простом растяжении и сжатии.
Считается, что на основе напряженного состояния и фактора определяющего разрушение материала, можно подобрать такой параметр, который характеризует степень нагружённости материала в условиях сложного напряженного состояния аналогично тому, что и при простом нагружении. Упомянутый параметр обычно имеет размерность напряжения и он называется эквивалентным напряжением экв или расч.
Определение истинной причины разрушения материала является труднейшей и в наше время до конца не разрешенной ещё задачей. Это обстоятельство не позволило создать единую теорию прочности.
4.6.2. Первая теория прочности основывается на том, что причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. Обычно эту теорию называют теорией наибольших нормальных напряжений.
В соответствии с принятой гипотезой должно соблюдаться следующее условие:
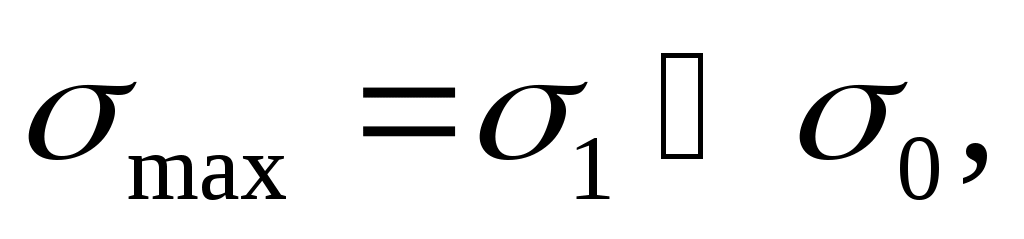 (4.28)
(4.28)
где 1 - величина набольшего из главных напряжений для исследуемого напряженного состояния;
0 – предельное напряжение, полученное из опыта на одноосное растяжение.
Условие прочности с коэффициентом запаса nимеет вид
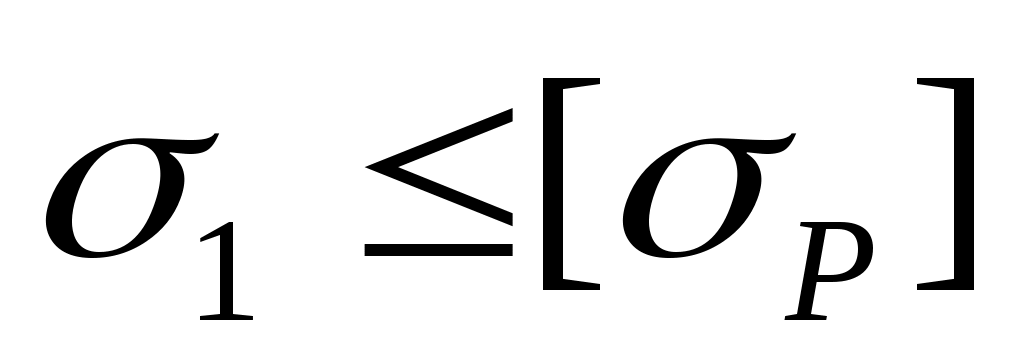 или
или 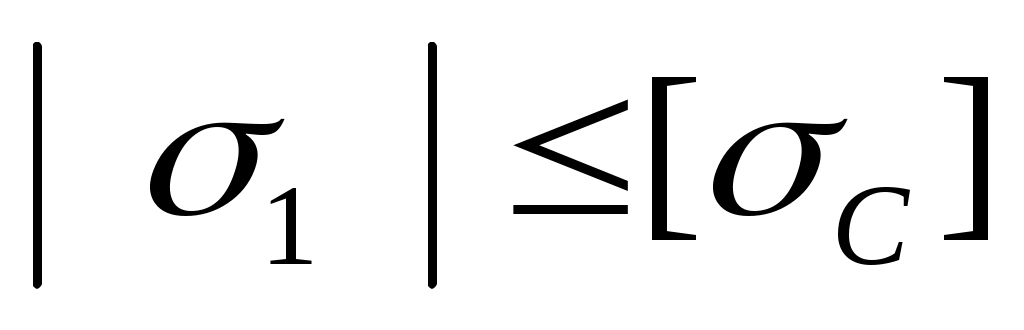 . (4.29)
. (4.29)
Главный недостаток теории наибольших нормальных напряжений состоит в том, что ею не учитывается два других главных напряжения: 2, 3.
Данная теория подтверждается опытом лишь при растяжении хрупких материалов.
4.6.3. Вторая теория прочности исходит из гипотезы о том, что причиной наступления предельного напряженного состояния в материале являются наибольшие удлинения. Эта теория получила название теории наибольших удлинений.
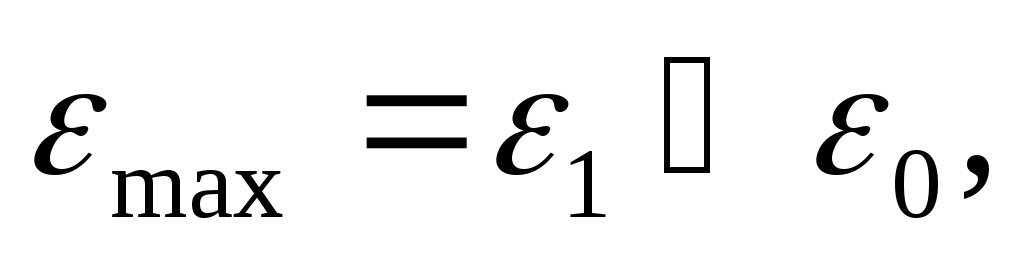 (4.30)
(4.30)
где 1 – расчетная величина наибольшего удлинения;
0– предельное значение относительного удлинения, полученное из опыта на одноосное растяжение.
При определении 1 и 0 используют закон Гука:
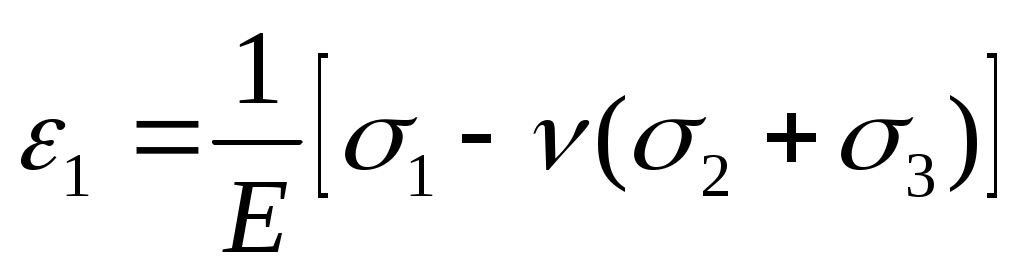
и
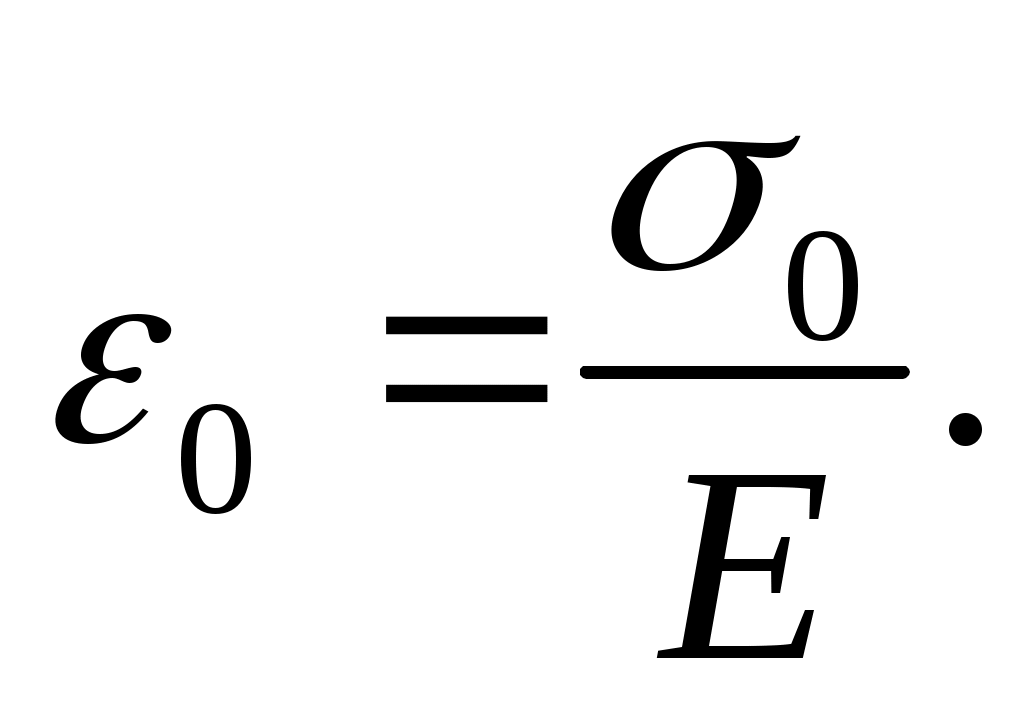
После подстановки
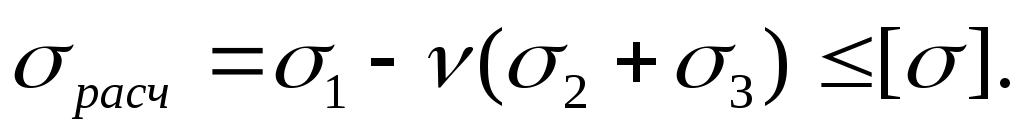 (4.31)
(4.31)
Это условие применяется лишь в тех случаях, когда расч. положительна.
Преимущество второй теории над первой состоит в том, чтоею учитываются влияние всех трех главных напряжений.
Как и первая, вторая теория недостаточно подтверждается опытами и большей степени оправдывается для хрупких материалов.
4.6.4. Третья теория прочности строится исходя из гипотезы, что причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения. Поэтому ей присвоено название теория наибольших касательных напряжений.
Так как экспериментально установлено, что пластические деформации сопровождаются сдвигами и соответствующим касательным напряжениям, то принятую гипотезу можно считать связанной с развитием заметных пластических деформации.
Используя равенства cos2 =0,5(1+ cos2); sin2 =0,5(1- cos2), формулу
(4.17) можно представить в следующем виде:
- 1 2 3 4 5 6 7 8 9 ... 21
Аналогия между зависимостями для напряженного и
деформированного состояний в точке
Найдем угол сдвига между двумя взаимно перпендикулярными отрезками АС и АВ (рис. 4.12,б), расположенными под угол к направлению главной
деформации 1
Отрезок АС в результате деформации повернулся на угол :
или
Для определения угла в формуле (а) угол надо заменить на
угол ( + 900).
Тогда получим
Так как прямой угол увеличился, то
Формулы (4.17) и (4.18) запишем вместе:
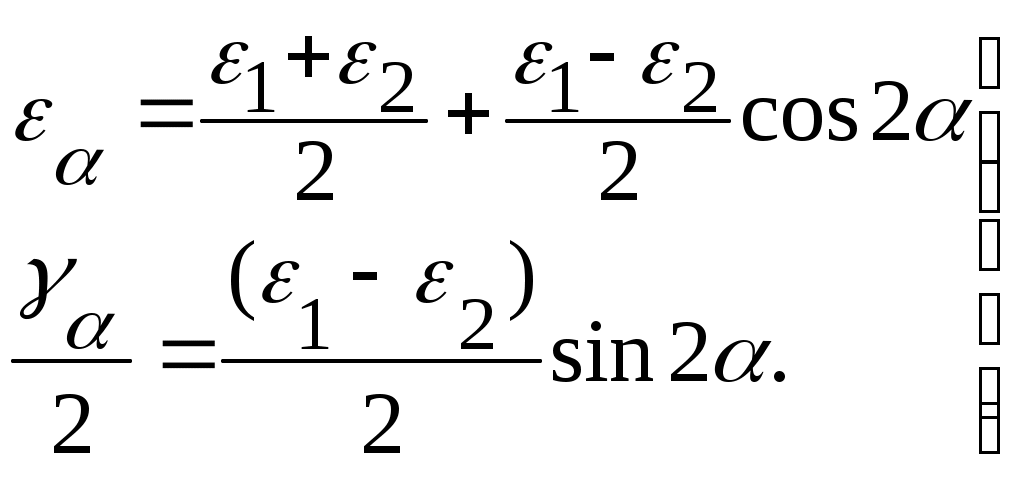 (4.19)
(4.19)Вспомним формулы (4.10) и (4.11), описывающие напряженное состояние в точке,
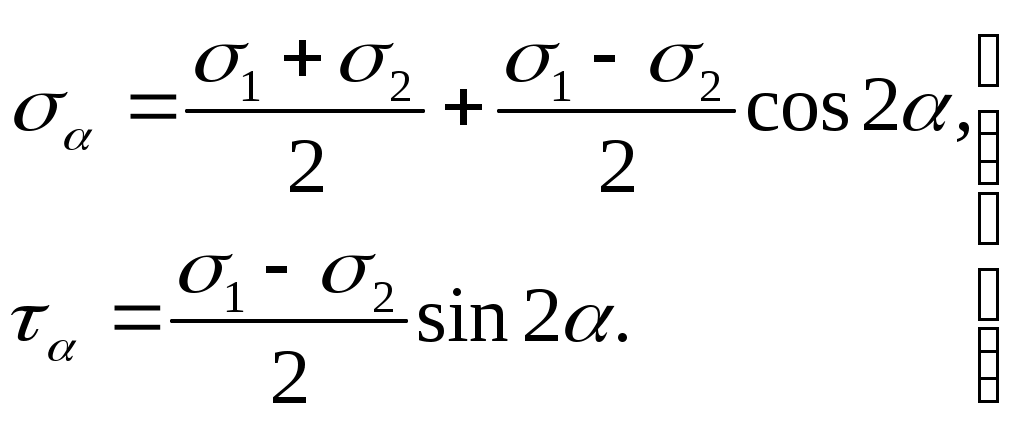 (4.20)
(4.20)Зависимости (4.19) и (4.20) указывают на математическую аналогию законов распределения , и деформаций и ( / 2) в точке.
На основании аналогии можно без вывода записать формулу
Из (4.21) следует, что
-
Обобщенный закон Гука для линейно упругого тела
Допустим, что элемент материала в виде кубика с ребрами единичной длины растягивается нормальным усилием 1 по направлению x (1 ) (рис. 4.13.)

Относительная деформация в направление этой оси
а в направлении осей y и zили 2 и 3
где Е - модуль продольной упругости; - коэффициент Пуассона.
По аналогии получим относительные деформации от растягивающих нормальных усилий 2 и 3 .
Следовательно,
Применяя подобное рассуждение к определению 2 и 3 , получим формулу обобщенного закона Гука:
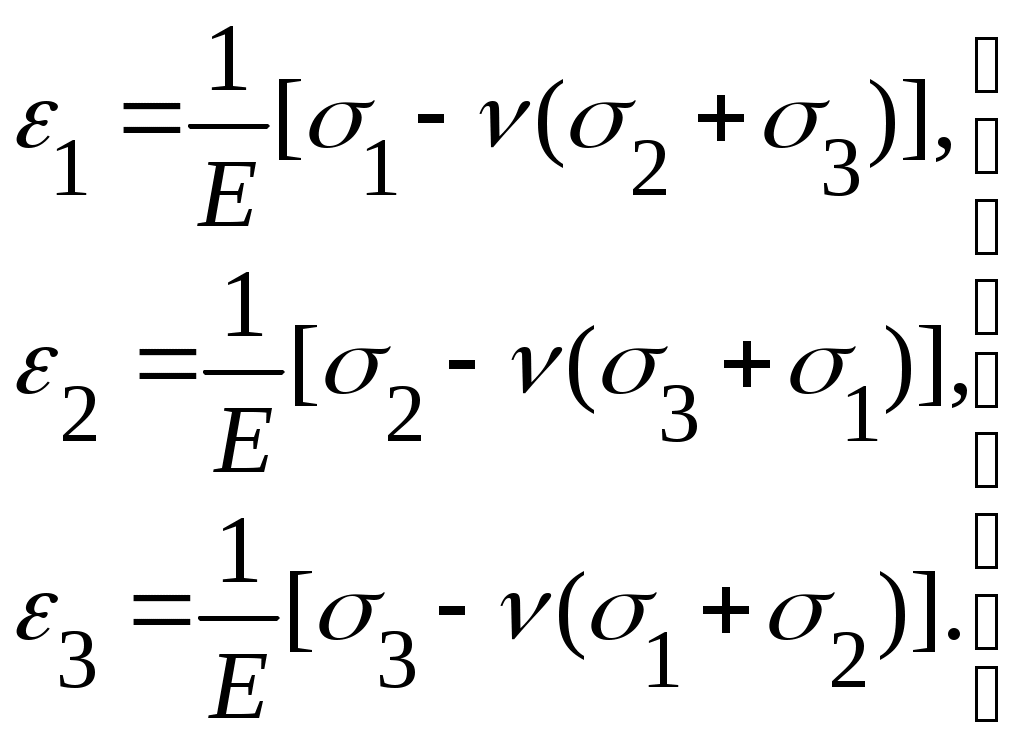 (4.23)
(4.23)-
Относительная объёмная деформация
Относительной объёмной деформацией называется отношение приращения объёма к его начальному значению
Пренебрегая произведением малых, запишем
Выражая деформации через напряжения согласно формулам (21), получим
Рассмотрим случай всестороннего гидростатического сжатия материала, когда
1=2=3=-. По формуле (23) имеем
Из формулы видно, что коэффициент Пуассона не может быть больше 0,5, так как в противном случае при всестороннем сжатии тело увеличится в объёме.
При =0,5 материал деформируется без изменения объёма. В качестве примера подобного материала укажем на резину, для которой =0,47.
-
Потенциальная энергия при объёмном напряженном состоянии
Удельная потенциальная энергия u при линейном растяжении равна
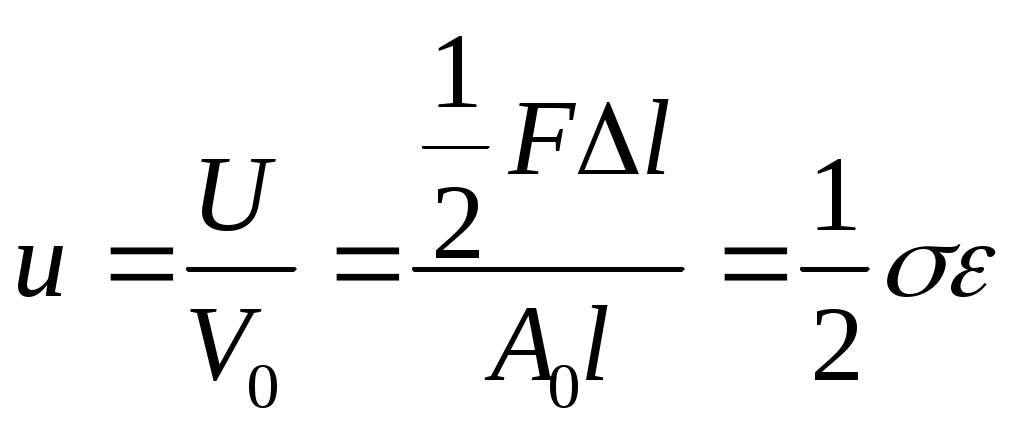
Обобщая полученную формулу на случай одновременного действия трёх напряжений, получим
4.6 . Теории прочности
4.6.1. Задачи теории прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию. В зависимости от условии нагружения материал может находится в различных механических состояниях: упругом, пластическом и в состоянии разрушения.
Под предельным подразумевается такое напряженное состояние, при котором происходит качественное изменение свойств материала – переход от одного механического состояния к другому. Для пластических материалов предельным считается напряженное состояние, соответствующее заметным остаточным деформациям, а для хрупких – такое, при котором начинается разрушение материала.
Для простых напряженных состояний (растяжение, сжатие), оценка прочности может быть произведена сравнением расчетного напряжения с результатами опыта. За предельное значение в этом случае принимается предел текучести Т, для пластичных материалов и предел прочности В , для хрупких.
Таким образом, если известна расчетная величина напряжения , то коэффициент запаса по отношению к указанным пределам равны
При плоском и объёмном напряженных состояниях для оценки прочности необходимо знать в каждой точке все три главных напряжения, для которых число встречающихся на практике соотношений по величине и знаку не ограничено. Поэтому число опытов, которые необходимо было бы провести, так велико, что практически неосуществимо.
Указанные обстоятельства приводят к необходимости создания такой методики расчёта, которая позволяла бы оценить степень опасности любого напряженного состояния для того или иного материала, основываясь главным образом на результатах опытов при простом растяжении и сжатии.
Считается, что на основе напряженного состояния и фактора определяющего разрушение материала, можно подобрать такой параметр, который характеризует степень нагружённости материала в условиях сложного напряженного состояния аналогично тому, что и при простом нагружении. Упомянутый параметр обычно имеет размерность напряжения и он называется эквивалентным напряжением экв или расч.
Определение истинной причины разрушения материала является труднейшей и в наше время до конца не разрешенной ещё задачей. Это обстоятельство не позволило создать единую теорию прочности.
4.6.2. Первая теория прочности основывается на том, что причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. Обычно эту теорию называют теорией наибольших нормальных напряжений.
В соответствии с принятой гипотезой должно соблюдаться следующее условие:
где 1 - величина набольшего из главных напряжений для исследуемого напряженного состояния;
0 – предельное напряжение, полученное из опыта на одноосное растяжение.
Условие прочности с коэффициентом запаса nимеет вид
Главный недостаток теории наибольших нормальных напряжений состоит в том, что ею не учитывается два других главных напряжения: 2, 3.
Данная теория подтверждается опытом лишь при растяжении хрупких материалов.
4.6.3. Вторая теория прочности исходит из гипотезы о том, что причиной наступления предельного напряженного состояния в материале являются наибольшие удлинения. Эта теория получила название теории наибольших удлинений.
где 1 – расчетная величина наибольшего удлинения;
0– предельное значение относительного удлинения, полученное из опыта на одноосное растяжение.
При определении 1 и 0 используют закон Гука:
и
После подстановки
Это условие применяется лишь в тех случаях, когда расч. положительна.
Преимущество второй теории над первой состоит в том, чтоею учитываются влияние всех трех главных напряжений.
Как и первая, вторая теория недостаточно подтверждается опытами и большей степени оправдывается для хрупких материалов.
4.6.4. Третья теория прочности строится исходя из гипотезы, что причиной наступления предельного напряженного состояния являются наибольшие касательные напряжения. Поэтому ей присвоено название теория наибольших касательных напряжений.
Так как экспериментально установлено, что пластические деформации сопровождаются сдвигами и соответствующим касательным напряжениям, то принятую гипотезу можно считать связанной с развитием заметных пластических деформации.