Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Полученный интеграл представляет собой статический момент площади поперечного сечения относительно нейтральной оси Ох, который равен нулю только в том случае, когда ось проходит через центр тяжести сечения. На основании этого можно сказать, что нейтральная ось при чистом изгибе прямого бруса проходит через центр тяжести сечения (точка С).

Подставив в формулу (7.1) вместо напряжения его значение по формуле (7.2), получим



Интеграл, входящий в это выражение, представляет собой осевой момент инерции поперечного сечения стержня



поэтому



откуда находим кривизну нейтрального слоя:

(7.4)

где величина EI_X называется жесткостью бруса при изгибе.

Подставляя это выражение в формулу (7.2), окончательно получим

(7.5)

Для прямоугольного сечения I_x=bh³/12, для круглого сечения I_x=d⁴/64.
Формула (7.5) позволяет определить напряжения в любой точке, лежащей на линии поперечного сечения бруса, отстоящей от нейтральной оси на расстоянии у. Из формулы видно, что напряжение зависит от величины у линейно (рис. 7.3). График, изображающий закон изменения напряжений по высоте сечения, называется эпюрой напряжений.

Формулу (7.5) можно использовать не только для сечения симметричного относительно оси Оу, но и для любого другого, при условии, что одна из главных осей инерции лежит в плоскости нагрузки.Для доказательства последнего утверждения приравняем нулю момент всех элементарных внутренних сил dA относительно

оси Оу.

Отсюда следует, что



Это значит, что оси хОу должны быть главными центральными осями сечения.

Для симметричного сечения это условие удовлетворяется автоматически, для остальных сечений плоскость нагрузки должна быть параллельна центральной оси.

---

Наибольшее напряжение будет в точке, которая наиболее удалена от нейтральной оси.



Отношение называется моментом сопротивления сечения при изгибе и обозначается W_X:

(7.6)

Для прямоугольного сечения W_x=bh²/6, для круглого сечения W_x=d³/320.1d³.
Таким образом

(7.7)

где - максимальный изгибающий момент;

Эта формула является основной при расчете на прочность бруса при изгибе.

0. 
   7.1.4. Касательные напряжения при изгибе
   

В отличие от чистого изгиба при поперечном изгибе в сечении бруса возникает не только изгибающий момент, но и поперечная сила. Поэтому в поперечном сечении наряду с нормальными напряжениями появляются также и касательные напряжения.

На основании закона парности касательных напряжений последние возникают также и в продольных сечениях и вызывают сдвиги отдельных волокон относительно друг друга.

Вследствие сдвигов гипотеза плоских сечений при поперечном изгибе нарушается, плоские до деформации сечения слегка искривляются (рис. 7.4.).



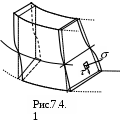
Т еоретические и экспериментальные исследования этого вопроса показали, что влияние этого эффекта на величину нормальных напряжений невелико и поэтому влиянием сдвигов на закон распределения нормальных напряжений пренебрегают.

Нормальные напряжения при поперечном изгибе определяют по формуле (7.5), применяемой при чистом изгибе:


Для вывода формулы касательных напряжений мысленно вырежем из балки (рис. 7.5,а) элемент длиной dzи дополнительным продольным сечением рассечем его на две части (рис. 7.5,б). Рассмотрим равновесие верхней части

---

, на которую с

ассмотрим равновесие верхней части, на которую с обоих торцов действуют сжимающие напряженияобоих торцов действуют сжимающие напряжения.


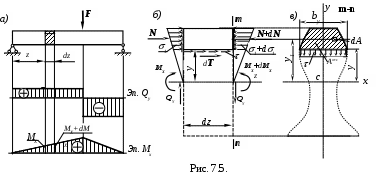
Так как изгибающий момент справа больше, чем слева, на величину dM_X, то



Сжимающая сила, действующая на отсеченную часть с правой стороны, больше, чем с левой, на величину
(а)

Интегрирование распространяется по площади отсеченной части А^ОТС, которая заштрихована на рис. 7.5, в.

Интеграл в выражении (а) представляет собой статический момент отсеченной части относительно нейтральной оси Сх.



Поэтому



Это усилие должно уравновешиваться касательными силами dT, возникающими в продольном сечении элемента (рис. 7.5,б). Примем, что касательные напряжения  распределены по ширине сечения b_y равномерно. Тогда

dT= dN,

или

,

откуда



Но



поэтому окончательно имеем

. (7.8)

Эту формулу называют формулой Журавского, по имени русского ученого Д.И. Журавского.

На основании закона парности касательных напряжений полученная формула определяет также напряжения и в поперечном сечении бруса.

Из формулы (7.8) видно, что касательные напряжения изменяются по высоте сечения по тому же закону, как и величина .

В прямоугольном сечении, у которого закон распределения касательных напряжений по высоте сечения такай же, как и для величины статического момента отсеченной части

---

.


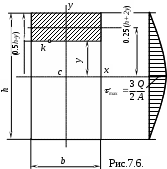Пример 1. П р я м о у г о л ь н о е с е ч е н и е. Рассмотрим распределение касательных напряжений в прямоугольном сечении. Возьмем произвольную точку k, отстоящую от нейтральной оси на расстоянии у (рис.7.6.). Проведем через эту точку прямую, параллельную нейтральной оси Сх.

Определим статический момент отсеченной (заштрихованной) части относительно нейтральной оси Сх.


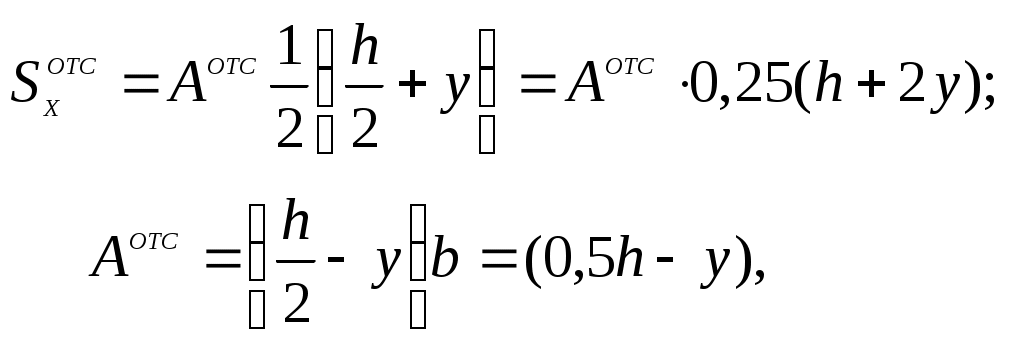
следовательно



Как известно,



Подставим в формулу (8) значения

Q, S, Iи b:

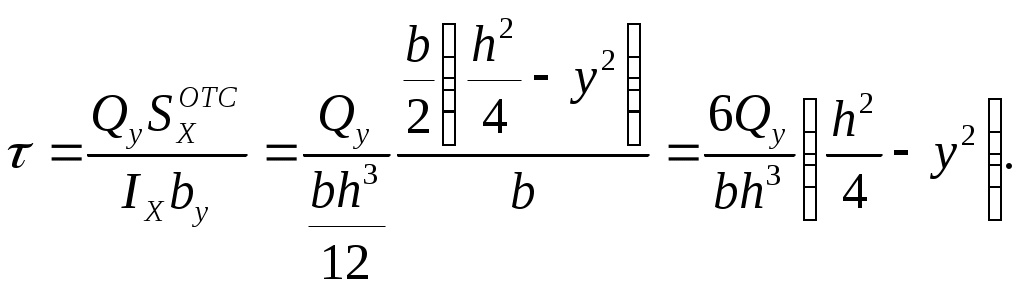(7.9)

Формула (7) показывает, что касательные напряжения по высоте сечения изменяются по закону квадратной параболы. При y=h/2 получим =0, а при у=0 имеем



На рис. 7.6. дан общий вид эпюры .
Пример 2. Д в у т а в р о в о е с е ч е н и е. Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки двутавра к его полке. В основном поперечную силу воспринимает стенка, а на долю полки приходится небольшая величина.

Рассмотрим произвольную точку k(рис. 7.7,a). Проведем через эту точку линию, параллельную оси Сх. Статический момент площади верхней отсеченной части может быть найден как сумма статических моментов площадей А₁ и А₂ :





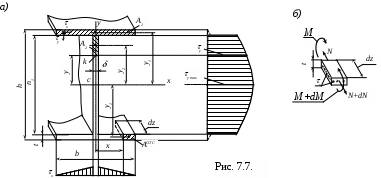
Эта формула справедлива, когда точка k находится в пределах вертикальной стенки, т.е. пока величина у лежит в пределах 0 у  (h₁/2).

Закон распределения касательных напряжений (_у ) в стенке определяется формулой (7.8) и показан на рисунке 7.7 справа отсечения. В полках эти напряжения невелики и практически не влияют на прочность балки то ими обычно не интересуются и потому их не вычисляют.

---

Значительно больший интерес в этой задаче представляют касательные напряжения (_х).

Картина распределения касательных напряжений здесь существенно меняется: они не только переменны вдоль ширины полки, но и направление их становится не параллельным, перпендикулярным Q_y.

Получим формулу для определения этих напряжений.

Вывод будет совершенно аналогичен выводу формулы (8). Выделим элемент полки длиной dz. Рассмотрим его в равновесии (рис. 7.7,а,б ).

Поскольку сейчас нас интересуют только касательные напряжения (_х), на рисунке (рис. 7.7,б ).не показаны. Предположим, что по толщине полки они распределены равномерно.

При таком допущении сдвигающая сила

dT=_хdzt. Растягивающая сила


По условию равновесия: dN=dT,

Поэтому окончательно имеем

(7.10)

На основании закона парности касательных напряжений полученная формула определяет также напряжения по ширине полки в направлении оси Сх.

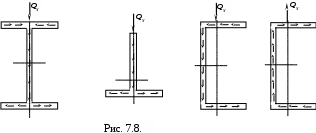
Напряжения _хвсегда образуют единый поток с касательными напряжениями _у в стенке профиля (рис. 7.8). Последние же определяются по формуле Журавского и направлены в сторону Q_Y.

Формулы (7.8) и (7.10) дают возможность вычислить касательные напряжения в любой точке тонкостенного профиля и построить полную эпюру касательных напряжений.

5. 1   ...   4   5   6   7   8   9   10   11   ...   21

---