Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 404
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
Рассмотрим такие балки, у которых поперечное сечение имеет ось симметрии, а все силы, действующие на балку, лежат в плоскости, совпадающей с этой осью.
На рис. 8.1, а показана изогнутая балка. В результате изгиба ось балки становится криволинейной.
П
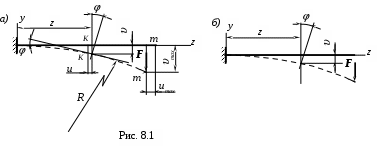
еремещения центра тяжести сечения по направлению у, перпендикулярному оси балки, называется прогибом балки в данной точке (сечении) и обозначается .
Нетрудно видеть (рис. 8.1), что прогиб является переменным по длине, т.е. имеем
Угол , на который сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения. Учитывая, что повернувшееся сечение перпендикулярно изогнутой оси балки, заключаем, что вместо определения угла поворота сечения можно определять равный ему угол между касательной к данной точке изогнутой оси и первоначальной осью балки (рис. 8.1, а), где прогиб - и угол поворота сечения - даны для точки К. Перемещения центра тяжести сечения по направлению z обозначают через u.
Три величины- ,u и -являются компонентами перемещения произвольного сечения балки.
Проверка жесткости балки сводится к требованию, по которому наибольший прогиб maxне должен превышать определенной доли пролета:
max =l /m.
Число m устанавливается нормами проектирования примерно в пределах от 300 до 1000.
Это позволяет при малых прогибах :
во- первых, угол наклона касательной к оси изогнутой балки определять с помощью выражения
во – вторых, перемещениями u можно пренебречь, так как по сравнению с они будут величинами второго порядка малости.
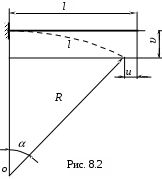
В самом деле, рассмотрим, например, балку длиной l, заделанную одним концом (рис. 8.2). Предположим, что она изогнулась по окружности. Вертикальное и горизонтальное перемещение свободного конца равны:
где
- угол поворота концевого сечения.
Р
 азложим cosи sinв ряд и ограничимся ввиду малости двумя членами ряда:
азложим cosи sinв ряд и ограничимся ввиду малости двумя членами ряда: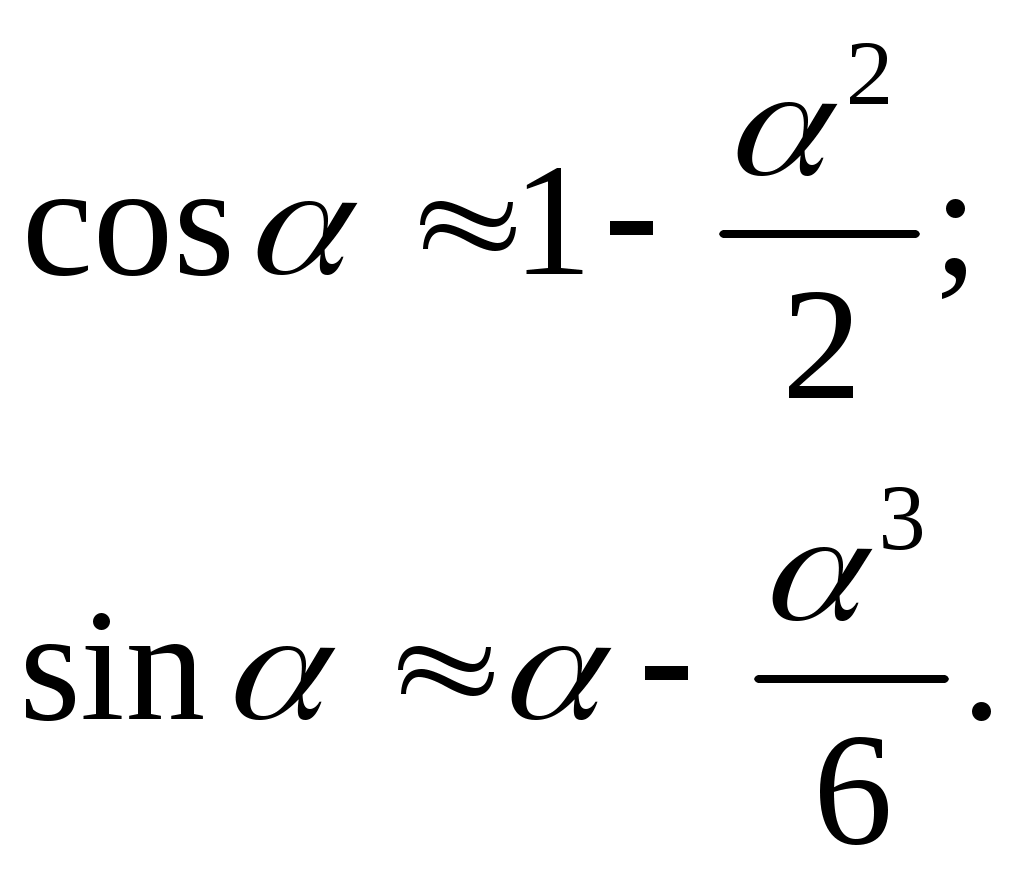
После подстановки получим:
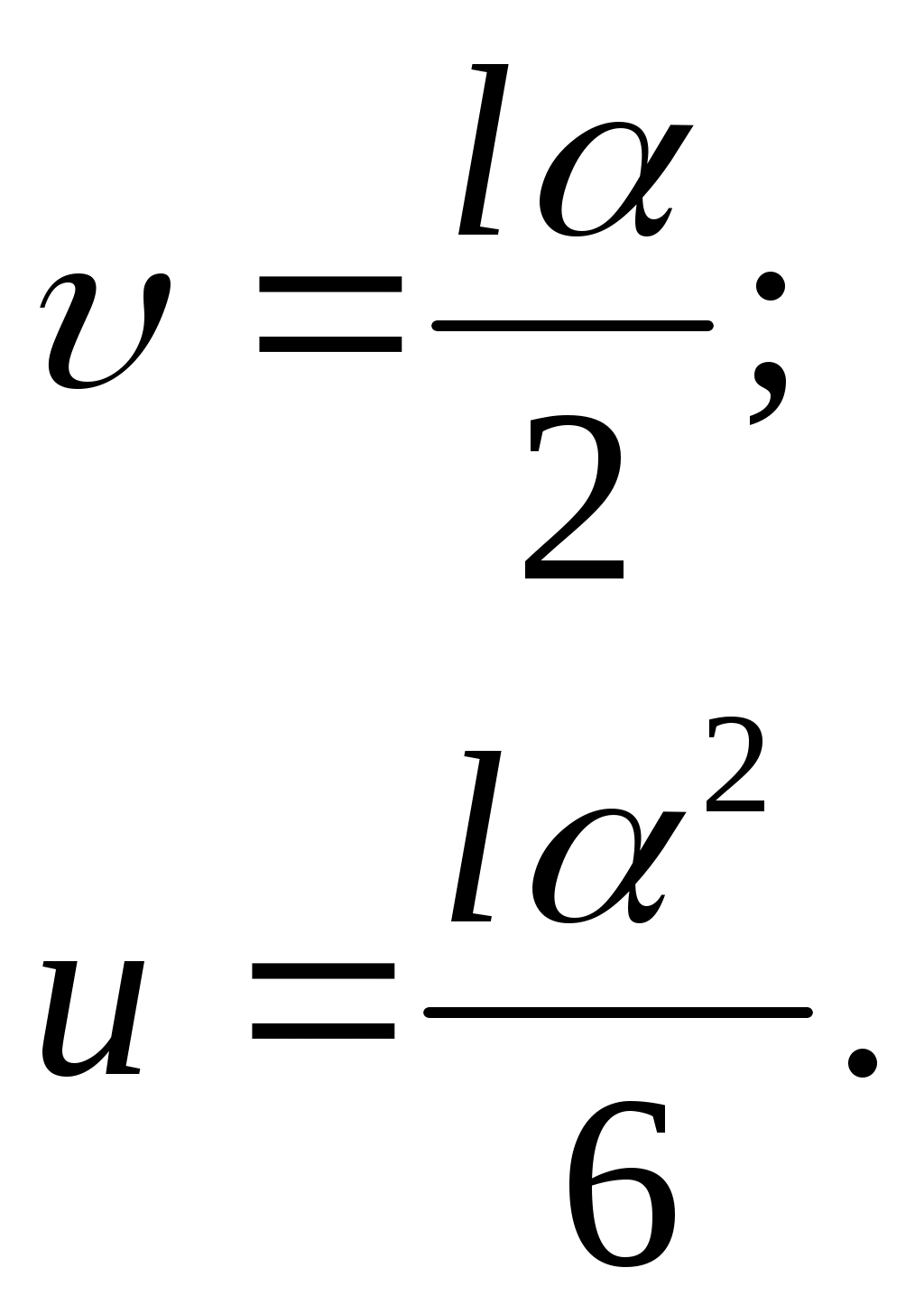
Отсюда следует,
что и - величины одного порядка, а uимеет более высокий порядок малости. Например, =l/100, тогда=1/50, аu=l/15000, т.е. горизонтальное перемещение в 150 раз меньше, чем вертикальное. Разница между uи в реальных конструкциях ещё больше.
На рис. 8.1,б показана условная схема перемещений. Считается, что каждая точка перемещается только по вертикали.
Для определения полной картины деформаций необходимо получить уравнение оси изогнутого бруса
Если функция
8.2. Дифференциальные уравнения оси изогнутого бруса
Ранее была получена связь между кривизной и изгибающим моментом при чистом изгибе
Это соотношение выполняется также и при поперечном изгибе.
Из курса высшей математики известно, что
Исключая из (8.3) и (8.4) кривизну, получаем дифференциальное уравнение изогнутой оси стержня
Интегрирование этого нелинейного дифференциального уравнения связано с большими трудностями. Учитывая, что на практике приходится иметь дело с малыми прогибами, и, что тангенсы углов наклона малы, квадратом первой производной в знаменателе по сравнению с единицей можно пренебречь. Тогда получим приближенное дифференциальное уравнение
Два знака в уравнении (6) поставлены потому, что знак кривизны может не совпадать со знаком изгибающего момента. Знак кривизны зависит от направления осей координат. Знак изгибающего момента зависит от того, где расположены растянутые волокна (рис. 8.3,а,б). Таким образом, когда ось Оу (рис. 8.3,а) направлена вверх, знаки кривизны и изгибающего момента совпадают, поэтому в дифференциальном уравнении берется з
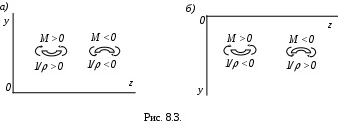
нак плюс:
Если знаки у кривизны и изгибающего момента различны (рис. 8.3,б), то берется знак минус:
Уравнение (8.6) является обыкновенным дифференциальным уравнением второго порядка, которое интегрируется способом разделения переменных.
Запишем его, удерживая знак «+» в виде
или
Интегрируем левую и правую части уравнения независимо. Получаем
или
Далее
Или

Величины С и D – это постоянные интегрирования, которые чаще всего определяются из условий закрепления балки. Размерности: [C]=Нм2, [D]= Нм3.
Пример 1. Составить выражение прогиба и угла поворота в произвольном сечении консольной балки AB, загруженной силой F (рис. 8.4.).
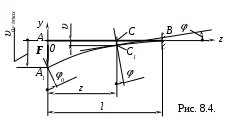 Имеем
Имеем
Двукратное интегрирование дает
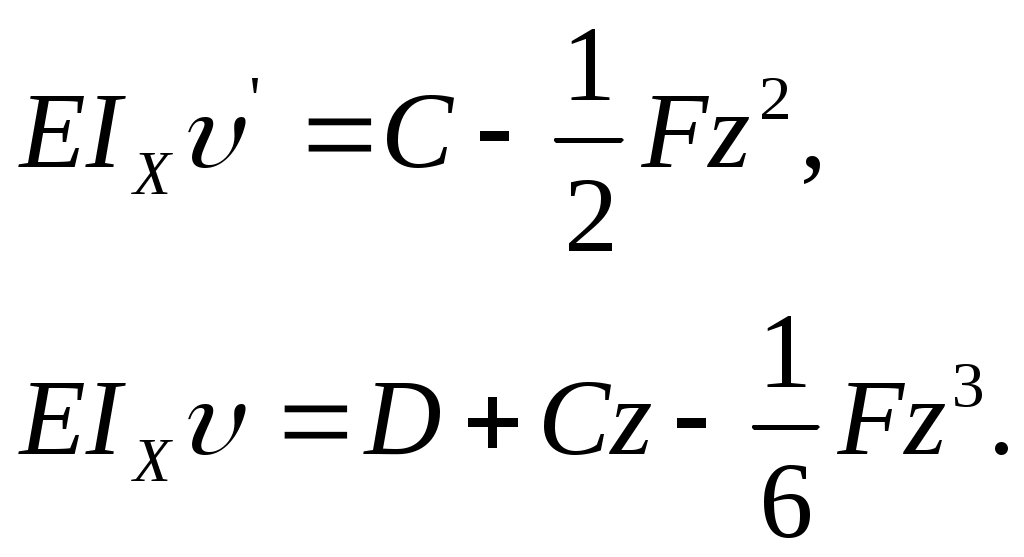
Постоянные С и D определим из условий закрепления: в заделке (при z=l) угол поворота и прогиб равны нулю. Другими словами, имеем
что позволяет записать
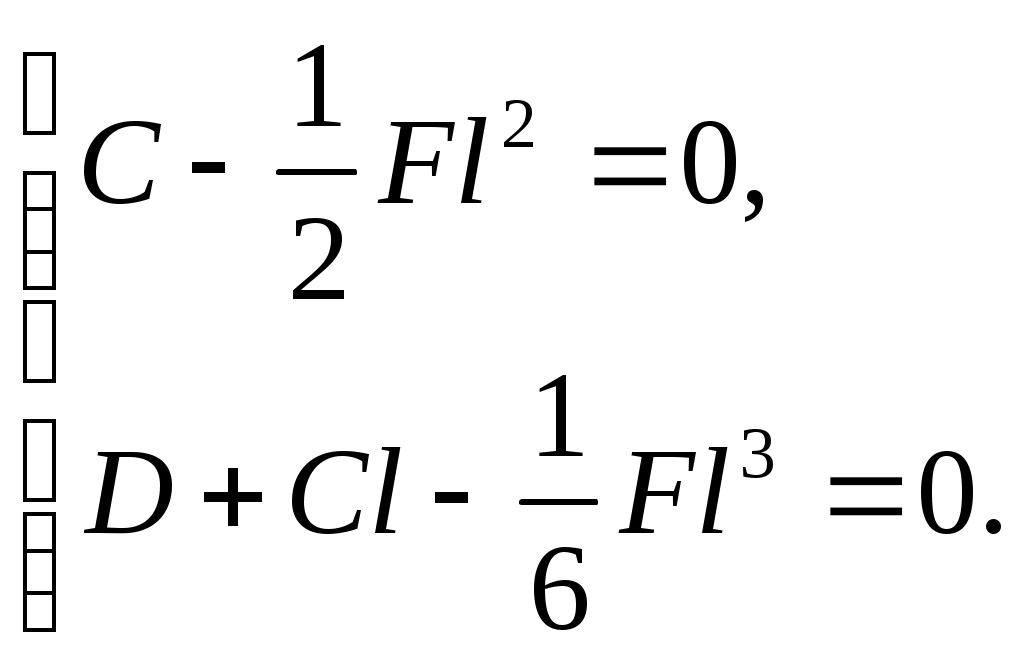
Из решения этой системы уравнений получаем
С учётом найденных постоянных можно записать уравнения углов поворота и прогибов
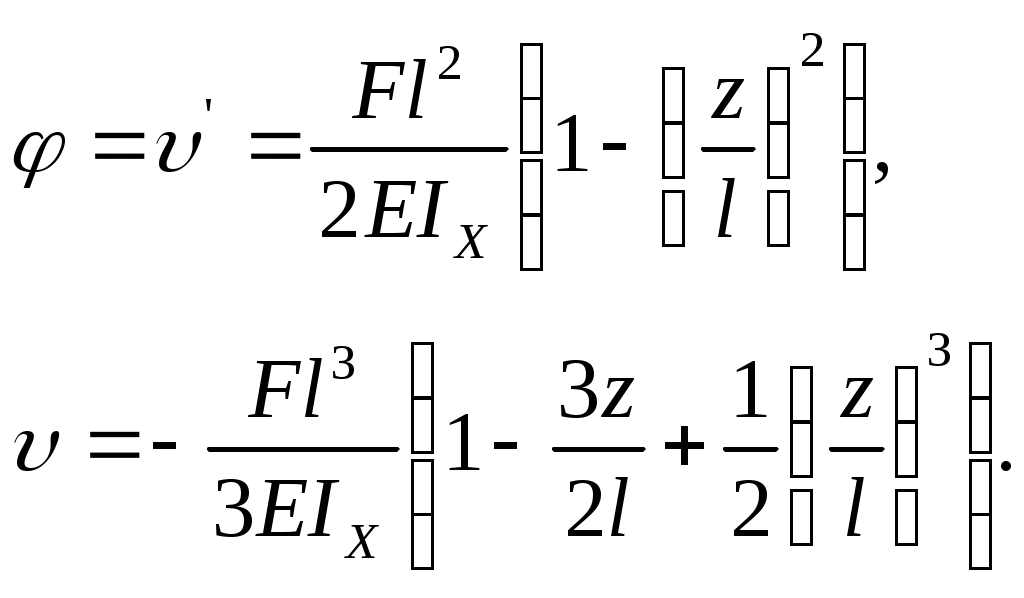
В частности, для концевого сечения получается
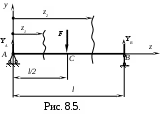
Пример 2. Для балки, нагруженной по схеме (рис. 8.5), нельзя записать единого выражения изгибающего момента. В данном случае для каждого участка необходимо составить выражение изгибающего момента: М1= М1(z) и М2= М2(z) для участков АС и СВ соответственно. Поэтому дифференциальных уравнений изогнутой оси балки будет также два. Интегрируя каждое из этих уравнение, получим четыре постоянных интегрирования ( по две на каждом участке).
 С целью снижения трудоёмкости решения подобного рода задач применяют метод составления дифференциальных уравнений, когда оказывается что С1= С2= С3= С4 = … = Сn= С и D1= D2= … = Dn= D.
С целью снижения трудоёмкости решения подобного рода задач применяют метод составления дифференциальных уравнений, когда оказывается что С1= С2= С3= С4 = … = Сn= С и D1= D2= … = Dn= D.Этот метод формулируется так:
1. Начало координат для всех участков следует брать в одной и той же точке на одном из концов балки.
2. При составлении выражений изгибающих моментов следует рассматривать всегда ту часть балки, которая содержит начало координат. Тогда выражение изгибающего момента рассматриваемого участка будет содержать слагаемые, входящие в выражения изгибающих моментов предыдущих участков.
3. Интегрирование дифференциальных уравнений должно проводиться без раскрытия скобок.
Для балки, нагруженной по схеме (рис. 8.5):IX=I.
Первый участок
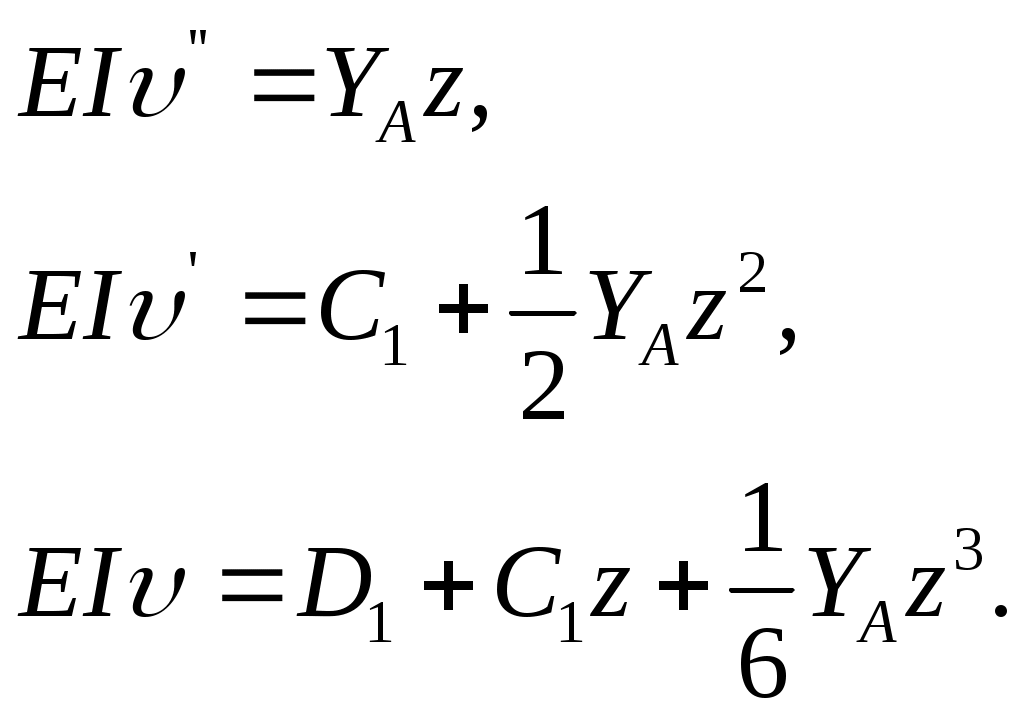
Второй участок
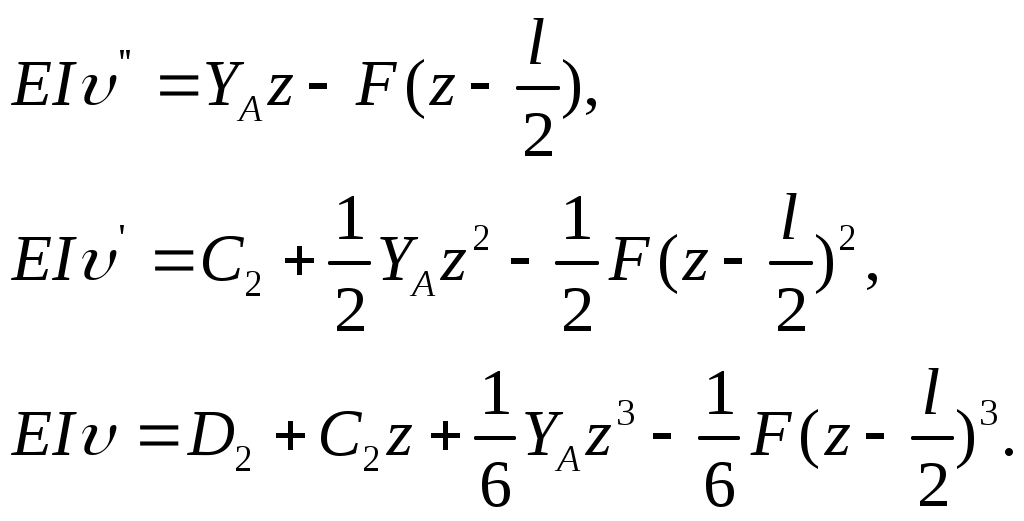
На стыке первого и второго участков изогнутая ось бруса не терпит разрывов и угол поворота сечения один и тот же, т.е. имеет место
или
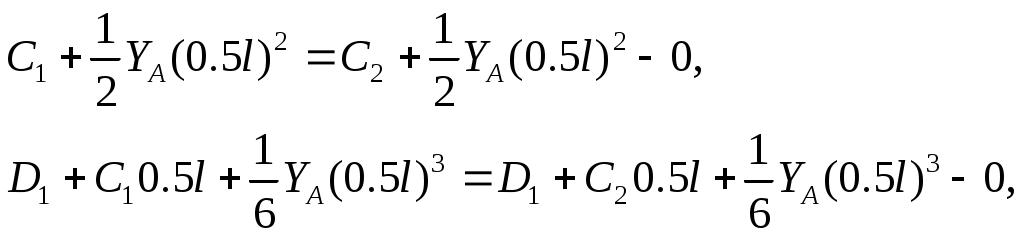
откуда следует
Постоянные интегрирования С и D найдутся из условий закрепления:
Получим:
-
3. Метод начальных параметров
Задача определения прогибов может быть значительно упрощена, если применять так называемое универсальное уравнение оси