Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 386

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Деформация, остающаяся в теле после разгрузки, получила названиеостаточной или пластичной, а способность тела приобретать пластическую деформацию – пластичность.

Сплошность

7.1.1. Общие замечания

Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу

Методика расчёта

Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической(Fкр ). Таким образом, исследование устойчивости стержня заключается в определении Fкр. Для обеспечения устойчивости допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки Fкр к её допускаемой величине ([F]y) называется коэффициентом устойчивости: (11.1)Коэффициент ny зависит от материала стержня. Его рекомендуемые величины находятся в пределах: для стальных стоек 1.5…3; для деревянных 2.5…3.5; для чугунных 4.5…5.5. Метод Эйлера для определения критической силы. Формула Эйлера.Для исследования устойчивости равновесия упругих систем имеется несколько методов: метод малых колебаний, энергетический метод и др. В инженерной практике для невесомых стержней с нагрузкой, приложенной точно в центре тяжести торцовых сечений и параллельно продольной оси стержня используют более простой метод – метод Эйлера.Метод Эйлера основан на анализе разветвления форм равновесия упругой системы. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. Для вывода формулы Эйлера рассмотрим шарнирно - опёртый, центрально - сжатый стержень постоянного сечения (рис. 11. 3) в слегка отклонённом состоянии от прямолинейной формы.Изгибающий момент в произвольном сечении равенF (11.2)Дифференциальное уравнение изгиба стержня запишется в виде: (11.3)или (11.4)где (11.5)Интеграл дифференциального уравнения (11.4) имеет вид (11.6)Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z=0 и Следовательно, уравнение оси изогнутого бруса (6) примет вид (11.7)Таким образом, стержень изгибается по синусоиде.Второе граничное условие: при z=l и  Bsinkl=0Это условие выполняется в двух случаях:1) В=0; 2) sinkl=0Первый случай нас не интересует, так как при В=0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.Второе условие sinkl=0 дает kl= 2 3 nучтя значение k (11.5), получим: Итак, получено не одно, а множество значений критической силы. Каждой критической силе соответствует своя форма равновесия (рис. 11.4). Подставляя найденное значение k в уравнение оси изогнутого бруса (11.7), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы. Равновесие, соответствующее первой форме изгиба, является устойчивым, а все всем остальным – неустойчивым.Для инженерных расчетов практический интерес представляет только наименьшая критическая сила (11.8)Эту формулу в 1744 г. впервые получил Леонард Эйлер, поэтому она называется формулой Эйлера, а определяемую этой формулой критическую силу – эйлеровой силой.Из формулы (11.8) видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.Таким образом, выясняется резкая разница между работой стержня на растяжение и на сжатие. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и поэтому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина. Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких- либо заметных признаков потери устойчивости, как правило, установить не удается.11.3. Влияние способов закрепления концов стержня на величинукритической силыНа рис. 11.5 показаны различные случаи закрепления концов сжатого стержня. Для каждого случая необходимо проводить свое решение аналогичное тому, что сделано в предыдущем параграфе для шарнирно опертого стержня. Эти решения показывают, что для всех случаев, изображенных на рис. 11.5, критическую силу можно представить в виде формулы: (11.9)где   коэффициент приведения длины, а величина ll0называется приведенной (свободной) длиной. Понятие о приведенной длине было впервые введено профессором Петербургского института путей сообщения Ф.С. Ясинским (1892).Свободная длина l0может быть истолкована как некоторая условная длина шарнирно опертого стержня, имеющего такую же критическую силу, как заданный стержень. В отдельных случаях это положение вытекает из чисто геометрического толкования (длина полуволны синусоды). Так, например, если стержень заделан одним концом, рассматривать как половину стержня, шарнирно опертого по концам, то l0= 2l. Следовательно, =2.Для стержня, заделанного двумя концами, длина полуволны, замеренная между двумя точками перегиба, где Мх=0,составит половину длины стержня, следовательно, для этого случая =0,5. 11.4. Пределы применимости формулы Эйлера. Формула Ясинского Формула Эйлера, полученная более 267 лет назад, долгое время являлась предметом дискуссий. Формула Эйлера для некоторых случаев не подтверждалась экспериментами. Объясняется это тем, что формула Эйлера выводилась в предположении, что при любом значении силы стержень работает в пределах упругих деформаций с использованием закона Гука. По этому формулу Эйлера нельзя применять в случаях, когда критические напряжения больше предела пропорциональности. Для установления предела применимости формулы Эйлера найдем Здесь радиус инерции. Обозначим через  Величина  называется гибкостью стержня.Итак, (11.10) Это так же формула Эйлера, но записанная для критического напряжения, а не для критической силы. Принято изображать уравнение (11.10) в координатах кр -(рис. 11.6). Полученную кривую часто называют гиперболой Эйлера. Как видно из уравнения (11.10), при малых гибкостях критические напряжения могут значительно превосходить предел прочности материала. Действительно короткие и толстые стержни (например, кубы, имеющие гибкость 

Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.

Так как

Отсюда определяется меридиональное напряжение т.

Напряженное состояние является двухосным

Из формулы Лапласа находим

где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки

15. Динамическое действие нагрузок

15. Динамическое действие нагрузок…………………………………..216


Анализ напряженного состояния при изгибе


В произвольной точке (т. К) поперечного сечения балки нормальные и касательныенапряжения определяются по формулам (7.5) и (7.8). Элемент, выделенный около этой точки, испытывает плоское напряженное состояние вида, указанного на

рисунке 7.9,а,б.



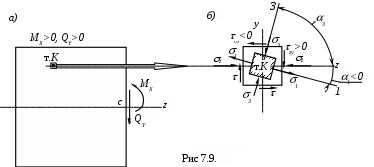
В нашем случае, если предположить, что отдельные волокна не давят друг на друга, и тогда у=0; z =; а на основании закона парности касательных напряжений zy=yz=, тоформула для главных напряжений примет вид:


Направление главных напряжений определяется углами 1 и 3, образуемые с продольной осью балки (осью z), которые находятся по формуле:


Проверка по формулам:






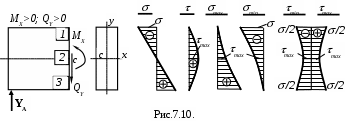
Исследуем напряжения в трех точках, лежащих в одном и том же поперечном сечении, но взятых на разной высоте (рис. 7.10.), а именно: в верхнем сжатом волокне (точка 1), в нейтральном слое (точка 2) и в нижнем растянутом волокне (точка 3).

В точке 1: =0;



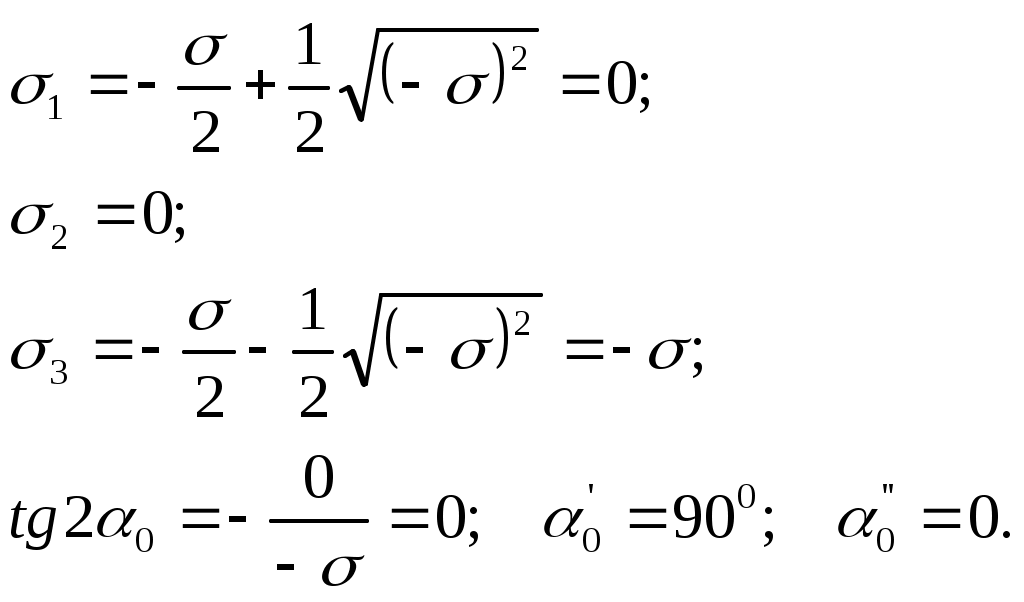
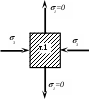
В точке 2:




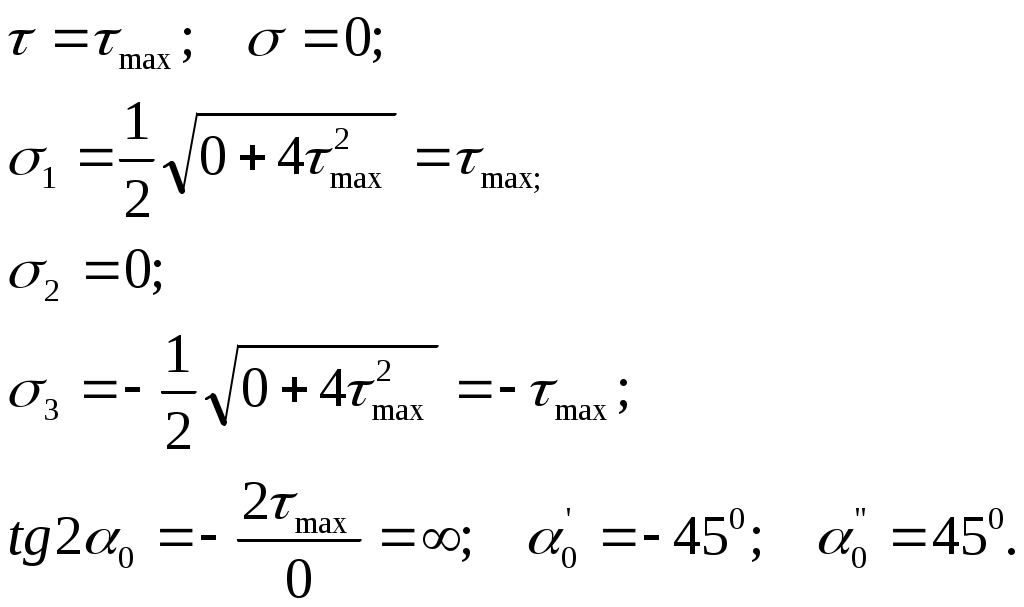
В точке 3: =0;




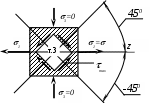
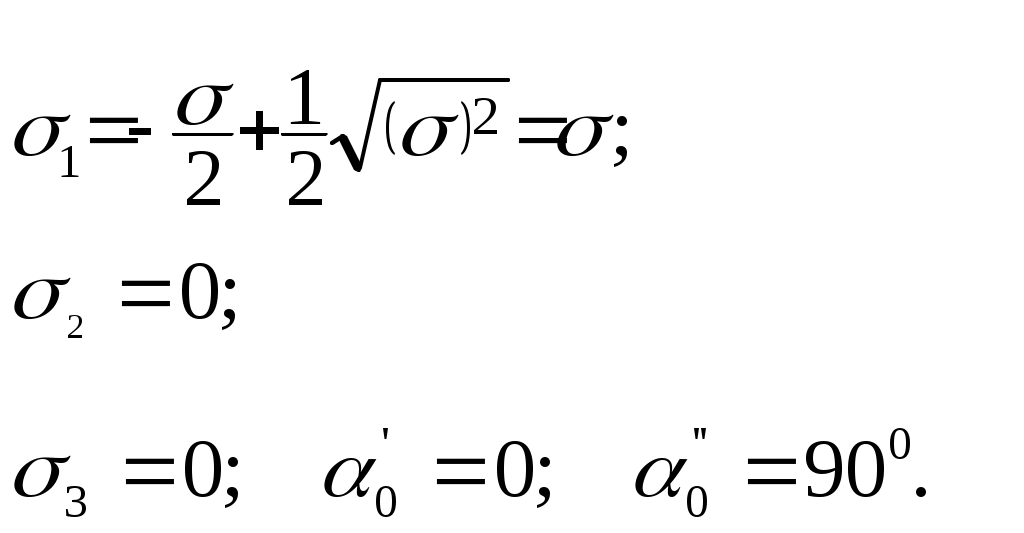
Наибольшие касательные напряжения равны



и которые развиваются в площадках, наклоненных к главным площадкам под углом 45
0, например, для точки 3.
Вычисляя главные напряжения для целого ряда точек сечения, можно построить эпюры (рис. 7.10.) главных растягивающих, главных сжимающих, а также наибольших касательных напряжений, которые развиваются в площадках, наклоненных к главным площадкам под углом 450.

Интересно отметить, что на нейтральной оси численные значения ординат всех эпюр, кроме первой, одно и то же.

Для наглядности потока распределения главных напряжений строят траектории главных напряжений. Так называется линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке.


По траекториям 1 можно судить о том, где и каком направлении могут появиться трещины, если материал балки плохо работает на растяжение. При армировании железобетонных балок арматуру целесообразно располагать в зонах и по возможности по направлению растягивающих напряжений.

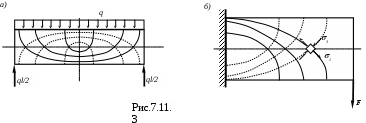
Траекторииглавных напряжений зависят от типа нагрузки и способов закрепления балки (рис. 7.11.).

Для выявления траекторииглавных напряжений часто используют метод лаковых покрытий. Метод лаковых покрытий обычно применяют для выявления общего распределения деформаций и напряжений, а также для определения наиболее нагруженных зон на поверхности детали. В хрупком лаковом покрытии трещины образуются в направлении, перпендикулярном главным растягивающим напряжениям 1, поэтому они совпадают с траекториями главных сжимающих напряжений 3.

(рис. 7.11. a,б).


      1. Подбор сечений и проверка прочности при изгибе


Условие прочности должно быть записано для так называемой опасной точки балки. Опасной точкой будет одна из трех точек (рис. 7.10.): а) точка, где нормальные напряжения достигают набольшей величины; б) точка, где касательное напряжение достигает наибольшей величины; в) точка, где и , хотя и не принимают наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание, т.е. создают наибольшее приведенное напряжение по принятой для расчета теории прочности.

Первая точка (рис. 7.10.) будет расположена в крайних волокнах того сечения, в котором изгибающий момент достигает максимальной величины.


В соответствии с формулой (7) условие прочности примет вид

(7.11)

где - максимальный изгибающий момент;

- момент сопротивления сечения относительно нейтральной оси.

Из условия прочности (7.11) при данном изгибающем моменте определяется требуемый момент сопротивления

(7.12)

по которому назначаются поперечные размеры балки.

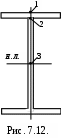Точка 2 (рис. 7.10.) находиться на нейтральной линии сечения, где от поперечной силы касательные напряжения имеют наибольшее значение, а нормальных нет. В этой точке будет чистый сдвиг, и условие прочности будет иметь вид

(7.13)

Прочность по главным напряжениям проверяют в зависимости принятой теории прочности по одной из формул:

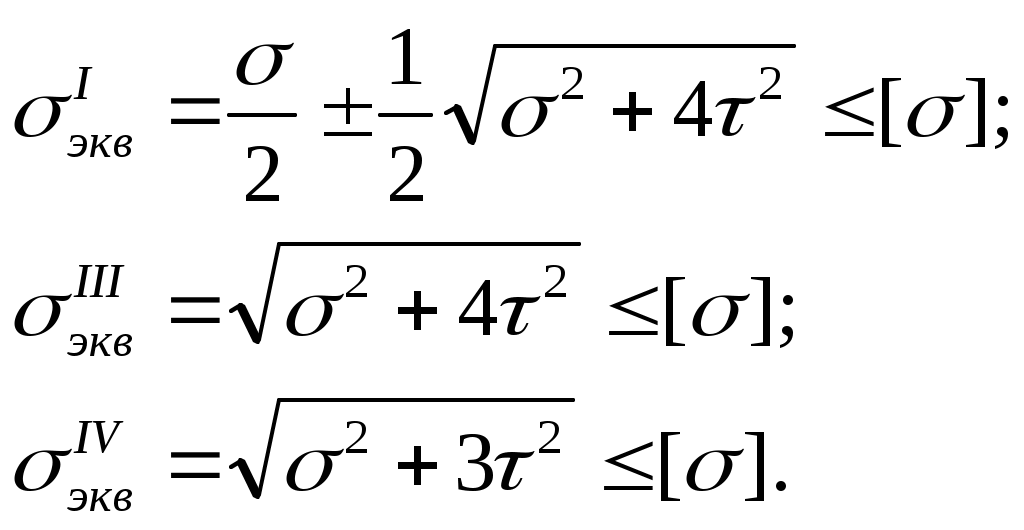(7.14)

Для уточнения отдельных размеров производится проверка прочности в отдельных точках.

Например, для балок двутаврового сечения (рис. 7.12.) такая проверка проводится в точке 1 по формуле (7.11); в точке 2 – по эквивалентным напряжениям, формула (7.14); в точке 3 – по касательным напряжениям, формула (7.13).

Размеры поперечных сечений сложной формы определяют путём попыток.

Следует стремиться к тому, чтобы подобранное сечение было возможно более рациональным по расходу материала, т.е. таким сечением, для которого отношение Wх/Aимеет возможно большее значение. Для этого следует возможно большую часть площади поперечного сечения располагать как можно дальше от нейтральной оси.

На рис. 7.13. показаны пять поперечных сечений балки, имеющих одинаковые площади; каждое сечение состоит из одного листа и четырех неравнобоких уголков . Наиболее рациональным из них является то, у которого момент сопротивления Wх больше, т.е. у которого больше момент инерции Ix (рис. 7.13,д). Сечения на рисунке расположены в порядке возрастания их моментов инерции, моментов сопротивления и, следовательно в порядке возрастания прочности балок.





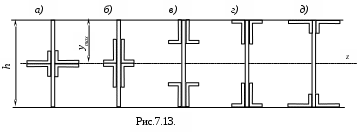
Для несимметричных сечений (см. рис 7.14.) формулой (7.7) можно пользоваться только для определения самых больших по модулю напряжений, т.е. для крайнего волокна сечения, которое наиболее удалено от нейтральной оси.

Тогда

(7.15)


Если же материал (чугун, бетон) не одинаково работает на растяжение и сжатие, то необходимо провести два расчета на прочность по величинам [р] и [с].

(7.16)

где и .


      1. Балки равного сопротивления изгибу

Подбор сечений производят по более напряженному сечению, в котором изгибающий момент достигает наибольшей величины. В остальных местах, где изгибающие моменты меньше, размеры поперечных сечений можно было бы уменьшить. Возникает задача о выборе рационального закона изменения сечения по длине балки. Если нормальные напряжения во всех поперечных сечениях равны допускаемому напряжению, то получим так называемую балку равного сопротивления изгибу.

На рис 7.15. показана балка с прямоугольным поперечным сечением, у которой высота постоянна, а ширина меняется по линейному закону:

h(z)=h=const, b(z)=(b0 /l).z.

Момент сопротивления сечения на расстоянии zот силы Fравен



где W0X – момент сопротивления в заделке.





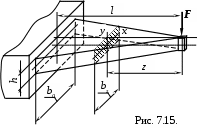
Изгибающий момент в том же сечении равен

MX(z)=Fz.

Напряжения в наиболее удаленном волокне данного сечения определяются по формуле



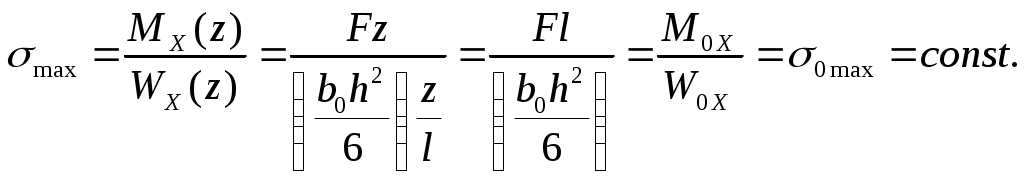
З
десь М0Х – момент в заделке;


max – напряжение в крайнем волокне сечения у места заделки.

Таким образом, наибольшие нормальные напряжения во всех сечениях бруса одинаковы, следовательно, получили балку равного сопротивления изгибу.

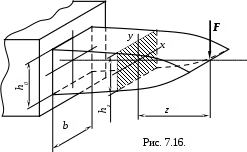
Рассмотрим ещё один пример балки равного сопротивления изгибу, у которой ширина постоянная, а высота переменная (рис. 7.16.).
Определим закон изменения высоты из условия равной прочности, т.е. из условия постоянства наибольших напряжений (расч =[] ):



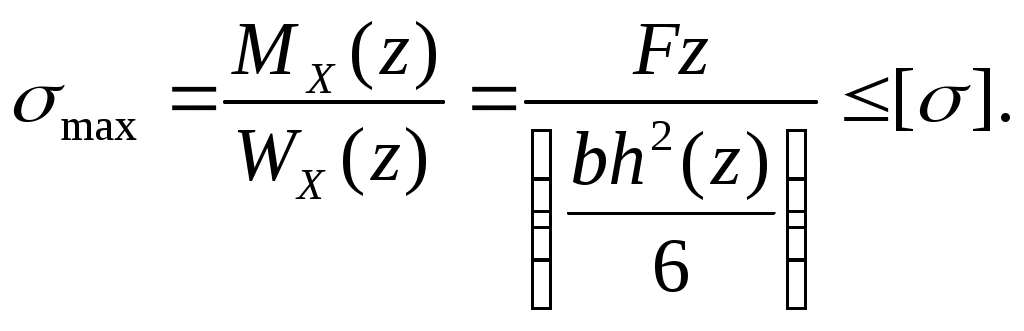
Это условие будет выполнено, если напряжение в произвольном сечении приравнять напряжению в заделке.



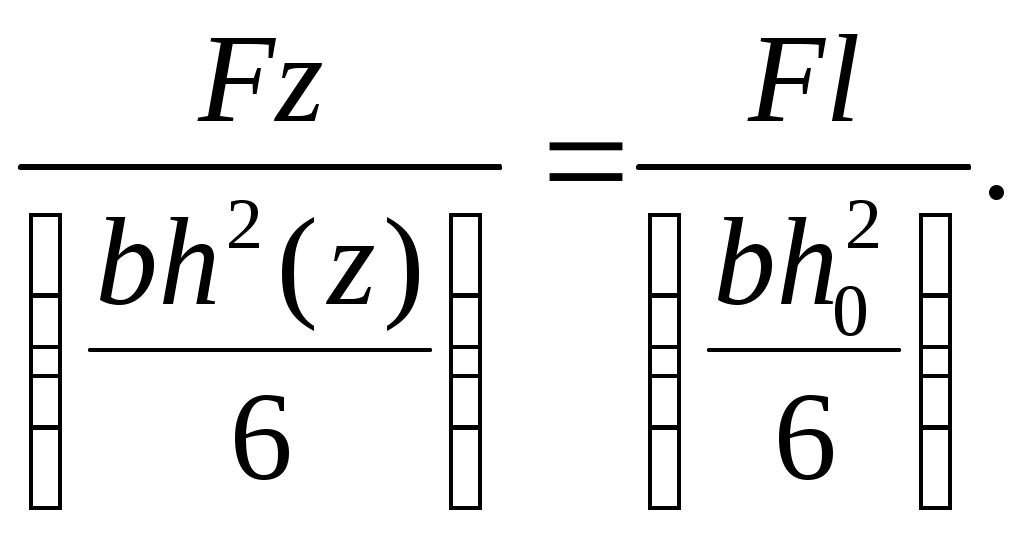
Решая это уравнение относительно h(z), получим



Балки равного сопротивления изгибу, в полном смысле этого слова, на практике встречаются редко. Объясняется это тем, что изготовление таких балок требует больших затрат труда. Однако, в практике часто приходится иметь дело с балками переменного сечения. К таким балкам относятся, например, металлические рессоры.
Вопросы для самопроверки


  1. Какой случай изгиба называется чистым изгибом?

  2. Как можно создать чистый изгиб?

  3. Какие гипотезы положены в основу вывода формулы для вычисления нормальных напряжений при чистом изгибе?

  4. Как связана кривизна осевой линии с изгибающим моментом?

  5. Что такое момент сопротивления сечения при изгибе?

  6. Как можно оценивать рациональность формы поперечного сечения при изгибе?

  7. Почему возникают касательные напряжения в сечениях при поперечном изгибе?

  8. Как выводится формула Журавского?

  9. Что такое траектория главного напряжения, каково её практическое применение?

  10. Почему в двутавровой балке, работающей на изгиб, точка сечения, лежащая в месте перехода от полки к стенке, может оказаться в более опасном напряженном состоянии, чем крайняя точка профиля?

8. Определение перемещений в балках при изгибе

8.1. Общие замечания

Вычисленные напряжения позволяют проверить прочность балок. Однако весьма прочные балки могут оказаться непригодными к эксплуатации из–за недостаточной жесткости. Если балка под нагрузкой сильно прогибается, то при эксплуатации появляются сложности и, кроме того, могут возникнуть значительные колебания с большими амплитудами, а вместе с тем и значительными дополнительные напряжения. Для проверки жесткости балки необходимо научиться определять перемещения отдельных точек её оси.

Смотрите также файлы