Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 388
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
бруса. Вывод универсального уравнения основан на так называемом методе начальных параметров (МНП). По этому методу прогиб в любом сечении балки определяется через перемещения и силовые факторы, взятые в начале координат с учетом приложенной к балке нагрузки.
Представим себе, что на брус действует произвольная система нагрузок, показанная на рис. 8.6.1,а. Представленное направление нагрузок считается положительным. Начало координат совместим с центром тяжести сечения на левом конце балки. Жесткость балки считают постоянной по всей её длине.
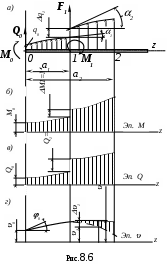
Разобьём балку на участки таким образом, чтобы на протяжении каждого участка изгибающий момент выражался с помощью непрерывной функции:
MI= MI (z);
MII= MII (z).
………………
Рассмотрим первый участок, для которого дифференциальное уравнение имеет вид

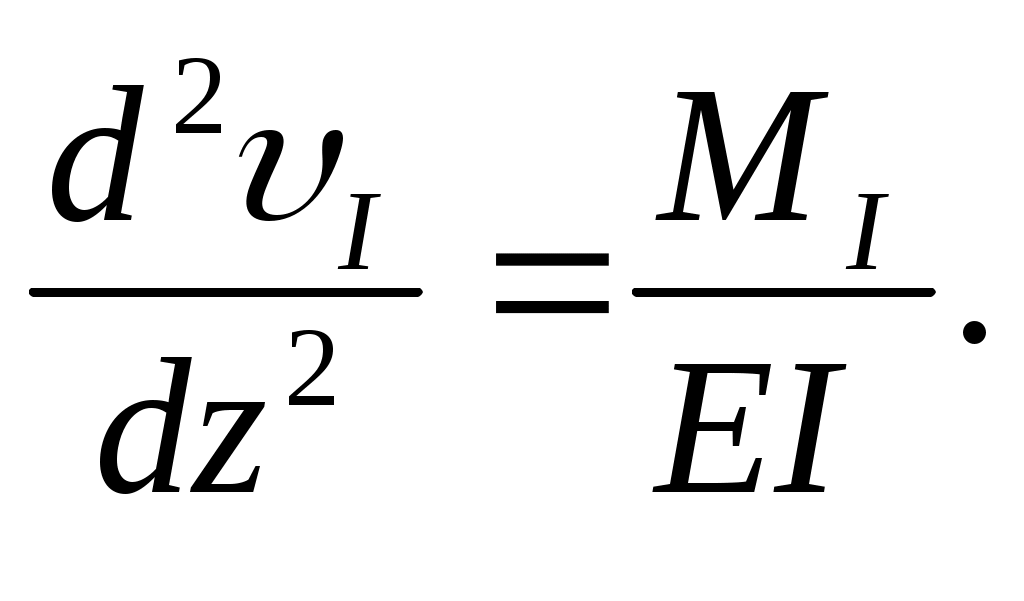 (а)
(а)
Здесь
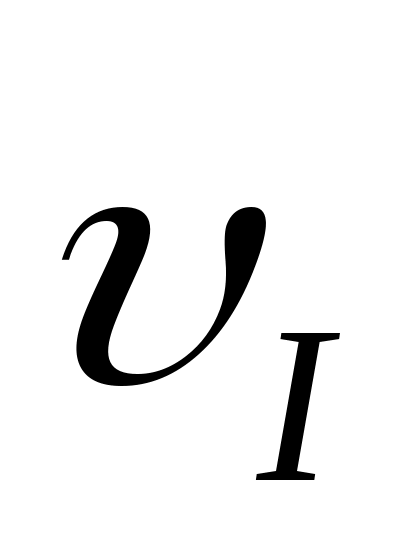 - прогиб в произвольном сечении первого участка;
- прогиб в произвольном сечении первого участка;
МI –функция, выражающая значение изгибающего момента в произвольном сечении первого участка.
Разложим функцию прогиба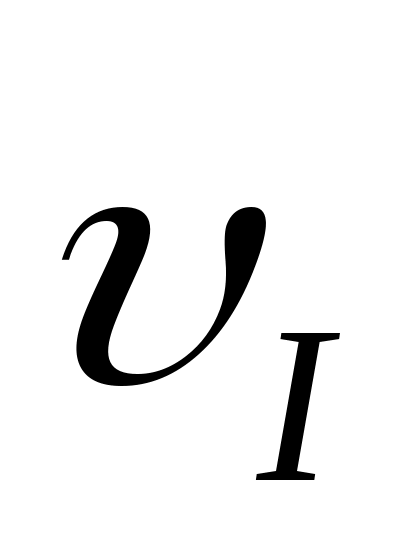 в ряд Маклорена
в ряд Маклорена 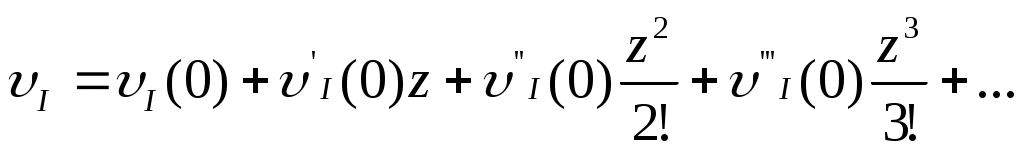 . (б)
. (б)
В этом уравнении величины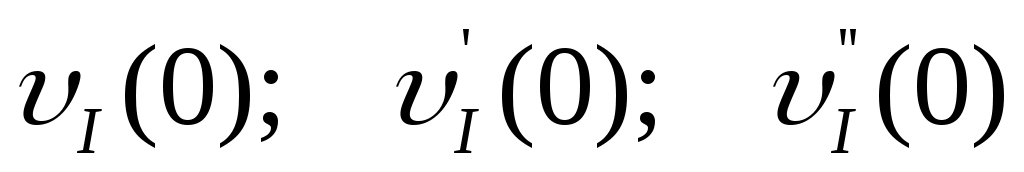 и т. д. представляют собой функцию
и т. д. представляют собой функцию 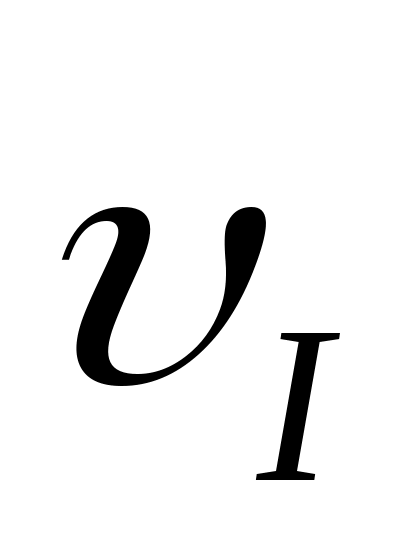 (z) и её производные, взятые в начале координат, т.е. при z = 0. Учтём дифференциальные зависимости:
(z) и её производные, взятые в начале координат, т.е. при z = 0. Учтём дифференциальные зависимости:
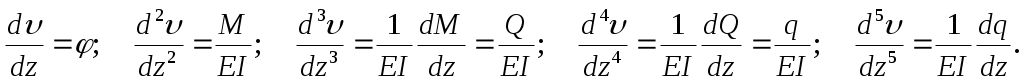 (в)
(в)
Положим z=0 и обозначим:
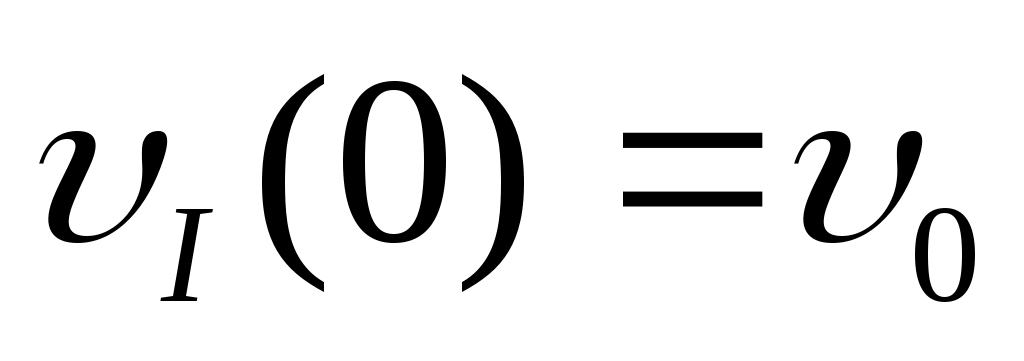 и
и 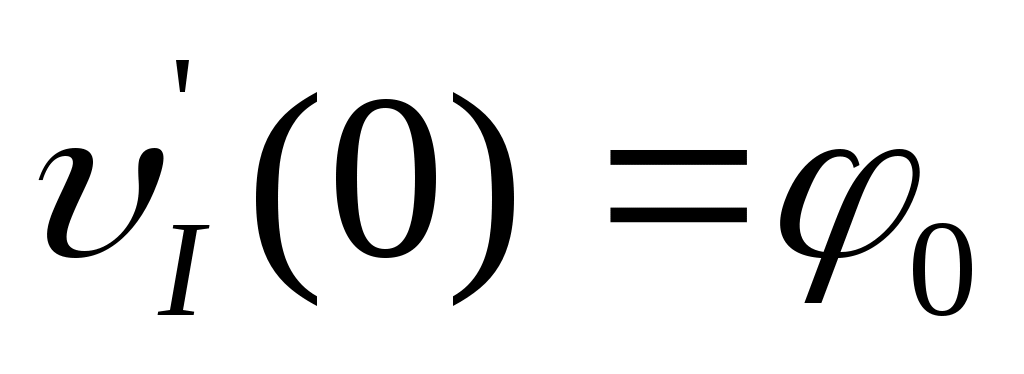 - прогиб и угол поворота в начале координат;
- прогиб и угол поворота в начале координат;
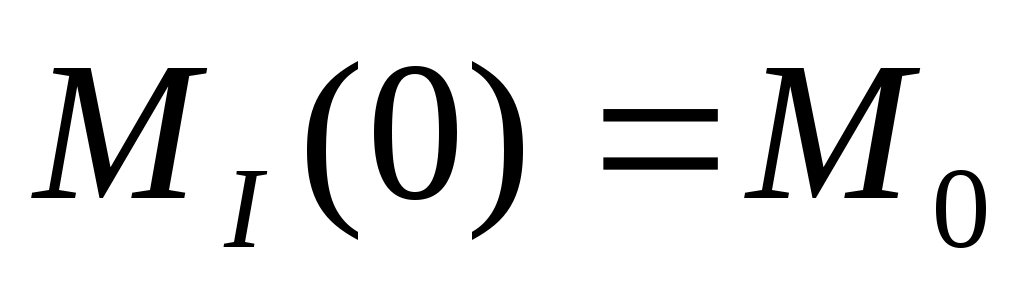
и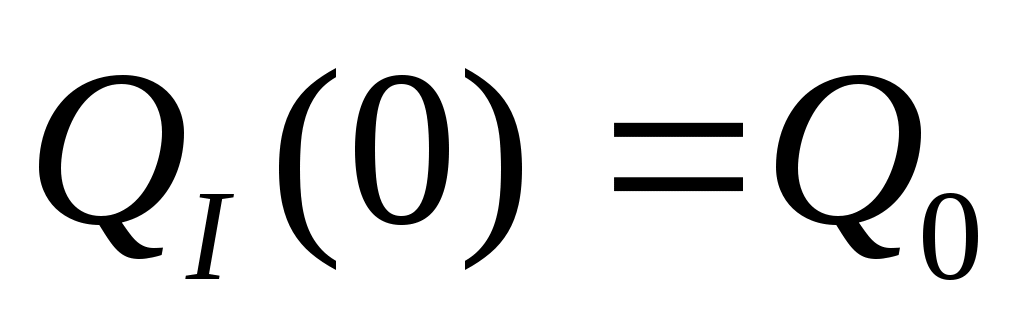 -момент и поперечная сила в сечении, взятые в
-момент и поперечная сила в сечении, взятые в
начале координат;
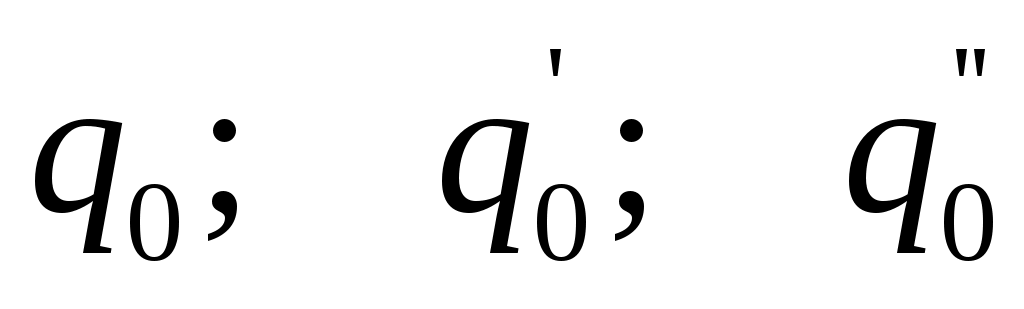 - интенсивность нагрузки и её производные, взятые
- интенсивность нагрузки и её производные, взятые
в начале координат.
Тогда на основании сравнения (б) и (в) имеем следующие равенства:
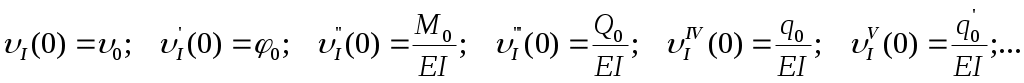 и т.д.
и т.д.
Подставляя эти значения в уравнение (б), получим
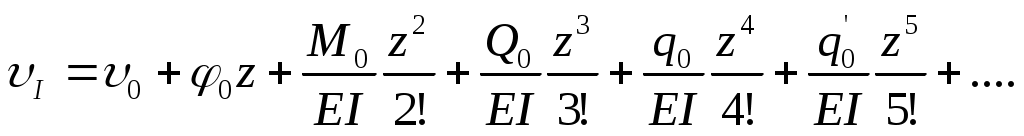 (8.9)
(8.9)
Полученное уравнение позволяет выразить прогибы в любом сечении первого участка через начальные параметры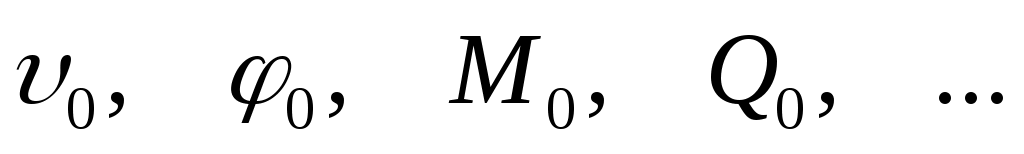 и т.д. Часть этих параметров известна заранее, а часть подлежит определению из граничных условий.
и т.д. Часть этих параметров известна заранее, а часть подлежит определению из граничных условий.
По уравнению (8.9), полученного для первого участка, построим линию прогибов в пределах двух участков. На протяжении первого участка (рис. 3,г) она изображена жирной линией, на протяжении второго участка – пунктиром. Пунктирная линия представляет собой изображение линии, описанной уравнением (8.9), но она не совпадает с истинной кривой оси изогнутого бруса для второго участка, которая проведена жирной линией. Ординаты между двумя указанными кривыми заштрихованы на чертеже. Аналитически эти ординаты выражаются равенством
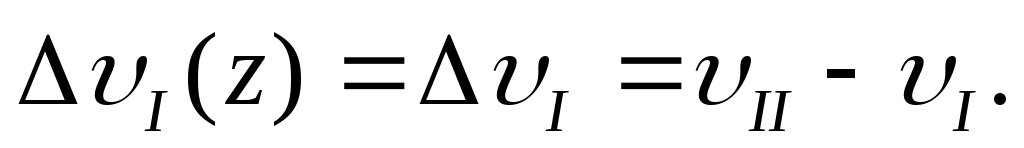 (г)
(г)
Определим величину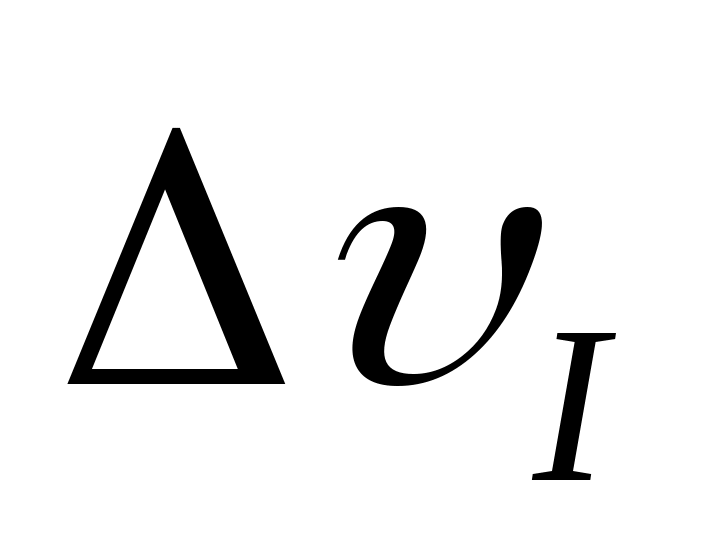 , а затем найдём ординаты прогибов балки на втором участке:
, а затем найдём ординаты прогибов балки на втором участке:
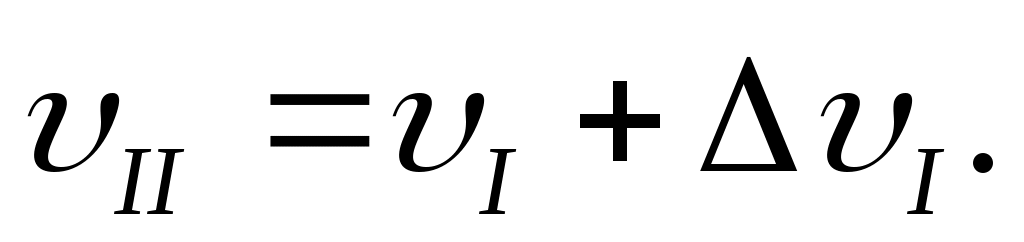 (д)
(д)
Для этой цели напишем два дифференциальных уравнения:
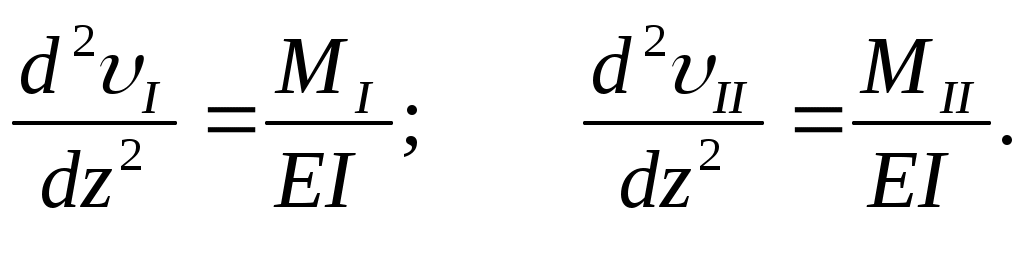
Вычитая первое уравнение из второго, получаем

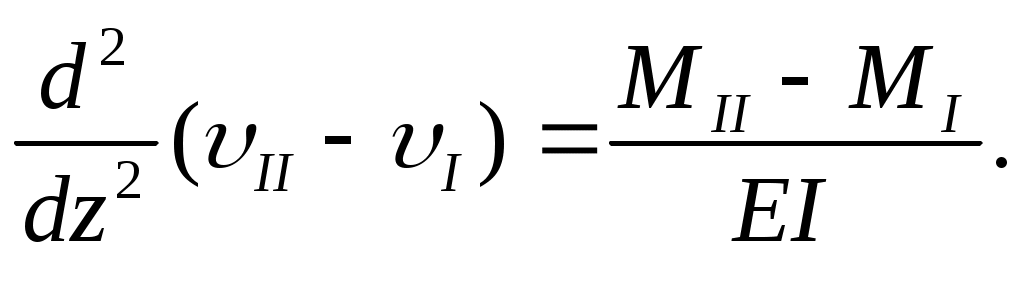
Обозначив
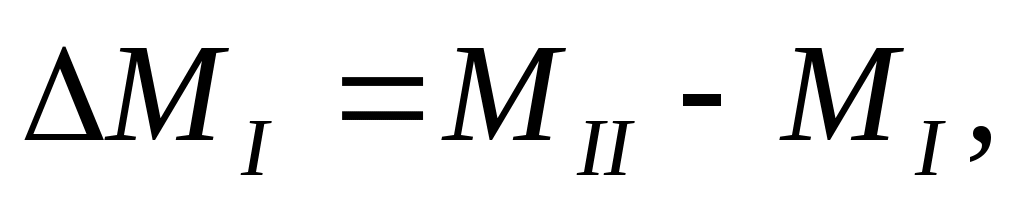
Имеем
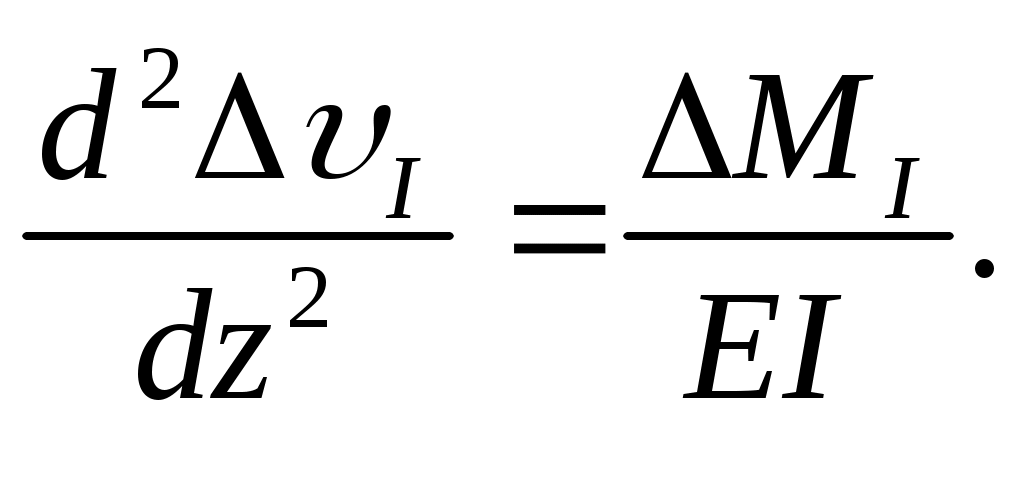
(е)
На основании сходства дифференциального уравнения (е) с основным уравнением (а) можно утверждать, что решение для функции совпадает с решением, полученным для функции (9).
совпадает с решением, полученным для функции (9).
В этом решении вместо координаты z берется координата, отсчитанная от т.1, т.е. (z-а1). Вместо величин M0 , Q0 , q0 , ..., и т.д. необходимо брать М1, Q1, q1 … .
Следовательно,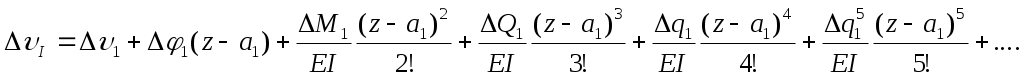 (8.10)
(8.10)
Для непрерывных балок, которые по всей длине, в том числе в т.1, не имеют разрезов и полных шарниров,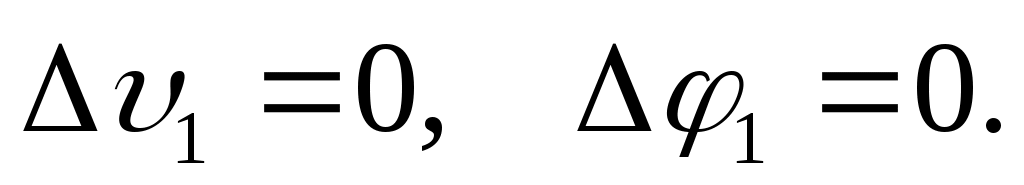
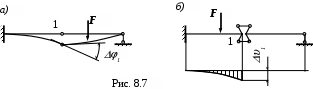
Скачок угла поворота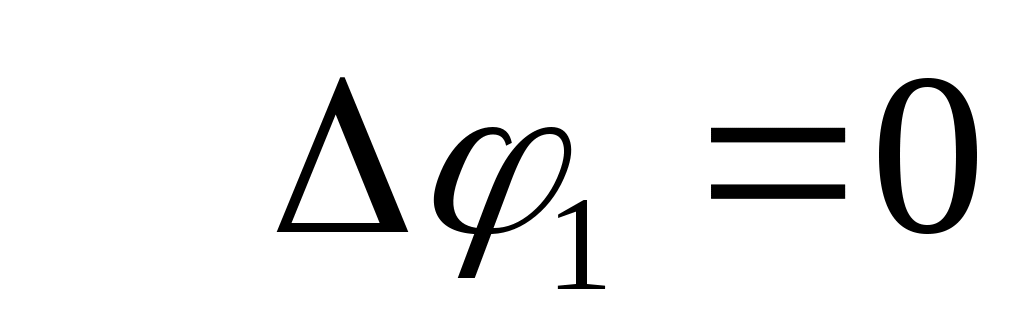 может иметь место в случае, если в точке 1 поставлен шарнир, из-за которого углы поворота слева и справа от точки 1 будут различны (рис. 8.7, а ). Скачок в прогибах возможен, если в точке 1 поставлен сложный шарнир (рис. 8.7, б ).
может иметь место в случае, если в точке 1 поставлен шарнир, из-за которого углы поворота слева и справа от точки 1 будут различны (рис. 8.7, а ). Скачок в прогибах возможен, если в точке 1 поставлен сложный шарнир (рис. 8.7, б ).
Если учесть, что
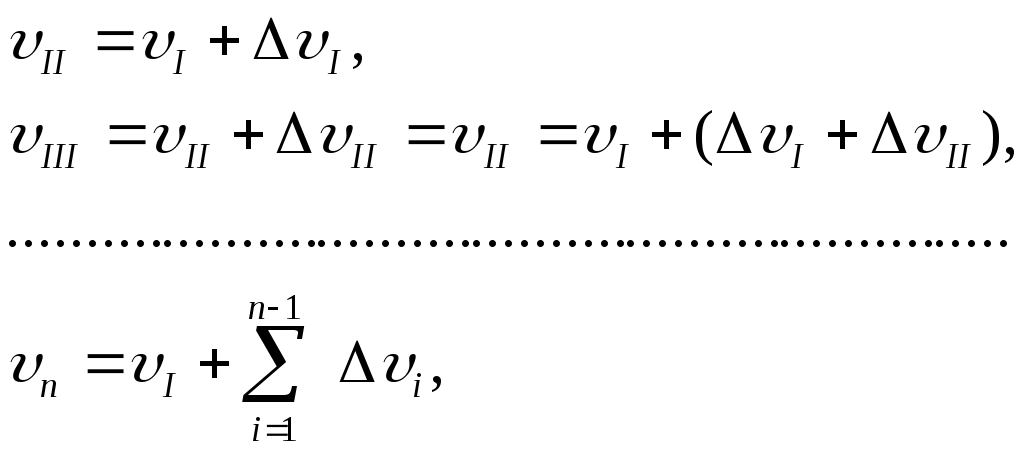 (ж)
(ж)
и вместе с тем воспользоваться уравнениями (8.9) и (8.10), то получим универсальное уравнение прогибов для произвольного участка

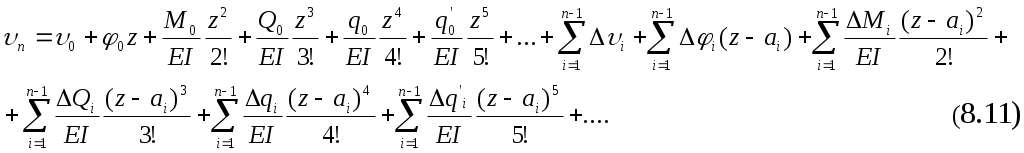
Путем дифференцирования получим универсальное уравнение для углов поворота
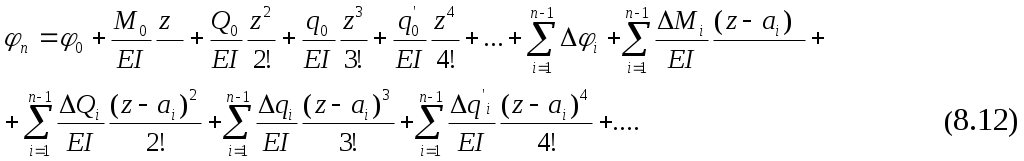
где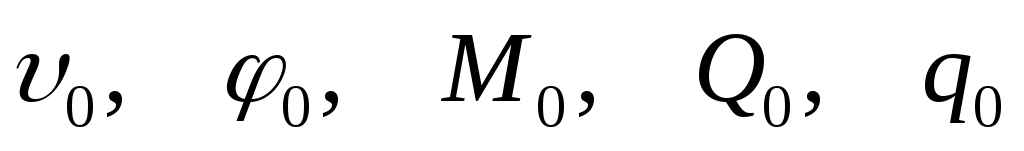 - прогиб, угол поворота, изгибающий момент, поперечная сила, интенсивность поперечной нагрузки в начале координат;
- прогиб, угол поворота, изгибающий момент, поперечная сила, интенсивность поперечной нагрузки в начале координат;
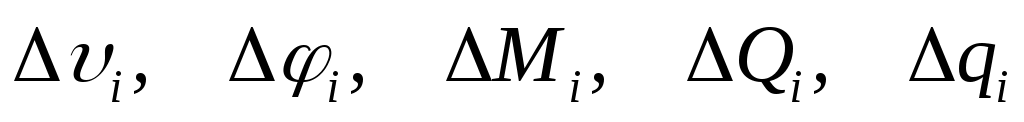 - приращения соответствующих величин на границах участков;
- приращения соответствующих величин на границах участков;
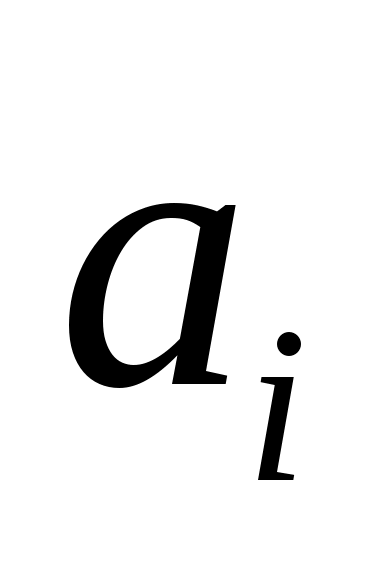
- расстояние от начала координат до начала участка, в котором имеется скачек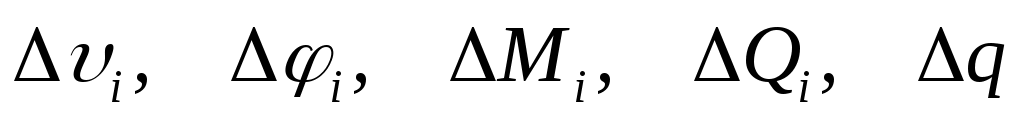 .
.
При решении каких-либо частных задач целый ряд членов, входящих в уравнения (10) и (11), равен нулю.
Полученные уравнения (8.11) и (8.12) зависят от величин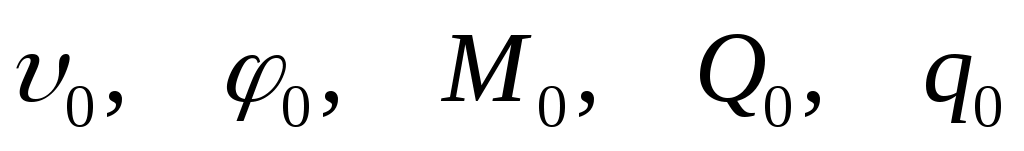 и т.п., которые берутся в начале координат, поэтому метод решения по указанным уравнениям носит название метод начальных параметров (МНП) .
и т.п., которые берутся в начале координат, поэтому метод решения по указанным уравнениям носит название метод начальных параметров (МНП) .
Основное преимущество (МНП) состоит именно в том, что независимо от числа участков и нагрузки число постоянных, которые надо определить в статически определимой балке, не превышает двух.
Для балки, изображенной на рисунке 8.8,а, начальный прогиб и начальный угол поворота равны нулю.
Для случая, представленного на рисунке 8.8,б, начальный прогиб равен нулю, неизвестным остается начальный угол поворота 0, который может быть определим из равенства нулю прогиба на правой опоре.
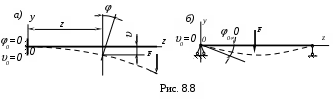
В некоторых случаях ставится вопрос об определении места и величины наибольшего прогиба балки. Для определения местоположения сечения, в котором прогиб приобретает наибольшее значение, необходимо приравнять нулю производную:
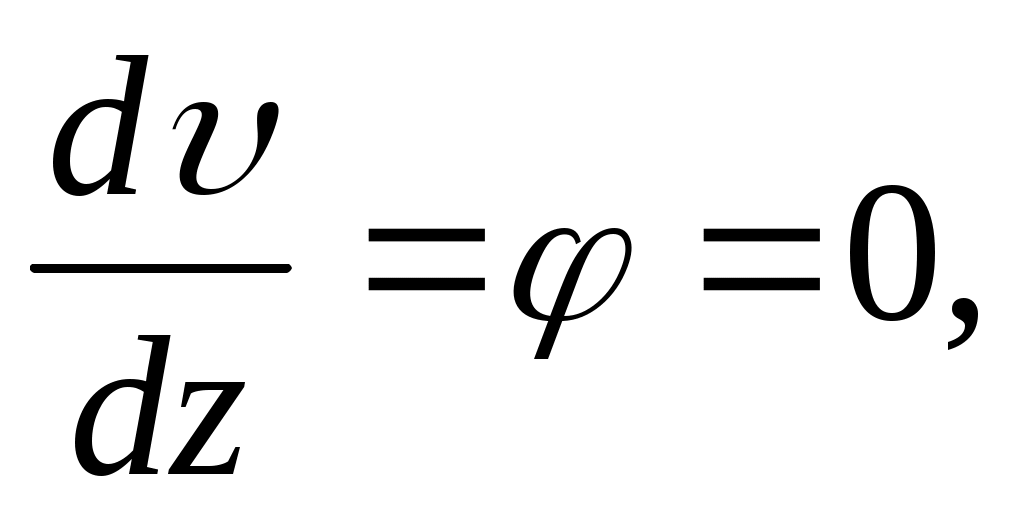 (8.13)
(8.13)
откуда можно определить координату наибольшего прогиба.
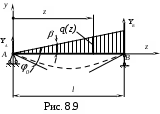 Пример 3. Двухопорная балка загружена треугольной нагрузкой общим весом G.
Пример 3. Двухопорная балка загружена треугольной нагрузкой общим весом G.
1. Составить уравнения прогибов и углов поворота.
2. Найти наибольший прогиб.
Опорные реакции YA=G/3 иYB= 2G/3. Наибольшая интенсивность q1=2G/l, интенсивность в произвольном сечении q(z)=q1(z/l), q(z)=tg=q1/l=2G/l2.
Граничные условия:
При z=0
0=0;
z=ll=0.
Составим уравнения прогибов и углов поворота:
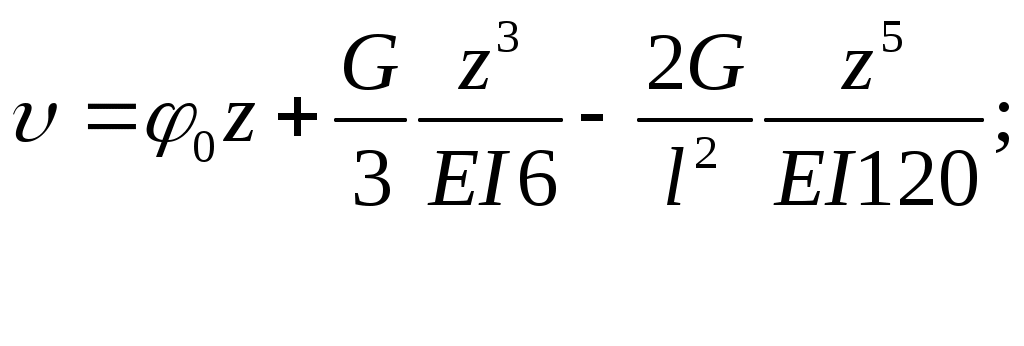
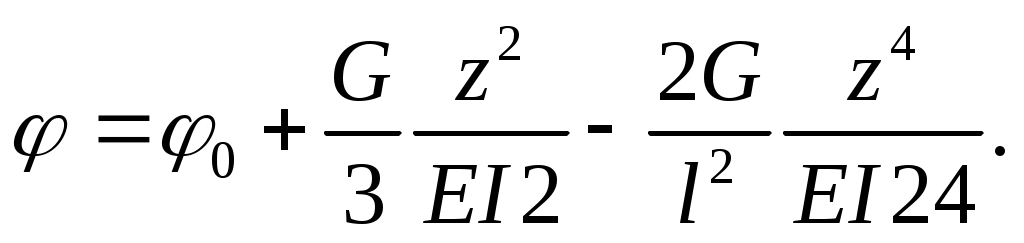
Из условия закрепления для правого конца (z=l, l=0) определяем 0).
0).
Уравнение прогибов




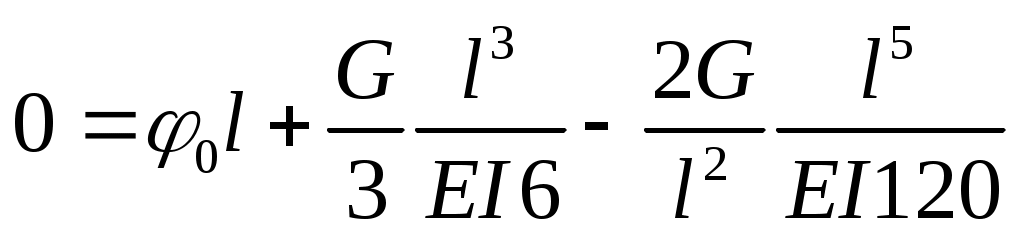 ,
,
откуда находим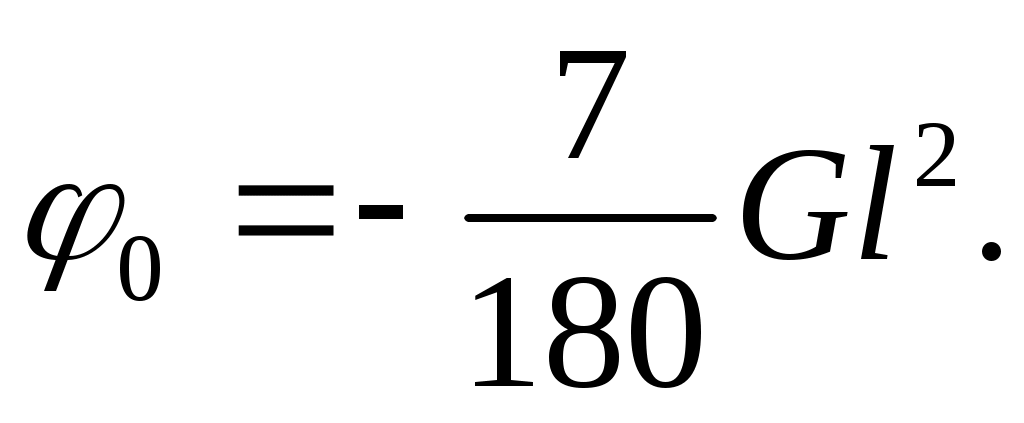
Окончательно, уравнения прогибов и углов поворота имеют вид
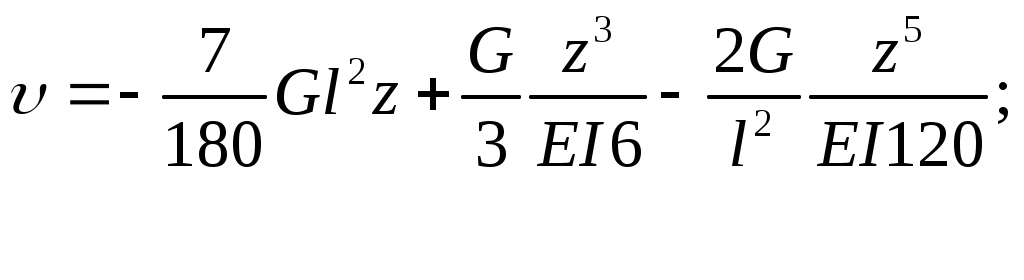
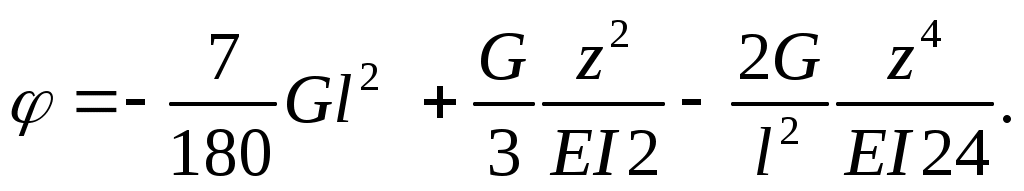
Чтобы найти наибольший прогиб, необходимо учесть, что в этом сечении угол поворота равен нулю. Приравнивая нулю уравнение углов поворота, получаем
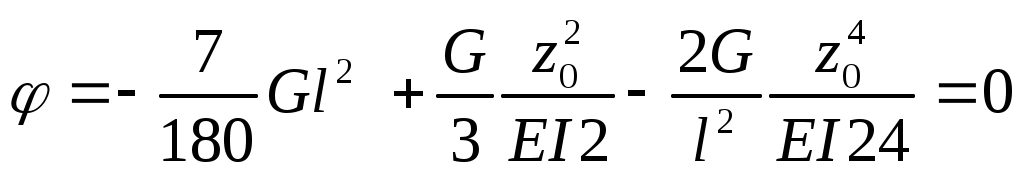
или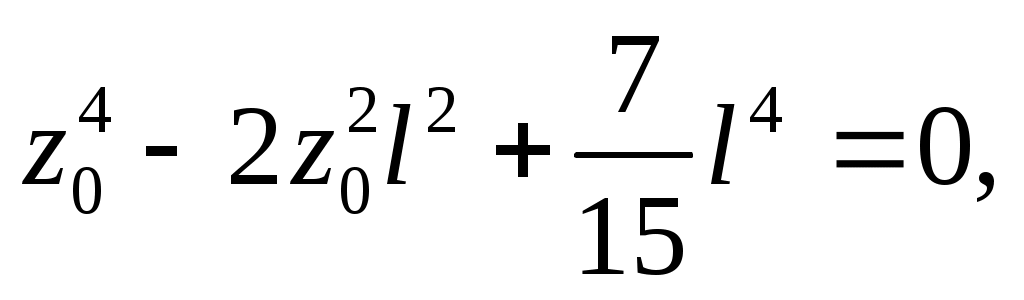
z0=0,52l 0,5l.
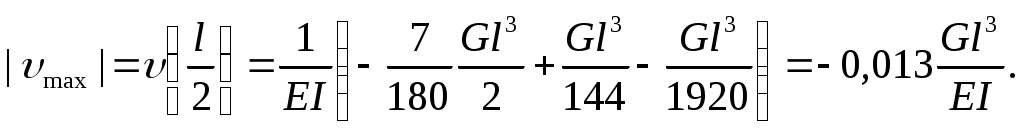
Пример 4. Получить универсальное уравнение прогибов для произвольного участка балки, представленной на рис.8.10.
Определим опорные реакции:

Проверка: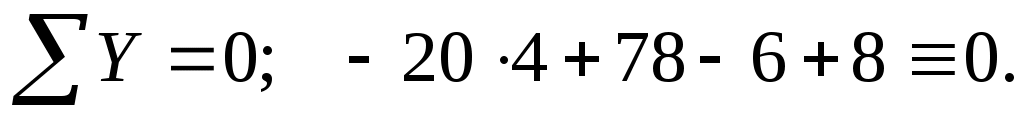
Построим эпюры QYи MX.
При составлении универсального уравнения прогибов рационально выбрать начало отсчета в точке В т.к. прогиб в т.В равен нулю.
Составим уравнение прогибов
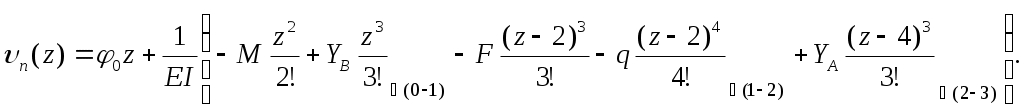
Из условий закрепления балки на опоре
Представим себе, что на брус действует произвольная система нагрузок, показанная на рис. 8.6.1,а. Представленное направление нагрузок считается положительным. Начало координат совместим с центром тяжести сечения на левом конце балки. Жесткость балки считают постоянной по всей её длине.

Разобьём балку на участки таким образом, чтобы на протяжении каждого участка изгибающий момент выражался с помощью непрерывной функции:
MI= MI (z);
MII= MII (z).
………………
Рассмотрим первый участок, для которого дифференциальное уравнение имеет вид
Здесь
МI –функция, выражающая значение изгибающего момента в произвольном сечении первого участка.
Разложим функцию прогиба
В этом уравнении величины
Положим z=0 и обозначим:
и
начале координат;
в начале координат.
Тогда на основании сравнения (б) и (в) имеем следующие равенства:
Подставляя эти значения в уравнение (б), получим
Полученное уравнение позволяет выразить прогибы в любом сечении первого участка через начальные параметры
По уравнению (8.9), полученного для первого участка, построим линию прогибов в пределах двух участков. На протяжении первого участка (рис. 3,г) она изображена жирной линией, на протяжении второго участка – пунктиром. Пунктирная линия представляет собой изображение линии, описанной уравнением (8.9), но она не совпадает с истинной кривой оси изогнутого бруса для второго участка, которая проведена жирной линией. Ординаты между двумя указанными кривыми заштрихованы на чертеже. Аналитически эти ординаты выражаются равенством
Определим величину
Для этой цели напишем два дифференциальных уравнения:
Вычитая первое уравнение из второго, получаем
Обозначив
Имеем
(е)
На основании сходства дифференциального уравнения (е) с основным уравнением (а) можно утверждать, что решение для функции
В этом решении вместо координаты z берется координата, отсчитанная от т.1, т.е. (z-а1). Вместо величин M0 , Q0 , q0 , ..., и т.д. необходимо брать М1, Q1, q1 … .
Следовательно,
Для непрерывных балок, которые по всей длине, в том числе в т.1, не имеют разрезов и полных шарниров,
Скачок угла поворота

Если учесть, что
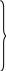
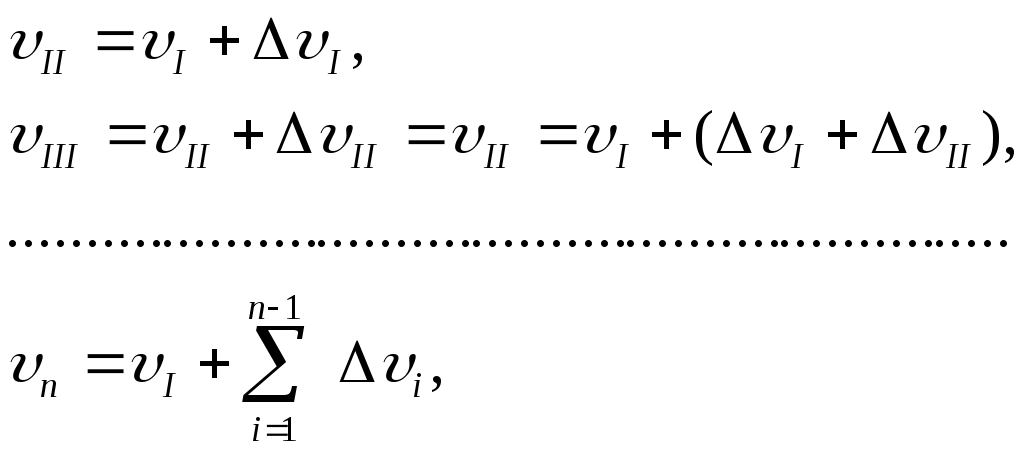 (ж)
(ж)и вместе с тем воспользоваться уравнениями (8.9) и (8.10), то получим универсальное уравнение прогибов для произвольного участка
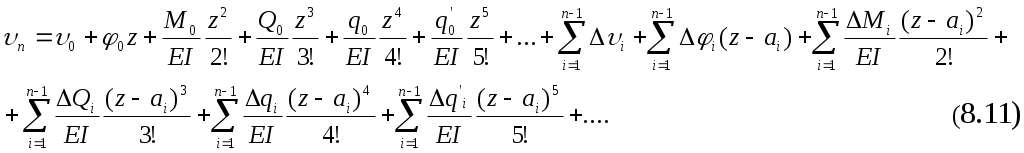
Путем дифференцирования получим универсальное уравнение для углов поворота
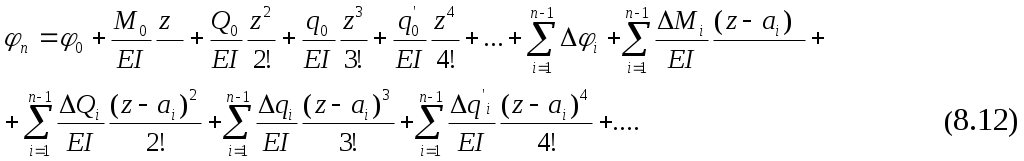
где
- расстояние от начала координат до начала участка, в котором имеется скачек
При решении каких-либо частных задач целый ряд членов, входящих в уравнения (10) и (11), равен нулю.
Полученные уравнения (8.11) и (8.12) зависят от величин
Основное преимущество (МНП) состоит именно в том, что независимо от числа участков и нагрузки число постоянных, которые надо определить в статически определимой балке, не превышает двух.
Для балки, изображенной на рисунке 8.8,а, начальный прогиб и начальный угол поворота равны нулю.
Для случая, представленного на рисунке 8.8,б, начальный прогиб равен нулю, неизвестным остается начальный угол поворота 0, который может быть определим из равенства нулю прогиба на правой опоре.
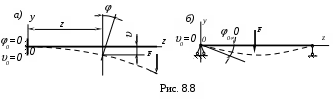
В некоторых случаях ставится вопрос об определении места и величины наибольшего прогиба балки. Для определения местоположения сечения, в котором прогиб приобретает наибольшее значение, необходимо приравнять нулю производную:
откуда можно определить координату наибольшего прогиба.
 Пример 3. Двухопорная балка загружена треугольной нагрузкой общим весом G.
Пример 3. Двухопорная балка загружена треугольной нагрузкой общим весом G.1. Составить уравнения прогибов и углов поворота.
2. Найти наибольший прогиб.
Опорные реакции YA=G/3 иYB= 2G/3. Наибольшая интенсивность q1=2G/l, интенсивность в произвольном сечении q(z)=q1(z/l), q(z)=tg=q1/l=2G/l2.
Граничные условия:
При z=0
0=0;
z=ll=0.
Составим уравнения прогибов и углов поворота:
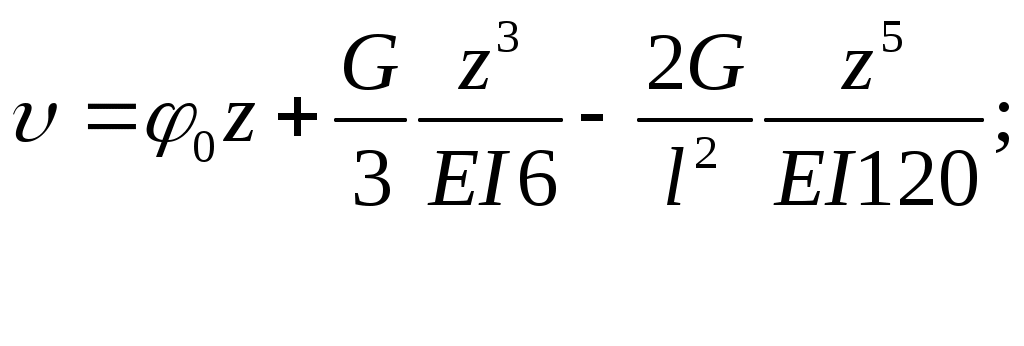
Из условия закрепления для правого конца (z=l, l=0) определяем
Уравнение прогибов
откуда находим
Окончательно, уравнения прогибов и углов поворота имеют вид
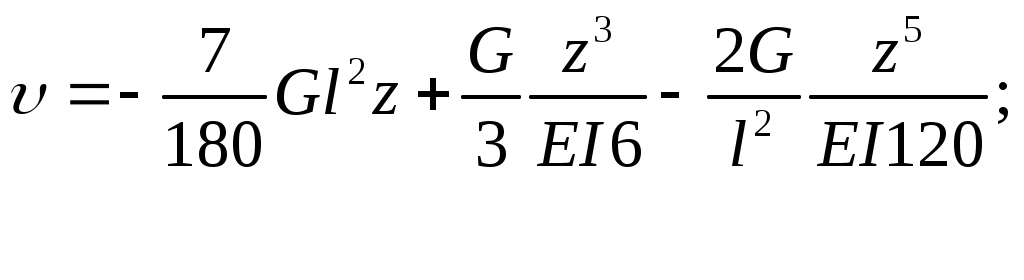
Чтобы найти наибольший прогиб, необходимо учесть, что в этом сечении угол поворота равен нулю. Приравнивая нулю уравнение углов поворота, получаем
или
z0=0,52l 0,5l.
Пример 4. Получить универсальное уравнение прогибов для произвольного участка балки, представленной на рис.8.10.
Определим опорные реакции:
Проверка:
Построим эпюры QYи MX.
При составлении универсального уравнения прогибов рационально выбрать начало отсчета в точке В т.к. прогиб в т.В равен нулю.
Составим уравнение прогибов
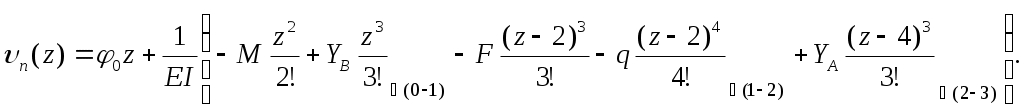
Из условий закрепления балки на опоре