Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 401
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
Сх через , учитывая, что
tg=My/Mx
п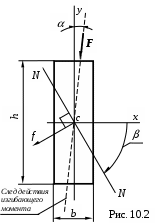
олучим положение нулевой линии (N-N) 
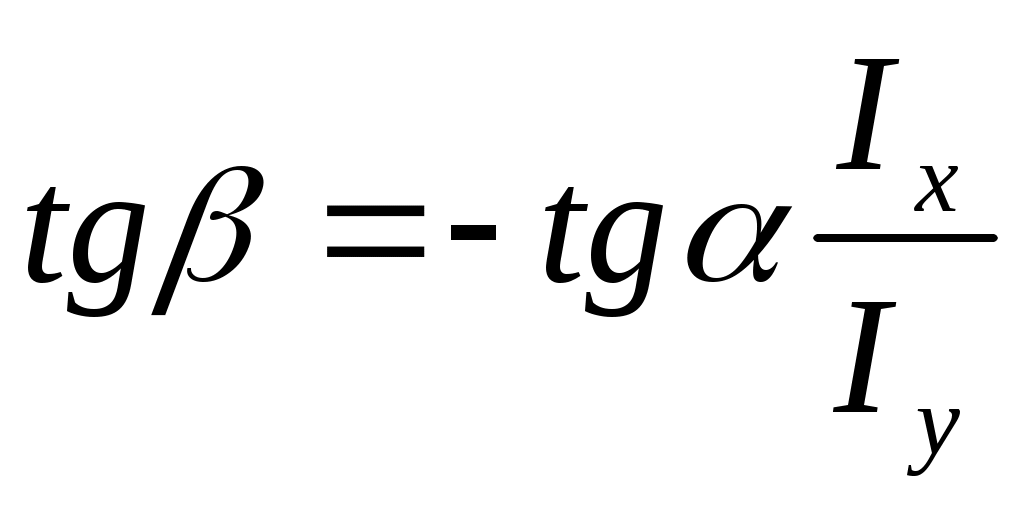(10.3)
Исторически угол , определяющий положение плоскости действия сил (изгибающего момента М), откладывают от вертикали (рис. 11.2.), т. е. от оси у, тогда знак (-)будет указывать на то, что угол надо отложить от оси х в том же направлении.
Как видно из уравнения (10.3), нулевая линия не перпендикулярна силовой линии. Углы между этими линиями тем больше отличаются друг от друга, чем больше разница между двумя главными моментами инерции. Только в тех сечениях, у которых моменты инерции относительно обеих осей равны друг другу (круглого, квадратного и др.), нулевая и силовая линии пересекаются под углом 900.
Пример 2. Рассмотрим поперечное сечение бруса в форме прямоугольника соотношением сторон h/b=5 (рис. 10.2), для которого
.
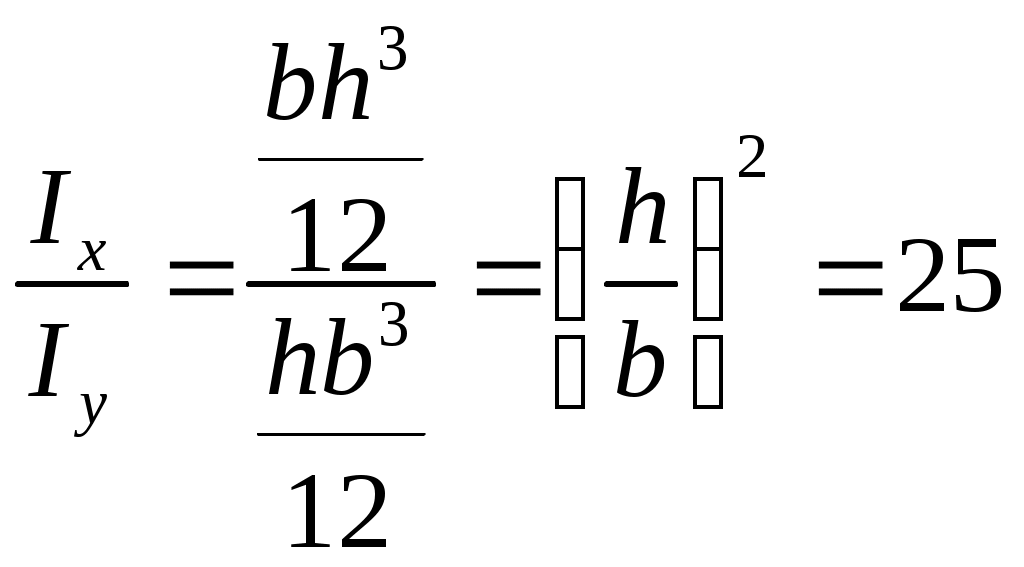В этом случае, например, при =50, tg=-25tg=-250,0875=-2,19; =650.
Положение нейтральной линии (оси) N-N для этого случая показано на рисунке10.2.
Нормальные напряжения при косом изгибе, так же как и в случае прямого изгиба, прямо пропорциональны расстоянию от этой точки до нейтральной оси.
Перемещение f перпендикулярно нейтральной оси и, следовательно, не совпадает с плоскостью действия нагрузки (на рисунке след действия изгибающего момента).
Пример 3. В частном случае, когда для бруса прямоугольного сечения силовая линия проходит по одной из диагоналей (рис. 10.3.),
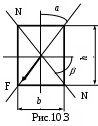
tg=-(h/b)[(bh3/12)/(hb3)/12]=-h/b.
Получив положение нулевой линии (N-N), находим наиболее напряжённые точки, как наиболее удалённые от неё. Подставим в формулу (10.1) координаты этих точек и учтем, что Mx=McosMy=Msin. Тогда условие прочности получит вид:
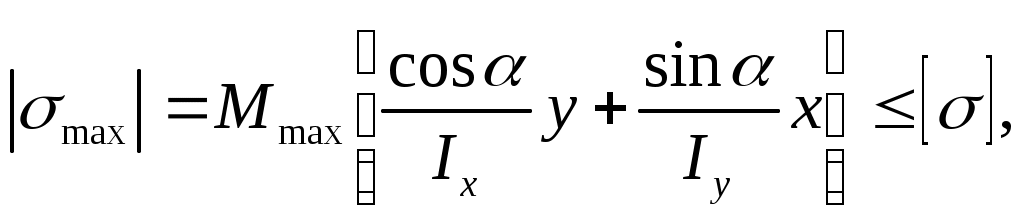
(10.4)
где х и у – координаты точки, наиболее удалённой от нейтральной линии (оси).
Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр) формула (10.4) упрощается
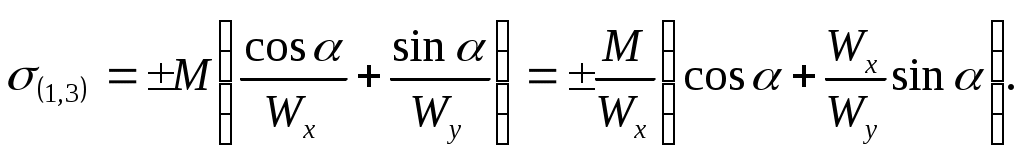(10.5)
Условие прочности для таких сечений примет вид:
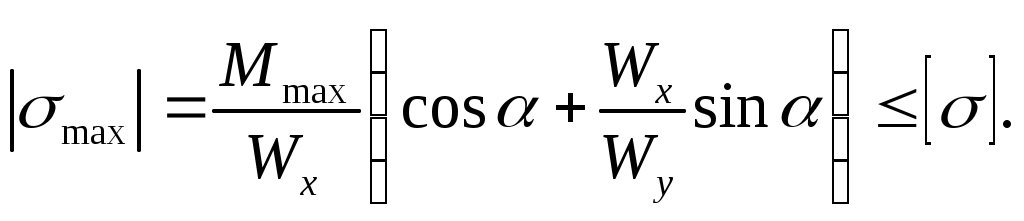(10.6)
При подборе сечений приходится задаваться отношением Wx/Wy и,
зная [], Mmax и угол , путём последовательных попыток искать значения Wx и Wy, удовлетворяющие условию прочности (10.6).
10.2.1.2. Прогибы при косом изгибе.
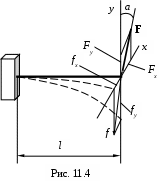
Разложим силу F (рис. 10.4), на составляющие Fxи Fy.
Найдём отдельно прогибы от этих составляющих. Обозначив прогибы конца консоли длиной l по направлению осей х и у через fx и fy имеем:
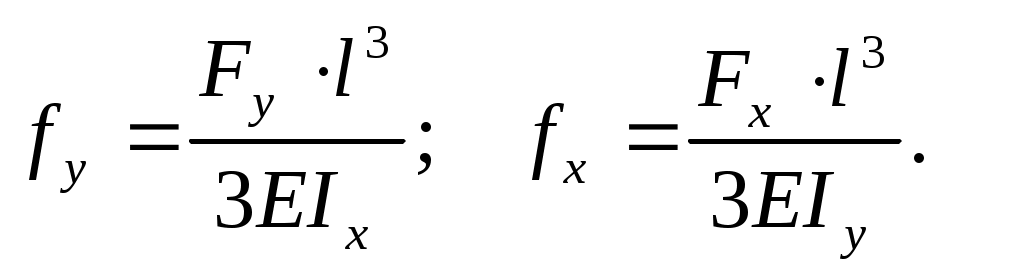
Суммарный прогиб можно найти как геометрическую сумму: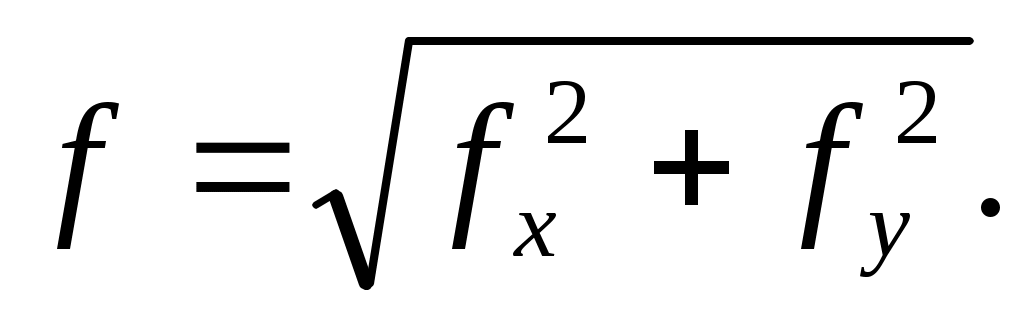
Найдём теперь направление суммарного перемещения. Для этого определим значение угла наклона этого перемещения к вертикали:
.
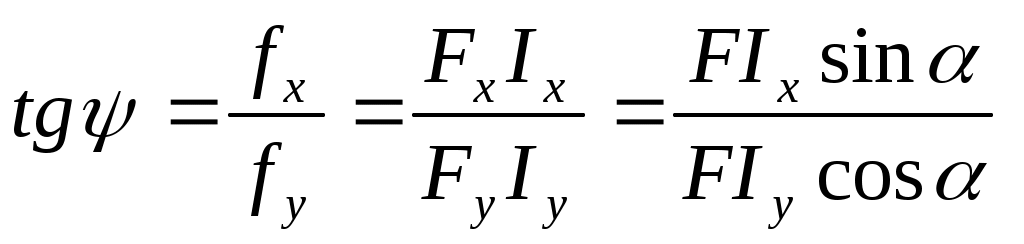Таким образом,
.
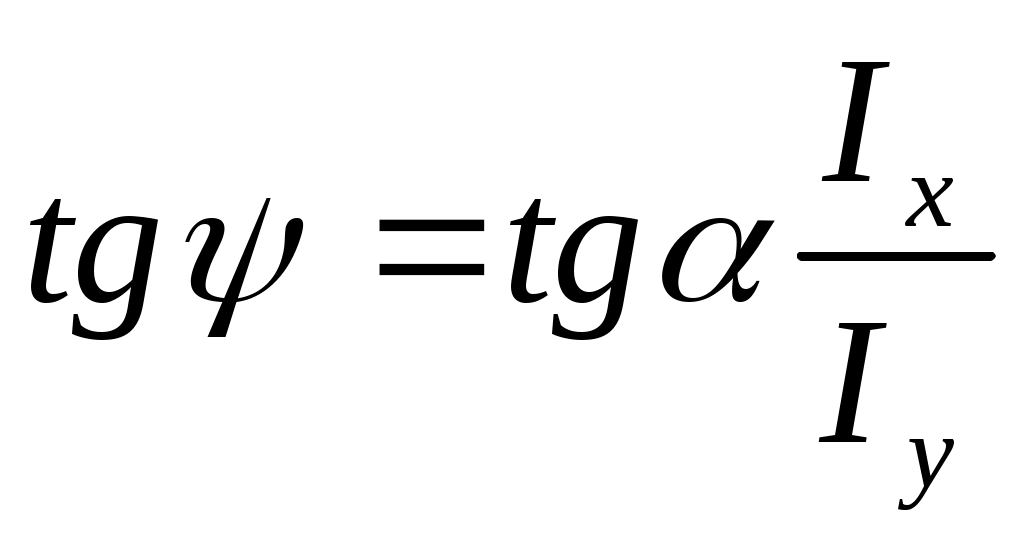Полученная формула идентична с формулой (10.3). Это позволяет сделать заключение, что | | ||
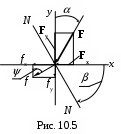
Следовательно (рис. 10.5), направление прогибов f перпендикулярно нулевой линии (N-N).
Вместе с тем отсюда вытекает важное условие, что направление прогибов не совпадает с направлением действующей силы.
В случаях действия пространственной системы сил ось изогнутого стержня представляет собой пространственную кривую.
Такая задача очень часто встречается при расчете опор мостов, фундаментов под насосы и станки и т.д. Рассмотрим действие на стержень двух равных и противоположных сил
F (рис. 10.6), направленных по прямой АА, параллельной оси стержня CC. Расстояние точки А от центра тяжести сечения СА=е называется эксцентриситетом.
Сделаем параллельный перенос сил из точек А в центр тяжести сечения С.
С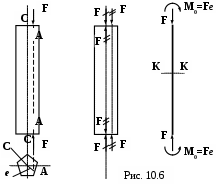
илы, зачёркнутые один раз, вызовут осевое сжатие, а пары сил, зачёркнутые дважды, вызовут чистый изгиб моментами M0=Fe. Так как плоскость действия изгибающих пар СА может не совпадать ни с одной из главных плоскостей инерции стержня, то в общем случае имеет место комбинация продольного сжатия и чистого косого изгиба.
Так как при осевом сжатии и чистом изгибе напряжения во всех сечениях одинаковы, то проверку прочности можно провести для любого сечения,
хотя бы К-К.
Рассмотрим случай внецентренного сжатия массивной колонны. Предположим, что сжимающая сила F (см. рис. 10.7.) приложена в точке К, которая имеет координаты xF и yF, отсчитанные относительно главных центральных осей инерции.
От этой силы в произвольном сечении стержня (колонны), при параллельном переносе сил в центр тяжести сечения (точка С), возникают продольная сжимающая сила N = -F и два изгибающих момента, которые вызывают сжатие в точках, лежащих в первой четверти:
Mx=-FyF ;
My=-FxF .
Напряжение в произвольной точке М, лежащей в положительной четверти произвольного поперечного сечения, равно
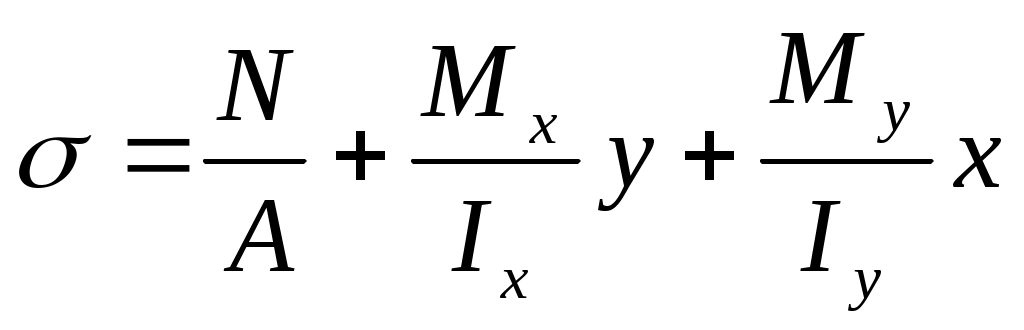. (10.7)
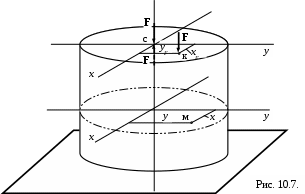
По формуле (1) можно найти напряжение в любой точке сжатой колонны; для этого необходимо величины х и у брать с учётом знака.
Пример. Определить напряжения и построить их эпюру в поперечном сечении колонны (см. рис. 11.8.).
Найдём изгибающие моменты:
Мх=80000 . 0.2=16000 Нм;
Му=80000 .0.15=12000 Нм.
Геометрические характеристики сечения:
площадь сечения
А=0.40.3=0.12 м2;
моменты сопротивления:
Wx=0.3(0.4)2/6=0.008 м3;
Wy=0.4(0.3)2/6=0.006 м3.
Найдём напряжения в четырех угловых точках поперечного сечения:
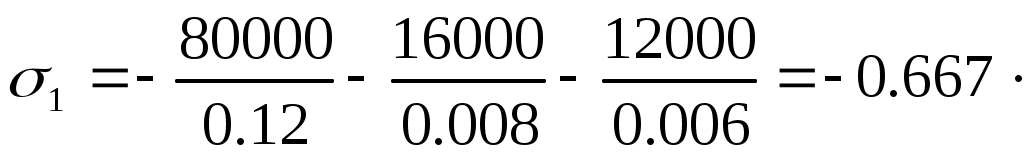106-2-2. Па
-220. Па
3223.33 Па
4+2-20. Па.
По этим значениям построена эпюра напряжений.
10.3.2. Определение положения нулевой линии
Для того чтобы определить положение нулевой линии, преобразуем формулу (10.7). Подставим в эту формулу значение моментов, получим
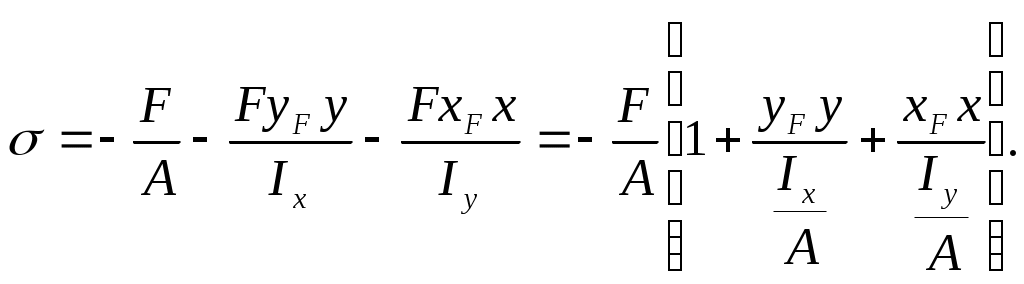
Величины, стоящие в знаменателе второго и третьего слагаемых, представляют собой квадраты радиусов инерции сечения, т.е.
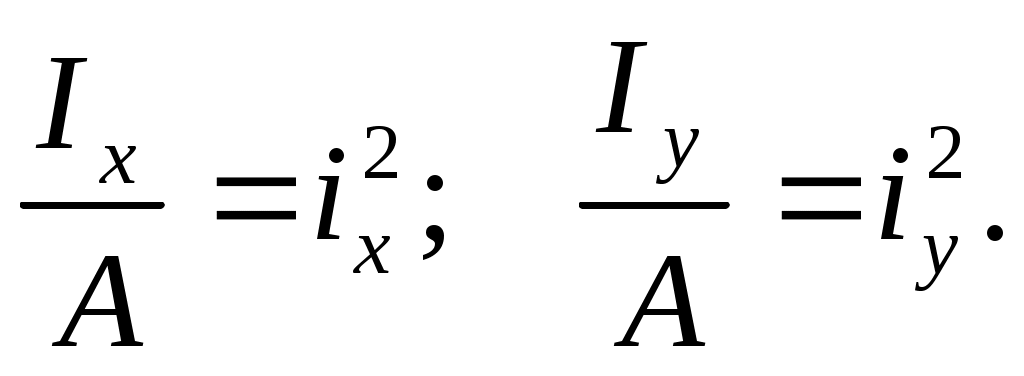
Следовательно,
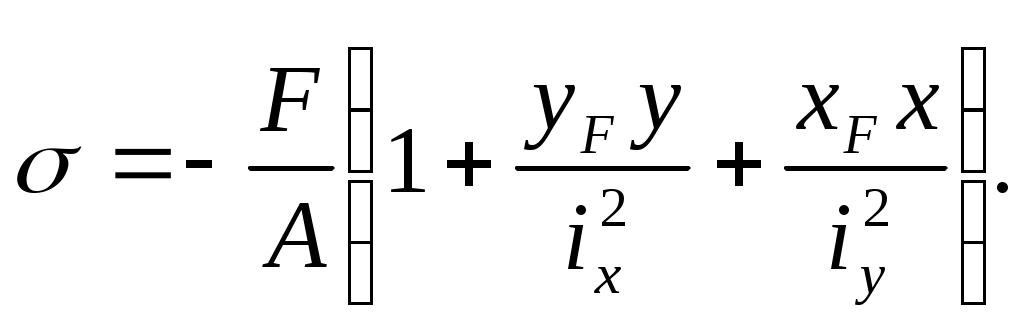(10.8)
Этой формулой, так же как и формулой (10.7), можно пользоваться для определения напряжений в любой точке поперечного сечения колонны. Обозначим координаты любой точки нулевой линии xN и yN . Если эти координаты поставить в уравнение (10.8) и учесть, что напряжения в нулевых точках равны нулю, то после сокращения на величину F/A получим уравнение нулевой линии
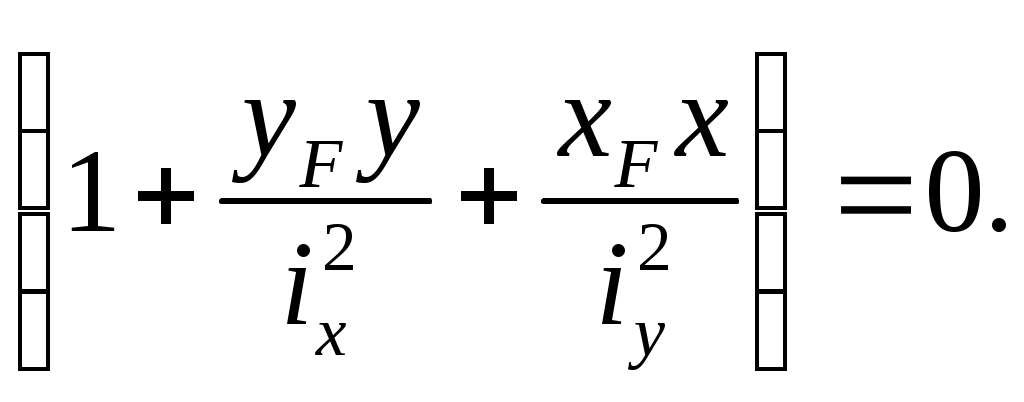(10.9)
По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат.
О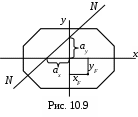
бозначим эти отрезки через ах и ау (см. рис. 10.9) .
Если положить xN=0, yN=ау, то из уравнения (10.9) получим
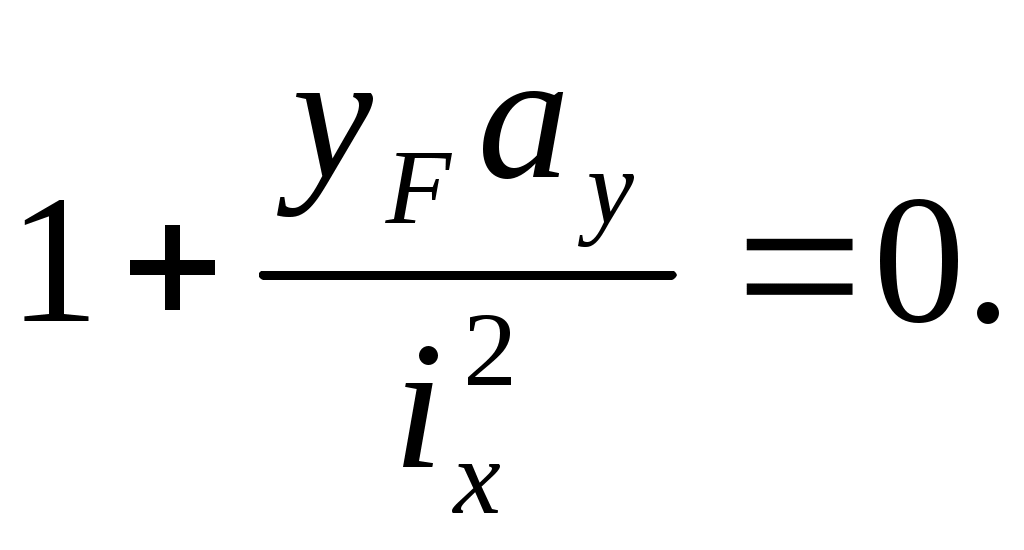
Точно так же для yN=0, xN=ax имеем
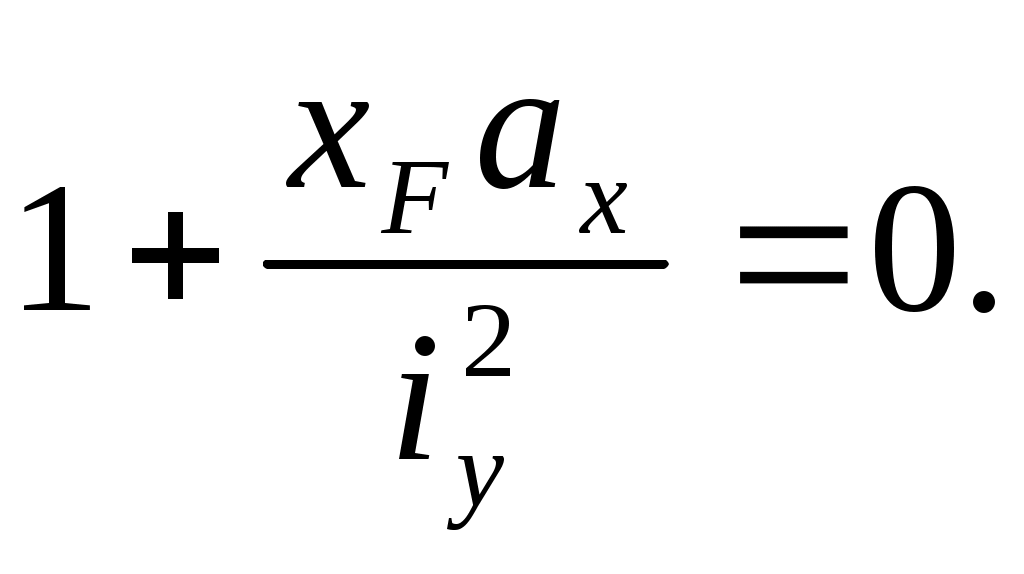
Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на осях координат:
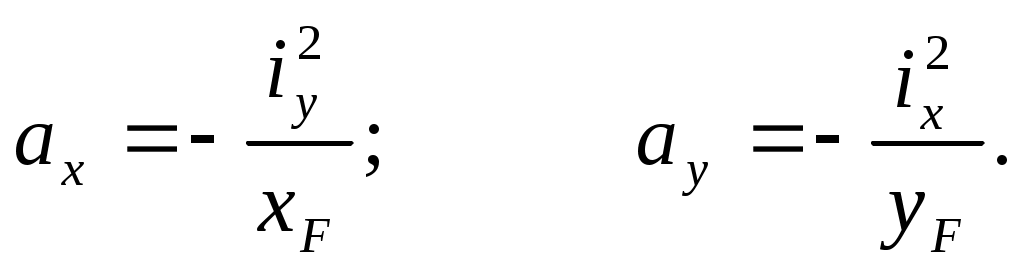
(10.10)
Можно решить обратную задачу, выразив координаты точки приложения силы F при заданных отрезках, отсекаемых нулевой линией на осях координат:
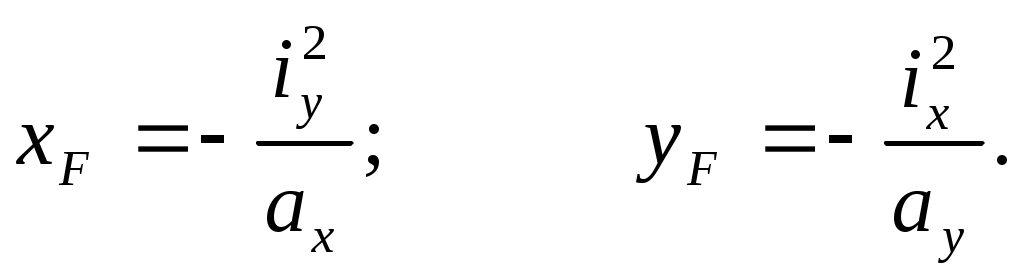(10.11)
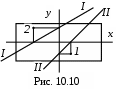
Отметим зависимость величин xF и ax , а также yF иay. Если силу приложить в точке с координатами ах и ау, то нулевая линия отсечёт отрезки на осях координат, равные соответственно xF и yF. Если сила приложена в т.1(рис. 10.10), а соответствующая нулевая линия I-I, то при силе в т.2, нулевая линия займёт положение II-II.
Рассмотрим некоторые характерные особенности, связанные с поведением нулевой линии при различных положениях силы F.
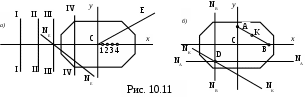
Если сила F приложена в точке, лежащей на оси Су (рис.10.11,а), то
нулевая линия отсекает на оси Сх отрезок, равный бесконечности:
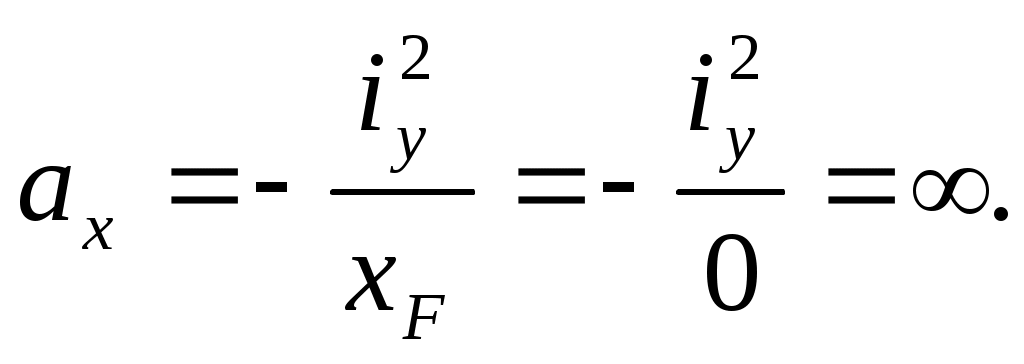
Это означает, что нулевая линия будет параллельна оси Сх.
Представим себе, что сила F перемещается по оси Сх от центра тяжести С к краю сечения. В этом случае нулевая линия перемещается из бесконечности по направлению к сечению, оставаясь при этом всё время параллельной оси Су. Точно как же если сила перемещается по оси Су, то нулевая линия перемещается поступательно, оставаясь всё время параллельной оси Сх.
Так, например, когда сила последовательно приложена в точках 1, 2, 3, 4,
(рис. 11.11, а)), нулевая линия соответственно занимает положения I-I, II-II, III-III и т.д.
Рассмотрим случай, когда сила F перемещается по некоторой прямой СЕ, проходящей через центр тяжести сечения, но не совпадающей ни с одной из главных осей инерции. В этом случае нулевая линия будет также перемещаться параллельно самой себе. В самом деле, из отношения
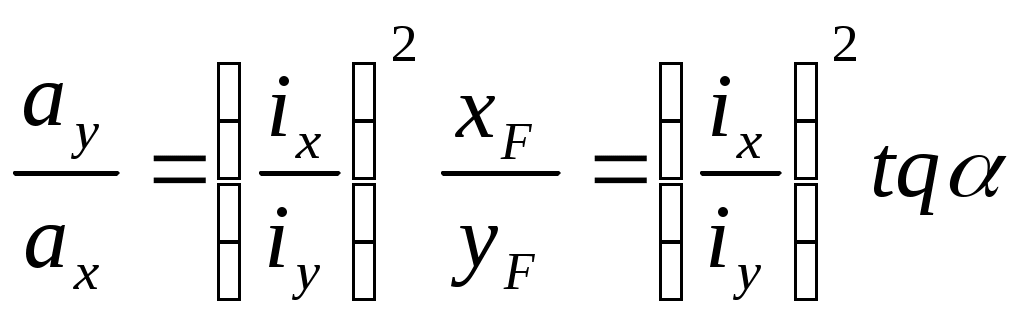
можно сделать вывод, что тангенс угла наклона нулевой линии ау /ax не зависит от численного значения координат точки приложения силы, а зависит от их отношения.
Рассмотрим случай, когда сила F перемещается по некоторой прямой
tg=My/Mx
п
олучим положение нулевой линии (N-N) (10.3)Исторически угол , определяющий положение плоскости действия сил (изгибающего момента М), откладывают от вертикали (рис. 11.2.), т. е. от оси у, тогда знак (-)будет указывать на то, что угол надо отложить от оси х в том же направлении.
Как видно из уравнения (10.3), нулевая линия не перпендикулярна силовой линии. Углы между этими линиями тем больше отличаются друг от друга, чем больше разница между двумя главными моментами инерции. Только в тех сечениях, у которых моменты инерции относительно обеих осей равны друг другу (круглого, квадратного и др.), нулевая и силовая линии пересекаются под углом 900.
Пример 2. Рассмотрим поперечное сечение бруса в форме прямоугольника соотношением сторон h/b=5 (рис. 10.2), для которого
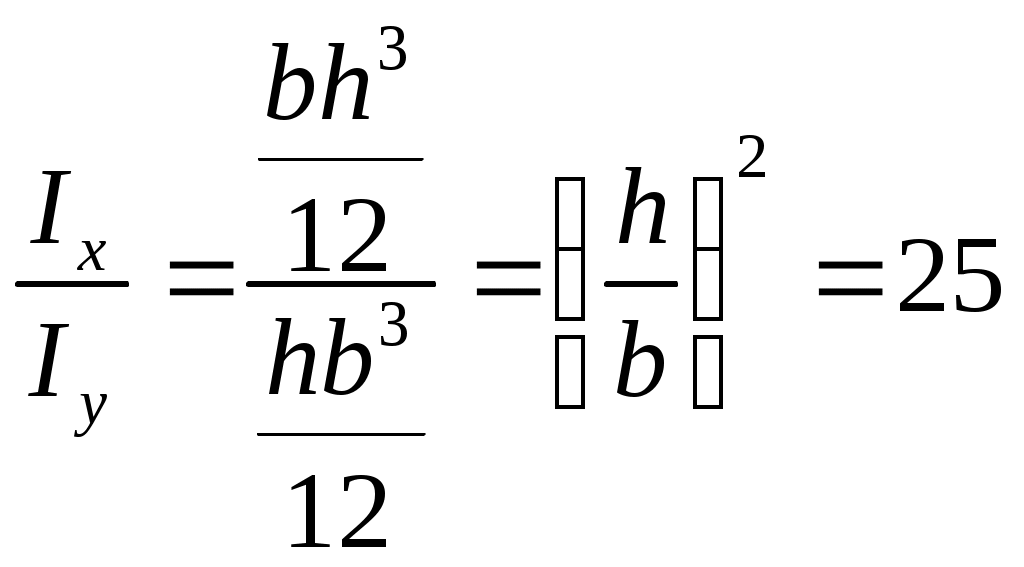.В этом случае, например, при =50, tg=-25tg=-250,0875=-2,19; =650.
Положение нейтральной линии (оси) N-N для этого случая показано на рисунке10.2.
Нормальные напряжения при косом изгибе, так же как и в случае прямого изгиба, прямо пропорциональны расстоянию от этой точки до нейтральной оси.
Перемещение f перпендикулярно нейтральной оси и, следовательно, не совпадает с плоскостью действия нагрузки (на рисунке след действия изгибающего момента).
Пример 3. В частном случае, когда для бруса прямоугольного сечения силовая линия проходит по одной из диагоналей (рис. 10.3.),
tg=-(h/b)[(bh3/12)/(hb3)/12]=-h/b.
Таким образом, нулевая линия проходит по другой диагонали. Из примера видно, как отклоняются друг от друга указанные линии.
Получив положение нулевой линии (N-N), находим наиболее напряжённые точки, как наиболее удалённые от неё. Подставим в формулу (10.1) координаты этих точек и учтем, что Mx=McosMy=Msin. Тогда условие прочности получит вид:
(10.4)
где х и у – координаты точки, наиболее удалённой от нейтральной линии (оси).
Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр) формула (10.4) упрощается
(10.5) Условие прочности для таких сечений примет вид:
(10.6)При подборе сечений приходится задаваться отношением Wx/Wy и,
зная [], Mmax и угол , путём последовательных попыток искать значения Wx и Wy, удовлетворяющие условию прочности (10.6).
10.2.1.2. Прогибы при косом изгибе.
Разложим силу F (рис. 10.4), на составляющие Fxи Fy.
Найдём отдельно прогибы от этих составляющих. Обозначив прогибы конца консоли длиной l по направлению осей х и у через fx и fy имеем:
Суммарный прогиб можно найти как геометрическую сумму:
Найдём теперь направление суммарного перемещения. Для этого определим значение угла наклона этого перемещения к вертикали: .Таким образом,
.Полученная формула идентична с формулой (10.3). Это позволяет сделать заключение, что | | ||
Следовательно (рис. 10.5), направление прогибов f перпендикулярно нулевой линии (N-N).
Вместе с тем отсюда вытекает важное условие, что направление прогибов не совпадает с направлением действующей силы.
В случаях действия пространственной системы сил ось изогнутого стержня представляет собой пространственную кривую.
-
10.3. Внецентренное действие продольной силы
Такая задача очень часто встречается при расчете опор мостов, фундаментов под насосы и станки и т.д. Рассмотрим действие на стержень двух равных и противоположных сил
F (рис. 10.6), направленных по прямой АА, параллельной оси стержня CC. Расстояние точки А от центра тяжести сечения СА=е называется эксцентриситетом.
Сделаем параллельный перенос сил из точек А в центр тяжести сечения С.
С
илы, зачёркнутые один раз, вызовут осевое сжатие, а пары сил, зачёркнутые дважды, вызовут чистый изгиб моментами M0=Fe. Так как плоскость действия изгибающих пар СА может не совпадать ни с одной из главных плоскостей инерции стержня, то в общем случае имеет место комбинация продольного сжатия и чистого косого изгиба.
Так как при осевом сжатии и чистом изгибе напряжения во всех сечениях одинаковы, то проверку прочности можно провести для любого сечения,
хотя бы К-К.
-
10.3.1. Определение напряжений
Рассмотрим случай внецентренного сжатия массивной колонны. Предположим, что сжимающая сила F (см. рис. 10.7.) приложена в точке К, которая имеет координаты xF и yF, отсчитанные относительно главных центральных осей инерции.
От этой силы в произвольном сечении стержня (колонны), при параллельном переносе сил в центр тяжести сечения (точка С), возникают продольная сжимающая сила N = -F и два изгибающих момента, которые вызывают сжатие в точках, лежащих в первой четверти:
Mx=-FyF ;
My=-FxF .
Напряжение в произвольной точке М, лежащей в положительной четверти произвольного поперечного сечения, равно
. (10.7) По формуле (1) можно найти напряжение в любой точке сжатой колонны; для этого необходимо величины х и у брать с учётом знака.
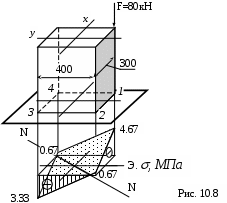
Пример. Определить напряжения и построить их эпюру в поперечном сечении колонны (см. рис. 11.8.).
Найдём изгибающие моменты:
Мх=80000 . 0.2=16000 Нм;
Му=80000 .0.15=12000 Нм.
Геометрические характеристики сечения:
площадь сечения
А=0.40.3=0.12 м2;
моменты сопротивления:
Wx=0.3(0.4)2/6=0.008 м3;
Wy=0.4(0.3)2/6=0.006 м3.
Найдём напряжения в четырех угловых точках поперечного сечения:
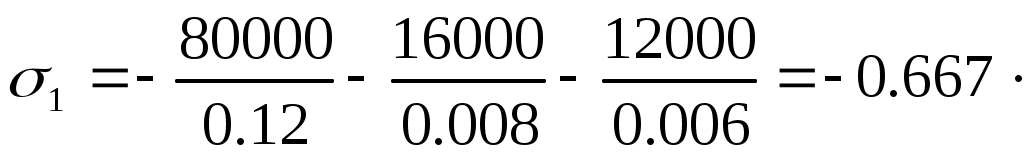106-2-2. Па-220. Па
3223.33 Па
4+2-20. Па.
По этим значениям построена эпюра напряжений.
10.3.2. Определение положения нулевой линии
Для того чтобы определить положение нулевой линии, преобразуем формулу (10.7). Подставим в эту формулу значение моментов, получим
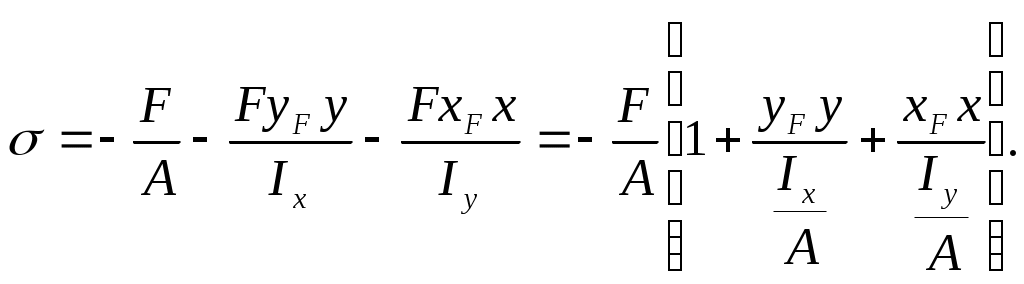
Величины, стоящие в знаменателе второго и третьего слагаемых, представляют собой квадраты радиусов инерции сечения, т.е.
Следовательно,
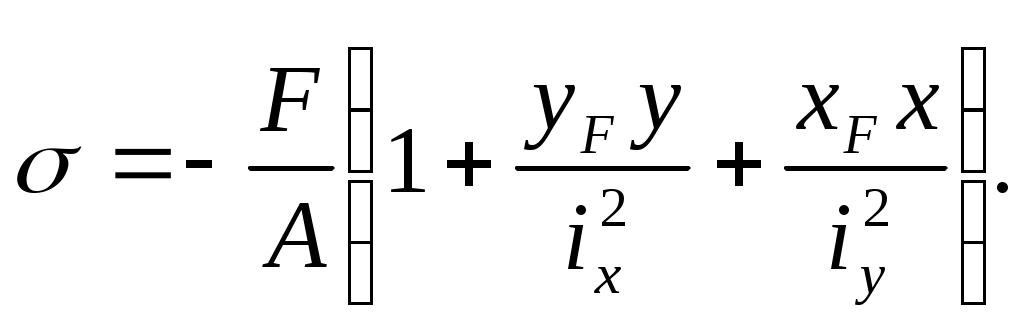(10.8) 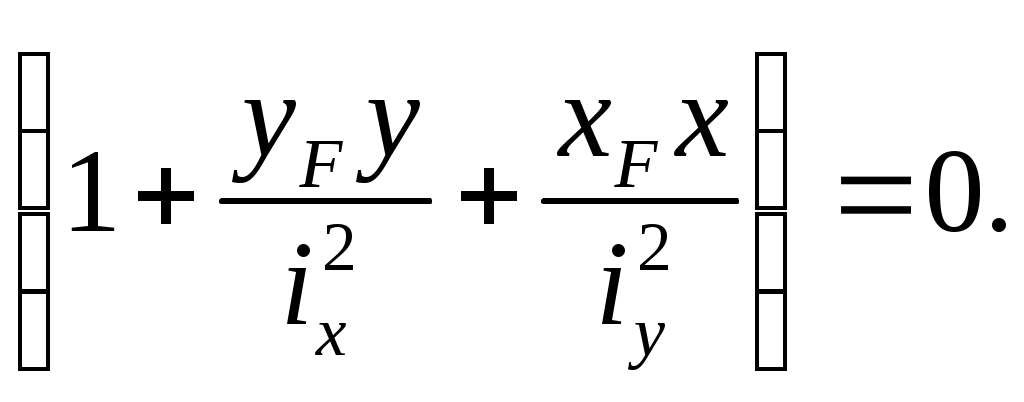Этой формулой, так же как и формулой (10.7), можно пользоваться для определения напряжений в любой точке поперечного сечения колонны. Обозначим координаты любой точки нулевой линии xN и yN . Если эти координаты поставить в уравнение (10.8) и учесть, что напряжения в нулевых точках равны нулю, то после сокращения на величину F/A получим уравнение нулевой линии (10.9)По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат.
О
бозначим эти отрезки через ах и ау (см. рис. 10.9) .Если положить xN=0, yN=ау, то из уравнения (10.9) получим
Точно так же для yN=0, xN=ax имеем
Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на осях координат:
(10.10)
Можно решить обратную задачу, выразив координаты точки приложения силы F при заданных отрезках, отсекаемых нулевой линией на осях координат:
(10.11) Отметим зависимость величин xF и ax , а также yF иay. Если силу приложить в точке с координатами ах и ау, то нулевая линия отсечёт отрезки на осях координат, равные соответственно xF и yF. Если сила приложена в т.1(рис. 10.10), а соответствующая нулевая линия I-I, то при силе в т.2, нулевая линия займёт положение II-II.
Рассмотрим некоторые характерные особенности, связанные с поведением нулевой линии при различных положениях силы F.
Если сила F приложена в точке, лежащей на оси Су (рис.10.11,а), то
нулевая линия отсекает на оси Сх отрезок, равный бесконечности:
Это означает, что нулевая линия будет параллельна оси Сх.
Представим себе, что сила F перемещается по оси Сх от центра тяжести С к краю сечения. В этом случае нулевая линия перемещается из бесконечности по направлению к сечению, оставаясь при этом всё время параллельной оси Су. Точно как же если сила перемещается по оси Су, то нулевая линия перемещается поступательно, оставаясь всё время параллельной оси Сх.
Так, например, когда сила последовательно приложена в точках 1, 2, 3, 4,
(рис. 11.11, а)), нулевая линия соответственно занимает положения I-I, II-II, III-III и т.д.
Рассмотрим случай, когда сила F перемещается по некоторой прямой СЕ, проходящей через центр тяжести сечения, но не совпадающей ни с одной из главных осей инерции. В этом случае нулевая линия будет также перемещаться параллельно самой себе. В самом деле, из отношения
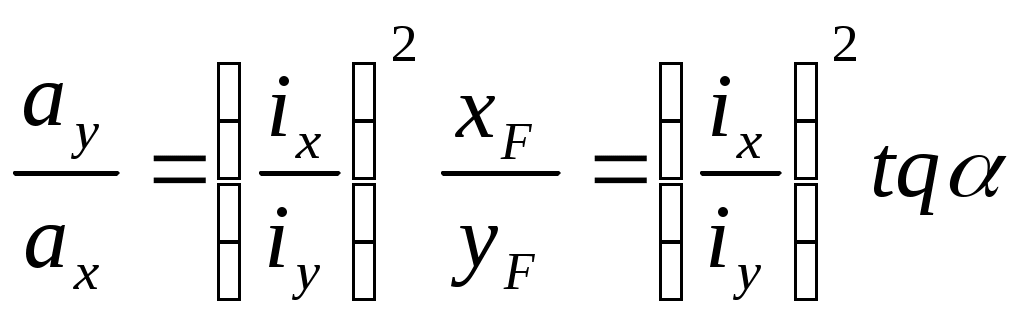
можно сделать вывод, что тангенс угла наклона нулевой линии ау /ax не зависит от численного значения координат точки приложения силы, а зависит от их отношения.
Рассмотрим случай, когда сила F перемещается по некоторой прямой