Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 412
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
(3.31)
Обычно:
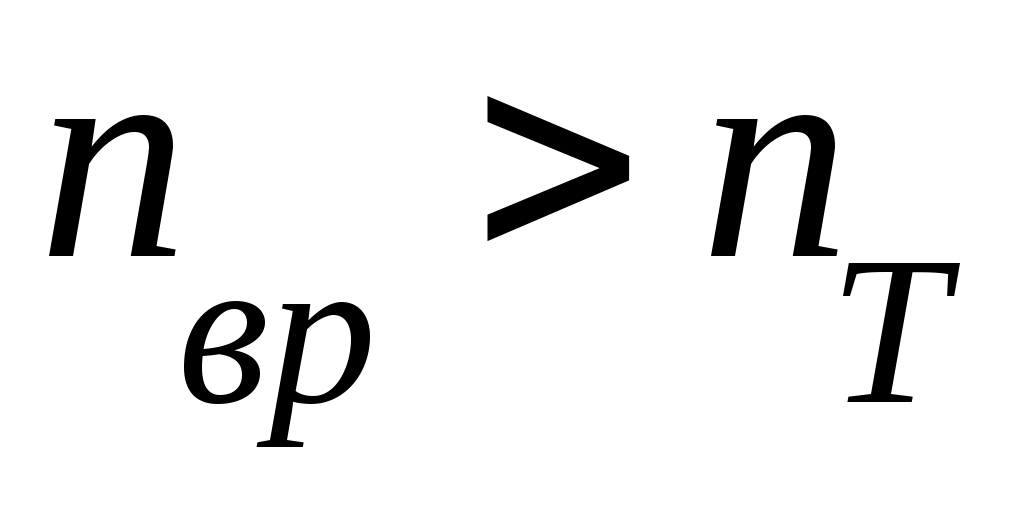 . (3.32)
. (3.32)
3.6.1. Условие прочности и три основных задачи сопротивления материалов
При расчете по допускаемым напряжениям при растяжении (сжатии) условие прочности записывается следующим образом:
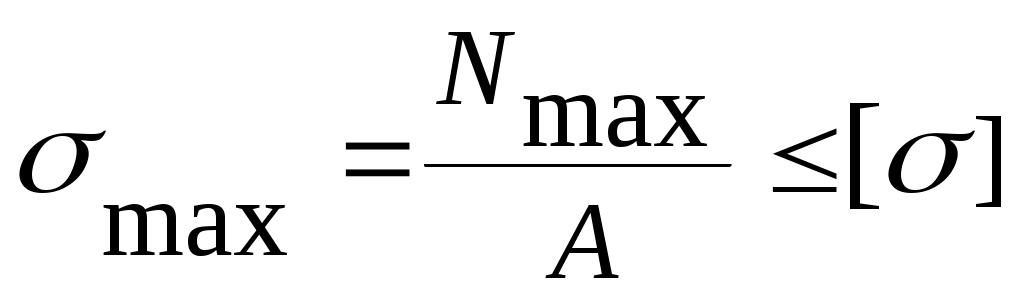 (3.33)
(3.33)
Исходя из условия прочности (3.33) можно рассмотреть три задачи, которые называются тремя основными задачами сопротивления материалов.
Известно допускаемое напряжение . Известны нагрузка и геометрические размеры конструкции. Определяют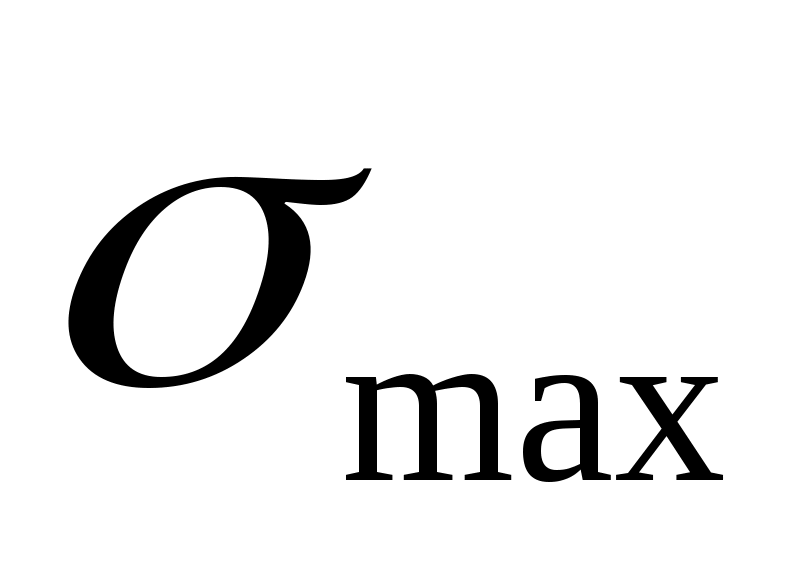 и проверяют выполнение условия (3.33).
и проверяют выполнение условия (3.33).
2.Задача подбора сечения
По известной нагрузке и допускаемому напряжению материала из (3.33) определяют(А) для наиболее напряженного элемента конструкции:
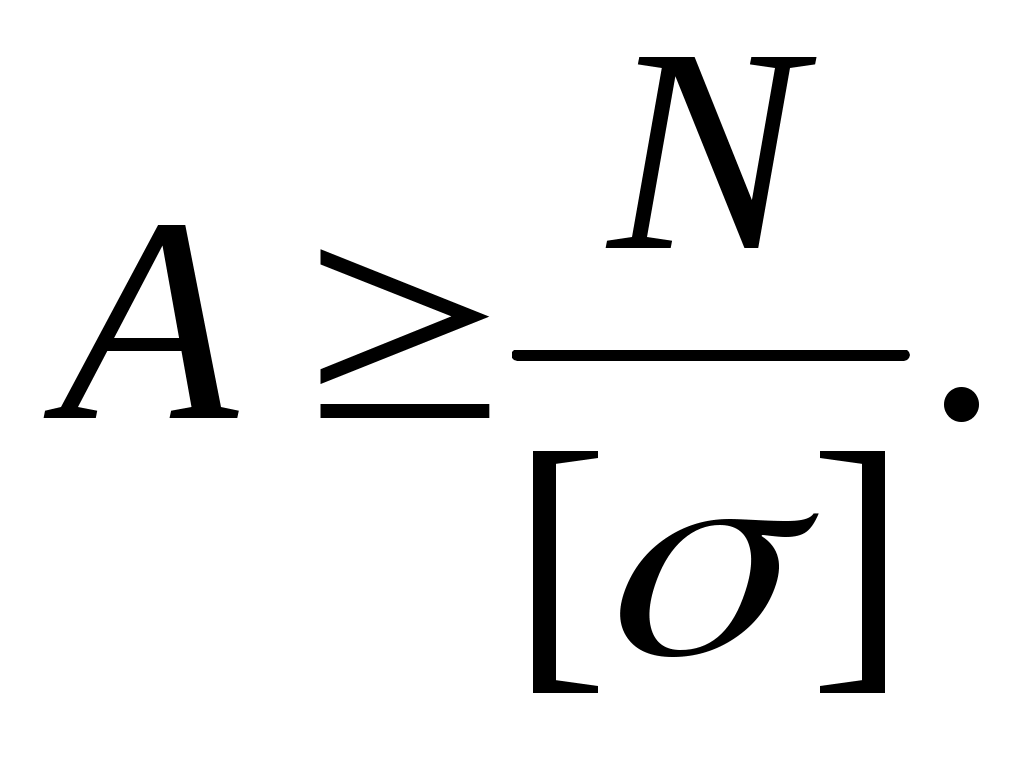
3.Задача определения допускаемой нагрузки
По известной площади и допускаемому напряжению материала наиболее напряженного элемента конструкции из условия (3.33), определяют допускаемое значение продольной силы(N).
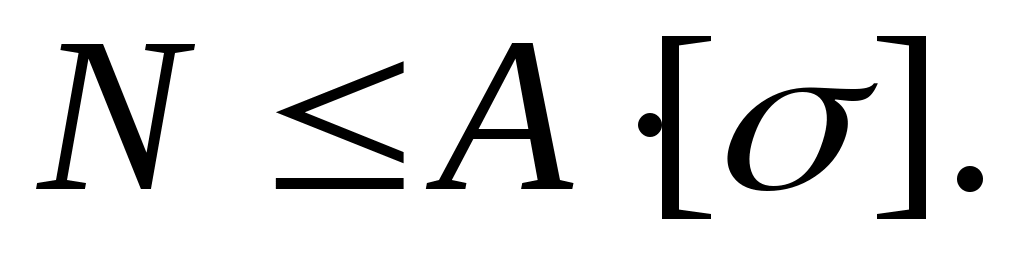
Зная (N), определяют допускаемое значение параметра внешней нагрузки.
ПРИМЕЧАНИЕ
При решении этих задач в неравенстве (3.33) допускается отклонение в пределах 5%.
3.6.2. Условие жёсткости и три основных задачи сопротивления материалов
Выполнение условии (3.33), ограничивающих величину напряжений, недостаточно для обеспечения нормальной работы конструкции. Наряду с условием прочности должно выполнятся условие жёсткости, ограничивающее величину перемещения (деформации).
Условие жесткости при растяжении (сжатии) прямого бруса может быть записано следующим образом:
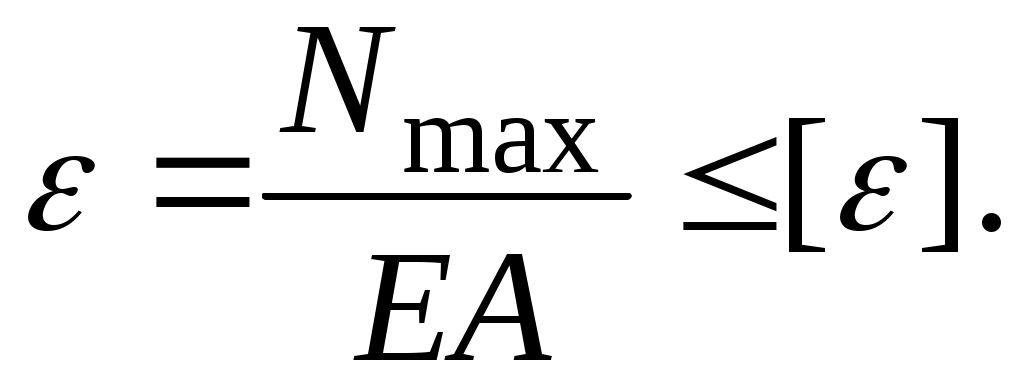 (3.34)
(3.34)
Из условия (3.34) можно решить три задачи, как и из условия (3.33): проверочный расчёт, подбор сечения и определение допускаемой нагрузки.
Вопросы для самопроверки
4. Напряжённое и деформированное состояние в точке
4.1. 1. Понятие напряженного состояния в точке и его виды
Ранее были получены формулы
cos2 ( 2) sin2
для определения напряжений, действующих по сечениям, наклонным к оси растянутого или сжатого стержня. Из этих формул видно, что с изменением наклона площадки, проходящей через какую – либо точку, изменяются и действующие на ней нормальные и касательные напряжения. При этом было выяснено, что наибольшие нормальные напряжения имеют место в поперечных сечениях, а наибольшие касательные напряжения – в сечениях, проведённых под углом 450 к оси стержня. И так, с поворотом площадки меняются и напряжения. Совокупность напряжений, возникающих во множестве площадок, проходящих через рассматриваемую точку, называется напряжённым состоянием в точке.
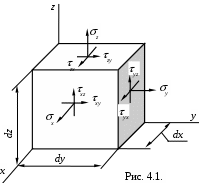
В общем случае при изучении напряжённого состояния в какой – либо точке К мысленно вырезают в окрестности этой точки параллелепипед со сторонами dx, dyи dz. Ввиду малости параллелепипеда можно считать, что напряжения на его гранях одинаковые. Если размеры параллелепипеда уменьшать, он будет стягиваться в точку и напряжения в соответствующих секущих плоскостях можно рассматривать как напряжения в исследуемой точке.
Напряжения, возникающие на трёх гранях элемента, показаны на рис. 4.1. На невидимых гранях элемента возникают соответственно такие же напряжения, но противоположного направления. На рис. 4.1. показано
объёмное напряжённое состояние в точке.
Е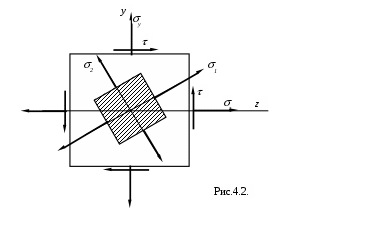
сли напряжения на любых площадках, проходящих через рассматриваемую точку, параллельны одной и той же плоскости, то имеет место плоско напряжённое состояние (рис. 4.2.).
Линейное напряженное состояние, например, испытывают точки бруса при центральном растяжении или сжатии .
Напряжения в наклонных площадках при
плоском напряженном состоянии
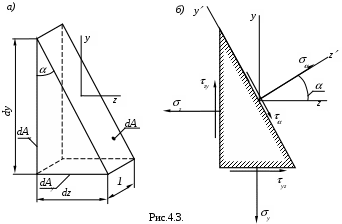
Рассмотрим, элементарный параллелепипед, разрезанный наклонным сечением, и изображенный в виде треугольной призмы (рис. 4.3.).
Из рис. 4.3,а следует, что
dAz=1dy=dAcos, dAy=1dz=dAsin. (4.1)
Напряжения на наклонной площадке и найдём из условий равновесия треугольной призмы.
Z=0; dA -z dAz cos -y dAz sin +zy dAz sin +yz dAy cos =0;
Y=0; dA+z dAz sin -y dAy cos +zy dAz cos -yz dAy sin.
Подставляя сюдазначения (4.1) и учтя, что zy=yz, а 2sincos = sin2 получим
=z cos2 +y sin2 -zy sin2; (4.2)
=0,5(z-y) sin2 +zy cos2. (4.3)
В ином виде формула (2) с учётом равенств cos2 =0,5(1+ cos2);
sin2 =0,5(1- cos2).
=0,5(z+y)+0,5(z-y) cos2 -zysin2. (4.2)
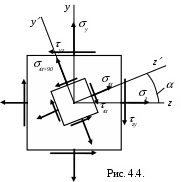
На рис. 4.4. наряду с исходным показан бесконечно малый элемент, выделенный в той же точке, но ориентированный по осям z,y. Найдём напряжения на гранях этого элемента.
Для определения у= +90 в выражение (4.2) вместо подставим + 900 , после чего получим
у=+90= 0,5(z+y)-0,5(z-y) cos2
+zy sin2. (4.4)
Касательные напряжения на площадках и +900 связаны законом парности, что в осях z,yозначает =zy= yz.
Сложим выражения(4.2) и (4.4). Как видим, сумма и +90не зависит от угла (инварианта к направлениям осей координат) и, следовательно, для данной точки эта сумма есть величина постоянная:
+ +90 =z+ y=const. (4.5)
Из формул (4.2) и (4.3) видно, что с изменением наклона площадки (рис. 4.4.), проходящей через какую – либо точку, изменяются и действующие на ней нормальные и касательные напряжения. Очевидно, что при каком –то угле 0 нормальное напряжение 0 достигнет наибольшего для данной точки значения.
На основании выражения (4.5) можно сделать вывод, что напряжения на перпендикулярной площадке будет наименьшим. Найдем эти площадки и экстремальные для точки нормальные напряжения. Для этого приравняем нулю производную
d /d =0.
Дифференцируя выражение (2) по аргументу получим
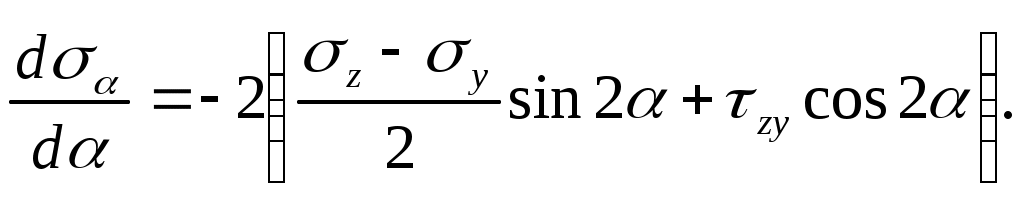 (4.6)
(4.6)
Очевидно, что выражение в скобках равно нулю. Если обозначить угол наклона искомых площадок через 0, то получим 0=0. Следовательно, на площадках, где действуют экстремальные для точки нормальные напряжения, касательные напряжения равны нулю. Такие площадки называются главными, а соответствующие им нормальные напряжения – главными напряжениями в точке.
Приравнивая выражение в скобках формулы (4.6) нулю, найдем тангенс двойного угла, определяющего наклон нормалей главных площадок:
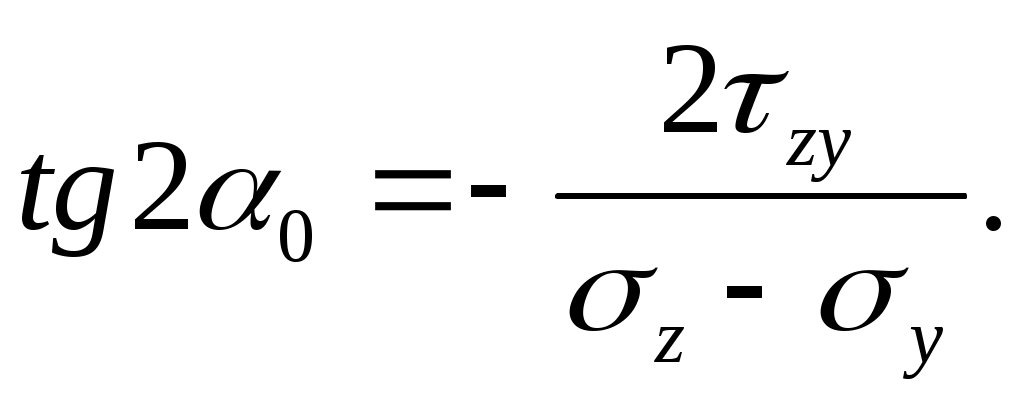 (4.7)
(4.7)
Выражение (7) дает два взаимно перпендикулярных направления с углами наклона 0 и 0 =
Обычно:
3.6.1. Условие прочности и три основных задачи сопротивления материалов
При расчете по допускаемым напряжениям при растяжении (сжатии) условие прочности записывается следующим образом:
Исходя из условия прочности (3.33) можно рассмотреть три задачи, которые называются тремя основными задачами сопротивления материалов.
-
Задача проверки прочности
Известно допускаемое напряжение . Известны нагрузка и геометрические размеры конструкции. Определяют
2.Задача подбора сечения
По известной нагрузке и допускаемому напряжению материала из (3.33) определяют(А) для наиболее напряженного элемента конструкции:
3.Задача определения допускаемой нагрузки
По известной площади и допускаемому напряжению материала наиболее напряженного элемента конструкции из условия (3.33), определяют допускаемое значение продольной силы(N).
Зная (N), определяют допускаемое значение параметра внешней нагрузки.
ПРИМЕЧАНИЕ
При решении этих задач в неравенстве (3.33) допускается отклонение в пределах 5%.
3.6.2. Условие жёсткости и три основных задачи сопротивления материалов
Выполнение условии (3.33), ограничивающих величину напряжений, недостаточно для обеспечения нормальной работы конструкции. Наряду с условием прочности должно выполнятся условие жёсткости, ограничивающее величину перемещения (деформации).
Условие жесткости при растяжении (сжатии) прямого бруса может быть записано следующим образом:
Из условия (3.34) можно решить три задачи, как и из условия (3.33): проверочный расчёт, подбор сечения и определение допускаемой нагрузки.
Вопросы для самопроверки
-
Какой вид деформации понимается под центральным растяжением (сжатием)? -
Как формулируется закон Гука для линейного напряженного состояния? -
Каковы напряжения в наклонных сечения бруса? -
Как формулируется закон парности касательных напряжений? -
По каким формулам вычисляются напряжения и деформации с учетом собственного веса? -
Как определяются относительная линейная деформация и абсолютное удлинение в брусе при сосредоточенных и распределенных осевых нагрузках? -
Какой коэффициент связывает относительные поперечную и продольную деформации? -
Как вычисляется работа внешних сил и потенциальная энергия при растяжении и сжатии? -
Что значит произвести расчет на прочность? На жесткость? -
Какие три основные задачи курса « Сопротивление материалов»? -
Что такое предел прочности? Допускаемое напряжение? Общий запас прочности?
-
Что такое предел пропорциональности? Текучести? -
Как определяется предел текучести при отсутствии площадки текучести? -
Какое явление называется наклепом? -
Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы? -
Можно ли определить модуль продольной упругости по диаграмме напряжений? -
Каков характер разрушения при сжатии образцов из чугуна, бетона? -
В каком направлении дерево обладает лучшими механическими свойствами?
4. Напряжённое и деформированное состояние в точке
4.1. 1. Понятие напряженного состояния в точке и его виды
Ранее были получены формулы
cos2 ( 2) sin2
для определения напряжений, действующих по сечениям, наклонным к оси растянутого или сжатого стержня. Из этих формул видно, что с изменением наклона площадки, проходящей через какую – либо точку, изменяются и действующие на ней нормальные и касательные напряжения. При этом было выяснено, что наибольшие нормальные напряжения имеют место в поперечных сечениях, а наибольшие касательные напряжения – в сечениях, проведённых под углом 450 к оси стержня. И так, с поворотом площадки меняются и напряжения. Совокупность напряжений, возникающих во множестве площадок, проходящих через рассматриваемую точку, называется напряжённым состоянием в точке.

В общем случае при изучении напряжённого состояния в какой – либо точке К мысленно вырезают в окрестности этой точки параллелепипед со сторонами dx, dyи dz. Ввиду малости параллелепипеда можно считать, что напряжения на его гранях одинаковые. Если размеры параллелепипеда уменьшать, он будет стягиваться в точку и напряжения в соответствующих секущих плоскостях можно рассматривать как напряжения в исследуемой точке.
Напряжения, возникающие на трёх гранях элемента, показаны на рис. 4.1. На невидимых гранях элемента возникают соответственно такие же напряжения, но противоположного направления. На рис. 4.1. показано
объёмное напряжённое состояние в точке.
Е

сли напряжения на любых площадках, проходящих через рассматриваемую точку, параллельны одной и той же плоскости, то имеет место плоско напряжённое состояние (рис. 4.2.).
Линейное напряженное состояние, например, испытывают точки бруса при центральном растяжении или сжатии .
- 1 2 3 4 5 6 7 8 9 ... 21
Напряжения в наклонных площадках при
плоском напряженном состоянии
Рассмотрим, элементарный параллелепипед, разрезанный наклонным сечением, и изображенный в виде треугольной призмы (рис. 4.3.).
Из рис. 4.3,а следует, что
dAz=1dy=dAcos, dAy=1dz=dAsin. (4.1)
Напряжения на наклонной площадке и найдём из условий равновесия треугольной призмы.
Z=0; dA -z dAz cos -y dAz sin +zy dAz sin +yz dAy cos =0;
Y=0; dA+z dAz sin -y dAy cos +zy dAz cos -yz dAy sin.
Подставляя сюдазначения (4.1) и учтя, что zy=yz, а 2sincos = sin2 получим
=z cos2 +y sin2 -zy sin2; (4.2)
=0,5(z-y) sin2 +zy cos2. (4.3)
В ином виде формула (2) с учётом равенств cos2 =0,5(1+ cos2);
sin2 =0,5(1- cos2).
=0,5(z+y)+0,5(z-y) cos2 -zysin2. (4.2)


На рис. 4.4. наряду с исходным показан бесконечно малый элемент, выделенный в той же точке, но ориентированный по осям z,y. Найдём напряжения на гранях этого элемента.
Для определения у= +90 в выражение (4.2) вместо подставим + 900 , после чего получим
у=+90= 0,5(z+y)-0,5(z-y) cos2
+zy sin2. (4.4)
Касательные напряжения на площадках и +900 связаны законом парности, что в осях z,yозначает =zy= yz.
Сложим выражения(4.2) и (4.4). Как видим, сумма и +90не зависит от угла (инварианта к направлениям осей координат) и, следовательно, для данной точки эта сумма есть величина постоянная:
+ +90 =z+ y=const. (4.5)
-
Главные напряжения
Из формул (4.2) и (4.3) видно, что с изменением наклона площадки (рис. 4.4.), проходящей через какую – либо точку, изменяются и действующие на ней нормальные и касательные напряжения. Очевидно, что при каком –то угле 0 нормальное напряжение 0 достигнет наибольшего для данной точки значения.
На основании выражения (4.5) можно сделать вывод, что напряжения на перпендикулярной площадке будет наименьшим. Найдем эти площадки и экстремальные для точки нормальные напряжения. Для этого приравняем нулю производную
d /d =0.
Дифференцируя выражение (2) по аргументу получим
Очевидно, что выражение в скобках равно нулю. Если обозначить угол наклона искомых площадок через 0, то получим 0=0. Следовательно, на площадках, где действуют экстремальные для точки нормальные напряжения, касательные напряжения равны нулю. Такие площадки называются главными, а соответствующие им нормальные напряжения – главными напряжениями в точке.
Приравнивая выражение в скобках формулы (4.6) нулю, найдем тангенс двойного угла, определяющего наклон нормалей главных площадок:
Выражение (7) дает два взаимно перпендикулярных направления с углами наклона 0 и 0 =