Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 289
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Имеем: D(jω) =1 + j2ω, U(ω) = 1, V(ω) = 2ω,
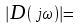
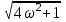 , tg φ = 2ω. Полагая V(ω) = 0, получаем начало годографа: |D(jω)| = 1. В пределах 0 ω∞ угол меняется от φ= 0 до φ= /2, т.е. вектор D(jω) поворачивается против часовой стрелки один раз на π/2. При этом, V(ω) растет, а U(ω) остается равным 1. Годограф получается в виде прямой, параллельной мнимой оси, рис. 5.5.
, tg φ = 2ω. Полагая V(ω) = 0, получаем начало годографа: |D(jω)| = 1. В пределах 0 ω∞ угол меняется от φ= 0 до φ= /2, т.е. вектор D(jω) поворачивается против часовой стрелки один раз на π/2. При этом, V(ω) растет, а U(ω) остается равным 1. Годограф получается в виде прямой, параллельной мнимой оси, рис. 5.5.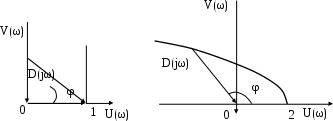
| Рис. 5.5. n = 1 | Рис. 5.6. n = 2 |
П

ример 5.7.
Выяснить устойчивость системы с характеристическим уравнением второй степени
9p2 + 4 p + 2 = 0.
Комплексный частотный полином, его действительное и мнимое слагаемые имеют вид:
D(jω) = – 9 ω2 + j4ω + 2,
U(ω) = 2 – 9 ω2,
V(ω) = 4 ω .
Полагая V(ω) = 0, находим: первая частота пересечения
 = 0. Годограф начинается в точке U(
= 0. Годограф начинается в точке U( ) = 2. Пересечение годографа с мнимой осью задается уравнением U(
) = 2. Пересечение годографа с мнимой осью задается уравнением U( ) = 0. Находим: вторая частота пересечения
) = 0. Находим: вторая частота пересечения  = 0,47. Ордината пересечения V(
= 0,47. Ордината пересечения V( ) 1,9. Во втором квадранте, с увеличением частоты, годограф уходит в бесконечность. График показан на рис. 5.6.
) 1,9. Во втором квадранте, с увеличением частоты, годограф уходит в бесконечность. График показан на рис. 5.6.Годограф проходит первый квадрант и уходит в бесконечность во втором. Вектор D(jω) поворачивается на угол, равный степени характеристического уравнения, умноженной на /2: Корни действительные, ω1 ω2 и требование последовательного возрастания частот пересечения выполняется. Следовательно, система устойчива.
П

ример 5.8.
Разомкнутая система имеет передаточную функцию
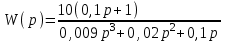 .
.Выяснить устойчивость замкнутой системы.
Характеристическое уравнение замкнутой системы
0,009p3 + 0,02p2 +1,1p + 10 = 0.
Комплексный частотный полином, нечетный и четный полиномы:
D(jω) = – j 0,009ω3 – j 1,1ω + 10 – 0,02 ω2,
V(ω) = 1,1ω – 0,009ω3,
U(ω) = 10 – 0,02 ω2.
Частоты пересечения:
V(ω) = 0,
 = 0,
= 0,  = 11,0.
= 11,0.U(ω) = 0,
 = 22,4.
= 22,4.Требование чередования частот при последовательном возрастании не выполняется:


 .
.Следовательно, система неустойчива.
Подтверждение этому получим, вычислив значения угла поворота вектора D(jω) при частотах пересечения с осями. Запишем тангенс аргумента:
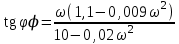 .
.Вычисляем:ω1 = 0, tg φ = 0, φ1 = 0.
ω2 = 22,4, tg φ = – ∞, φ2 = – 90.
ω3 = 11,0 tg φ = 0,00, φ3 = 0.
Угол φ не возрастает последовательно для каждой частоты пересечения. И не становится равным степени характеристического уравнения, умноженной на /2.
Как выглядит годограф Михайлова, показано на рис. 5.7.
Т
 аблица данных
аблица данных| ω | U | V |
| 0 | 10 | 0 |
| 5 | 9,5 | 4,4 |
| 11 | 7,6 | 0 |
| 15 | 5,5 | –14 |
| 22,4 | 0 | –76 |
Рис. 5.7. n = 3
Кривая не охватывает начала координат. Система неустойчивая.
П

ример 5.9.
Система с передаточной функцией
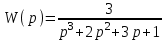
замыкается. Будет ли она устойчивой?
Находим передаточную функцию замкнутой системы
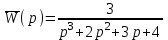 .
.Записываем характеристический
полином замкнутой системы
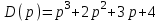
и соответствующий ему комплексный частотный полином
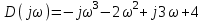 .
.Его действительная и мнимая части:
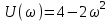 ,
, 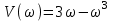 .
.Определяем частоты пересечения, координаты точек пересечения, углы.
V(ω) = 0.
 = 0, U(
= 0, U( ) = 4, φ(
) = 4, φ( ) = 0.
) = 0. =
= 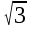 , (
, ( ) = –2, φ(
) = –2, φ( ) = 2 (/2).
) = 2 (/2).U(ω) = 0.
 =
= 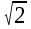 , V(
, V( ) =
) = 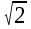 , φ(
, φ( ) = (/2).
) = (/2).ω = ∞ φ (ω) = – 3(/2).
Требование
 <
<  <
<  выполняется, углы последовательно возрастают, вектор D(jω) делает поворот на 3(/2) радиан.
выполняется, углы последовательно возрастают, вектор D(jω) делает поворот на 3(/2) радиан.Вывод: система устойчивая.
5.4. Критерий Найквиста
Критерий Гурвица и критерий Михайлова могут применяться для исследования устойчивости как разомкнутых, так и замкнутых систем, на основе характеристического полинома. Критерий Найквиста применяется для исследования устойчивости замкнутых систем. На основе комплексной частотной характеристики (амплитудно-фазовой частотной характеристики) разомкнутой системы.
КЧХ имеет действительное и мнимое слагаемые:
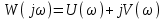 . (2.9)
. (2.9)Для построения КЧХ задают ω от 0 до ∞ и на комплексной плоскости получают годограф. Вид годографа, его расположение относительно точки – 1 на действительной оси, позволяют судить об устойчивости замкнутой системы.
Рассмотрим формулировки критерия Найквиста для трех случаев.
1. Разомкнутая система устойчива. Если годограф устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывает точку –1 на оси абсцисс, то замкнутая система будет устойчивой. Охватывает – замкнутая система неустойчивая.
Примеры годографов, соответствующих устойчивой и неустойчивой замкнутой системам, представлены на рис. 5.8 и 5.9.
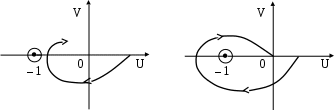
| Рис. 5.8. Устойчивость | Рис. 5.9. Неустойчивость |
Во второй формулировке критерия Найквиста используются понятие охвата точки годографом в положительном или отрицательном направлении. Положительным направлением считается такое, при котором конец вектора движется против часовой стрелки. Отрицательным – по часовой стрелке.
2. Разомкнутая система неустойчива. Если годограф неустойчивой разомкнутой системы при изменении ω от 0 до ∞ охватывает точку –1 на оси абсцисс в положительном направлении m/2 раз, где m – число корней характеристического уравнения разомкнутой системы с положительной действительной частью, то замкнутая система будет устойчивой.
Примеры годографов, соответствующих устойчивой и неустойчивой замкнутым системам во втором случае, представлены на рис. 5.10 и 5.11 для m = 2.
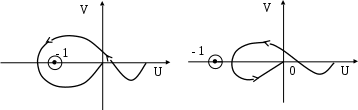
| Рис. 5.10. Устойчивость (m = 2) | 5.11. Неустойчивость (m= 2) |
Если разомкнутая система имеет передаточную функцию, содержащую в знаменателе множителем комплексную переменную р,
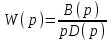 ,
,то комплексная частотная характеристика будет иметь неопределенность при ω = 0. Амплитуда становиться бесконечной. Годограф получается с бесконечной ветвью. Но если годограф мысленно дополнить зеркально отраженной ветвью и провести полуокружность бесконечно большого радиуса так, чтобы она пересекала положительную часть оси абсцисс, то такой прием позволяет использовать первую формулировку критерия Найквиста.
3. Разомкнутая система астатическая. Годограф зеркально отражается и кривые «замыкаются» на бесконечности. Тогда, если точка –1 на оси абсцисс оказалась вне замкнутой кривой – замкнутая система устойчивая. Если охватывается кривой – неустойчивая. Примеры таких годографов приведены на рис. 5.12 и 5.13.
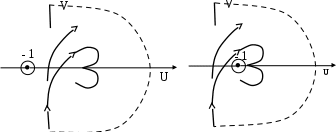
| Рис. 5.12. Устойчивость | Рис. 5.13. Неустойчивость |
Замкнутая система будет находиться на границе устойчивости, если годограф разомкнутой системы проходит через точку –1 оси абсцисс. Аналитически это условие можно записать в виде
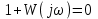 .
.Кривые Найквиста наглядно показывают влияние коэффициента усиления на устойчивость системы. У комплексной частотной характеристики, в которой коэффициент усиления увеличивают, размеры и положение годографа меняются относительно точки с координатами (–1,0). Допустим, имеется кривая 1, отвечающая границе устойчивости, рис.5.14. Предельный коэффициент усиления k= k. Кривая 2, для которой k k, отвечает устойчивой системе, кривая 3, для которойk k - неустойчивой. Увеличение коэффициента усиления вызывает смещение влево точки пересечения кривой 2 с отрицательной частью действительной оси. То есть, может перевести систему из устойчивого состояния в неустойчивое.

Рис. 5.14. Влияние коэффициентов усиления на расположение
кривых Найквиста:
1 k = k, 2 kk, 3 – k k
Система, имеющая годограф, изображенный на рис. 5.14, с увеличением коэффициента усиления способна реализовать два состояния: «устойчивость – неустойчивость». Для более сложных кривых число состояний может увеличиваться.
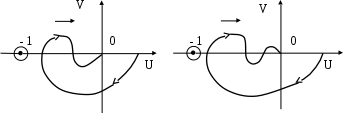
| Рис. 5.15. В системе возможны два перехода «устойчивость – неустойчивость» | Рис. 5.16. В системе возможны три перехода «устойчивость – неустойчивость» |
Например, у кривой с одним максимумом в отрицательной полуплоскости (рис. 5.15) по мере увеличения коэффициента усиления устойчивое состояние сменяется неустойчивым, а затем снова устойчивым. У кривой с двумя максимумами (рис.5.16), при увеличении коэффициента усиления, реализуются состояния: «устойчивость – неустойчивость – устойчивость – неустойчивость». Система может устойчиво работать в двух разных интервалах изменения коэффициента усиления. Это свойство не обнаруживается применением критерия Гурвица или Михайлова.