Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Коэффициент усиления на границе устойчивости рассчитывают, приравнивая комплексную частотную характеристику минус единице:

.






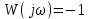Пример 5.10.

Дана передаточная функция разомкнутой системы:

.

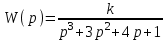Полагая k = 2 проверить с помощью критерия Найквиста, будет ли устойчивой замкнутая система?
Предварительно выясняем устойчивость разомкнутой системы по критерию Гурвица: система устойчива.

Найдем комплексную частотную характеристику разомкнутой системы:

.

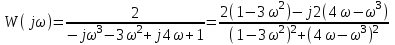Выделим действительный и мнимый частотные полиномы:

,

.

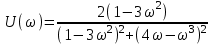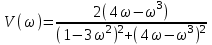Построим годограф разомкнутой системы.

По условию V(ω) = 0 находим частоты пересечения годографом действительной оси и соответствующие значения U(ω):

V(ω) = 0, 4ω – ω³ = 0, = 0, = 2,

U(0) = 2. U(2) = – 0,18.

Полагая U(ω) = 0, находим частоту пересечения годографом мнимой оси и соответствующее значение V(ω):

U(ω) = 0, 1 – 3ω² = 0, ,

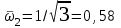V(0,58) = – 0,94.

Для ω = 1 получаем U(1) = – 0,3, V(1) = – 0,46.

При ω = ∞ U(∞) = 0, V(∞) = 0.

Вид годографа показан на рис. 5.17.

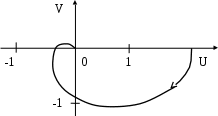
Рис. 5.17. Годограф по условиям примера 5.10
Разомкнутая система устойчивая, годограф не охватывает точку (–1,0), значит, замкнутая система тоже устойчивая.
П

ример 5.11.

Система на границе устойчивости имеет передаточную функцию

.

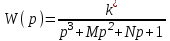Как зависит предельный коэффициент усиления k^ от параметров M и N?
Найдем комплексную частотную характеристику

.

На границе устойчивости

---

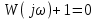
. Приравнивая по отдельности действительную и мнимую части этого уравнения, получаем:

,

.

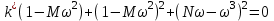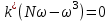Корни второго уравнения: 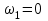и 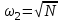. Границе отвечает ω₂.

Подставляя ω₂ в первое уравнение, получаем:

.

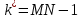В примере 5.10 М = 3, N= 4, k^* = 11. Для такого коэффициента усиления U(2) = – 1. То есть, годограф проходит через точку – 1 оси абсцисс.
П

ример 5.12.

Передаточная функция разомкнутой системы

.

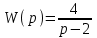Выяснить устойчивость замкнутой системы.
Проверка по критерию Гурвица показывает, что разомкнутая система неустойчивая.

Запишем частотные характеристики:

.

, .

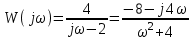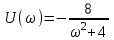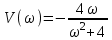Точек пересечения годографа с осью абсцисс две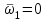: при и при = ∞.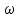

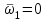,	U(0) = – 2,	V(0) = 0.
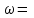∞,	U(∞) = 0,	V(∞) = 0.

Другие точки годографа уточняют вид кривой.

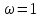,	U(1) = – 1,6,	V(1) = – 0,8.
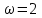,	U(2) = – 1,	V(2) = – 1.
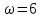,	U(6) = – 0,2,	V(6) = – 0,6.

---

Кривая располагается в третьем квадранте.

Годограф показан на рис. 5.18.

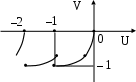
Рис. 5.18. Устойчивость дляm= 1
Годограф охватывает в положительном направлении точку – 1 наполовину, m/2 = 1/2 раз. Критерий Найквиста удовлетворяется – замкнутая система устойчивая.

Вывод подтверждается, если записать передаточную функцию замкнутой системы:

.

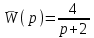По характеристическому полиному сразу видно, что корень отрицательный.

5.5. Выделение области

устойчивости D – разбиением

Устойчивость системы автоматического регулирования зависит от того, какими будут коэффициенты дифференциального уравнения, которое её описывает. Одна часть коэффициентов обеспечивает устойчивые решения дифференциального уравнения, другая часть – дополняющая первую - обеспечивает неустойчивые решения.
Идея метода D - разбиения заключается в том, чтобы найти границу между этими коэффициентами и тем самым указать область устойчивости. Для этого выделяют один или два важных коэффициента, изменяют их и исследуют, как меняются корни характеристического уравнения. Все остальные коэффициенты фиксируются.

Пусть дано характеристическое уравнение системы автоматического регулирования:

. (2.7.)

Пусть все коэффициенты заданы, кроме 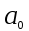и 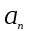. Предположим, что уравнение (2.7.) имеет в плоскости корней k корней слева от мнимой оси и n - k корней справа для каких–то значени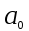й и 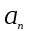, рис. 5.19.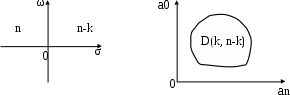

Рис. 5.19. Плоскость корней

Рис 5.20. Плоскость коэффициентов

Будем менять значения коэффициентов 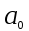и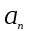

---

и находить корни. Возможно, для некоторой совокупности значений и количество корней слева и справа от мнимой оси не меняется. Т. е. соотношение между k и n-k остается постоянным. Тогда как совокупность других значений коэффициентов и меняет соотношение между k и n–k. Можно указать границу, отделяющую область постоянного отношения k и  n–k. Эту область обозначают D(k, n–k), рис. 5.20.

Например, для характеристического уравнения четвертой степени



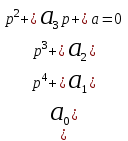
в плоскости коэффициентов могут быть следующие области:

D(0,4), D(1,3), D(2,2), D(3,1), D(4,0).

Всего n+ 1 областей.

Из всех D(k, n–k) областью устойчивости будет только одна: D(n, 0). В ней все корни, располагающиеся слева от мнимой оси, имеют отрицательную действительную часть. Мнимая ось – граница устойчивости в плоскости корней. В плоскости коэффициентов кривая, отделяющая область устойчивости от области неустойчивости, будет ничем иным, как преобразованной мнимой осью.
5.5.1. D – разбиение по одному параметру
Изучение метода D - разбиения начнем с выяснения влияния на устойчивость одного параметра. При заданных значениях других параметров. Обозначим параметр символом λ. Это может быть коэффициент характеристического уравнения, или сочетание коэффициентов. Например, в уравнении



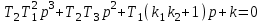
можно назвать параметром .

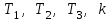Допустим, сделан выбор 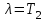. Тогда уравнение примет вид

.

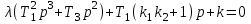Полином, который умножается на λ, обозначим Q(p), остальную часть S(p). Уравнение примет общий вид:

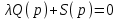. (5.4)

Представив уравнение (5.4) в виде

---

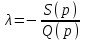, (5.5)

получаем λ как функцию переменной p.

Чтобы построить границы области устойчивости, полагаем

p= jω. Тогда λ (p) становится комплексным числом:

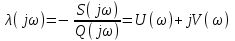. (5.6)

Если теперь задавать ω от 0 до + ∞, вектор λ (jω) вычертит некоторую кривую на комплексной плоскости (U, V). Эта кривая отображает на плоскость U, Vмнимую ось комплексной плоскости корней, то есть будет границей, по одну сторону которой k корней, по другую n– k.
Если задавать ω от 0 до – ∞, получится зеркальное отображение кривой для + ω. Поэтому кривую рассчитывают для положительных ω, а затем дополняют зеркальным отображением относительно действительной оси.

Чтобы разобраться, по какую сторону находятся k корней, область D - разбиения выделяется штриховкой. Соображения следующие.

При движении по мнимой оси в плоскости корней (рис. 5.21) от ω = – ∞ до ω = + ∞ та область, в которой находятся все корни устойчивости будет все время слева. Она показана штриховкой.

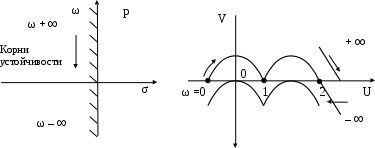
Рис. 5.21. Плоскость корней

Рис. 5.22. Кривые D-разбиения со штриховкой

Требуется, чтобы и в плоскости (U, V) область устойчивости находилась слева от кривой D-разбиения, если двигаться от – ∞ к + ∞. Левая сторона кривой штрихуется.
Рассмотрим в качестве примера кривую, изображенную на рисунке 5.22. На этой кривой показано, как надо наносить штриховку. Область устойчивости ограничена кривой со штриховкой внутрь.

Параметр λ по физическому смыслу есть величина действительная, поэтому для расчетов используется только отрезок действительной оси, охваченной кривыми со штриховкой внутрь: от точки 1 до точки 2 на рис. 5.22.

П

ример 5.13

Дано характеристическое уравнение:

.

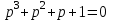Пусть параметром будет λ, одно из значений которого λ=1 проставлено в уравнении. Надо найти, в каком интервале изменений λ характеристическое уравнение отвечает устойчивой системе автоматического регулирования.

---