Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx

Объединив выходные сигналы посредством сумматора (на рис. 4.7 показано штриховыми линиями), получим: 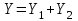. То есть,

.

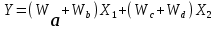Передаточная функция для сигнала X₁

,

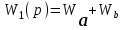для сигнала X₂

.

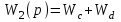Один из сигналов может быть управляющим, другой - возмущением.

4.3. Статические и астатические

системы
Система, в структуре которой нет последовательно присоединенного интегрирующего звена, называется статической. Примером может служить последовательное соединение звеньев с передаточными функциями

, , .

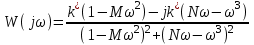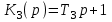Передаточная функция системы имеет вид

.

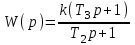Система, в структуре которой есть последовательно присоединенное интегрирующее звено, называется астатической.

Если к трем предыдущим присоединить последовательно интегрирующее звено с передаточной функцией k₁/T₁p, получится передаточная функция

.

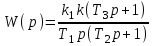В знаменателе появился множитель: комплексная переменная p. Последовательное присоединение еще одного интегрирующего звена даст множитель p². Говорят, в первом случае система обладает астатизмом первой степени, во втором – второй степени. В общем случае – астатизмом степени n.

Т.о. по тому, нет или есть в знаменателе передаточной функции множитель pⁿ, системы делятся на два класса: статические и астатические.

В статической системе при постоянном входном воздействии выходная величина со временем становится постоянной, принимая значение, отличное от первоначального.

В астатической системе при постоянном входном воздействии выходная величина непрерывно изменяется.
П

ример 4.10.

Наиболее простым астатическим звеном является интегрирующее

---

, у которого .

Показать, что при постоянном входном воздействии выходная величина должна неограниченно возрастать.
Записываем операторное уравнение

,

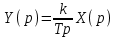вводим условие ступенчатого воздействия 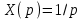и получаем изображение переходной функции

.

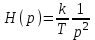В таблице изображений по Лапласу дроби 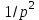соответствует оригинал t. Значит, переходной функцией будет

.

Зависимость линейная, при t 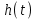 ∞ неограниченно возрастает.
П

ример 4.11.

Можно ли получить астатическую систему, охватив интегрирующее звено жесткой обратной связью?
Записывая передаточные функции звеньев в виде

и

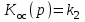
получаем передаточную функцию замкнутой системы

.

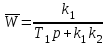Вводя новые постоянные: 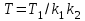и 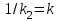убеждаемся, что система имеет свойства инерционного звена:

.

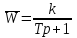То есть, система статическая. Однако, нетрудно убедиться, что при мягкой обратной связи система будет астатической.

4.4. Перестановка структурных

элементов
Структура системы, обеспечивающая заданную передаточную функцию, не есть нечто неизмененное. Одной и той же передаточной функции могут соответствовать разные структуры. Возможен переход от одной к другой, но при этом должны выполняться определенные требования. Например, включение дополнительного сумматора или дополнительного звена и др. Требования порождаются изменением направления передачи сигналов в системе при перестановке элементов.

Конкретная задача формулируется так. Дана исходная структура системы, обозначены входные и выходные сигналы. Требуется изменить структуру, переставив местами звенья при условии, что передаточная функция системы останется неизменной. То есть, остаются прежними входные и выходные сигналы системы.

---

4.4.1. Перестановка узлов и сумматоров

4.4.1.1. Перенос узла через узел
Рассматривается система из двух узлов, рис. 4.8.

На входе в систему сигнал Х₁, на выходе - тоже. Перестановка узлов не меняет входной и выходной сигналы.

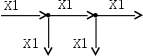
Рис. 4.8. Система из двух узлов

4.4.1.2. Перенос сумматора через сумматор
Исходная система состоит из двух сумматоров, рис.4.9 а. На входе сигнал Х₁, на выходе Х₆. После перестановки сумматоров сигнал на входе и сигнал на выходе должны оставаться теми же, рис. 4.9 б.

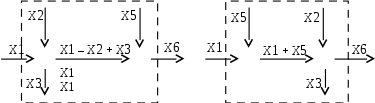
Рис. 4.9 а. Система до перестановки

Рис. 4.9 б. Система после перестановки

Легко убедиться, что это так: сигнал Х₆ = Х₁  Х₂ + Х₃ + Х₅ как до, так и после перестановки. Меняется сигнал от сумматора к сумматору.

Вывод: перенос сумматора через сумматор оставляет выходной сигнал прежним.

4.4.1.3. Перенос сумматора через узел по направлению

передачи сигнала
Исходная схема, рис. 4.10 а, содержит два входа, Х₁ и Х₂, и два выхода Х₃ и Х₃. Следовательно, на эквивалентной схеме, рис. 4.10 б, должны быть те же два входа и те же два выхода. Сигналы связаны между собой равенством Х₃ = Х₁ + Х₂, которое является условием формирования сигнала Х₃.

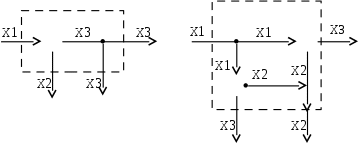
Рис. 4.10 а. Система до перестановки

Рис. 4.10 б. Эквивалентная структурная схема

После переноса сумматора входной сигнал Х₁ подается на узел и от него на сумматор. Входной сигнал Х₂ подается на сумматор, складывается с сигналом Х₁ и формирует выходной сигнал Х₃. Но, по условию, должен быть еще один выходной сигнал Х₃, который обязан быть суммой Х₁ + Х₂. Поэтому на пути сигнала Х₁, направленного на выход, следует поставить дополнительный сумматор, к которому подвести сигнал

---

Х₂. Такой сигнал можно получить, поставив дополнительно узел на пути входного сигнала Х₂. Получается эквивалентная схема, которая показана на рис. 4.10 б. На ней те же два входных и два выходных сигнала, что и на исходной схеме.

Вывод: перенос сумматора через узел по направлению передачи сигнала, при условии сохранения входных и выходных сигналов системы, требует включения второго сумматора в то ответвление от узла, которое направляет сигнал на выход. При этом должны быть соблюдены условия формирования выходного сигнала от сумматора.

4.4.1.4. Перенос сумматора через узел против направления передачи сигнала
Исходная схема имеет два входа, Х₁ и Х₂ и два выхода, Х₁ и Х₃, рис. 4.11 а. Эквивалентная схема должна иметь те же входы и выходы. Сигналы связаны между собой равенством Х₃ = Х₁ + Х₂.

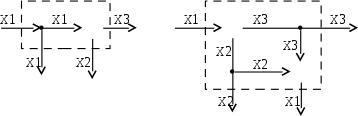
Рис. 4.11 а. Система до перестановки

Рис. 4.11 б. Эквивалентная структурная схема

После перестановки входные сигналы Х₁ и Х₂ посредством сумматора формируют сигнал Х₃, который разветвляется узлом на два выходных, рис 4.11 б. Один из них, по условию, остается самим собой. Второй Х₃ должен выйти из системы сигналом Х₁. При этом сигнал Х₁ надо получить из сигнала Х₃ по условию: Х₃ = Х₁ + Х₂, т.к. других сигналов в системе нет. Очевидно, Х₁ = Х₃  Х₂. Реализовать вычитание можно посредством сумматора, в котором сигнал Х₂ преобразуется в отрицательный перед сложением с сигналом Х₃. Для передачи сигнала Х₂ на сумматор надо на пути входного сигнала Х₂ поставить узел. Эквивалентная схема получается такой, как на рис. 4.11 б.

Вывод: перенос сумматора через узел против направления передачи сигнала, при условии сохранения входных и выходных сигналов системы, требует включения корректирующего сумматора на пути одного из ответвляющихся после узла сигналов. К корретирующему сумматору подводится второй входной сигнал Х₂ с обратным знаком.

4.4.2. Перенос узла или сумматора через звено

---

4.4.2.1. Перенос узла с выхода звена на вход
Исходная схема имеет один входной сигнал Х₁ и два выходных сигнала, Х₂ и Х₂, рис. 4.12 а. Сигнал Х₂ получается преобразованием сигнала Х₁ по закону Х₂ = K Х₁ , где K – передаточная функция звена.

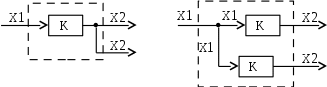
Рис. 4.12 а. Система до перестановки

Рис. 4.12 б. Эквивалентная структурная схема

После переноса в эквивалентной схеме один из выходных сигналов X₂ получается, как прежде. Второй надо получить, преобразуя ответвляющийся от узла сигнал Х₁. То есть, поставить на линии ответвления звено с передаточной функцией K такой же, как у исходного звена.

Вывод: перенос узла с выхода звена на вход требует включения второго такого звена в ответвление от узла.

4.4.2.2. Перенос узла с входа звена на выход
Исходная схема имеет один входной сигнал Х₁ и два выходных сигнала, Х₁ и Х₂, рис. 4.13 а. Условием формирования сигнала Х₂ является равенство Х₂ = K Х₁. После переноса, эквивалентная схема должна иметь тот же входной сигнал Х₁ и те же выходные сигналы, Х₁ и Х₂. Однако, от узла ответвляется на выход сигнал Х₂, который надо преобразовать в сигнал Х₁. По условию Х₂ = KХ₁ это можно сделать так: Х₁ = (1/K) Х₂. Т.е. включитьв линию звено с передаточной функцией, обратной заданной. Что и показано на рис. 4.13 б.

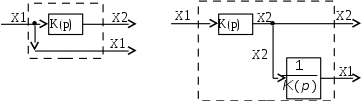
Рис. 4.13 а. Система до перестановки

Рис. 4.13 б. Эквивалентная система после перестановки

Перенос узла с входа звена на выход, при условии сохранения входного и выходного сигналов системы, требует включения в линию выхода звена с передаточной функцией, обратной заданной.

4.4.2.3. Перенос сумматора с выхода звена на вход
Исходная схема имеет два входных сигнала Х₁ и Х₃, и один выходной сигнал Х₄, рис. 4.14 а. Выходной сигнал формируется по уравнению Х₄ = Х₂ + Х₃ = K Х

---