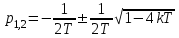Файл: Федеральное агенство по образованию рф казанский государственный энергетический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 288
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 + Х3, которое является операторным уравнением исходной системы. После переноса эквивалентная схема должна иметь те же входные сигналы Х1 и Х3, и тот же выходной сигнал Х4, рис. 4.14 б.
На исходной схеме с выхода звена уходит сигнал Х2. На эквивалентной схеме с выхода этого звена должен уходить сигнал Х4. Такое возможно, если входным сигналом будет не Х1, а какой-то другой, Y2. В свою очередь Y2 обязан быть суммой Х1 и сигнала Y1, который будет преобразованием входного сигнала Х3 корректирующим звеном с передаточной функцией Kк. Передаточную функцию Kк требуется определить. Выразим эти умозаключения операторным уравнением
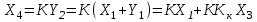
Так как сигнал Х4тот же, что и в исходном операторном уравнении, должно выполняться равенство
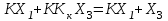
Из него следует, что корректирующим звеном в линии сигнала Х3 будет Kк = 1/K. Что и изображено на схеме рис. 4.14 б.
Вывод: перенос сумматора с выхода звена на вход, при условии сохранения входных и выходного сигналов системы, требует включения в линию второго подаваемого на сумматор сигнала звена с передаточной функцией, обратной заданной.
4.4.2.4. Перенос сумматора с входа звена на выход
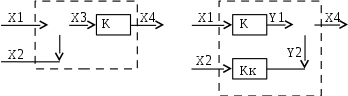
Исходная схема имеет два входных сигнала Х1 и Х2 и один выходной сигнал Х4, рис. 4.15 а. Выходной сигнал связан с входными уравнением Х4 = KХ3 = K Х1 + K Х2. Эквивалентная схема должна иметь те же входные и выходной сигналы.
Чтобы в эквивалентной схеме получить тот же сигнал Х4, в линию входного сигнала Х2 следует ввести корректирующее звено с передаточной функцией Kк. Тогда сигнал Х4 окажется связанным с входными сигналами уравнением:
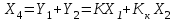
Сравнивая его с исходным уравнением Х4 = K Х1 + KХ2, приходим к заключению, что корректирующая передаточная функция Kк= K. Что и обозначено на схеме рис. 4.15 б.
Вывод: перенос сумматора с входа звена на выход, при условии сохранения входных и выходных сигналов системы, требует включения в линию второго подаваемого на сумматор сигнала звена, с передаточной функцией, одинаковой с заданной.
П
ример 4.10.
Найти передаточную функцию системы, структурная схема которой изображена на рис. 4.16.
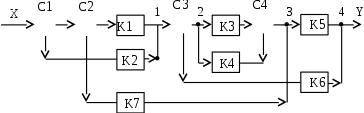
Рис. 4.16. Исходная структурная схема
Звенья с передаточными функциями K3 и K4 соединены параллельно. Сделаем первое упрощение схемы, заменив их передаточной функцией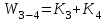
. Из схемы устраняются узел 2 и сумматор С4. Также переставим сумматоры С1 и С2. Схема примет вид:
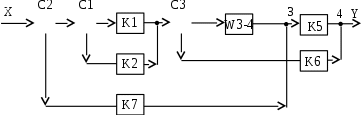
Обнаруживаем, что звено с передаточной функцией K1 охвачено положительной обратной связью через звено с передаточной функцией K2. Схема упрощается, если ввести передаточную функцию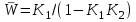
. Сумматор С1 и узел 1 устраняются. Остается:
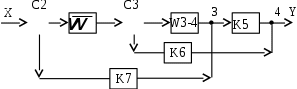
Дальнейшее упрощение схемы связано с переносом узла 4 с выхода звена K5 на его вход и перестановкой с узлом 3. В ответвлении от узла 4 появляется звено K5, последовательно включенное со звеном K6.
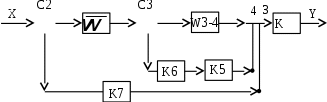
Обнаруживается замкнутый контур из звеньев с передаточными функциями W3-4, K5 и K6. Его можно заменить звеном с передаточной функцией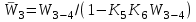
. Сумматор С3 и узел 4 устраняются. Схема приобретает вид:
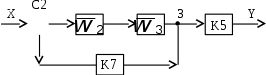
Выражая последний замкнутый контур звеном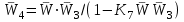
, приходим к схеме
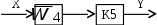
Следовательно, передаточная функция системы, имеющей структурную схему, показанную на рис. 4.16, есть
,
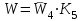или, в развернутом виде,
.
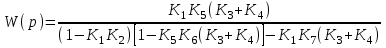Литература
1. Бесекерский В.А., Попов Е.П. Теория автоматического управления. – СПб , изд-во «Профессия» , 2004. – 752 с.
2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
3. Макаров И.М., Менский Б.М. Линейные автоматические системы. – М.: Машиностроение, 1947. – 464 с.
4. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.: Машиностроение, 1973. – 606 с.
5.1. Понятие об устойчивости
Система, которая после завершения переходного процесса приходит к состоянию установившегося равновесия, называется устойчивой. В устойчивой системе регулируемая величина со временем стремится к постоянному значению.
Система называется неустойчивой, если после устранения воздействия она удаляется от состояния равновесия или совершает около него недопустимо большие колебания. В неустойчивой системе регулируемая величина со временем возрастает.
Если заранее выяснить, будет ли регулируемая величина неограниченно возрастать после воздействия, можно получить ответ на вопрос об устойчивости системы.
Характер воздействия на систему и поведение управляемой величины описывается дифференциальным уравнением. Оно было записано для разомкнутой системы в главе 2:
(2.1)
Когда воздействие на систему прекращается, правая часть обращается в ноль и дальнейшее изменение управляемой величины описывается однородным дифференциальным уравнением
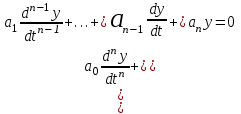. (5.1)
Решение однородного уравнения показывает, возрастает или не возрастает со временем управляемая величина. Решение ищут, полагая y(t) = ept. Беря производные и подставляя в уравнение (5.1) находят характеристическое уравнение
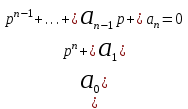(2.7)
решая которое, получают корни pi. Полное решение уравнения (5.1) слагается из экспонент:
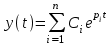(5.2)
где Сi – постоянные интегрирования.
Функция y(t) – описывает переходной процесс; он полностью определяется значением корней pi.
Корни характеристического уравнения могут быть действительными, комплексными, мнимыми. Если корни действительные и отрицательные, каждая экспонента со временем стремится к нулю, следовательно, y(t) 0. По окончании переходного процесса система приходит к состоянию установившегося равновесия.
Если корни действительные и положительные, все экспоненты со временем неограниченно возрастают, y(t) ∞. Процесс неустойчивый, система удаляется от состояния равновесия.
Если корни комплексно-сопряженные с отрицательной действительной частью, каждая экспонента со временем стремится к нулю, имея колебательную составляющую. И в этом случае y(t) 0. Система, следовательно, устойчивая.
В случае комплексно-сопряженных корней с положительной действительной частьюсистема неустойчивая.
При наличии чисто мнимых корней выходная величина совершает гармонические колебания. Мнимые корни соответствуют границе устойчивости.
Итак, система устойчива только в том случае, когда действительная часть корней характеристического уравнения отрицательная.
Для суждения об устойчивости необязательно решать дифференциальное уравнение. Как было показано в Главе 2, дифференциальному уравнению (2.1) соответствует передаточная функция
, (2.6)
где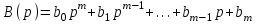
,
.
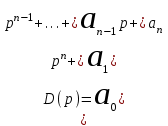Знаменатель передаточной функции – характеристический полином. Будучи приравнен нулю, он дает характеристическое уравнение:
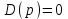(5.3)
Дифференциальные уравнения (2.1), (5.1) и передаточная функция (2.6) описывают разомкнутую систему, следовательно, характеристическое уравнение (5.3) тоже относится к разомкнутой системе.
Зная передаточную функцию разомкнутой системы
W(p), можно записать передаточную функцию замкнутой системы:
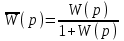. (4.6)
Заменяя W(p) по формуле (2.6), получаем:
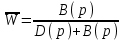. (5.4)
Знаменатель – характеристический полином замкнутой системы.
Сравнивая формулы (5.7) и (2.6), по аналогии заключаем, что уравнение
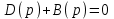(5.5)
представляет собой характеристическое уравнение замкнутой системы. Поделив (5.5) на D(p), получаем характеристическое уравнение замкнутой системы, выраженное через передаточную функцию разомкнутой системы:
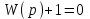. (5.6)
П
ример 5.1.
Дано дифференциальное уравнение разомкнутой системы:
.
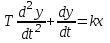Найти характеристическое уравнение и его корни.
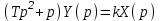
и передаточную функцию системы:
.
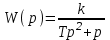Полиномы числителя и знаменателя имеют вид:
, 
.
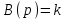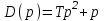Характеристическое уравнение разомкнутой системы D(p) = 0, то есть,
.
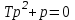Корни этого характеристического уравнения действительные:
, 
.
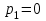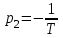Пример 5.2.
Используя дифференциальное уравнение предыдущего примера, найти характеристическое уравнение и его корни для замкнутой системы.
Подставляя передаточную функцию разомкнутой системы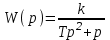 в формулу (5.6), получаем характеристическое уравнение замкнутой системы:
.
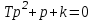Его корни:
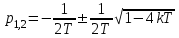
На исходной схеме с выхода звена уходит сигнал Х2. На эквивалентной схеме с выхода этого звена должен уходить сигнал Х4. Такое возможно, если входным сигналом будет не Х1, а какой-то другой, Y2. В свою очередь Y2 обязан быть суммой Х1 и сигнала Y1, который будет преобразованием входного сигнала Х3 корректирующим звеном с передаточной функцией Kк. Передаточную функцию Kк требуется определить. Выразим эти умозаключения операторным уравнением
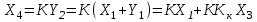
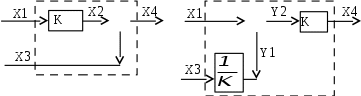
| Рис. 4.14 а. Система до перестановки | Рис. 4.14 б. Эквивалентная структурная схема |
Так как сигнал Х4тот же, что и в исходном операторном уравнении, должно выполняться равенство
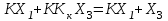
Из него следует, что корректирующим звеном в линии сигнала Х3 будет Kк = 1/K. Что и изображено на схеме рис. 4.14 б.
Вывод: перенос сумматора с выхода звена на вход, при условии сохранения входных и выходного сигналов системы, требует включения в линию второго подаваемого на сумматор сигнала звена с передаточной функцией, обратной заданной.
4.4.2.4. Перенос сумматора с входа звена на выход
Исходная схема имеет два входных сигнала Х1 и Х2 и один выходной сигнал Х4, рис. 4.15 а. Выходной сигнал связан с входными уравнением Х4 = KХ3 = K Х1 + K Х2. Эквивалентная схема должна иметь те же входные и выходной сигналы.
Чтобы в эквивалентной схеме получить тот же сигнал Х4, в линию входного сигнала Х2 следует ввести корректирующее звено с передаточной функцией Kк. Тогда сигнал Х4 окажется связанным с входными сигналами уравнением:
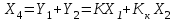
| Рис. 4.15 а. Система до перестановки | Рис. 4.15 б. Эквивалентная структурная схема |
Сравнивая его с исходным уравнением Х4 = K Х1 + KХ2, приходим к заключению, что корректирующая передаточная функция Kк= K. Что и обозначено на схеме рис. 4.15 б.
Вывод: перенос сумматора с входа звена на выход, при условии сохранения входных и выходных сигналов системы, требует включения в линию второго подаваемого на сумматор сигнала звена, с передаточной функцией, одинаковой с заданной.
П
ример 4.10.
Найти передаточную функцию системы, структурная схема которой изображена на рис. 4.16.
Рис. 4.16. Исходная структурная схема
Звенья с передаточными функциями K3 и K4 соединены параллельно. Сделаем первое упрощение схемы, заменив их передаточной функцией
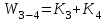. Из схемы устраняются узел 2 и сумматор С4. Также переставим сумматоры С1 и С2. Схема примет вид: Обнаруживаем, что звено с передаточной функцией K1 охвачено положительной обратной связью через звено с передаточной функцией K2. Схема упрощается, если ввести передаточную функцию
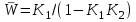. Сумматор С1 и узел 1 устраняются. Остается: Дальнейшее упрощение схемы связано с переносом узла 4 с выхода звена K5 на его вход и перестановкой с узлом 3. В ответвлении от узла 4 появляется звено K5, последовательно включенное со звеном K6.
Обнаруживается замкнутый контур из звеньев с передаточными функциями W3-4, K5 и K6. Его можно заменить звеном с передаточной функцией
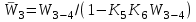. Сумматор С3 и узел 4 устраняются. Схема приобретает вид:
Выражая последний замкнутый контур звеном
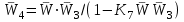, приходим к схеме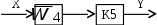 Следовательно, передаточная функция системы, имеющей структурную схему, показанную на рис. 4.16, есть
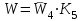,или, в развернутом виде,
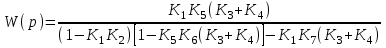.Литература
1. Бесекерский В.А., Попов Е.П. Теория автоматического управления. – СПб , изд-во «Профессия» , 2004. – 752 с.
2. Егоров К.В. Основы теории автоматического регулирования. – М.: Энергия, 1967. – 648 с.
3. Макаров И.М., Менский Б.М. Линейные автоматические системы. – М.: Машиностроение, 1947. – 464 с.
4. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. – М.: Машиностроение, 1973. – 606 с.
5.1. Понятие об устойчивости
Система, которая после завершения переходного процесса приходит к состоянию установившегося равновесия, называется устойчивой. В устойчивой системе регулируемая величина со временем стремится к постоянному значению.
Система называется неустойчивой, если после устранения воздействия она удаляется от состояния равновесия или совершает около него недопустимо большие колебания. В неустойчивой системе регулируемая величина со временем возрастает.
Если заранее выяснить, будет ли регулируемая величина неограниченно возрастать после воздействия, можно получить ответ на вопрос об устойчивости системы.
Характер воздействия на систему и поведение управляемой величины описывается дифференциальным уравнением. Оно было записано для разомкнутой системы в главе 2:
(2.1)Когда воздействие на систему прекращается, правая часть обращается в ноль и дальнейшее изменение управляемой величины описывается однородным дифференциальным уравнением
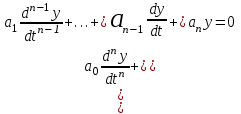. (5.1)Решение однородного уравнения показывает, возрастает или не возрастает со временем управляемая величина. Решение ищут, полагая y(t) = ept. Беря производные и подставляя в уравнение (5.1) находят характеристическое уравнение
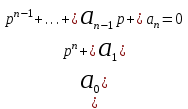(2.7)решая которое, получают корни pi. Полное решение уравнения (5.1) слагается из экспонент:
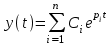(5.2)где Сi – постоянные интегрирования.
Функция y(t) – описывает переходной процесс; он полностью определяется значением корней pi.
Корни характеристического уравнения могут быть действительными, комплексными, мнимыми. Если корни действительные и отрицательные, каждая экспонента со временем стремится к нулю, следовательно, y(t) 0. По окончании переходного процесса система приходит к состоянию установившегося равновесия.
Если корни действительные и положительные, все экспоненты со временем неограниченно возрастают, y(t) ∞. Процесс неустойчивый, система удаляется от состояния равновесия.
Если корни комплексно-сопряженные с отрицательной действительной частью, каждая экспонента со временем стремится к нулю, имея колебательную составляющую. И в этом случае y(t) 0. Система, следовательно, устойчивая.
В случае комплексно-сопряженных корней с положительной действительной частьюсистема неустойчивая.
При наличии чисто мнимых корней выходная величина совершает гармонические колебания. Мнимые корни соответствуют границе устойчивости.
Итак, система устойчива только в том случае, когда действительная часть корней характеристического уравнения отрицательная.
Для суждения об устойчивости необязательно решать дифференциальное уравнение. Как было показано в Главе 2, дифференциальному уравнению (2.1) соответствует передаточная функция
, (2.6)где
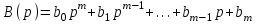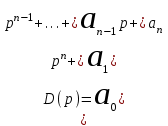, .Знаменатель передаточной функции – характеристический полином. Будучи приравнен нулю, он дает характеристическое уравнение:
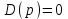(5.3)Дифференциальные уравнения (2.1), (5.1) и передаточная функция (2.6) описывают разомкнутую систему, следовательно, характеристическое уравнение (5.3) тоже относится к разомкнутой системе.
Зная передаточную функцию разомкнутой системы
W(p), можно записать передаточную функцию замкнутой системы:
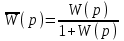. (4.6)Заменяя W(p) по формуле (2.6), получаем:
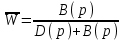. (5.4)Знаменатель – характеристический полином замкнутой системы.
Сравнивая формулы (5.7) и (2.6), по аналогии заключаем, что уравнение
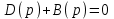(5.5)представляет собой характеристическое уравнение замкнутой системы. Поделив (5.5) на D(p), получаем характеристическое уравнение замкнутой системы, выраженное через передаточную функцию разомкнутой системы:
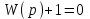. (5.6)П
ример 5.1.
Дано дифференциальное уравнение разомкнутой системы:
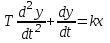.Найти характеристическое уравнение и его корни.
Записываем операторное уравнение
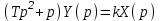
и передаточную функцию системы:
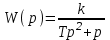.Полиномы числителя и знаменателя имеют вид:
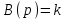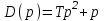, .Характеристическое уравнение разомкнутой системы D(p) = 0, то есть,
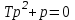.Корни этого характеристического уравнения действительные:
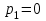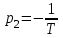, . Пример 5.2.
Используя дифференциальное уравнение предыдущего примера, найти характеристическое уравнение и его корни для замкнутой системы.
Подставляя передаточную функцию разомкнутой системы
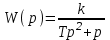в формулу (5.6), получаем характеристическое уравнение замкнутой системы: 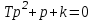.Его корни: