Файл: Пояснительная записка к дипломному проекту дп 23. 05. 03. К11псд(с)Л031. Пз студент иифо.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 306
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.7 Расчёт инвентарного парка и процента неисправных локомотивов
Инвентарный парк депо рассчитывается по формуле
Минв = ∑Мэ + ∑Мрем + Мрез + Мком + Мзап + Ма, (3.37)
Где ∑Мэ–локомотивы всех видов движения, находящиеся в эксплуатации;
∑Мрем–локомотивы, находящиеся во всех видах ремонта и ТО-3;
Мрез–локомотивы, находящиеся в резерве управления дороги (8–15 % от ∑Мэ);
Мком–число локомотивов, откомандированных в другие депо;
Мзап– локомотивы запаса РЖД(3–5 % от ∑Мэ);
Ма– локомотивы в аренде.
Общий процент неисправных локомотивов aн определяется как отношение неисправных локомотивов, одновременно находящихся в ремонте в депо и на заводе, к суммарному парку локомотивов, находящихся в распоряжении депо во всех видах движения и работы:
aн = 100 ∑Мрем/Мрд , (3.38)
где Мрд– парк локомотивов, находящихся в распоряжении депо.
Парк в распоряжении депо состоит из локомотивов, находящихся в эксплуатации, в ремонте и резерве управления дороги
Мрд = ∑Мэ + ∑Мрем+ Мрез. (3.39)
Деповской процент неисправных локомотивов определяется по формуле
aдн = 100(∑Мрем–∑Mзав) /Мрд , (3.40)
а заводской – по формуле
aзн = 100 ( ∑Mзав ) /Мрд, (3.41)
где ∑Mзав– общее количество локомотивов, находящихся в заводском ремонте (КР и СР).
Определяем число локомотивов, находящихся в резерве управления дороги и запасе ОАО "РЖД".
Мрез= 0,15 ∑Мэ, Мзап= 0,05 ∑Мэ,
Определяем инвентарный парк локомотивов
Минв = ∑Мэ + ∑Мрем + Мрез+ Мком+ Мзап + Ма ,
Определяем парк локомотивов, находящийся в распоряжении депо
Мрд = ∑Мэ + ∑Мрем+ Мрез,
Определяем общий процент неисправных локомотивов (f = ∑Мрем)
aн = 100 ∑Мрем/Мрд,
Определяем деповской процент неисправных локомотивов
aдн = 100(∑Мрем–∑M
зав) /Мрд,
Определяем заводской процент неисправных локомотивов
aзн = 100 ( ∑Mзав ) /Мрд,
Таблица 3.17 – Результаты расчёта инвентарного парка депо.
| Наименование показателя | Величина показателя |
| Эксплуатируемый парк, единиц | 94 |
| В ремонте, единиц | 19 |
| В резерве управления дороги, единиц | 0 |
| В распоряжении депо, единиц | 120 |
| Запас ОАО "РЖД", единиц | 4 |
| Инвентарный парк, единиц | 154 |
| Общий процент неисправных локомотивов | 10,8 |
| Деповской процент неисправных локомотивов | 6,8 |
| Заводской процент неисправных локомотивов | 0,34 |
4 РАЗРАБОТКА МЕРОПРИЯТИЙ ПО УВЕЛИЧЕНИЮ РЕСУРСА МОТОРНО-ОСЕВЫХ ПОДШИПНИКОВ, ИССЛЕДОВАИЕ СИЛ, ДЕЙСТВУЮЩИХ В ЭЛЕМЕНТАХ ТЯГОВОГО ПРИВОДА ЭЛЕКТРОВОЗОВ ВЛ80С И 2ЭС5К
4.1 Причины возникновения динамических нагрузок
На локомотив, как на механическую систему, действует большое количество различных возмущающих факторов, которые вызывают динамические силы и моменты [3, 4]. Условно их можно разделить на внешние и внутренние. К внешним относятся факторы, природа которых не зависит от свойств локомотива. К внутренним, – появление которых обусловлено свойствами локомотива. Кроме того, различают возмущения силовые, кинематические и параметрические. Внешние силовые возмущения возникают при изменении сопротивления движению поезда (локомотива), кинематические – обусловлены непрямоли-нейностью пути в профиле, вызванной переломами профиля и возвышениями рельсов, а также местными дефектами верхнего строения пути; параметрические – неравномерностью распределения диссипативных, инерционных и упругих свойств пути по его длине.
Внутренние силовые возмущения создаются электромагнитным моментом тягового двигателя и дисбалансом вращающихся частей. Внутренние кинематические возмущения возникают вследствие отклонения поверхности катания колеса от идеальной круговой и концентрической по отношению к геометрической оси колесной пары, а также вследствие кинематических погрешностей зубчатого зацепления и тяговых муфт. Параметрические возмущения возникают в результате изменения радиальной жесткости муфты по заданной координате (меняется ориентация упругих элементов в пространстве при ее вращении), а также условий сцепления в контакте колеса с рельсом.
Указанные факторы, как правило, действуют одновременно при движении локомотива по пути. Однако так как локомотив и, в частности, тяговый привод (ТП) представляет собой динамическую систему со многими степенями свободы, то результат воздействия каждого из указанных факторов проявляется по-разному.
Для того чтобы определить динамические нагрузки, характер их изменения, необходимо знать расчетные режимы работы ТП, соответствующие им возмущения, иметь механоматематическую модель тягового привода и методы ее исследования.
4.2\Силы, действующие на шестерню, статор тягового электродвигателя, колесную пару с зубчатым колесом электровоза ВЛ80С
Схема сил, действующих на шестерню, представлена на рисунке 4.1 [3].

Рисунок 4.1 – Схема сил, действующих на шестерню
Выделим из общей схемы тягового привода только якорь двигателя с шестернями (рисунок 4.1). На якорь с шестерней действует электромагнитный момент
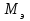 , который уравновешивается моментом от сил в зацеплении (сила со стороны зубчатого колеса)
, который уравновешивается моментом от сил в зацеплении (сила со стороны зубчатого колеса) 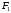 и реакцией в якорных подшипниках
и реакцией в якорных подшипниках 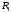 . Из рисунка (4.2) видно, что
. Из рисунка (4.2) видно, что 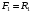 .
.Сила в зацеплении
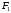 , кН, определяется следующим выражением
, кН, определяется следующим выражением
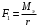 , (4.1)
, (4.1)где
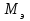
– электромагнитный момент, кН·м;
 – радиус шестерни, м.
– радиус шестерни, м.Рассмотрим силы, действующие на статор тягового электродвигателя одного колесно-моторного блока (рисунок 4.2) [3].
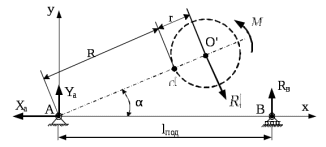
Рисунок 4.2 – Схема сил, действующих на статор одного тягового электродвигателя
Уравнение проекций на осьx имеет вид
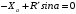 , (4.2)
, (4.2)где
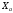 – горизонтальная реакция в неподвижной опоре, кН;
– горизонтальная реакция в неподвижной опоре, кН;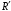 – сила в подшипниках статора, кН;
– сила в подшипниках статора, кН; – угол между линией централи двигателя и плоскостью пути, град.
– угол между линией централи двигателя и плоскостью пути, град.Так как
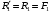 , то реакция реакцию
, то реакция реакцию 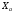 по уравнению
по уравнению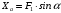 . (4.3)
. (4.3)Уравнение проекций на ось y имеет вид
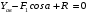 , (4.4)
, (4.4)где
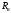 – реакция в подвижной опоре В, кН;
– реакция в подвижной опоре В, кН;Определяем реакцию
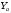 по уравнению
по уравнению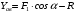 . (4.5)
. (4.5)Уравнение моментов относительно точки А имеет вид
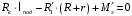 , (4.6)
, (4.6)где
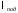 – расстояние между точками подвески двигателя, м;
– расстояние между точками подвески двигателя, м;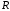 – радиус зубчатого колеса, м;
– радиус зубчатого колеса, м;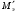 – электромагнитный момент, действующий на статор тягового электродвигателя, кН·м.
– электромагнитный момент, действующий на статор тягового электродвигателя, кН·м.С учетом того, что
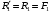 ,
, 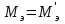 и выражения (3.4), реакция
и выражения (3.4), реакция 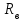 определяем
определяем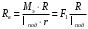 , (4.7)
, (4.7)Для практических расчетов силу
 в зубчатом зацеплении определяем из условия реализации электровозом максимального коэффициента сцепления, тогда
в зубчатом зацеплении определяем из условия реализации электровозом максимального коэффициента сцепления, тогда
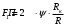 , (4.8)
, (4.8)где
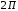 – нагрузка от колесной пары на рельсы,
– нагрузка от колесной пары на рельсы, 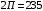 кН;
кН;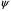 – коэффициент сцепления колеса с рельсом,
– коэффициент сцепления колеса с рельсом, 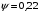 ;
;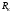 – радиус колеса по кругу катания,
– радиус колеса по кругу катания, 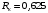 м.
м.Равнодействующая сила, действующая на моторно-осевой подшипник, определяется
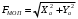 . (4.9)
. (4.9)Момент
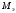 передается на колесную пару с зубчатыми колесами в виде силы
передается на колесную пару с зубчатыми колесами в виде силы 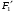 от шестерни (рисунок 4.3). При этом на ободе колеса появляется сила
от шестерни (рисунок 4.3). При этом на ободе колеса появляется сила 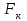 , действующая со стороны рельса и сила
, действующая со стороны рельса и сила 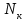 . Со стороны тягового двигателя действуют силы
. Со стороны тягового двигателя действуют силы 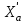 ,
, 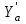 . Силы
. Силы 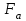 и
и 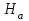 действуют на шейки колесных пар от букс. Запишем уравнения проекций сил на оси x и y.
действуют на шейки колесных пар от букс. Запишем уравнения проекций сил на оси x и y.Уравнение проекций на ось x имеет вид
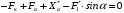 , (4.10)
, (4.10)где
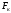 – касательная (горизонтальная) сила тяги на ободе колеса, кН;
– касательная (горизонтальная) сила тяги на ободе колеса, кН;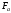 – горизонтальная сила, действующая на шейку колесной пары от
– горизонтальная сила, действующая на шейку колесной пары от буксы, кН;
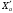 – горизонтальная сила со стороны ТЭД, кН;
– горизонтальная сила со стороны ТЭД, кН;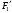 – сила от шестерни на зубчатое колесо, кН
– сила от шестерни на зубчатое колесо, кН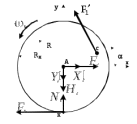
Рисунок 4.3 – схема сил, действующих на колесную пару с зубчатыми колесами
С учетом выражения (4.3) и
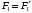 получаем
получаем