Файл: Методичка по механике вся Печать новый вариант12г.doc

Основные формулы кинематики

Движения тел классифицируют по форме траектории и виду кинематических зависимостей (законов движения). По форме траектории различают прямолинейное и криволинейное движения, в частности, движение по окружности и движение тела, брошенного под углом к горизонту (траектория – парабола). Основными видами движения являются равномерное и равнопеременное (в частности, равноускоренное или равнозамедленное), т.е. движение с постоянным ускорением (например, в поле силы тяжести).

Таблица 1. Классификация механических движений

Для задания положения используются 3 подхода:

1. расстояние вдоль траектории от некоторой начальной точки,

2. координатный – с помощью системы координат,

3. векторный – с помощью радиус-вектора.

В каждом из этих случаев формула закона движения своя.

Равномерное движение– движение с постоянной скоростью (какпо модулю, так ипо направлению). Такое движение – всегдапрямолинейноедвижение. В этом случае путь всегда равен величине перемещенияS.

Закон равномерного движения:

(1) ,- (1-я форма), где- модуль скорости,

или

(1’) -(2-я форма), где- проекция скорости движения на осьх.

Если скорость меняется (по величине илипо направлению), то движение считаетсянеравномерным.

Методические указания.При ответе на вопрос «Как меняется скорость тела?» необходимо выбрать один из следующих ответов:

1. скорость меняется только по направлению (величина скорости постоянна);

2. скорость меняется только по модулю (направление постоянно);

3. скорость меняется и по модулю и по направлению;

4. скорость НЕ меняется (модуль И направление постоянны!) – в случае отрицательного ответа.

Наличие нескольких способов изменения скорости обусловлено тем, что это векторная величина. Для сравнения отметим, что скалярная величина характеризуется одним параметром - числовым значением (или только модуль – неотрицательное число, или, для некоторых скаляров, модуль и знак: «плюс» или «минус» - т.е. любое действительное число). Так, проекция скорости на ось есть скалярная величина определенного знака, в отличие от величины пройденного пути.

Равнопеременное движение (равноускоренное или равнозамедленное,но не только!) – движение с постоянным ускорением по следующему закону:

(2) -зависимость путиSот времени (форма 1),

, .

- модуль начальной скорость,а – модуль ускорения,t– затраченный промежуток времени.

иначе

(3) - зависимость координаты от времени (форма 2),

(4) ,.

Равенства, записанные в скалярной форме, требуют учета знаков перед значениями векторных величин!.

Методические указания. При записи закона движения в форме 2 направления всех векторных величин сравниваются с выбранным положительным направлением осей координат, поэтому выбор знака «+» или «-» осуществляется и перед скоростью и перед ускорением. Форма 1 соответствует выбору положительного направления в сторону самого движения (по направлению начальной скорости).

Замечание. При решении задач часто очень удобно использовать формулу, являющуюся следствием исключения из формул (2) и (4) параметра t:

(5) - путь, пройденный при движении с ускорениемaна участке изменения скорости от до (необходимо учесть знак! В случае равнозамедленного движения величины и в числителе формулынадо поменять местами).

Равномерное движение по окружности – движение по окружности спостоянной по модулюскоростью. Скорость как векторная величина МЕНЯЕТСЯ, но лишь по направлению(см. выше вариант 1). Поэтому в этом случае есть ускорение – центростремительное (нормальное), зависящее от модуля линейной скорости:

(6), гдеR– радиус окружности.

При движении по окружности тело проходит за единицу времени некоторое расстояние вдоль траектории – определяемое линейнойскоростью. В то же время тело за единицу времени поворачивается на некоторый угол – определяемый угловой скоростью.Угловая скорость (при равномерном движении по окружности!) численно равна углу поворота за единицу времени:

(7) ,где- угол поворота за время.

Угловая скорость также имеет направление, которое определяется по правилу правого винта³, т.е. она направлена перпендикулярно плоскости окружности.

Замечание. В случае неравномерного движения по окружности необходимо говорить о мгновенном значении угловой скорости, которое находится как производная от угла поворота по времени: . Кроме того, угловая скорость имеет и направление, которое находится по правилу правого буравчика; в частности, угловая скорость перпендикулярна плоскости вращения. Т.е. угловая скорость в общем также является векторной величиной!

Частота вращения n- количество оборотов в единицу времени. За один оборот принимается поворот на угол.Период вращенияТ– время одного полного оборота. Основные формулы:

(8) ;(9) ;(10) .

Каждой угловой величине можно поставить в соответствие величину линейную (см. табл.2):

Таблица 2. Связь линейных и угловых величин

Связь линейных и угловых величин можно представить схематично:

Угловая величина R = Линейная величина

Например, имеем формулы:

(11) ;(12)

и, как следствие формулы (6), получаем: (13) ,

где R- радиус окружности,a_n - центростремительное ускорение.

Методические указания. Если скорость меняется только по направлению, т.е. есть лишь ускорение, перпендикулярное (нормальное - от слова «нормаль») скорости, то его чаще называют центростремительным (как в случае равномерного движения по окружности). Если же имеет место изменение обоих параметров (модуля и направления), то соответственно каж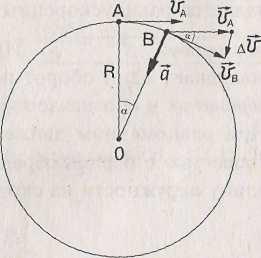дому из них выделяют отдельно две составляющие ускорения:тангенциальное (касательное) ускорение а_, которое направлено вдоль скорости и характеризует быстроту изменения величины скорости, и нормальное (перпендикулярное скорости) ускорение а_n, относящееся к изменению направления скорости. Тогда полное ускорение равно их векторной сумме:

.

Отдельную группу составляют задачи на среднюю скорость движения. О средней скорости говорят, когда в течение некоторого времени t значение скорости менялось. Тогда если бы тело двигалось с постоянной скоростью равной V_ср, то за это время t оно прошло бы то же самой расстояние. Поэтому по определению имеем формулу:

(14) .

Другими словами, введение средней скорости там, где движение явно не равномерное (истинный вид движения может быть не известен, сложен или переменчив) дает как бы первое приближение этого движения, заменяя его равномерным.

Методические указания. Анализируя методы решения задач, можно отметить два случая: 1) решение «от данного к искомому» или «от начала», основано на применении типичных для данной ситуации рассуждений до тех пор, пока не придем к тому, что требуется; 2) решение «от искомого к данным» или «от конца», основано на записи формул, относящихся к искомой величине (чаще, ее определение) и постепенном выражении входящих в нее неизвестных переменных через данные задачи. Так, решение задачи, где требуется найти среднюю скорость, должно начинаться с записи формулы (14). После этого на основе условия задачи выделяются основные неизвестные и через них и данные задачи выражаются все другие неизвестные. Затем при подстановке в исходную формулу производится сокращение основных неизвестных и получается общая формула решения.