Файл: Блім бойынша жиынты.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 481

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Шығармашылық топ автор-қҧрастырушылар:

Пікір жазған:

1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР

Оқу мақсаттары:

І –нҧсқа

[1]

[1]

– нҧсқа

2 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР

Тақырып

Оқу мақсаттары:

– нҧсқа

нҧсқа

3 -ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР

Тақырып

Оқу мақсаттары:

ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР

Тақырып

Оқу мақсаттары:

І –нҧсқа

[4]

[4]

«СТАТИСТИКА ЭЛЕМЕНТТЕРІ» бөлімі бойынша жиынтық бағалау

Оқу мақсаттары:

І –нҧсқа

[2]

[2]

ІІ –нҧсқа

[2]

[2]

– нҧсқа

ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР

Тақырып

Оқу мақсаттары:

І –нҧсқа

– нҧсқа

БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР.

1 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ

Тақырып

Бағалаукритерилері

Ойлау дағдыларының деңгейлері: Қолдану

нҧсқа

нҧсқа

2 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ

АРАСЫНДАҒЫ ҚАТЫСТАР» бөлімі бойынша жиынтық бағалау

Тақырыптар

Оқумақсаттары

Бағалаукритерийлері

Тапсырмалар:

2 нҧсқа

3 –нҧсқа

4 –нҧсқа

3 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ

Тақырып

Бағалаукриетрийлері

–нҧсқа

4 ТОҚСАНҒА АРНАЛҒАН БӨЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ

жиынтық бағалау

Тақырып

Оқумақсаттары

Бағалаукритерийлері

– нҧсқа

ТОҚСАНДАҚ ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР. Алгебра

І тоқсанға арналған ТЖБ

Бөлім

Мақсаттар

Ойлау дағдыларының деңгейі: Қолдану

ІІ тоқсанға арналған ТЖБ

Оқу мақсаттары

І нҧсқа

Бағалау кестесі

ІІІ тоқсанға арналған ТЖБ

Бөлім

Оқу мақсаттары

І нҧсқа

ІІ нҧсқа

ІV тоқсанға арналған ТЖБ

Оқу мақсаттары

І нҧсқа

ІІ нҧсқа

ТОҚСАНДАҚ ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР. Геометрия

І тоқсан ҥшін ТЖБ

Балл саны - 20

нҧсқа

Балл қою схемасы

ІІ тоқсан ҥшін ТЖБ

Балл саны - 20

ІІІ тоқсан ҥшін ТЖБ

Балл саны - 20

4 тоқсан ҥшін ТЖБ

Балл саны - 20





  1. Жерден жоғары лақтырылған доптың жерден биіктігін мына формуламен ӛрнектейді: (????) 12???? − 5????2 −биіктік м есебімен ???? −уақыт сек есебімен.

а) ҥш секунд ӛткенде доп қандай биіктікте болады?

б) Неше секунд ӛткеннен кейін доп 7 м биіктікте болады? в) Доптың ең жоғарғы биіктігі қандай?
Бағалау кестесі






І нҧсқа
ІІ нҧсқа



1
Е
Е
1

2
(1; 7)
(−3; 5)
1



3
а) x = 3
а) x = 2
1

б) x2 − 6x − 7 = 0
б) x2 − 4x − 5 = 0
1

(7; 0) (−1; 0)
( 5; 0) (−1; 0)
1

в) (0 ; −7)
в) (0 ; −5)
1

г) график салады
г) график салады
1

4



[15,9;16,4)
[16,4; 16,9)
[16,9; 17,4)
[17,4; 17,9)
[17,9; 18,4)
[18,4; 18,9]






[175; 195)
[196; 215)
[215; 235)
[235; 255)
[255; 275]



1













[15,9; 16,4)
[16,4; 16,9)
[16,9; 17,4)
[17,4; 17,9)
[17,9; 18,4)
[18,4; 18,9]






[175; 195)
[196; 215)
[215; 235)
[235; 255)
[255; 275]



1

2
2
1
1
1
3
2
2
2
1
3

Арифметикалық ортасы 17,4
Арифметикалық ортасы 226,5
1

5
20 − 20 = 1,

x x + 1

x −2 –ші турист жылдамдығы
300 − 300 = 1

x x + 10

x- 2- ші кӛлік жылдамдығы
1




20(x + 1) − 20x − x(x + 1) = 0
300(x + 10) − 300x − x(x + 10) = 0
1






x(x + 1)


x(x + 10)






x2 + x − 20 = 0
x2 + 10x − 3000 = 0
1




x1 = 4;

x2 = −5 – есеп шартын қанағаттандырмайды
x1 = 50;

x2 = −60 – есеп шартын қанағаттандырмайды
1




4 км/с 5 км/с
50 км/с 60 км/с
1

6
t = 2 ; 9 · 2 − 2 · 4 = 10 м
t = 3 12 · 3 − 5 · 9 = −9 ; 9 м
1




9t − 2t2 = 10
12t − 5t2 = 7
1




t1 = 2,5 c t2 = 2 c
t1 = 7 c t2 = 5 c
1




(t) = 9t − 2t2 тармағы тӛмен
(t) = 12t − 5t2 тармағы тӛмен
1




қараған парабла функциясының
қараған парабла функциясының






графигі, доптың ең биік тҥктесі ол
графигі, доптың ең биік тҥктесі ол






парабола тӛбесінің координатасы
парабола тӛбесінің координатасы






b2 − 4ac 81 − 4(−2) 89

4a = 4(−2) = −8 = −11,125
b2 − 4ac 144 − 4(−5) 164

4a = 4(−5) = −20 = −8,2
1




max = 11,125 м биіктік
max = 8,2 м биіктік



Барлық балл
20

ІV тоқсанға арналған ТЖБ



Бөлім Квадрат теңсіздік Рационал теңсіздік Теңсіздіктер жҥйесін шешу

Оқу мақсаттары


        1. квадрат теңсіздіктерді шешу

        2. рационал теңсіздіктерді шешу

        3. біреуі сызықтық, екіншісі - квадрат екі теңсіздіктен қҧралған жҥйелерді шешу

        4. екі квадрат теңсіздіктердің біріккен жҥйесін шешу


Ойлау дағдыларының деңгейі: Білу және тҥсіну. Қолдану

Орындау уақыты 40 минут

І нҧсқа





  1. [1 балл] Теңсіздікті шешіңіз: (x − 3)(x + 4) < 0

А) (3; 4)

В) (−4; 3)

С) (− ; −4) (3; )
D) [−3; 3) (4; )

Е) (− ; −4] [3; )




  1. [1 балл] = x2 − 2x + 3 функциясының графигін пайдаланып ????2 − 2???? − 3 ≥ 0

теңсіздіктің шешімін табыңыз




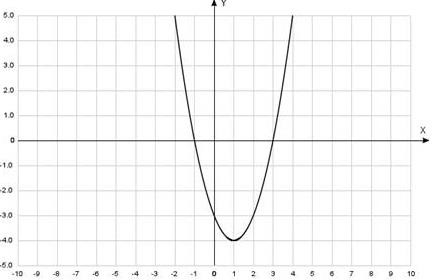
А) (−1; 3)

В) (− ; −1) (3; )

С) (− ; 2)
D) (− ; −1)] [3; )

E) [−1; 3]




  1. [3 балл] Теңсіздіктің бҥтін шешімдерін табыңыз: 2????2 − 7???? − 4 ≤ 0


  2. 2
    [5 баллТеңсіздіктер жҥйесін шешіңіз: { 8???? − 2 < ???? − 1

2???? − ???? − 1 ≤ 0



  1. 2
    [5 балл] Теңсіздікті шешіңіз : ????2(3−????) ≤ 0

???? −8????+16


  1. [5 балл] Теңсіздіктер жҥйесін шешіңіз : {????2 − 3???? + 4 0

????2 − 16 ≤ 0

ІІ нҧсқа





  1. [1 балл] Теңсіздікті шешіңіз: (???? − 7)(???? + 5) 0

А) (5; 7)

В) (− ; −5) (7; )

С) (−5; 7)
D) [−5; 5) (7; )

Е) (− ; −5] [7; )




  1. [1 балл] = x2 − 8x + 7 функция графигін пайдаланып ????2 − 8???? + 7 ≥ 0 иеңсіздігін шешіңіз:




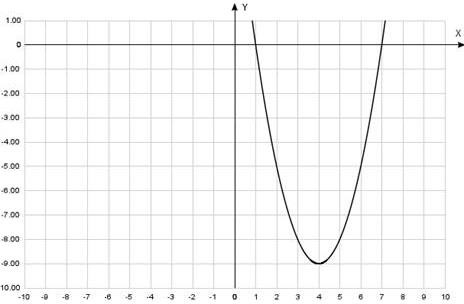
.А) (1; 7)

В) (− ; 1) (7; )

С) (− ; 1)
D) (− ; 1)] [7; )

E) [1; 7]




  1. [3 балл] Теңсіздіктің бҥтін шешімін табыңыз: ????2 − 3???? − 4 < 0

  2. [5 балл] Теңсіздіктер жҥйесін шешіңіз: {7(3???? + 2) − 3(7x + 2) < 2????

????2 + 3???? − 40 ≤ 0



  1. 2
    [5 балл] Теңсіздікті шешіңіз : ????2(4−????) ≤ 0

???? −10????+25


  1. [5 балл] Теңсіздіктер жҥйесін шешіңіз : {????2 − 5???? + 7 0

????2 ≤ 81
Балл қою кестесі






І нҧсқа
ІІ нҧсқа






№
жауаптар
жауаптар
балл
Қосымша

мәліметтер

1
В
В
1



2
Е
Е
1




3
x1 = −0,5; x2 = 4
x1 = −1; x2 = 4
1



x ∈ (−0.5; 4)
x ∈ (−0.5; 4)
1

Жауабы: 0, 1,2,3
Жауабы: 0, 1,2,3
1




Квадрат ҥшмҥшенің тҥбірлерін табады x1 =

1 ; x2 = − 1

2
Квадрат ҥшмҥшенің
1






тҥбірлерін табады x1 =






−8; x2 = 5






Бірінші теңсіздік

x ∈ [− 1 ; 1]

2
Бірінші теңсіздік

x ∈ [−8; 5]
1

4






Екінші теңсіздікті ax

Екінші теңсіздікті ax

1




???????? < 7x < 1 тҥріне
???????? < 2x < 8 тҥріне






келтіреді
келтіреді






x < 1
x < 4
1




7






x ∈ [− 1 ; 1)
x ∈ [−8;4)
1




2 7






x2(3 − x)

(x − 4)2 ≤ 0
x2(4 − x)

(x − 5)2 ≤ 0
1
Басқа тәсілмен











шешуі мҥмкін


5
x = 0 x = 3 x = 4
x = 0 x = 4 x = 5
1



Интервалдар әдісін
Интервалдар әдісін
1




қолданады
қолданады









Аралықтардығы
Аралықтардығы
1






таңбаларды анықтайды
таңбаларды анықтайды









Жауабы: x ∈ {0} [3;4)

Жауабы: x ∈ {0} [4;5)

1






(4; ∞)
(5; ∞)









Бірінші теңсіздік ҥшін < 0
Бірінші теңсіздік ҥшін < 0
1






болатынын алады
болатынын алады






x ∈ R
x ∈ R
1



6
Екінші теңсіздік ҥшін
Екінші теңсіздік ҥшін
1
Басқа тәсілмен




(x − 4)(x + 4) ≤ 0 алады
(x − 9)(x + 9) ≤ 0 алады



шешуі мҥмкін




x ∈ [−4; 4]
x ∈ [−9; 9]
1






Жауабы: x ∈ [−4; 4]
Жауабы: x ∈ [−9; 9]
1



Барлық Балл
20


Смотрите также файлы