ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 506
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
На вбивание сваи расходуется кинетическая энергия совместного движения после удара. Поэтому:
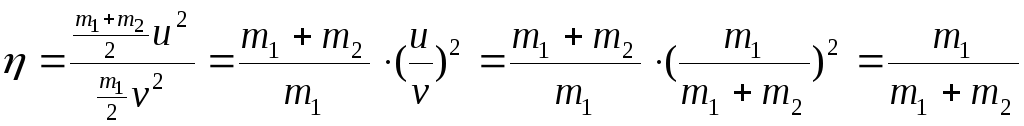 .
.
Вычислим:
![]() 80,64581%.
80,64581%.
Ответ: 81%.
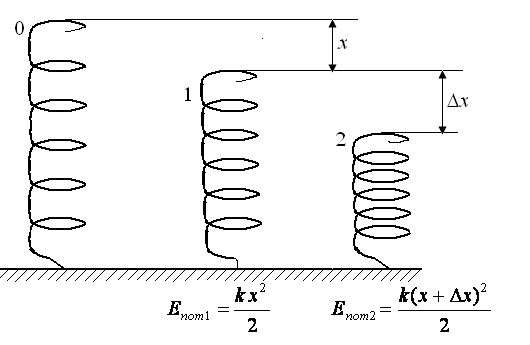
№10. Какую нужно совершить работу А, чтобы пружину жесткостьюk=800 Н/м, сжатую нах=6 см, дополнительно сжать нах=8 см?
|
Дано: k=800 Н/м, х=0,06 м, х=0,08 м.
|
Решение. Искомая работа будет равна приращению потенцальной энергии деформации пружины:
|
|
Найти: А-?
|
![]() .
.
Вычислим:
![]() 6,4
(Дж).
6,4
(Дж).
Ответ: 6,4 Дж.
№11. По круговой орбите вокруг Земли обращается спутник с периодом Т=90 мин. Определить высоту спутника. Ускорение свободного паденияgу поверхности Земли и ее радиусRсчитать известными.
|
Дано: Т=5400 с, g=9,8 м/с2, R=64105м. |
Решение.
|
|
Найти: h-?
|
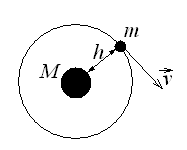
Спутник движется относительно Земли по круговой орбите, т.е. имеет центростремительное ускорение, которое ему сообщает сила тяготения. По закону всемирного тяготения:
![]() .
.
По второму закону Ньютона для спутника:
![]()
![]() .
.
Учли
выражение для центростремительного
ускорения (![]() ,
гдеr- радиус окружности
вращения). Получаем:
,
гдеr- радиус окружности
вращения). Получаем:
![]()
![]() .
.
В соответствии с определениями периода вращения и скорости скорость равна:
![]() .
.
Подставляем:
![]()
![]() .
.
Вычислим:
![]() 2,681105(м)268 (км).
2,681105(м)268 (км).
Ответ: 268 км.
№12.
Материальная точка движется по окружности
с постоянной угловой скоростью
![]() рад/с. Во сколько раз путьs,
пройденный точкой за времяt=4
с, будет больше модуля ее перемещенияr?
Принять, что в момент начала отсчета
времени радиус-векторr,
задающий положение точки на окружности,
относительно исходного положения был
повернут на угол
рад/с. Во сколько раз путьs,
пройденный точкой за времяt=4
с, будет больше модуля ее перемещенияr?
Принять, что в момент начала отсчета
времени радиус-векторr,
задающий положение точки на окружности,
относительно исходного положения был
повернут на угол![]() рад.
рад.
|
Дано:
t=4 с;
|
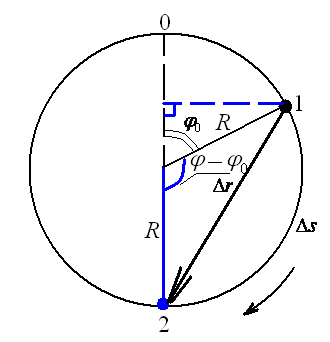
Решение.При равномерном движении по окружности положение точки можно задать указанием угла поворота относительно некоторого начала отсчета. Тогда через времяtматериальная точка окажется в положении, которому соответствует угол
Вычислим для t=4 с:
Укажем на рис. Начальное и конечное положения точки. Далее из геометрических соображений находим искомое отношение:
Вычислим:
Ответ: в 1,2 раза.
|
|
Найти:
|
|
|
|
№13. Снаряд, летевший со скоростью v=400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростьюu1=150 м/с. Определить скоростьv2большего осколка.
|
Дано: v=400 м/с, k=0,4; u1=150 м/с |
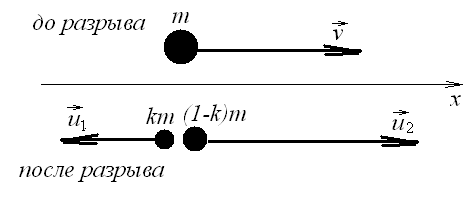
Решение. В верхней точке траектории скорость снаряда была направлена горизонтально.
Будем искать скорость большего осколка сразу после разрыва. Тогда, считая время разрыва достаточно малым, применим закон сохранения импульса для системы «m»:
Отсюда делаем вывод, что скорость большего снаряда направлена также по горизонтали. В проекции на горизонтальную ось х(направление движения снаряда в момент разрыва):
откуда выразим скорость второго осколка:
Вычислим:
Ответ: 767 м/с в направлении движения снаряда до разрыва. |
|
Найти: u2-?
|
№14. Из ствола автоматического пистолета вылетела пуля массой m1=10 г со скоростьюv=300 м/с. Затвор пистолета массойm2=200 г прижимается к стволу пружиной, жесткость которойk=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.
|
Дано: m1=10-2кг; m2=0,2 г v=300 м/с; k=25∙103Н/м
|
Решение.
|
|
Найти: х-?
|
|
|
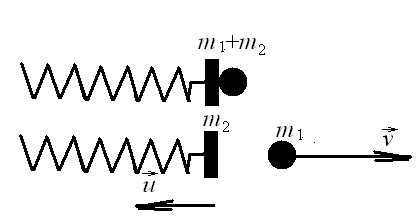
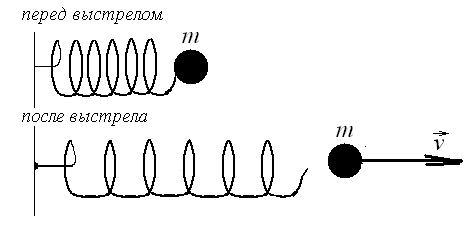
К системе «затвор-пуля» можно применить закон сохранения импульса, считая время взаимодействия достаточно малым. Тогда импульсы системы до и после взаимодействия равны. Импульс до взаимодействия (до выстрела) равен нулю, тогда суммарный импульс системы после выстрела также равен нулю, или импульс пули по значению равен импульсу затвора (а их направления противоположны):
- скорость затвора после выстрела, тогда кинетическая энергия затвора равна
Далее рассматриваем систему «затвор-пружина»: в ней действуют только потенциальные силы (сила упругости пружины). Влияние внешних сил (силы тяжести) не существенно. Тогда по закону сохранения энергии:
- искомое расстояние. Проверим размерность:
Вычислим:
Ответ: на 4 см.
|
|
№15. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки равно 0,493 м/с2, период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 0,025 м.
Дано: аmax=0,493 м/с2,
Т=2 с,
х0=0,025 м
Решение.Уравнение гармонического колебательного движения имеет вид:
![]() ,
,
где
![]() - амплитуда колебаний,
- амплитуда колебаний,![]() -
начальная фаза,- циклическая частота колебаний.
-
начальная фаза,- циклическая частота колебаний.
При максимальном отклонении от положения равновесия квазиупругая сила максимальна, т.е. имеет место равенство
![]()
![]() .
.
Циклическая частота связана с периодом колебаний:
![]() (рад/с2).
(рад/с2).
Тогда амплитуда равна
![]() (м)
(м)
В начальный момент времени, т.е. при t=0 уравнение гармонических колебаний примет вид:
![]()
![]() (рад).
(рад).
Получаем искомое уравнение
![]()
Ответ:
![]()
№16. Из пружинного пистолета с пружиной жесткостью k=150 Н/м был произведен выстрел пулей массойm=8 г. Определить скоростьvпули при вылете ее из пистолета, если пружина была сжата нах=4 см.
|
Дано: k=150 Н/м; m=8∙10-3кг; х=0,04 м
|
Решение.
|
|
Найти: v-?
|
Рассмотрим систему «пружина-пуля». В ней нет непотенциальных сил, поэтому полная механическая энергия системы сохраняется. При выстреле потенциальная энергия деформации пружины переходит в кинетическую энергию пули:
![]()
![]() .
.
Проверка размерности аналогична предыдущей задаче.
Вычислим:
![]() (м/с).
(м/с).
Ответ: 5,5 м/с.
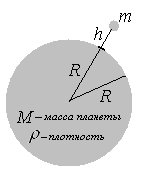
№ 17. Радиус спутника Сириуса в 7 раз, а средняя плотность в 1000 раз больше радиуса и плотности Земли. Зная ускорение свободного падения у поверхности Земли, определить ускорение свободного падения у поверхности Сириуса.
|
Дано: n=7 k=1000 g=9,8 м/с2 |
Р По закону всемирного тяготения тело mпритягивается планетойМ с силой:
|
|
Найти: g1-? |
Вблизи поверхности планеты:
![]() ,
,
где g– ускорение свободного падения для этой планеты.
Выразим массу планеты через объем и среднюю плотность ее вещества:
![]() .
.
Тогда получаем
![]() - для Земли,
- для Земли,
![]() - для Сириуса.
- для Сириуса.
![]() (м/с2).
(м/с2).
Ответ: 68,6 км/с2.
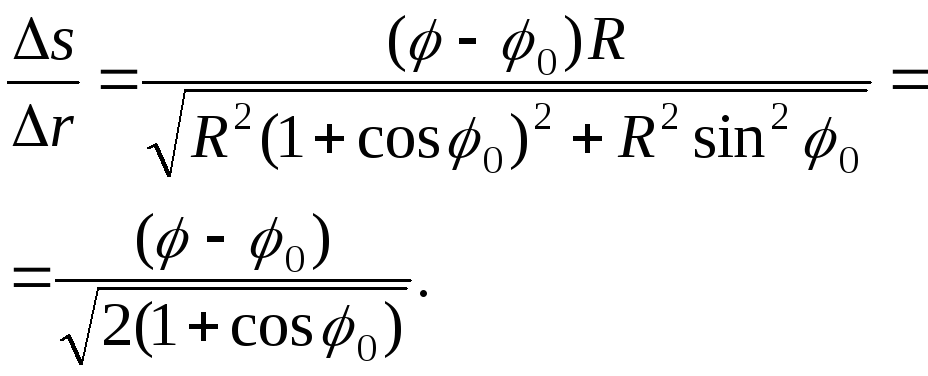
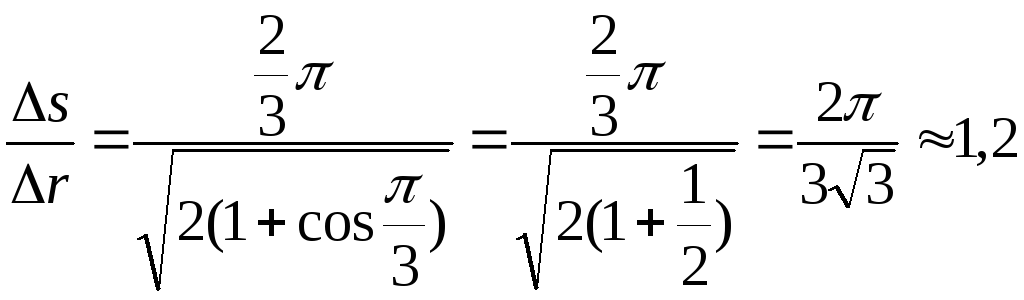
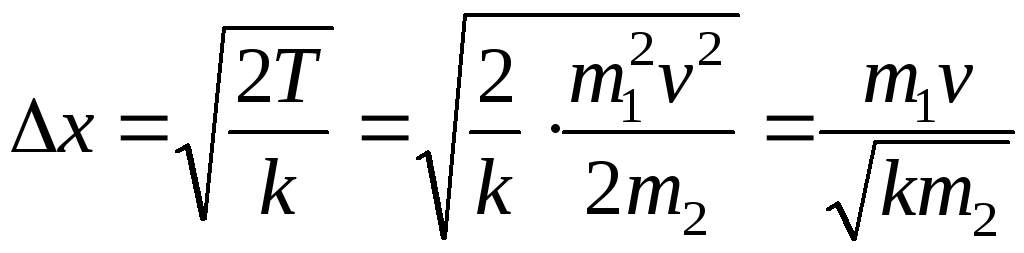 -
-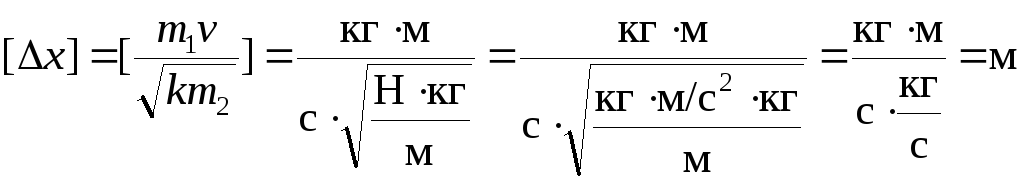 .
.
 ешение.
ешение.