Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

. (4.7)
Рассчитаем суммарные расходы при данном плане поставок (L) по формуле (4.5). Все вычисления заносим в таблицу 4.7.
Таблица 4.7 - Расчет показателей системы

	А	В	С	D	E	F	G	H	I
2	I	vi	Ki	si	fi	qi*
3	1	10	100	0,1	10	=КОРЕНЬ(2*C3*B3/D3)	=C3*B3/F3	=D3*F3	=E3*F3
4	2	20	50	0,2	5	=КОРЕНЬ(2*C4*B4/D4)	=C4*B4/F4	=D4*F4	=E4*F4
5	3	5	90	0,2	7	=КОРЕНЬ(2*C5*B5/D5)	=C5*B5/F5	=D5*F5	=E5*F5
6	4	10	20	0,1	5	=КОРЕНЬ(2*C6*B6/D6)	=C6*B6/F6	=D6*F6	=E6*F6
7						=СУММ(F3:F6)	=СУММ (G3:G6)	=СУММ (H3:H6)	=СУММ (I3:I6)
8	F	200
9	L	=G7+1/2*H7

---

В таблице 4.8 представлены результаты расчета.
Таблица 4.8 - Результаты расчета

	А	В	С	D	E	F	G	H	I
2	I	vi	Ki	si	fi	qi*
3	1	10	100	0,1	10	141,42	7,0711	14,142	1414,2
4	2	20	50	0,2	5	100	10	20	500
5	3	5	90	0,2	7	67,082	6,7082	13,416	469,57
6	4	10	20	0,1	5	63,246	3,1623	6,3246	316,23
7						371,75	26,942	53,883	2700
8	F	200
9	L	53,883

---

2 Раздельная оптимизация с ограничением на складские площади

Так как количество необходимых складских площадей (2700 м²) значительно превышает имеющуюся площадь склада (200 м²), поэтому ограничение на складские площади является существенным. В связи с этим скорректируем размеры партии заказов. Для этого составим оптимизационную модель. Цель – минимизировать суммарные расходы при ограничении величины складских площадей.

Получили задачу нелинейной оптимизации, которую можно решить средствами Excel. Для расчетов исходную таблицу копируем в ячейки А11:I18. В столбце q_i* ставим значения, равные 1, для того, чтобы начальные значения удовлетворяли области ограничений.

Столбцом значений будет столбец q_i*. Значения целевой функции находится в ячейке L. Правая часть ограничения записывается в отдельную ячейку. В программе Поиск решения задаем параметры – «нелинейная модель», «неотрицательные значения» (рисунок 4.1).

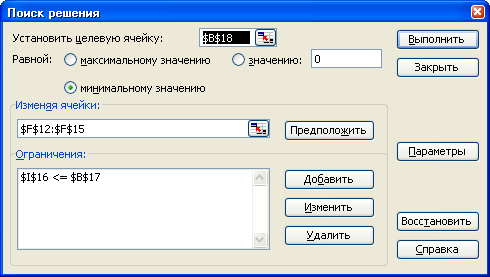
Рисунок 4.1 – Задание условий задачи в программе Поиск решения
Результаты расчетов представлены в таблице 4.9.
Таблица 4.9 - Результаты расчетов

	А	В	С	D	E	F	G	H	I
11	I	vi	Ki	si	fi	qi*
12	1	10	100	0,1	10	7,7538	128,9691	0,77538	77,538
13	2	20	50	0,2	5	10,9164	91,60513	2,18328	54,5821
14	3	5	90	0,2	7	6,19958	72,58561	1,23992	43,397
15	4	10	20	0,1	5	4,89658	40,84482	0,48966	24,4829
16						29,7664	334,0046	4,68824	200
17	F	200
18	L	336,349

---

3 Полное совмещение заказов без учета ограничений на складские площади

Издержки размещения заказа равны
, (4.8)

где - среднее значение издержек (в Excel рассчитывается с помощью функции СРЗНАЧ).

Рассчитаем ₀ и q_i0 без учета ограничений по следующим формулам:

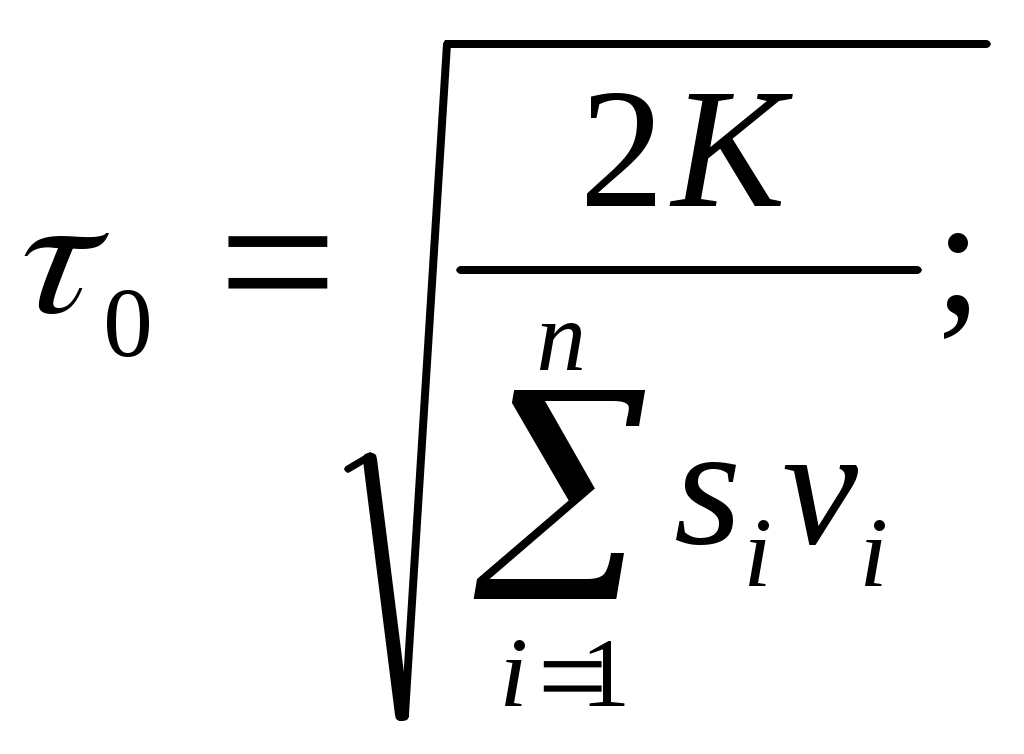(4.9)

. (4.10)

Среднегодовые издержки рассчитаем по формуле
. (4.11)
Проверим существенность ограничений на складские площади при полном совмещении заказов . Ограничение является существенным, поэтому для нахождения оптимального периода возобновления поставок воспользуемся формулами:

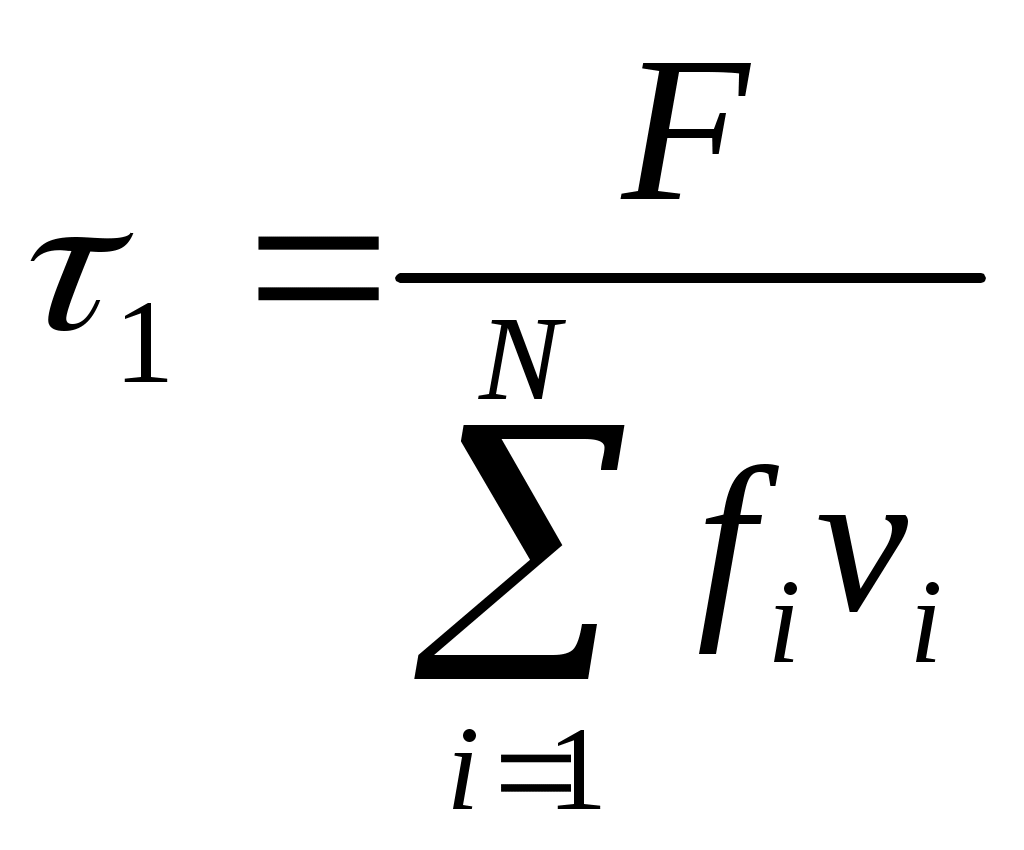; (4.12)

* = min(₀, ₁). (4.13)
Оптимальные поставки определяем по формуле
. (4.14)
Издержки работы системы при условии ограниченности складских помещений рассчитываем по формуле

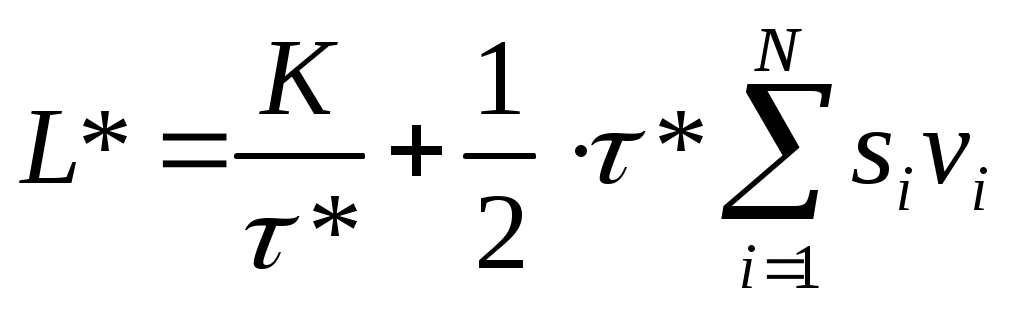. (4.15)
Результаты расчетов представлены в таблице 4.10.
Таблица 4.10 - Результаты расчетов

	А	В	С	D	E	F	G	H	I	J	K	L
20	I	vi	Ki	si	fi	qi0						q*
21	1	10	100	0,1	10	54,51	18,34	5,45	545,11	1	100	7,02
22	2	20	50	0,2	5	109,02	9,17	21,80	545,11	4	100	14,04
23	3	5	90	0,2	7	27,26	16,51	5,45	190,79	1	35	3,51
24	4	10	20	0,1	5	54,51	3,67	5,45	272,55	1	50	7,02
25			260			245,3	47,70	38,16	1553,56	7	285
26	F	200	0	5,451
27	L	38,158	1	0,702
28	Кср	65	*	0,702
29	К	104	L*	150,656

---

4 Действующая система поставок – один раз в квартал с индивидуальным подходом к каждому продукту (без учета ограничений на складские площади)

Так как поставки поквартальные, то .

Издержки рассчитываются по формуле

. (4.16)
Расчеты проводим в таблице 4.11.
Таблица 4.11 - Результаты расчетов

	А	В	С	D	E	F	G	H	I
31	I	vi	Ki	si	fi	qi0
32	1	10	100	0,1	10	2,5	400	0,031	25
33	2	20	50	0,2	5	5	200	0,125	25
34	3	5	90	0,2	7	1,25	360	0,031	8,75
35	4	10	20	0,1	5	2,5	80	0,031	12,5
36							1040	0,219	71,25
37	L	1040,219

---