Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 822
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Модель общей задачи линейного программирования
2 Транспортные задачи в моделировании
3 Экономико-статистическое моделирование и прогнозирование средствами MS Excel
4 Модели управления товарными запасами
5 Системы массового обслуживания
6 Модели сетевого планирования и управления
7 Применение элементов теории игр при принятии управленческих решений
Для содержания запасов продукции понадобятся складские площади в размере 71,25 м2. Издержки работы системы составят 1040,219 ден. ед.
5 Анализ полученных результатов
Сведем полученные результаты в таблицу 4.12.
Таблица 4.12 – Анализ работы каждой из систем управления запасами
| Результаты системы | Необходимые складские площади, м2 | Издержки работы системы, ден. ед./год |
| Действующая система | 71,25 | 1040,219 |
| Раздельное управление поставками | 2700 | 53,883 |
| Управление поставками при полном совмещении заказов | 1553,56 | 38,158 |
| Раздельное управление поставками с ограничениями на складские площади | 200 | 336,349 |
| Управление поставками при полном совмещении заказов и ограничении на складские площади | 200 | 150,656 |
Задача для самостоятельного решения (по вариантам)
Склад оптовой торговли отпускает пять видов товаров (таблица 4.13). Заданы потребности vi, т/г., издержки заказывания Кi, ден. ед., издержки содержания тонны в год si, ден. ед., расход складской площади на единицу товара fi, м2. Известна общая величина складской площади торгового зала F.
Требуется:
1) определить оптимальные партии поставок при ограничении максимального уровня запаса. Учесть, что все пять видов продукции поступают на склад от разных поставщиков (раздельная оптимизация);
2) если продукция поступает из одного источника (полное совмещение заказов), издержки размещения заказов в этом случае равны средним издержкам индивидуальных издержек заказывания
3) сравнить полученные результаты с действующей системой поставок — один раз в квартал с индивидуальным подходом к каждому продукту без учета ограничений на складские площади;
4) оценить работу каждой из систем управления запасами, выбрать наиболее эффективную и обосновать полученное решение.
Таблица 4.13 – Исходные данные для решения задачи
-
Вариант
F
I
1
2
3
4
5
1
1200
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
900
10
5
16
700
5
15
4
300
20
10
15
1000
30
2
22
200
6
3
10
2
500
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
400
10
16
4
600
12
8
3
800
11
8
5
700
9
7
4
200
8
4
4
3
500
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
700
5
15
20
200
5
4
5
500
20
10
2
150
3
2
8
800
4
20
4
4
1500
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
3000
4
40
4
5000
6
6
3
6400
7
14
5
1500
6
6
40
80
4
16
20
5
900
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
900
5
4
8
400
10
7
5
800
11
6
6
200
7
4
3
150
2
2
3
6
800
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
4000
10
8
3
2000
7
70
2
8000
15
6
2
600
110
8
5
1500
6
20
30
7
1350
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
5000
6
15
10
7000 110
8
5
2000
7
20
2
200
5
4
3
800
4
8
4
Продолжение таблицы 4.13
-
Вариант
F
I
1
2
3
4
5
8
1000
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
48000 120
200
1,8
22400 160
280
1,6
6400
130
260
1,2
8600
140
200
1,5
2460
110
250
1,4
9
1250
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
3200
110
150
14
2100 150
260
5
5400 120
240
3
7900 130
200
4
2420 100
230
6
10
6000
I, т/г.
Ki, ден. ед.
si, ден. ед./ т в год
fi, м2
1350
70
11
8
1210
65
9
9
1150
80
3
4
1300
77
7
6
890
93
6
7
5 Системы массового обслуживания
-
Формируемые навыки и умения:
- освоение методики построения систем массового обслуживания;
- освоение методики расчета основных характеристик задач массового обслуживания.
Теоретическая поддержка
Системы массового обслуживания (СМО) представляют собой структуры, содержащие одно или несколько обслуживающих устройств (каналов), на вход которых в случайные моменты времени поступают требования для обслуживания. СМО включаетследующиеэлементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (канал обслуживания), выходящий поток требований (обслуженных заявок).
СМО является предметом изучения теории массового обслуживания. Целью теории массового обслуживания является выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО. Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.
СМО играют важную роль во многих областях экономики, финансов, производства и быта. В качествепримеров СМО в финансово-экономической сфере можно привести системы, представляющие собой: банки различных типов, страховые организации, налоговые инспекции, аудиторские службы, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы).
Для торговой деятельности характерны массовое поступление товаров, денег, массовое обслуживание покупателей и т. п. В торговле возникают задачи анализа работы, например торгового отдела, торгового предприятия или секции, для оценки их деятельности, выявления недостатков, резервов и принятия в конечном итоге мер, направленных на увеличение ее эффективности. Кроме того, возникают задачи, связанные с созданием и внедрением более экономичных способов выполнения операций в пределах секции, отдела, торгового предприятия, овощной базы, управления торговли и т. п. В организации торговли методы теории массового обслуживания позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры.
Другим характерным примером СМО могут служить склады или базы снабженческо-сбытовых организаций, и задача теории массового обслуживания сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку – как требование.
1 Одноканальная СМО с ожиданием и ограничением на длину очереди
Рассмотрим СМО с одним каналом (n=1), на вход которой поступает простейший поток заявок с интенсивностью λ. Предположим, что поток обслуживаний также простейший с интенсивностью μ. Это означает, что непрерывно занятый канал обслуживает в среднем μ заявок в единицу времени. Заявка, поступившая в СМО в момент, когда канал занят, не покидает систему, а становится в очередь и ожидает обслуживания.
В данной системе имеется ограничение на длину очереди, под которой понимается максимальное число мест в очереди, а именно в очереди могут находиться максимум m> 1 заявок. Поэтому заявка, пришедшая на вход СМО, в момент, когда в очереди уже стоят m заявок, получает отказ и покидает систему необслуженной.
В таблице 5.1 сведены предельные характеристики СМО.
Таблица 5.1 – Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием и ограничением на длину очереди
| № | Предельные характеристики | Обозначения, формулы |
| 1 | Показатель нагрузки (трафик) СМО | |
| 2 | Вероятности состояний СМО,выраженные через показатель нагрузки ρ | 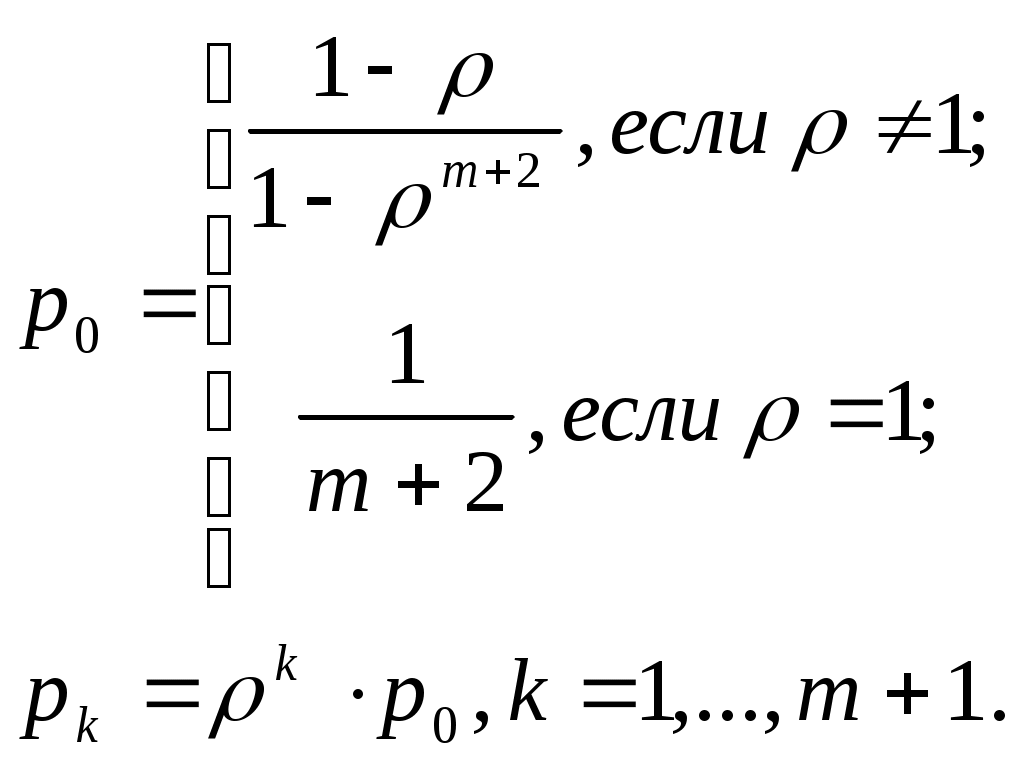 |