Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 840
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Модель общей задачи линейного программирования
2 Транспортные задачи в моделировании
3 Экономико-статистическое моделирование и прогнозирование средствами MS Excel
4 Модели управления товарными запасами
5 Системы массового обслуживания
6 Модели сетевого планирования и управления
7 Применение элементов теории игр при принятии управленческих решений
Продолжение таблицы 5.1
Пример решения задачи
Постановка задачи. На складе бакалейных товаров имеется одна погрузочно-разгрузочная рампа. Площадка при складе, на которой машины ожидают загрузку, может вместить не более трех машин одновременно, и если она занята, то очередная машина, прибывшая к складу, в очередь не становится, а проезжает на другой склад. В среднем машины прибывают на склад каждые 2 мин. Процесс загрузки одной машины продолжается в среднем 2,5 мин.
Определить:
Решение задачи
Математической моделью данного склада является одноканальная СМО с ожиданием и ограничением на длину очереди (m=3). Предполагается, что поток машин, подъезжающих к складу для загрузки, и поток обслуживаний – простейшие.
Поскольку машины прибывают в среднем через каждые 2 мин, то интенсивность входящего потока равна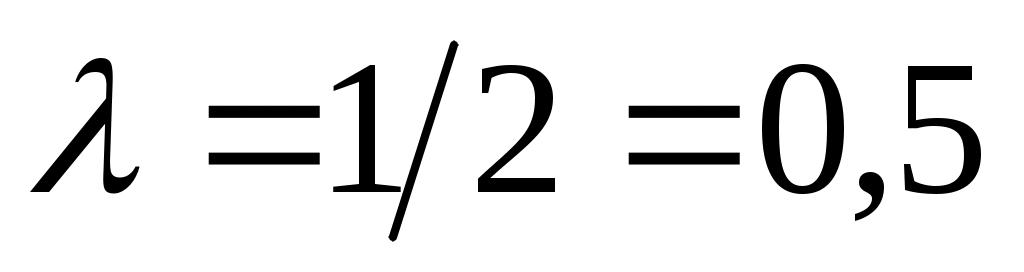 (машин в минуту). Среднее время обслуживания одной машины
(машин в минуту). Среднее время обслуживания одной машины 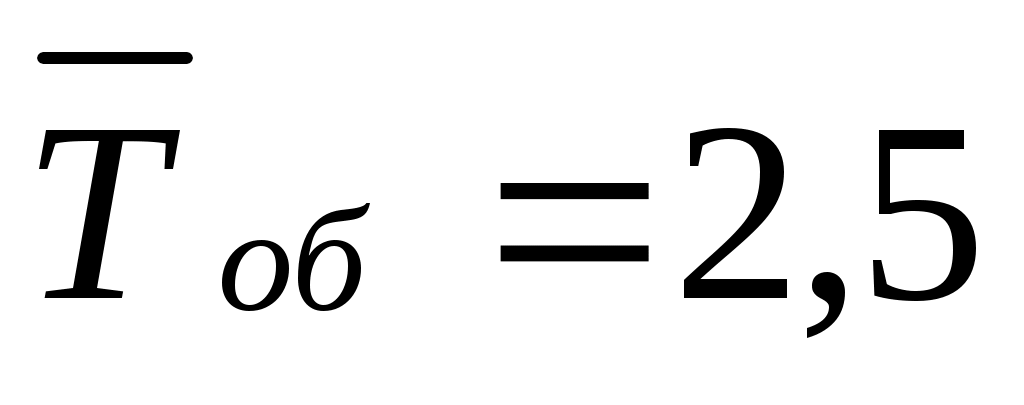 мин, следовательно, интенсивность потока обслуживаний
мин, следовательно, интенсивность потока обслуживаний 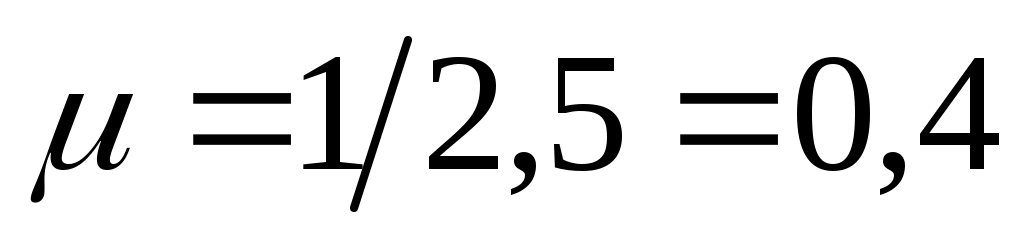 (машины в минуту).
(машины в минуту).
Определяем показатель нагрузки СМО:
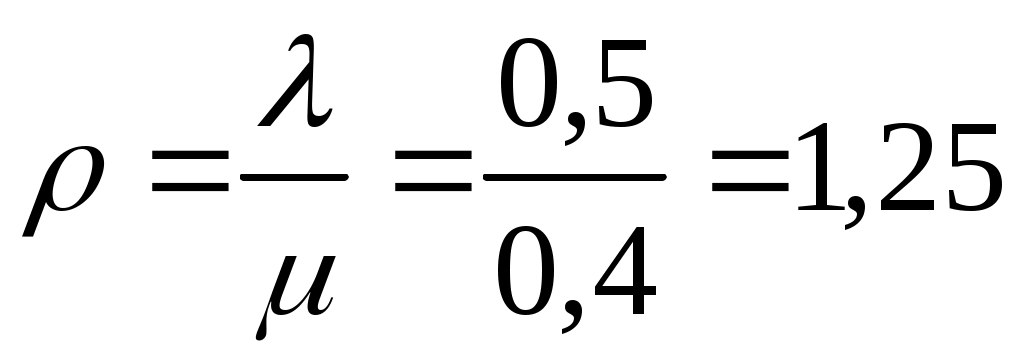 .
.
По формуле из 4-й строки таблицы 5.1 определяем вероятность отказа:
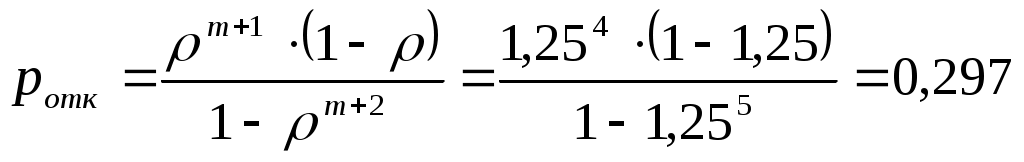 .
.
По формуле из 6-й строки таблицы 5.1 относительная пропускная способность составит
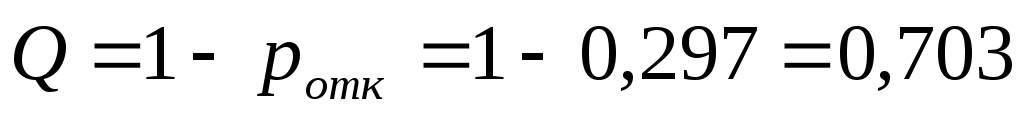 .
.
По формуле из 7-й строки таблицы 5.1 абсолютная пропускная способность составит
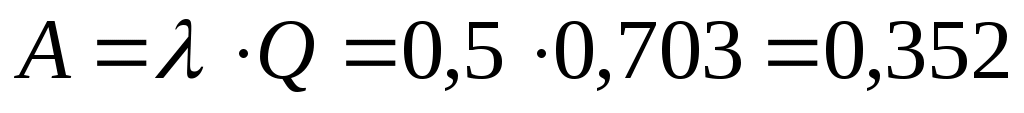 .
.
Среднее число машин, ожидающих в очереди на загрузку (9-я строка таблицы 5.1):
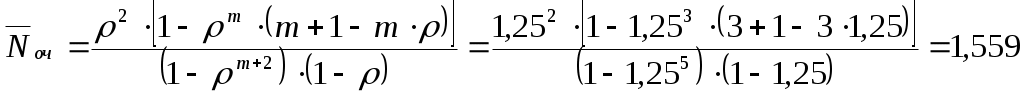 .
.
Среднее число машин под обслуживанием (10-я строка таблицы 5.1):
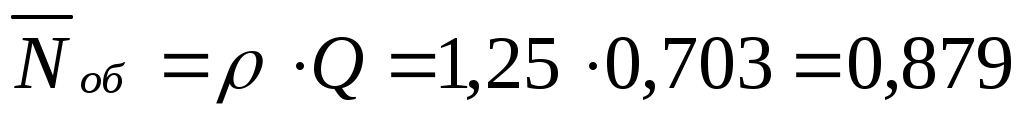 .
.
Среднее число машин, связанных со складом (находящихся в системе), см. формулу в 11-й строке таблицы 5.1:
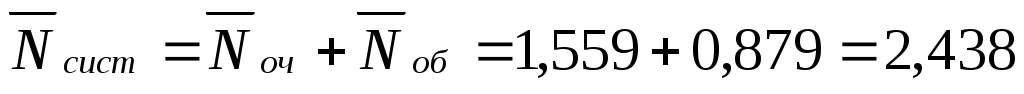 .
.
Среднее время ожидания машины в очереди (формула в 12-й строке таблицы 5.1):
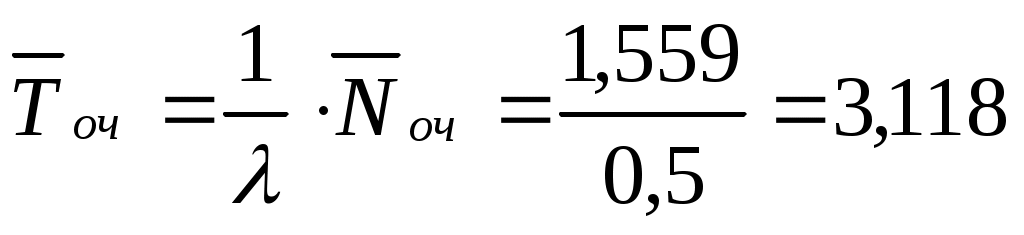 .
.
Среднее время, проведенное машиной на складе (см. формулу в 13-й строке таблицы 5.1):
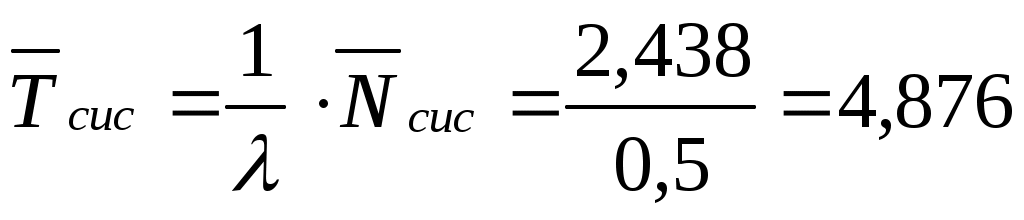 .
.
Среднее время обслуживания одной машины, относящееся ко всем машинам – обслуженным и необслуженным (см. формулу в 15-й строке таблицы 5.1):
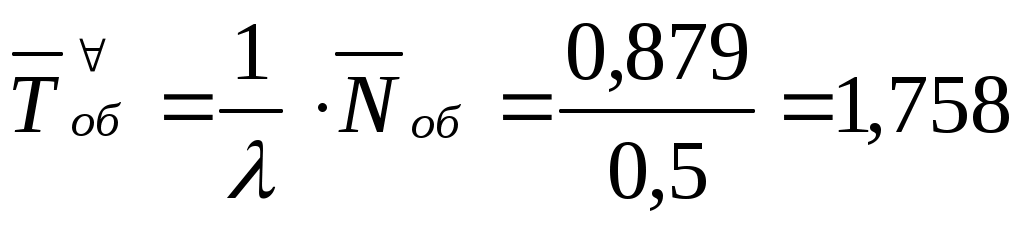 .
.
Таким образом, из анализа работы СМО следует, что из каждых 100 подъезжающих машин 30 получают отказ (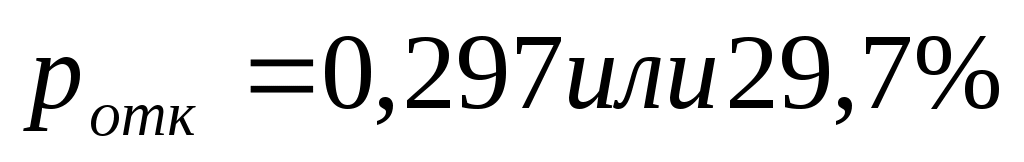 ), т.е. обслуживается 2/3 заявок. Поэтому необходимо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число погрузочно-разгрузочных рамп, либо увеличить площадку для ожидания. Оптимальное решение принимается с учетом затрат, связанных соответственно с увеличением штата обслуживающего персонала (увеличение производительности канала), с расширением площадки для ожидания или проектирования дополнительной рампы, и потерь, связанных с потерей заявок на обслуживание.
), т.е. обслуживается 2/3 заявок. Поэтому необходимо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число погрузочно-разгрузочных рамп, либо увеличить площадку для ожидания. Оптимальное решение принимается с учетом затрат, связанных соответственно с увеличением штата обслуживающего персонала (увеличение производительности канала), с расширением площадки для ожидания или проектирования дополнительной рампы, и потерь, связанных с потерей заявок на обслуживание.
2 Одноканальная СМО с ожиданием
Проанализируем работу одноканальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. Предполагаем, что входящий поток с интенсивностью λ и поток обслуживаний с интенсивностью μ простейшие. Длина очереди в данной СМО бесконечна, т.е. m → ∞. При условии, что λ < μ, т.е. ρ < 1, с течением времени устанавливается предельный режим и предельные вероятности состояний СМО существуют.
Характеристики данной СМО представлены в таблице 5.2.
Таблица 5.2–Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием
Продолжение таблицы 5.2
3 Многоканальная СМО с отказами
Если требование поступает в систему в момент, когда все n каналов заняты, то оно получает отказ (покидает систему необслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца.
Характеристики эффективности СМО с отказами представлены в таблице 5.3.
Таблица 5.3 – Предельные характеристики эффективности функционирования многоканальной СМО с отказами
Продолжение таблицы 5.3
Пример решения задачи
Постановка задачи. На вокзале, в кафе быстрого обслуживания имеется 3 столика. Если клиент заходит в кафе, когда все столы заняты, то он уходит из кафе, не ожидая обслуживания. Среднее число клиентов, обращающихся в кафе за 1 час, равно 20. Среднее время, в течение которого столик кафе занят другим клиентом составляет 6 мин.
На вокзале, в мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской, не ожидая обслуживания. Среднее число клиентов, обращающихся в мастерскую за 1 час, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин.
Определить основные характеристики эффективности функционирования данного кафе в предельном режиме:
| № | Предельные характеристики | Обозначения, формулы |
| 3 | Вероятности состояний СМО, выраженные через средний интервал времени | 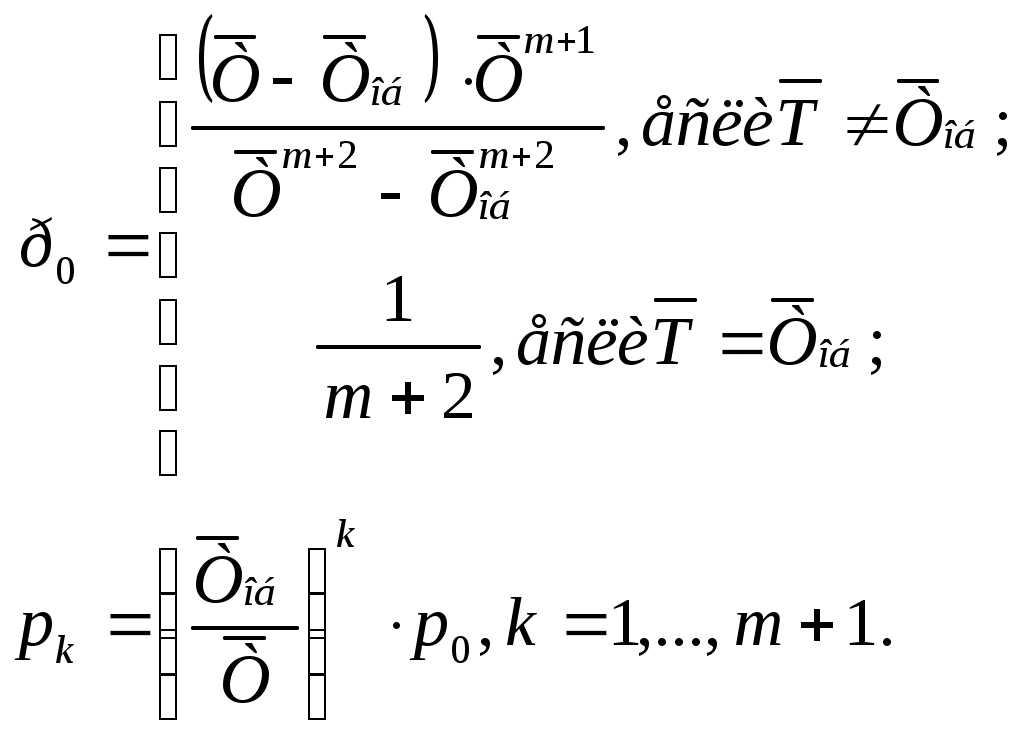 |
| 4 | Вероятность отказа | 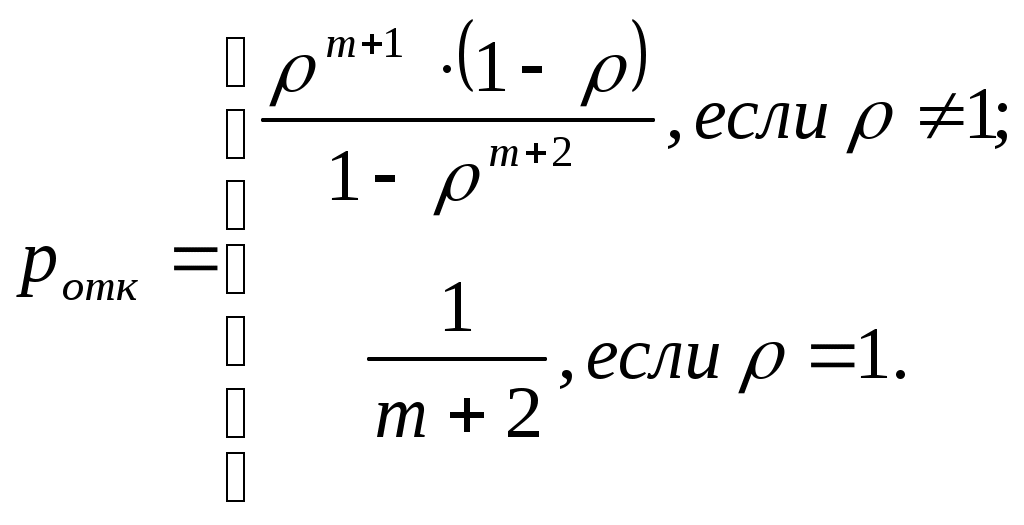 |
| 5 | Вероятность того, что заявка будет принята в систему (не получит отказ) | |
| 6 | Относительная пропускная способность | |
| 7 | Абсолютная пропускная способность | |
| 8 | Интенсивность выходящего потока обслуженных заявок | |
| 9 | Среднее число заявок в очереди | 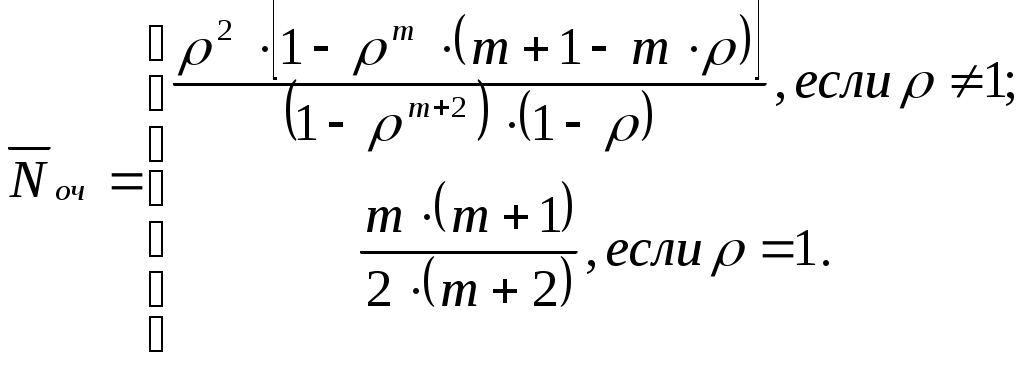 |
| 10 | Среднее число заявок, находящихся под обслуживанием | |
| 11 | Среднее число заявок, находящихся в системе (как в очереди, так и под обслуживанием) | |
| 12 | Среднее время ожидания заявки в очереди | |
| 13 | Среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием) | |
| 14 | Среднее время обслуживания одной заявки, относящееся только к обслуженным заявкам | |
| 15 | Среднее время обслуживания одной заявки, относящееся ко всем заявкам, как обслуженным, так и получившим отказ | |
Пример решения задачи
Постановка задачи. На складе бакалейных товаров имеется одна погрузочно-разгрузочная рампа. Площадка при складе, на которой машины ожидают загрузку, может вместить не более трех машин одновременно, и если она занята, то очередная машина, прибывшая к складу, в очередь не становится, а проезжает на другой склад. В среднем машины прибывают на склад каждые 2 мин. Процесс загрузки одной машины продолжается в среднем 2,5 мин.
Определить:
-
вероятность отказа; -
относительную и абсолютную пропускные способности СМО; -
среднее число машин ожидающих загрузки; -
среднее время ожидания машины в очереди; -
среднее время пребывания машины на складе (включая обслуживание).
Решение задачи
Математической моделью данного склада является одноканальная СМО с ожиданием и ограничением на длину очереди (m=3). Предполагается, что поток машин, подъезжающих к складу для загрузки, и поток обслуживаний – простейшие.
Поскольку машины прибывают в среднем через каждые 2 мин, то интенсивность входящего потока равна
Определяем показатель нагрузки СМО:
По формуле из 4-й строки таблицы 5.1 определяем вероятность отказа:
По формуле из 6-й строки таблицы 5.1 относительная пропускная способность составит
По формуле из 7-й строки таблицы 5.1 абсолютная пропускная способность составит
Среднее число машин, ожидающих в очереди на загрузку (9-я строка таблицы 5.1):
Среднее число машин под обслуживанием (10-я строка таблицы 5.1):
Среднее число машин, связанных со складом (находящихся в системе), см. формулу в 11-й строке таблицы 5.1:
Среднее время ожидания машины в очереди (формула в 12-й строке таблицы 5.1):
Среднее время, проведенное машиной на складе (см. формулу в 13-й строке таблицы 5.1):
Среднее время обслуживания одной машины, относящееся ко всем машинам – обслуженным и необслуженным (см. формулу в 15-й строке таблицы 5.1):
Таким образом, из анализа работы СМО следует, что из каждых 100 подъезжающих машин 30 получают отказ (
2 Одноканальная СМО с ожиданием
Проанализируем работу одноканальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. Предполагаем, что входящий поток с интенсивностью λ и поток обслуживаний с интенсивностью μ простейшие. Длина очереди в данной СМО бесконечна, т.е. m → ∞. При условии, что λ < μ, т.е. ρ < 1, с течением времени устанавливается предельный режим и предельные вероятности состояний СМО существуют.
Характеристики данной СМО представлены в таблице 5.2.
Таблица 5.2–Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием
| № | Предельные характеристики | Обозначения, формулы |
| 1 | Среднее время обслуживания одной заявки | |
| 2 | Показатель нагрузки (трафик) СМО | |
| 3 | Вероятности состояний СМО | |
| 4 | Вероятность отказа | |
| 5 | Вероятность того, что заявка будет принята в систему | |
| 6 | Относительная пропускная способность | |
| 7 | Абсолютная пропускная способность | |
| 8 | Интенсивность выходящего потока заявок | |
| 9 | Среднее число заявок в очереди | |
Продолжение таблицы 5.2
| № | Предельные характеристики | Обозначения, формулы |
| 10 | Среднее число заявок, находящихся под обслуживанием | |
| 11 | Среднее число заявок, находящихся в системе (как в очереди, так и под обслуживанием) | |
| 12 | Среднее время ожидания заявки в очереди | |
| 13 | Среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием) | |
3 Многоканальная СМО с отказами
Если требование поступает в систему в момент, когда все n каналов заняты, то оно получает отказ (покидает систему необслуженным). Если же в момент поступления требования имеется хотя бы один свободный канал, то оно принимается к обслуживанию и обслуживается до конца.
Характеристики эффективности СМО с отказами представлены в таблице 5.3.
Таблица 5.3 – Предельные характеристики эффективности функционирования многоканальной СМО с отказами
| № | Предельные характеристики | Обозначения, формулы |
| 1 | Вероятности состояний СМО рk, k = 1, …, n, выраженные через интенсивность входящего потока λ и интенсивность потока обслуживания μ | 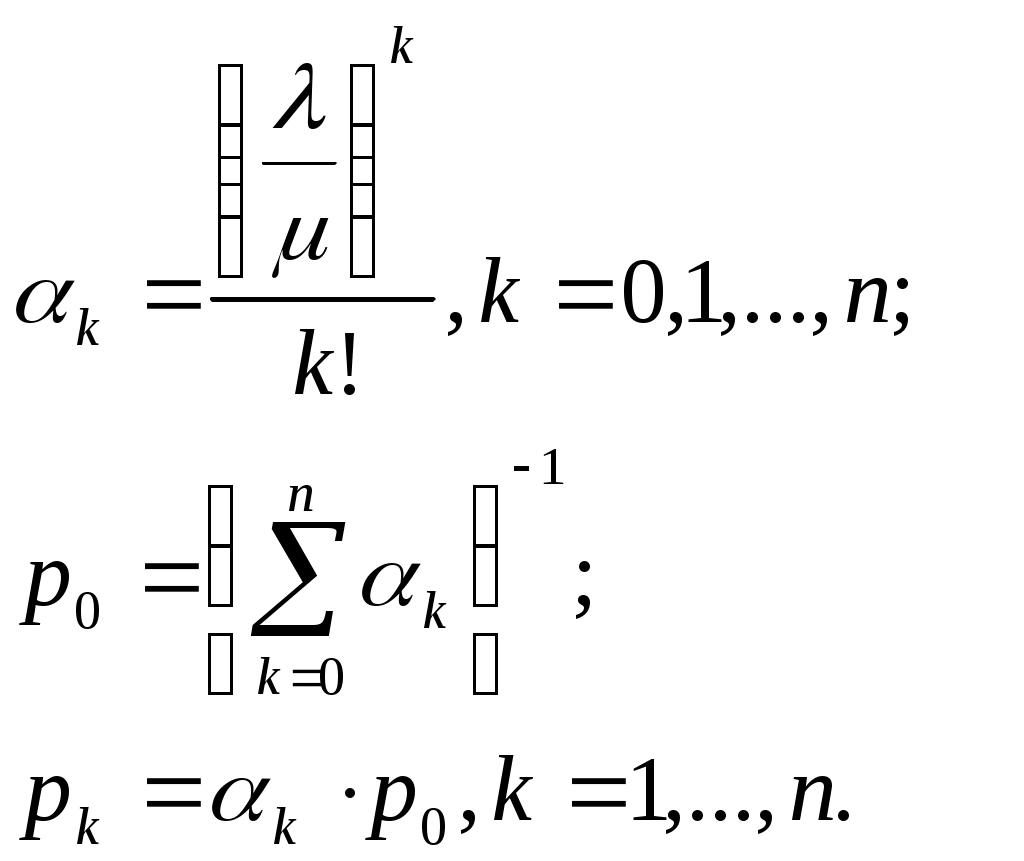 |
| 2 | Приведенная интенсивность входящего потока – трафик (показатель нагрузки СМО) | где |
| 3 | Вероятности состояний СМО рk, k = 1, …, n, выраженные через трафик ρ | 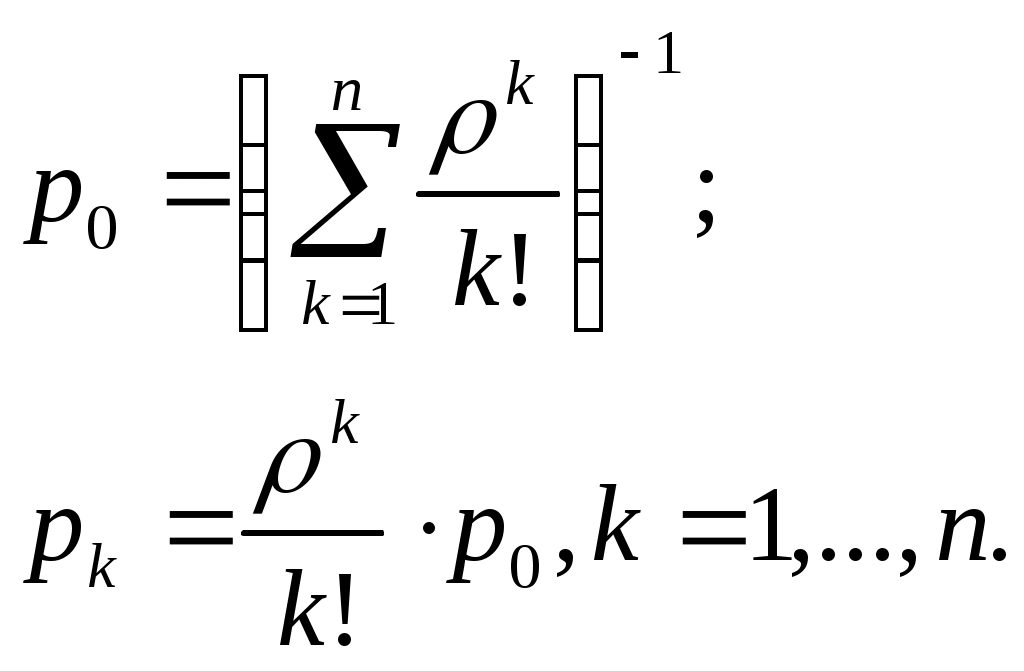 |
| 4 | Вероятность отказа ротк | |
Продолжение таблицы 5.3
| № | Предельные характеристики | Обозначения, формулы |
| 5 | Вероятность того, что пришедшая заявка будет обслужена | |
| 6 | Относительная пропускная способность | |
| 7 | Абсолютная пропускная способность | |
| 8 | Интенсивность выходящего потока обслуженных заявок | |
| 9 | Среднее число занятых каналов | |
| 10 | Среднее время пребывания заявки в СМО (формула Литтла) | |
Пример решения задачи
Постановка задачи. На вокзале, в кафе быстрого обслуживания имеется 3 столика. Если клиент заходит в кафе, когда все столы заняты, то он уходит из кафе, не ожидая обслуживания. Среднее число клиентов, обращающихся в кафе за 1 час, равно 20. Среднее время, в течение которого столик кафе занят другим клиентом составляет 6 мин.
На вокзале, в мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской, не ожидая обслуживания. Среднее число клиентов, обращающихся в мастерскую за 1 час, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин.
Определить основные характеристики эффективности функционирования данного кафе в предельном режиме:
-
вероятность того, что клиент получит отказ ротк; -
вероятность того, что клиент будет обслужен роб; -
среднее число клиентов А, обслуживаемых кафе в течение 1 часа; -
среднее число занятых столов .
.