Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Решение задачи
Данное кафе может рассматриваться как многоканальная СМО с отказами, поскольку клиентам на вокзале некогда ожидать обслуживания в очереди, и если все столы заняты ранее пришедшими клиентами, то вновь прибывший клиент покидает кафе необслуженным. Параметры системы: n = 3, λ = 20 (чел./ч), μ = 1 / Т_об = 1/6 (чел./мин), ρ = λ / μ = 20/10 = 2 (эрланга).

Вычисление предельных вероятностей состояний системы удобно проводить в таблице 5.4.

Сначала производим вычисления в столбце 2 по формуле (k - число занятых каналов), которая следует из формулы в 3-й строке таблицы 5.3. Вычисляется сумма всех элементов столбца 2: ∑ = 6,333. Вероятность того, что все столы свободны р₀ = 1/6,333 = 0,158 (см. формулу в 3-й строке таблицы 5.3). Предельные вероятности р_k (столбец 3) вычисляются умножением элементов столбца 2 на вероятность р₀. Сумма эле­ментов столбца 3 должна быть равна 1+Δ, где Δ — ошибка округления.

Таблица 5.4 – Расчет предельных вероятностей состояний системы

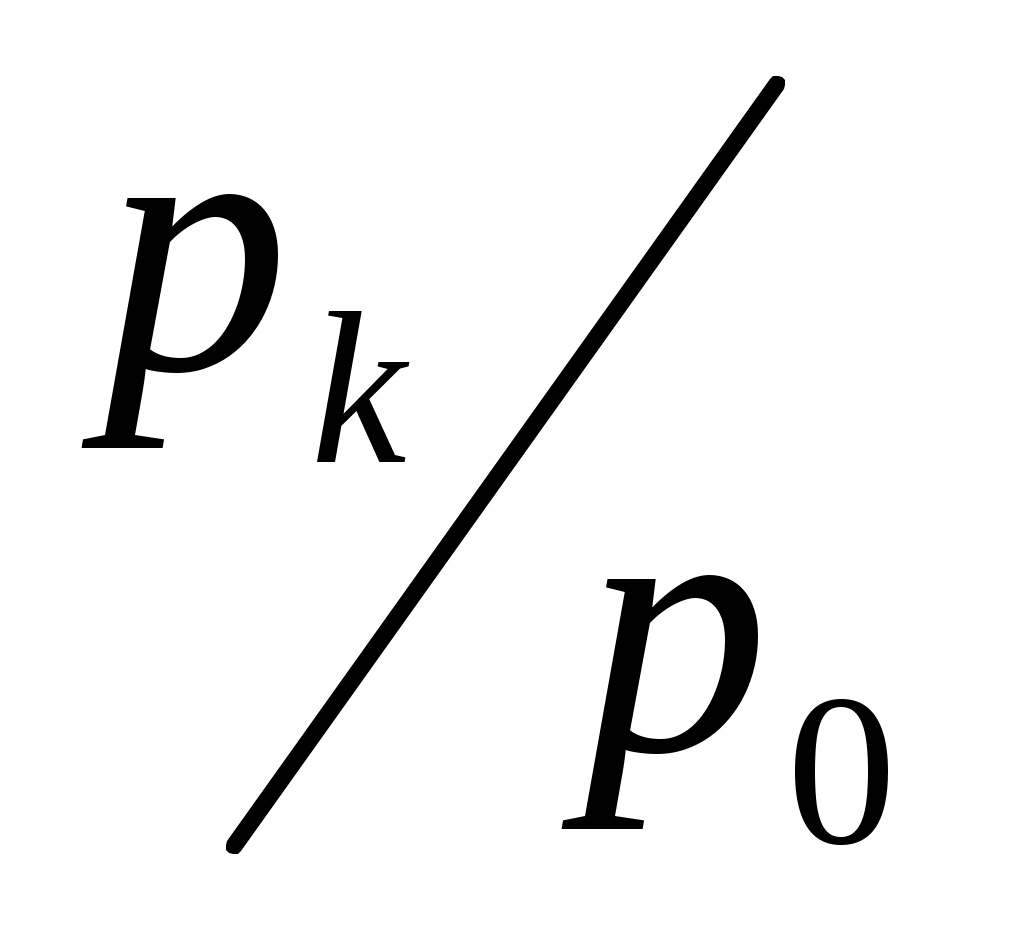
Значения случайной величины k (число занятых столов)		рk	kpk
1	2	3	4
0	1,000	0,158	0
1	2,000	0,316	0,316
2	2,000	0,316	0,632
3	1,333	0,211	0,633
∑	6,333	1,001	1,581

Значения элементов столбца 4 получаются умножением эле­ментов столбца 1 на соответствующие элементы столбца 3. Сумма элементов столбца 4 равна среднему числу занятых каналов (см. 9-ю строку таблицы 5.3).

Вероятность того, что клиент получит отказ, равна вероятно­сти того, что заняты все три столика, т.е.

---

р₃ = 0,211 (см. 4-ю стро­ку таблицы 5.3).

Вероятность того, что клиент будет обслужен (относительная пропускная способность кафе), определяется по формуле (см. 6-ю строку таблицы 5.3) , т.е. из 100 клиентов, обращающихся в кафе, в среднем 79 клиентов будут обслужены и 21 – получит отказ.

Абсолютная пропускная способность кафе, т.е. среднее число клиентов, обслуживаемых в единицу времени, (см. 7-ю строку таблицу 5.3) составляет

.
4 Многоканальная СМО с ожиданием и ограничением на длину очереди
Пусть в n-канальную систему массового обслуживания поступает простейший поток требований с интенсивностью λ; число мест в очереди ограничено и равно m. Время обслуживания требований (для одного канала) экспоненциальное, со средним значением .
Таблица 5.5 – Характеристики функционирования многоканальной СМО с ожиданием и ограничением на длину очереди

№	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) нагрузки СМО (трафик)	.
2	Показатель (коэффициент) нагрузки, приходящийся на один канал
3	Вероятность того, что все каналы свободны (вероятность простаивания всей системы)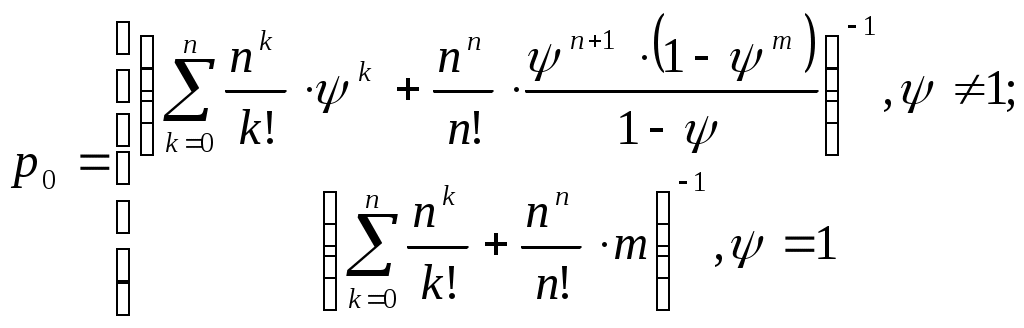

Продолжение таблицы 5.5

№	Предельные характеристики	Обозначения, формулы
4	Вероятности состояний СМО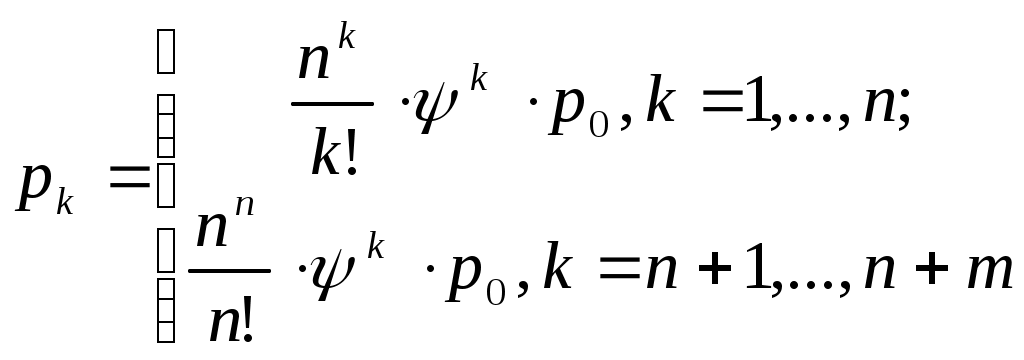
5	Вероятность отказа заявке
6	Вероятность того, что заявка будет принята в СМО
7	Относительная пропускная способность
8	Абсолютная пропускная способность
9	Среднее число занятых каналов (т.е. среднее число заявок, находящихся под обслуживанием)
10	Среднее число заявок, находящихся в очереди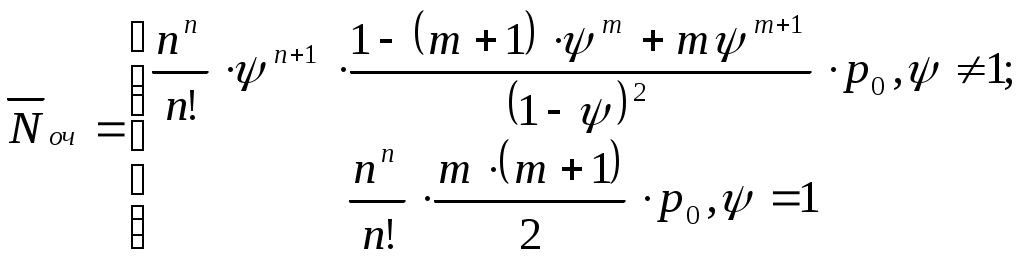
11	Среднее число заявок, находящихся в СМО (как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе
14	Среднее время обслуживания одной заявки, относящееся ко всем заявкам, как обслуженным, так и получившим отказ

---

5 Многоканальная СМО с неограниченной длиной очере­ди
Рассмотрим СМО, состоящую из n ≥ 1 каналов обслуживания, с ожиданием и без ограничения на длину очереди. Заявка, поступившая в СМО в момент, когда все n каналов заняты, становится в очередь и ожидает своего обслуживания. Любая пришедшая заявка будет обслужена. Поток заявок и поток обслуживаний каждым каналом – простейшие с интенсивностью соответственно λ и μ.

Таблица 5.6 – Характеристики функционирования многоканальной СМО с ожиданием

№	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) нагрузки СМО (трафик)
2	Показатель (коэффициент) нагрузки, приходящийся на один канал
3	Вероятность того, что все каналы свободны (вероятность простаивания всей системы)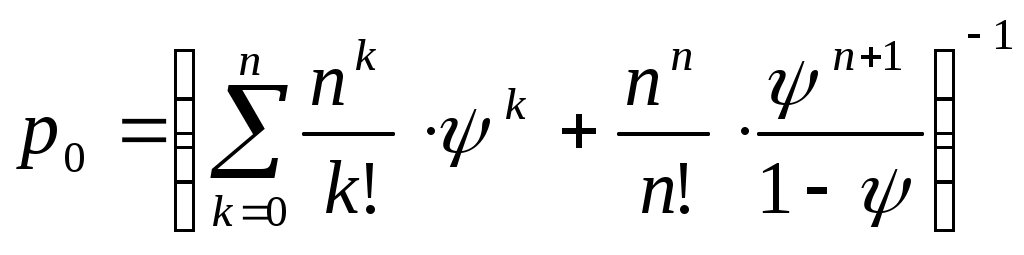
4	Вероятности состояний СМО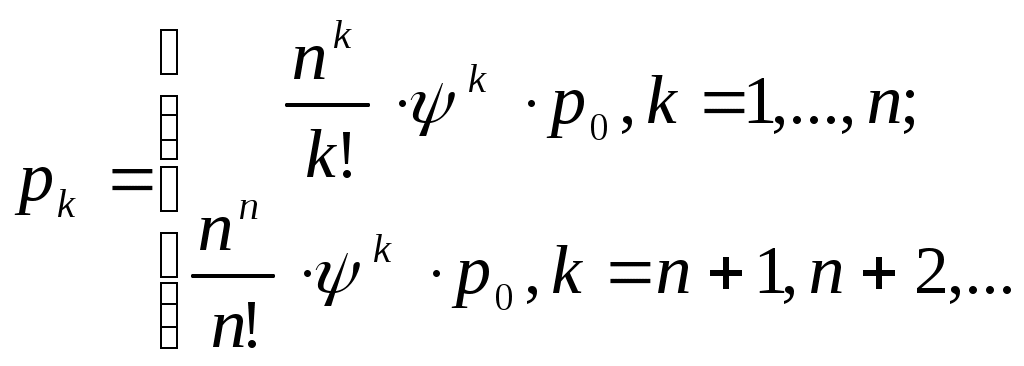
5	Вероятность отказа заявке
6	Вероятность того, что заявка будет принята в СМО
7	Относительная пропускная способность
8	Абсолютная пропускная способность
9	Среднее число занятых каналов (т.е. среднее число заявок, находящихся под обслуживанием)
10	Среднее число заявок, находящихся в очереди
11	Среднее число заявок, находящихся в СМО (как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе
14	Среднее время обслуживания одной заявки, относящееся ко всем заявкам, как обслуженным, так и получившим отказ

---

Пример решения задачи
Постановка задачи. Пусть рампа супермаркета по приему товара оборудована тремя раз­грузочными площадками, каждая из которых одномоментно может об­служивать только один автомобиль, прибывший от любого из трех опто­вых поставщиков. Автомобили с товаром прибывают в случайные мо­менты времени, поскольку усилия менеджера по регуляризации поста­вок успеха пока что не имели. Установить какой-либо график прибытия автомобилей не удается, и поэтому приходится мириться со стихией слу­чайности, но действовать при этом по возможности оптимально.

Интенсивность поступления товара от каждого из поставщиков при­мерно одинакова, и прибытие автомобилей от каждого из них происходит в среднем через каждый 1,5 часа, так что суммарно на разгрузку прибыва­ет в среднем два автомобиля в течение часа, каждый из которых либо разгружается немедленно на любой из свободных площадок, либо ожида­ет разгрузки до освобождения одной из них. Среднее время, затрачивае­мое на обслуживание одного автомобиля, составляет 84 мин.

Требуется проанализировать работу системы приемки товара и выра­ботать возможные рекомендации по улучшению работы рампы в услови­ях случайности прибытия автомобилей с товаром.
Решение задачи
Запишем представленное в условии задачи описание системы, исполь­зуя введенные ранее обозначения: n = 3;  = 2 (авт./ч); Т_об = 84 мин = 1,4 ч; μ = 1 / Т_об = 1/1,4 = = 0,7143 (авт./ч), ρ = λ / μ = 2/0,7143 = 2,8 (эрланга).

Проверяем выполнение условия существования стационарного ре­жима работы системы:

.

Поскольку найденная величина больше интенсивности входного по­тока заявок (nμ > ), то условие существования финальных вероятнос­тей выполнено.

Показатель нагрузки, приходящийся на один канал, рассчитаем по формуле (см. 2-ю строку таблицы 5.6):

.

Вычислим вероятность свободного состояния СМО р₀=0,016 (см. 3-ю строку таблицы 5.6). Сред­нее число заявок в очереди (см. 10-ю строку таблицы 5.6). Среднее число заявок в системе (см. 11-ю строку таблицы 5.6).

---

Применяя формулы Литтла (см. 12-ю и 13-ю строки таблицы 5.6), находим:

- среднее время ожидания заявки в очереди

- среднее время пребывания заявки в системе .

От поставщиков стали поступать нарекания на то, что время приемки товара неприемлемо велико, и требования закрепления за ними постоян­ного места на рампе с целью рационализации этого процесса.

Фактически эти требования сводятся к разделению трехканальной СМО на три одноканальные с соответствующим разделением входного потока заявок на три равные части. Таким образом, перед нами встает задача анализа одной из таких СМО, поскольку все они одинаковы.

Каждой из трех одноканальных систем после рационализации соот­ветствуют следующие исходные данные: n = 1;  = 2/3 (авт./ч); Т_об = 1,4 ч; μ = 0,7143 (авт./ч), ρ = λ / μ = 0,9333 (эрланга).

Находим: р₀=0,067; ; ; ; .

Сравнивая одноканальную систему с прежней, трехканальной, заме­чаем, что число заявок в очереди увеличилось, хотя и незначительно. Но надо учитывать, что очередь со средней длиной 13,1 устанавливается к каждой из трех площадок. Поэтому в целом на рампе будут ожидать разгрузки в среднем примерно 39,3 заявок, что значительно превышает среднюю длину очереди к трехканальной системе. Это может привести к нарушению работы всего процесса приемки товара. Сильно возросло сред­нее время пребывания автомобиля в системе и стало равно 21 ч.

Учитывая проведенный анализ, приходим к выводу, что задуманная рационализация нецелесообразна. Однако с таким выводом не следует спешить. Не исключено, что поставщики сами займутся регуляризацией поставки товара, например, установив четкое расписание отправки товара, что создаст возможность ритмичной работы бригад по приемке товара. Иначе говоря, в процессе приемки случайности будут исключены, а очере­ди исчезнут. Но если же на регуляризацию потоков заявок рассчитывать не приходится, то трехканальная система сохраняется в неизменном виде.

---