Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

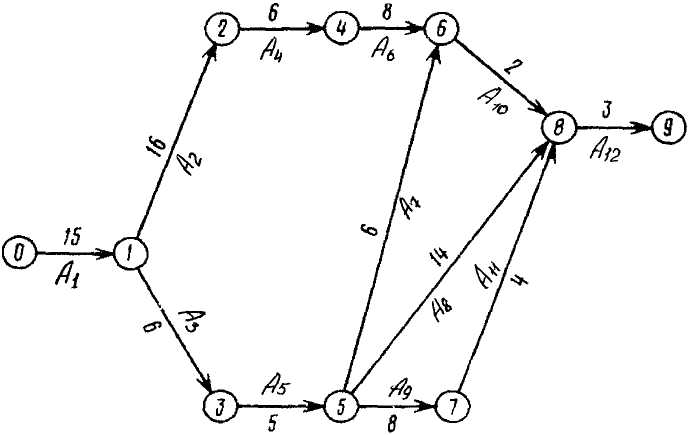
Рисунок 6.1 – Сетевой график работ по переводу магазина на самообслуживание
Расчёт временных параметров сетевого графика включает четыре этапа.

Пер­вый этап называется прямым проходом. Вычисления начинаются с исходного со­бытия и продолжаются, пока не будет достигнуто завершающее событие всей сети. Для каждого события вычисляется число, представляющее ранний срок сверше­ния события по формуле

. (6.1)
На втором этапе, называемом обратным проходом, вычисления на­чинаются с завершающего события и продолжаются до тех пор, пока не будет дос­тигнуто исходное событие. Для каждого события вычисляют поздний срок свер­шения события по формуле
. (6.2)
На третьем этапе рассчитывается резерв времени событий по формуле
R(i) = t_п(i) – t_р(i). (6.3)
На четвёртом этапе определяют критические события, как не имеющие ре­зервов времени, критические работы и критический путь. По результатам расчётов строят сводную таблицу, необходимую для построения календарного графика.

При расчете временных параметров вручную удобно проводить вычисления непос­редственно на графе, воспользовавшись четырехсекторной схе­мой. В этом случае каждый кружок, обозначающий событие, делят на четыре сектора, в каждом из которых записывается соответствующая информация (рисунок 6.2).

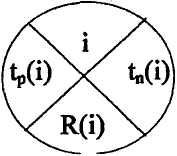
Рисунок 6.2 – Четырех секторная схема
1. Проставляем в верхних секторах номера событий (в со­ответствии с ранжированием).

2. Рассматривая события в порядке возрастания номеров и имея в виду, что t_р(1) = 0, по входящим в это событие работам по формуле (6.1) определяем t_р(j) и записываем в левом секторе.

3. Начиная с конечного события, для которого t_п(n) = t_кр (п – номер конечного события), для каждого события по выходящим из него работам по формуле (6.2) определяем t_п(i) и записываем в правом секторе.

---

4. В нижнем секторе записываем резерв времени события, рассчитанный по формуле (6.3).

5. Критические события имеют резерв времени, равный нулю, они и определяют критические работы и критический путь.

Сетевой график, на котором произведены расчёты, представлен на рисунке 6.3, Числа над дугами соответствуют продолжительности выполнения работ.

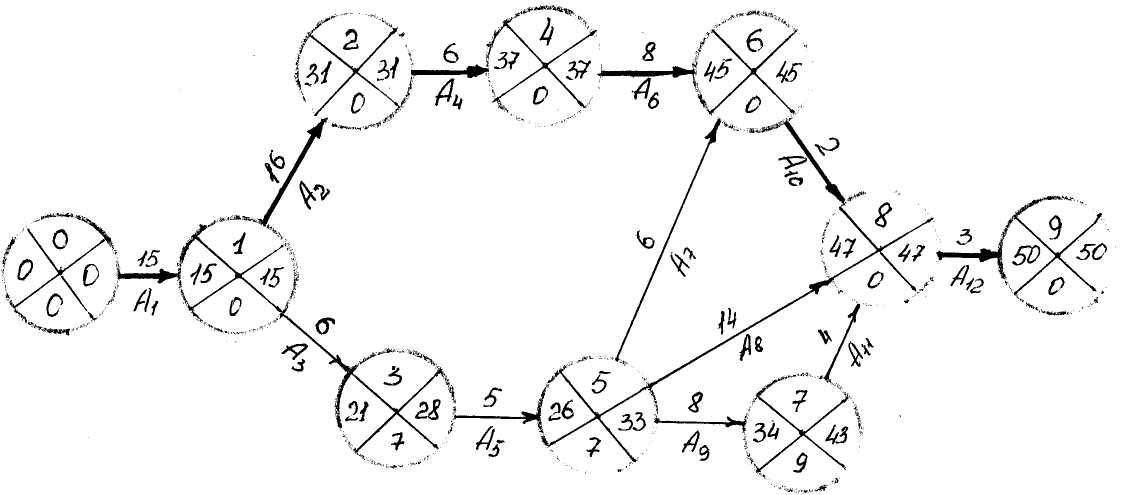
Рисунок 6.3 – Сетевой график с временными параметрами событий
Минимальное время, за которое может быть выполнен весь комплекс работ, равно раннему сроку свершения конечного события сети — 50 дням. События 0, 1, 2, 4, 6, 8, 9 лежат на критическом пути, так как имеют резерв, равный нулю. Работы А₁, А₂, А₄, А₆, А₁₀, А₁₂ принадлежат критическому пути. Сумма продолжительностей этих работ составляет критический срок (15 + 16 + 6 + 8 + 2 + 3 = 50). На рисунке 6.3 критический путь выделен утолщёнными линиями.

Далее рассчитаем ранние и поздние сроки начала и окончания всех работ по формулам:

Ранний срок начала работы (i, j) равен раннему сроку свершения события (i):
t_рн(i,j) = t_p(i). (6.4)
Ранний срок окончания работы равен сумме раннего срока свершения начального события работы и ее продолжительности:
t_ро(i,j) = t_p(i) + t_ijилиt_ро(i,j)= t_рн(i,j) + t_ij. (6.5)
Поздний срок окончания работы совпадает с поздним сро­ком свершения ее конечного события:

t_пo(i,j) = t_п(j). (6.6)
Поздний срок начала работы равен разности между поздним сроком свершения ее конечного события и продолжительностью:
t_пн(i,j) = t_п(j) – t_ij или t_пн(i,j) = t_по(i,j) – t_ij. (6.7)
Полный ре­зерв времени работы – это максимально возможный запас времени, на который можно отсрочить начало работы или уве­личить продолжительность ее выполнения при условии, что конечное для данной работы событие наступит не позднее своего позднего срока. Все некритические работы имеют полный резерв времени отличный от нуля. Полный резерв времени работы рассчитывается по формуле

---

R_п(i,j) = t_п(j) – t_p(i) – t­_ij. (6.8)
Сво­бодный резерв времени – это запас времени, которым можно располагать при выполнении данной работы при условии, что начальное и конечное ее событие наступят в свои ранние сроки. Свободный резерв присущ только данной работе, и его использование никак не повлияет на вы­полнение последующих работ. Только отдельные работы про­екта обладают свободным резервом времени.
R_с(i,j) = t_р(j) – t_р(i) – t_ij. (6.9)
Расчет перечисленных параметров сетевой модели представим в виде таблицы 6.2.

В таблице 6.2 полужирным шрифтом выделены критические работы и их временные параметры.
Таблица 6.2 – Расчет параметров сетевой модели перевода магазина на самообслуживание

Работа (i,j)	Количество предшествующих работ	Продолжительность работ (tij)	Сроки выполнения работ				Резервы времени
			ранние		поздние		работ		событий R(i)
			начала tрн(i,j)	окончания tро(i,j)	начала tпн(i,j)	окончания tпo(i,j)	полный Rп(i,j)	свободный Rс(i,j)
1	2	3	4	5=3+4	6=7-3	7	8=7-5	9=10-8	10
(0,1)	0	15	0	15	0	15	0	0	0
(1,2)	1	16	15	31	15	31	0	0	0
(1,3)	1	6	15	21	22	28	7	0	7
(2,4)	1	6	31	37	31	37	0	0	0
(3,5)	1	5	21	26	28	33	7	0	7
(4,6)	1	8	37	45	37	45	0	0	0
(5,6)	1	6	26	32	39	45	13	13	0
(5,8)	1	14	26	40	33	47	7	7	0
(5,7)	1	8	26	34	35	43	9	0	9
(6,8)	2	2	45	47	45	47	0	0	0
(7,8)	1	4	34	38	43	47	9	9	0
(8,9)	3	3	47	50	47	50	0	0	0

---

Таблица 6.2 заполняется в такой последовательности:

1. 
   графы 1 и 3 заполняются на основе исходных данных, представ­ленных в структурно-временной таблице 6.1;
   
2. 
   графа 2 заполняется в соответствии с количеством предшест­вующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа. Например, в графе 1 имеются три рабо­ты, оканчивающиеся на цифру «8»: (5,8), (6,8), (7,8). Поэтому работе (8,9) предшествуют три работы;
   
3. 
   в графе 4 раннее начало работ, выходящих из исходного события, равно нулю, а раннее окончание этих работ равно их про­должительности (графа 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окон­чания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как будет най­дено раннее окончание предшествующих работ. В свою очередь, раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
   
4. 
   продолжительность критического пути определяется после за­полнения граф 4 и 5 как максимально раннего срока окончания работ, которые ведут к завершающему событию 9;
   
5. 
   найденная величина критического пути Ткр = 50 дней заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, сле­дующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностью. Мини­мальная из величин заносится в графу 7;
   
6. 
   в графе 6 позднее начало работы определяется как разность между поздним окончанием этих работ и их продолжительностью (из значения графы 7 вычитаются данные графы 3);
   
7. 
   в графе 8 полный резерв времени работы определяется как разность между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
   
8. 
   в графе 10 резерв времени событий j определяется как разность между поздним окончанием работы, заканчивающимся событием j графы 7, и ранним началом работы, начинающимся событием j;
   
9. 
   значение свободного резерва времени работы определяется как разность между значениями граф 10 и 8 и указывает на резер­вы, необходимые для оптимизации модели.
   

Пользуясь полученными значениями показателей работ по пере­воду магазина на самообслуживание (таблица 6.2), можно провести анализ сетевой модели, а затем перейти к ее оптимизации.

---

Задачи для самостоятельного решения
Задача 1

Торговая фирма «Астра» запланировала реконструкцию свое­го офиса. Перечень работ, которые необходимо для этого вы­полнить, представлен в таблице 6.3.
Таблица 6.3 – Комплекс работ по реконструкции офиса

Работа	Содержание	Предшествующие работы	Продолжительность, дн.
A1	Определение объема реконструкции	—	5
А2	Составление сметы затрат	A1	10
А3	Выбор проекта реконструкции	A1	5
А4	Выбор строительной организации	А2	3
A5	Получение финансового обеспечения	А2	5
A6	Составление договора на выполнение работ	А4	3
А7	Экономическое обоснование проекта	А3	4
A8	Привязка проекта к условиям фирмы	А7	5
А9	Работа по реконструкции	А5, А6, А8	39

---