Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Рисунок 6.5 – Решение задачи с помощью инструмента Поиск решенияДля нашего примера получаем следующие результаты: ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;

---

; ; ; ;

.
Результаты оптимизации представим на сетевом графике (рисунок 6.6).


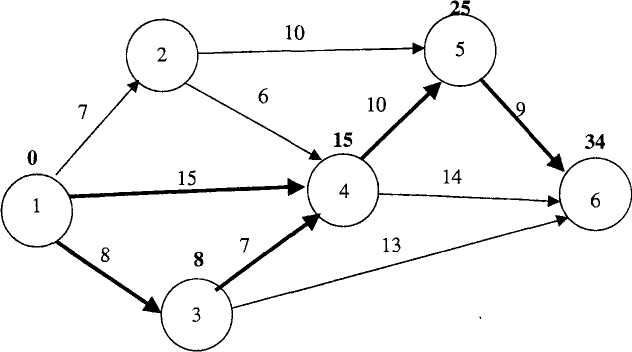
Рисунок 6.6 – Сетевой график в результате оптимизации
4 Анализ полученных результатов.

Чтобы выполнить работы проекта за директивное время t_o= 34, необходимо дополнительно вложить 24 ден. ед. При этом средства распределятся следующим образом: 10 ден. ед. - в работу (1,3), 5 ден. ед. - в работу (1,4), 5 ден. ед. - в работу (3,4) и 4 ден. ед. - в работу (4,5), что приведет к сокращению продолжительности работы (1,3) на 3 дня, работ (1,4) и (3,4) - на 1 день и работы (4,5) - на 2 дня. Сокращение срока реализации проекта за счет вложения дополнительных средств составит 6 ед. времени.
Пример решения задачи 2
Постановка задачи 2. Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность t_ij и минимально возможное время вы­полнения d_ij. Для сокращения срока реализации проекта выделено В ден. ед. Вложение дополнительных средств х_ij в работу (i, j) сокращает время ее выпол­нения до t’_ij = t_ij - k_ijx_ij. Технологические коэффициенты k_ij известны.

Требуется найти такие t^н_ij, t^о_ij, х_ij, чтобы:

- время выполнения всего комплекса работ было минимальным;

- количество используемых дополнительных средств не превышало В ден. ед.;

- продолжительность выполнения каждой работы t_ij была не меньше за­данной величины d_ij.

При выполнении заданий воспользуйтесь данными, приведенными в таблице 6.8.
Таблица 6.8 – Исходные данные для решения задачи

Параметры	Работы							Сумма средств, В
	(1,2)	(1,3)	(1,4)	(2,3)	(3,4)	(3,5)	(4,5)
tij	5	6	2	4	9	7	4	47
dij	3	4	1	2	5	4	2
kij	0,5	0,2	0,3	0,25	0,4	0,2	0,1

---

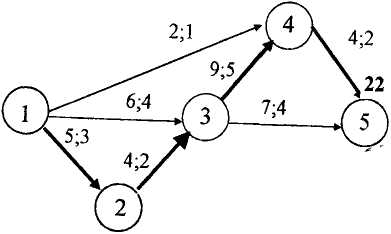
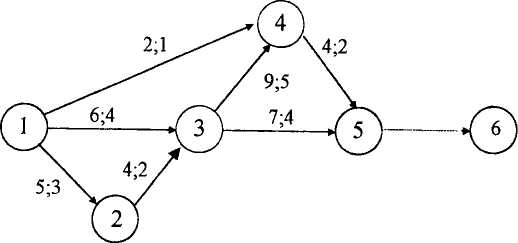
Решение задачи1 Запишем все данные на сетевой график и рассчитаем сроки свершения событий (рисунок 6.7).Рисунок 6.7 – Исходный сетевой графикВидим, что по первоначальному условию t_кр = 22, т.е. проект может быть выполнен за 22 ед. времени.2 Составление математической модели задачи.Чтобы однозначно записать целевую функцию, добавим на сетевом графи­ке (рисунок 6.8) фиктивную работу (5,6).Рисунок 6.8 – Измененный сетевой графикЦелевая функция имеет вид t_кр = t°₅₆ (min). Запишем ограничения задачи:а) сумма вложенных средств не должна превышать их наличного количе­ства:х₁₂ + х₁₃ + х₁₄ + х₂₃ + х₃₄ + х₃₅ + х₄₅< 47;б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени: ; ; ; ; ; ; ; ;в) зависимость продолжительности работ от вложенных средств: ; ; ; ; ; ; ;г) время начала выполнения каждой работы должно быть не меньше вре­мени окончания непосредственно предшествующей ей работы:

---

; ; ; ; ; ; ; ; ; ; ; ;д) условие неотрицательности неизвестных: ; ; ; .3 Технология решения задачи средствами Excel.Сделать форму и ввести данные математической модели на рабочем листе Excel в ячейках А1:АЕ40 (таблица 6.9).Решить данную задачу средствами Excel как оптимизационную с помощью инструмента Поиск решения (рисунок 6.9). 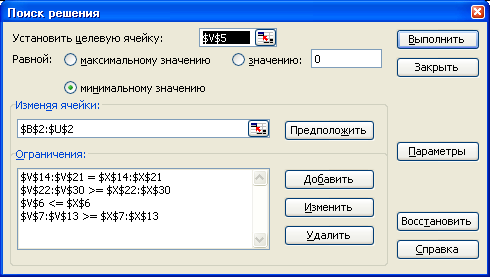В параметрах Поиска решения установить флажки «Линейная модель» и «Неотрицательные значения».Рисунок 6.9 – Решение задачи с помощью инструмента Поиск решенияРешив данную задачу средствами Excel, получаем следующие результа­ты: ; ; ; ; ;

---

;

; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .
Результаты решения представим на сетевом графике (рисунок 6.10).

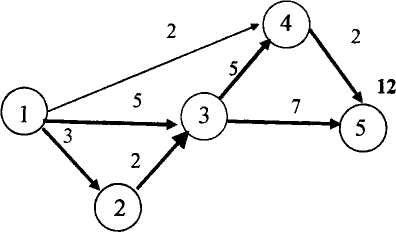
Рисунок 6.10 - Сетевой график в результате оптимизации
4 Анализ полученных результатов.

При дополнительном вложении 47 ден. ед. проект может быть выполнен за 12 ед. времени. При этом средства распре­делятся следующим образом: 4 ден. ед. - в работу (1,2), 5 ден. ед. - в работу (1,3), 8 ден. ед. - в работу (2,3), 10 ден. ед. - в работу (3,4) и 20 ден. ед. - в ра­боту (4,5), что приведет к сокращению продолжительности работ (1,2), (2,3) и (4,5) на 2 дня, работы (1,3) на 1 день, работы (3,4) на 4 дня. Сокращение срока реализации проекта за счет вложения дополнительных средств составит 10 ед. времени.
Задачи для самостоятельного решения

---