Файл: Учебное пособие для студентов специальностей 125 01 10 Коммерческая деятельность.doc

Требуется:1) построить сетевой график проекта;2) рассчитать минимальное время выполнения проекта;3) рассчитать временные параметры свершения событий;4) определить сроки выполнения работ и их резервы времени;5) построить линейный график выполнения работ проекта.Задача 2Торговая фирма готовится принять участие в выс­тавке-ярмарке продовольственных товаров. Перечень работ, которые необходимо выполнить в процессе подготовки, их взаимос­вязь и продолжительность указаны в таблице 6.4.Требуется:1) построить сетевой график проекта;2) выяснить, какое минимальное время необходимо для подготовки к ярмарке;3) выявить резервы работ и «узкие места» всего комплек­са работ;4) построить линейный график (график Ганта) выполне­ния работ.Таблица 6.4 - Перечень работ, их взаимос­вязь и продолжительность

Работа	Содержание работы	Предшест­вующие работы	Продолжи­тельность работы, дн.
A1	—	—	5
А2	Определение размера и типа стенда	А1	1
А3	Определение рекламной стратегии	А1	3
А4	Разработка дизайна проекта экспо­зиции	А1	6
А5	Определение количества и видов рекламно-информационных мате­риалов	А3	2
А6	Оформление заказов; оплата счетов	А5	7
A7	Получение заказов; сортировка, упаковка	А6	12
А8	Заказ оборудования и экспонатов	А4	5
А9	Получение оборудования и экспонатов	A8	14
А10	Техническое и художественное оформление стендов	А9	8
A11	Упаковка и подготовка к транспор­тировке	А10	3
А12	Заключение договора на участие и оплата аренды	A2	4
А13	Бронирование билетов и мест в гостинице	Al2	2
А14	Распределение обязанностей; обучение и инструктаж персонала	А13	6
А15	Переезд и размещение	А14	2
А16	Оформление договоров на дополни­тельные услуги обслуживания на выставке	А12	3
А17	Транспортировка экспозиции и материалов	А7, А11	2
Al8	Установка оборудования и подго­товка стенда к открытию	А15, А16, Al7	2

---

Задача 3Осуществление проекта требует выполнения ряда работ, перечень которых задан в таблице 6.5.

Таблица 6.5 – Перечень работ и их продолжительность

Работа	Непосредственно предшествующая работа	Продолжительность работы, дн.
A1	-	3
А2	-	6
А3	A1	2
А4	А2, А3	5
А5	А4	4
А6	А5	3
А7	А2, А3	9
А8	А6, А7	3

Требуется:1) построить сетевой график проекта;2) рассчитать минимальное время выполнения проекта;3) рассчитать временные параметры свершения событий;4) определить, можно ли отложить выполнение работы А3 без отсрочки завершения проекта в целом;

5) определить, на сколько дней можно отложить выпол­нение работы A6 без отсрочки завершения проекта в целом?

2 Оптимизация сетевого графика по времениРасчет параметров сетевого графика проекта позволяет выявить критические работы, определяющие ход выполнения всего комплекса работ, продолжительность его реализации, ре­зервы времени событий и работ и проанализировать можно ли его использовать в качестве плана выполнения работ. Чаще всего требуется улучшение сетевого графика с учетом сроков выполнения работ и рационального использования материаль­ных, трудовых и денежных ресурсов, т. е. требуется его опти­мизация. Рассмотрим одну из математических моделей оп­тимизационных задач на сетевых графиках, т.е. оптимизацию проекта по времени.

---

Пусть задан срок выполнения проекта t₀, а расчетное t_кр > t₀. В этом случае оптимизация комплекса работ сводится к сокра­щению продолжительности критического пути, которое может быть осуществлено либо за счет перераспределения внутрен­них резервов, либо за счет привлечения дополнительных средств.Сокращение времени завершения проекта, как правило, связано с привлечением дополнительных средств (количес­тво рабочих, сверхурочное время). Рассмотрим два примера постановки задачи оптимизации проекта по времени с при­влечением дополнительных средств.Пример решения задачи 1Постановка задачи 1.Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность t_ij и минимально возможное время вы­полнения d_ij. Пусть задан срок выполнения проекта t_o, а расчетное t_кр > t_о. Про­должительность выполнения работы (i, j) линейно зависит от суммы дополни­тельно вложенных средств х_ij и выражается соотношением: t’_ij = t_ij - k_jjx_ij. Техно­логические коэффициенты k_ij известны.Требуется найти такие t^н_ij, t^о_ij, х_ij, чтобы:- срок выполнения всего комплекса работ не превышал заданной величины t_о;- суммарное количество дополнительно вложенных средств было мини­мальным;- продолжительность выполнения каждой работы t’_ij была не меньше за­данной величины d_ij.При выполнении работы используйте данные, приведенные в таблице 6.6.Таблица 6.6 – Исходные данные по вариантам

Параметры	Работы										Срок выполнения проекта tо
	1,2	1,3	1,4	2,4	2,5	3,4	3,6	4,5	4,6	5,6
tij	7	11	16	6	10	8	13	12	14	9	34
dij	4	8	13	5	7	6	10	10	11	7
kij	0,1	0,3	0,2	0,05	0,25	0,2	0,12	0,5	0,08	0,02

---

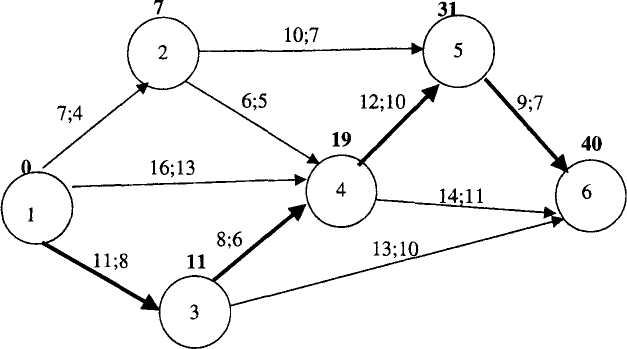
Решение задачи1 Запишем все данные на сетевой график (рисунок 6.4) и рассчитаем сроки свершения событий.Рисунок 6.4 – Исходный сетевой графикРасчеты показали, что срок выполнения проекта t_кр = 40, т.е. превышает директивный срок t_o = 34.2 Составление математической модели задачи Целевая функция имеет видf = х₁₂ + х₁₃ + х₁₄ + х₂₄ + х₂₅ + х₃₄ + х₃₆ + х₄₅ + х₄₆ + х₅₆(min).Запишем ограничения задачи:а) срок выполнения проекта не должен превышать t_о = 34t°₃₆< 34; t°₄₆< 34; t°₅₆< 34;б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени: ; ; ; ; ; ; ; ; ; ;в) зависимость продолжительности работ от вложенных средств: ; ; ; ; ; ;

---

; ; ; ;
г) время начала выполнения каждой работы должно быть не меньше вре­мени окончания непосредственно предшествующей ей работы:

; ; ; ; ;

; ; ; ;

; ; ; ; ;
д) условие неотрицательности неизвестных:

; ; ; .
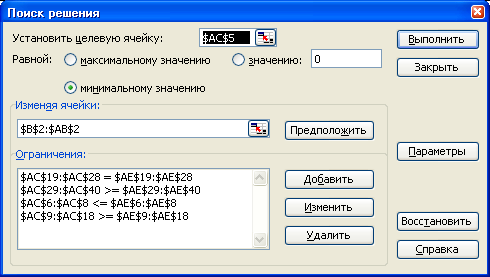
3 Технология решения задачи в Excel.

Сделать форму и ввести данные математической модели на рабочем листе Excel в ячейках А1:АЕ40 (таблица 6.7).

Решить данную задачу средствами Excel как оптимизационную с помощью инструмента Поиск решения (рисунок 6.5). В параметрах Поиска решения установить флажки «Линейная модель» и «Неотрицательные значения».

---