Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 392
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
А определим 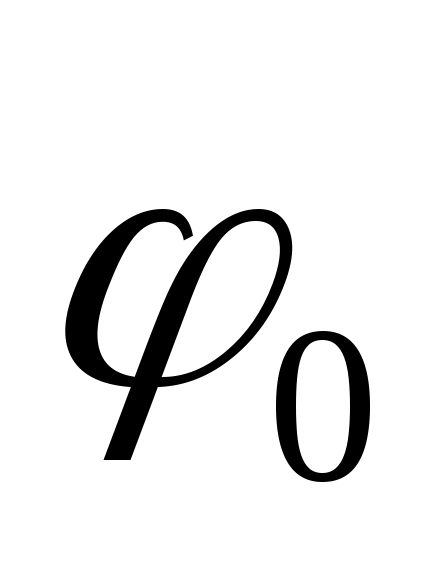 :
:
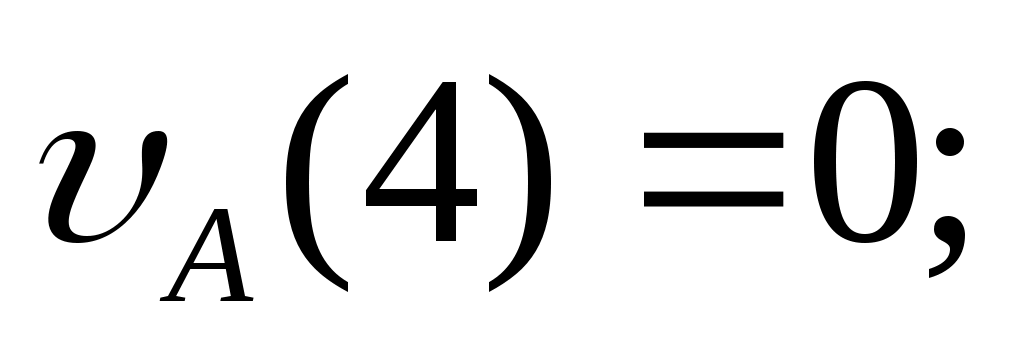
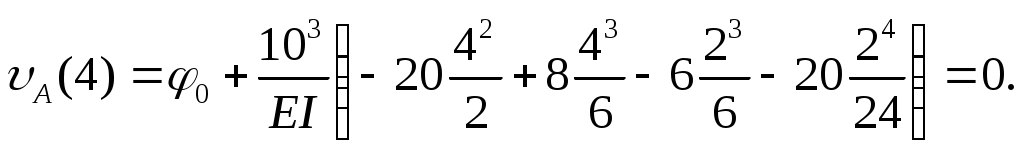
Тогда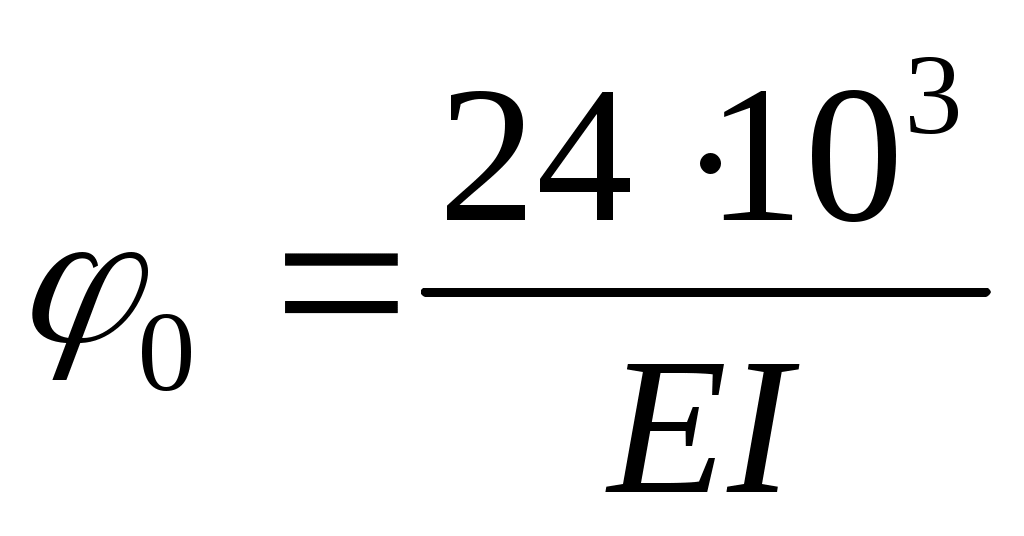 .
.
Окончательно, уравнение прогибов имеет вид
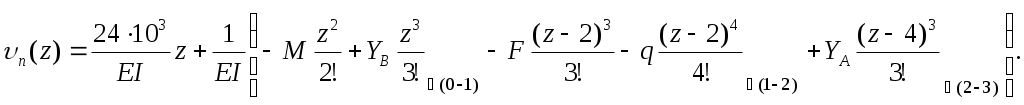
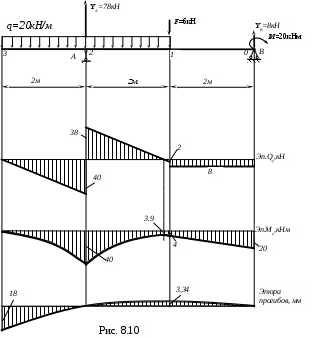
Эпюра прогибов (рис. 8.10) построена для двутавровой балки (№22а, IX=2790cм4).
Вопросы для самопроверки
8.4. Энергетические методы определения перемещений в стержневых
системах
Используя МНП, мы научились определять перемещения в балках с прямой осью. Для брусьев с ломаной или кривой осью применяют метод Мора. Этот метод основан на принципе возможных перемещений (ПВП).
Для удобства введём обозначения:
∆ -перемещение к/л точки по определённому направлению от какой-то силы или группы сил;
- перемещение от силы, равной единице.
Каждое из перемещений обозначается двумя значками, например ΔКF , ΔКt, mnи т.п.
Первый значок обозначает точку, для которой определяется перемещение и направление этого перемещения, а второй значок определяет причину, вызвавшую данное перемещение.
Если перемещение берётся по направлению момента, то оно представляет собой угол поворота.
В курсе теоретической механике для абсолютно жёсткого тела принцип возможных перемещений (ПВП) записывается так:
ΣΑе+ ΣΑi =0, (8.14)
где ΣΑе –сумма работ внешних сил;
ΣΑi - сумма работ внутренних сил.
В курсе сопротивления материалов рассматривается деформируемое упругое тело, поэтому в качестве возможных можно брать конечные малые перемещения, тогда получим
ΣFK Δкn+W кn=0, (8.15)
г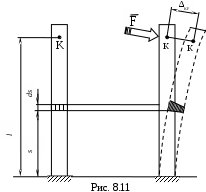 де Δкn –составляющая возможного перемещения точки приложения силы FK, по направлению этой силы от nвозможного перемещения;
де Δкn –составляющая возможного перемещения точки приложения силы FK, по направлению этой силы от nвозможного перемещения;
W кn –работа внутренних сил на n возможном перемещении внутренних частиц.
Предположим, что при возможном перемещении, величина и направлении всех внешних и внутренних сил остаются неизменными, такими же, как в исходном состоянии (перераспределения усилии, связанное с деформацией, не учитывается).
Рассмотрим брус (рис. 8.11), где {F1, F2 ,F3 , Fi,Fn}∞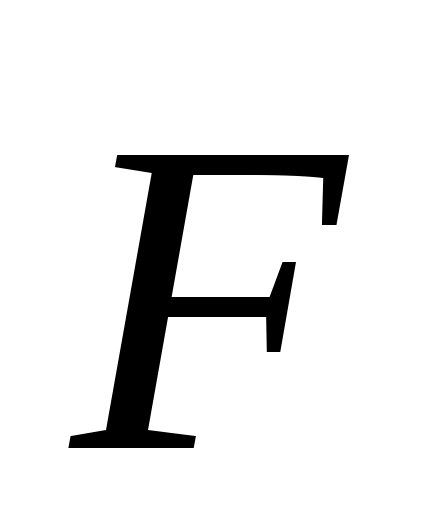 ;
;
ΔКF-перемещение точки К от группы сил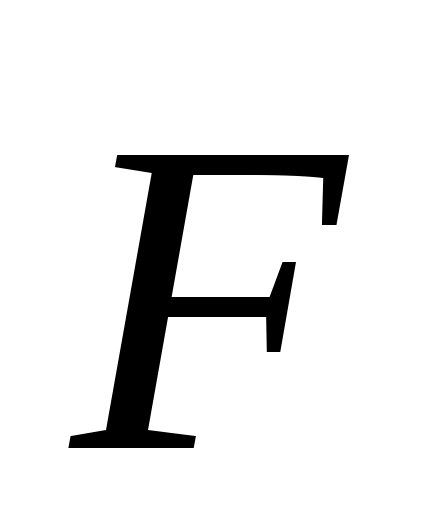 , при деформации стержня на длине l;
, при деформации стержня на длине l;
ds – малый элемент;
dΔКF – перемещение точки К в результате деформации только малого элемента ds
от группы сил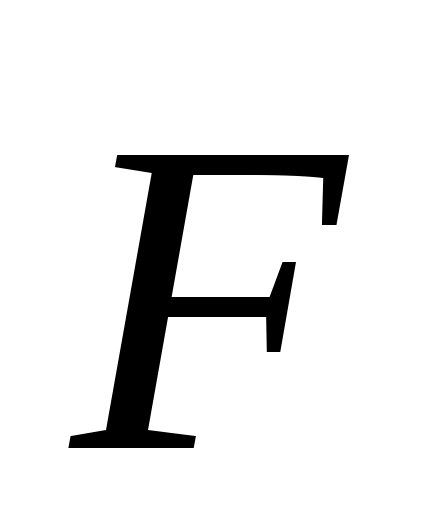 .
.
От группы сил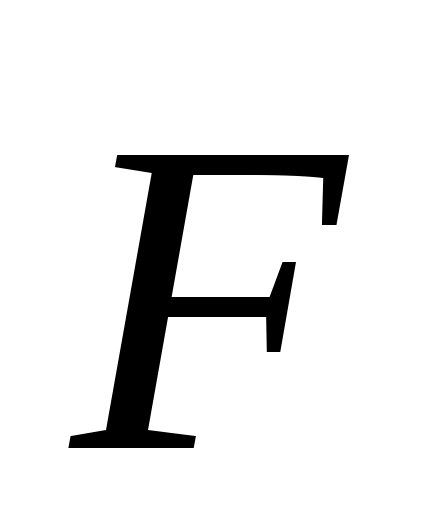 в стержне возникают внутренние усилия: NF, MF, QF= QF(τ), которые в произвольном сечении на длине ds вызывают в плоскости возможные перемещения: Δdz, d, γ (см.рис. 8.12.)
в стержне возникают внутренние усилия: NF, MF, QF= QF(τ), которые в произвольном сечении на длине ds вызывают в плоскости возможные перемещения: Δdz, d, γ (см.рис. 8.12.)
Представим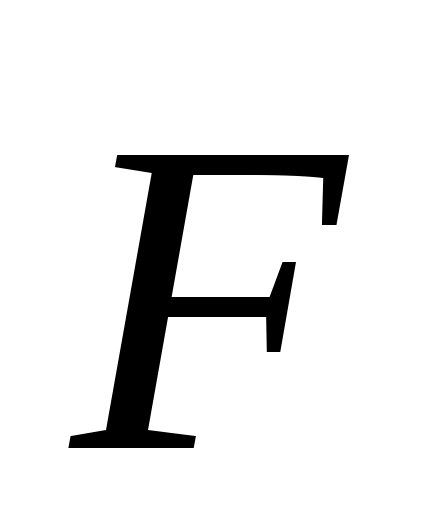 в виде
в виде 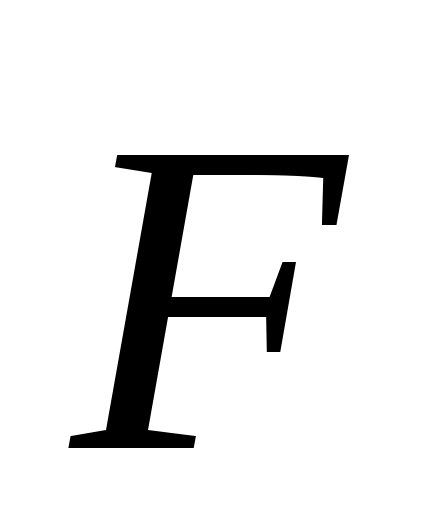 =
=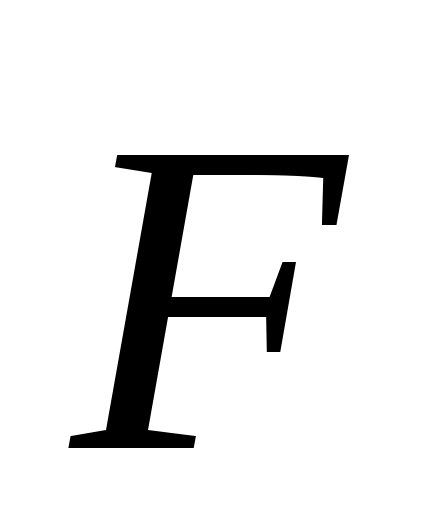 0*F, где
0*F, где 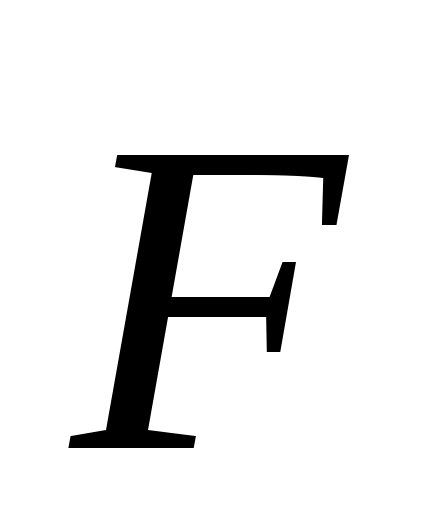
0=1, которая в произвольном сечении должна вызывать внутренние усилия: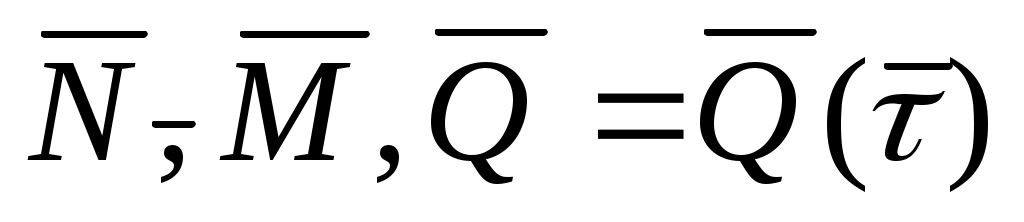 .
.
Если в качестве возможного перемещения, примем перемещения, которые произойдут из-за деформации элемента ds отдействия группы сил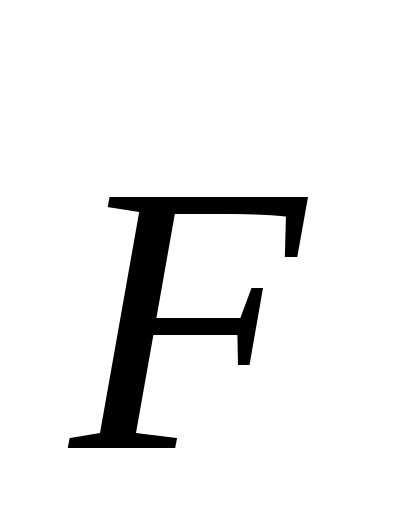 , то составляющие этого возможного перемещения в плоскости будут: Δdz, d и (рис. 8.12.).
, то составляющие этого возможного перемещения в плоскости будут: Δdz, d и (рис. 8.12.).
В этом случае уравнение принципа возможных перемещений от единичной силы запишется так:
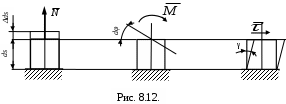
1. dΔКF= .Δds +
.Δds + 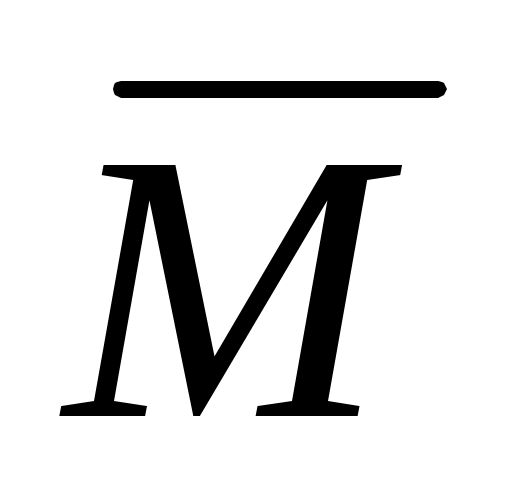 .d +
.d +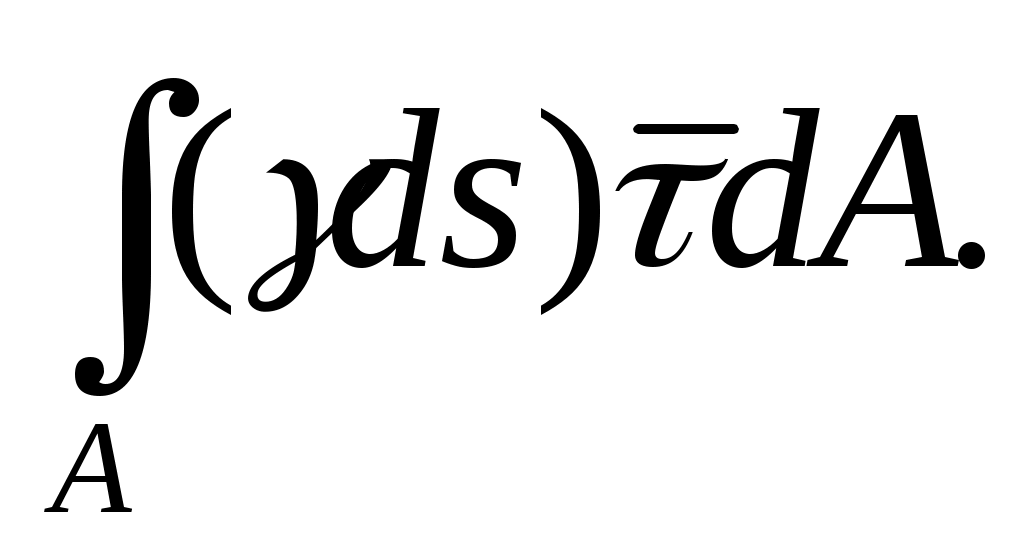 (8.16)
(8.16)
dΔКF= .
.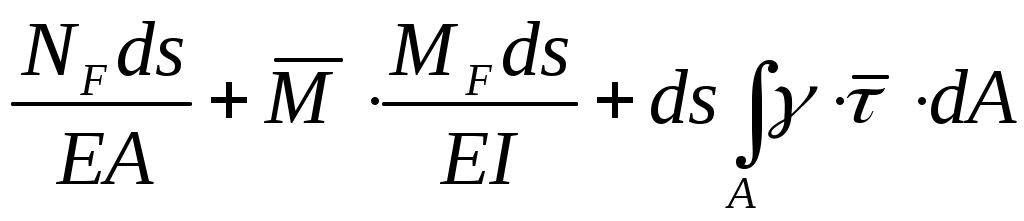 ,
,
где при изгибе: ds=d; d=ds/=MFdz/EJ; J=Ix=I;
при сдвиге: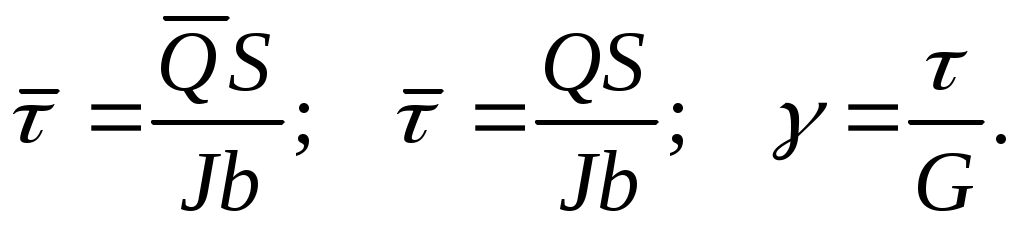
Тогда
dΔКF= .
.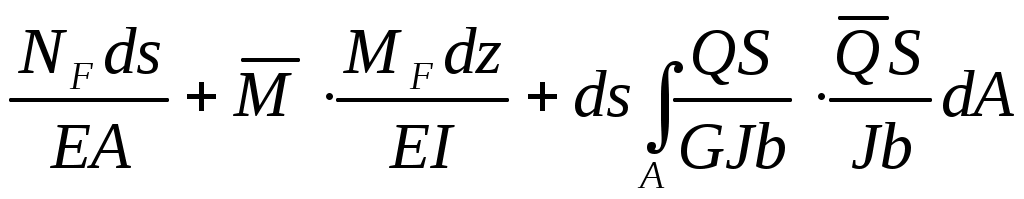 ,
,
выполняя интегрирование, получим формулу Мора
 ΔКF=
ΔКF=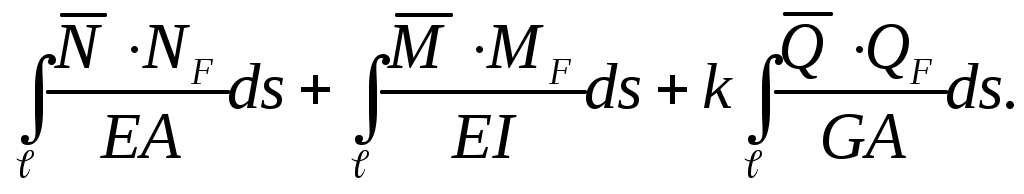 (8.17)
(8.17)
Коэффициент kпредставляет собойбезразмерную величину,
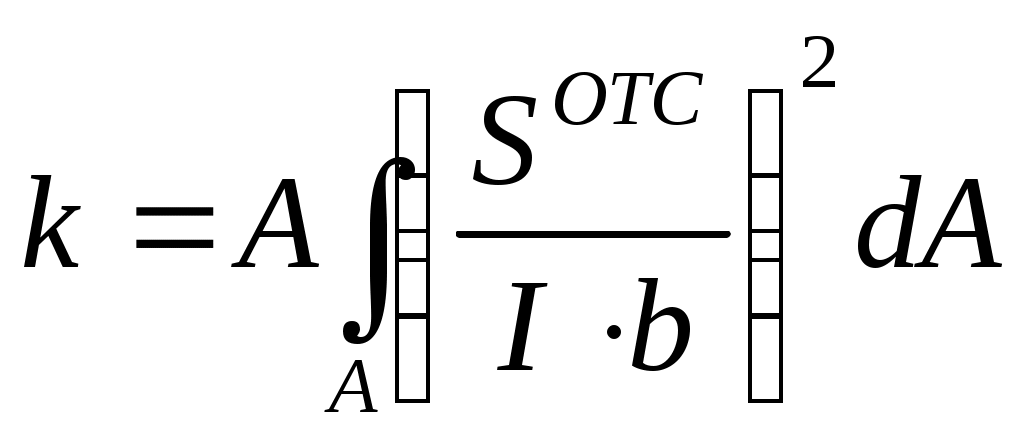
зависящую от геометрической формы сечения, так, например, для прямоугольного сечения k=1,2.
Обычно пренебрегают влиянием нормальных и поперечных сил и тогда формулой Мора учитывают только один интеграл, определяющий изгибные деформации:
ΔКF=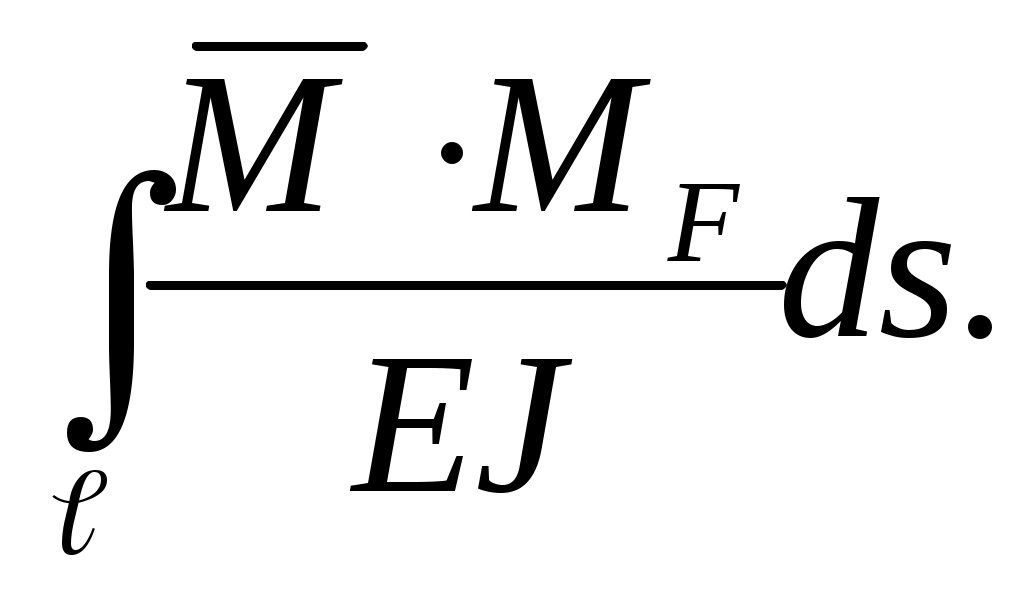
(8.18)
Здесь ΔКF –перемещение (прогиб или угол поворота)
МF –функция моментов от заданной нагрузки;
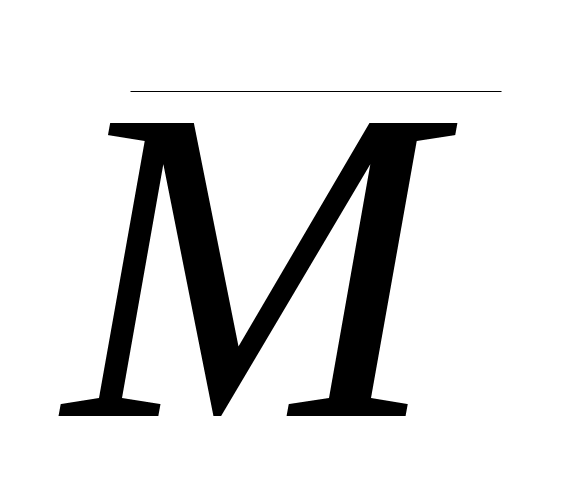 -функция моментов от единичной силы.
-функция моментов от единичной силы.
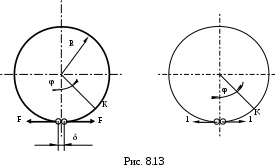
Пример. Определить, на сколько раскроется зазор () в разрезном кольце (см. рис. 8.13) под действием силы F. Жесткость кольца равна EJ.
Для решения используем ΔКF=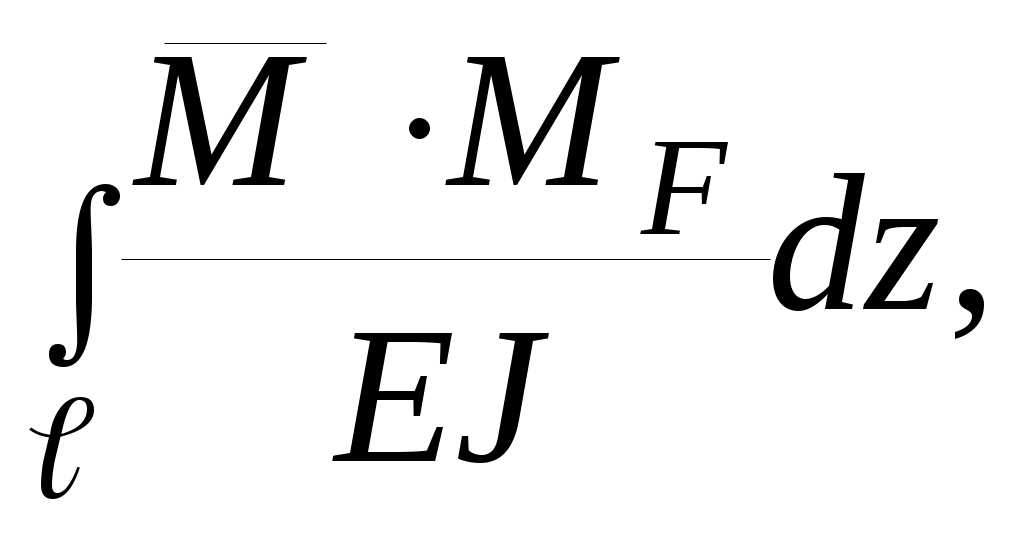 учитывая, что дело имеем с разрезным кольцом, получим:
учитывая, что дело имеем с разрезным кольцом, получим:
=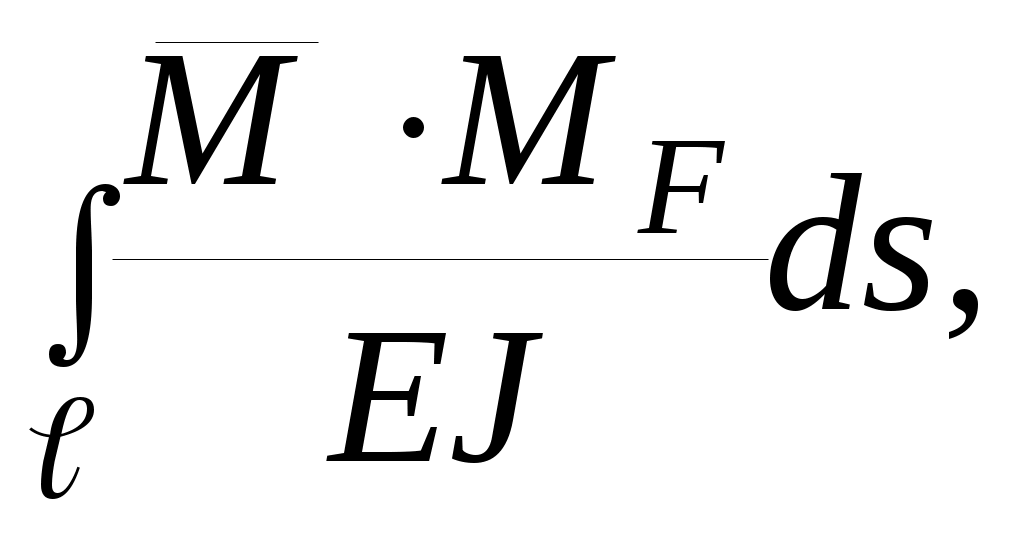
где - l=2R; ds=Rdφ; M=F(R-Rcosφ)=FR(1-cosφ);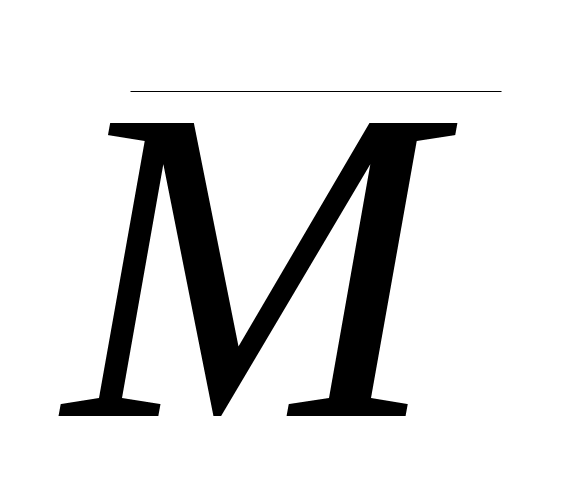 =1(R-Rcosφ)=R(1-cosφ);
=1(R-Rcosφ)=R(1-cosφ);
=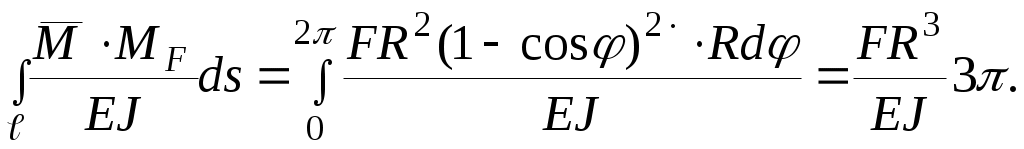
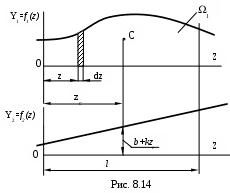
Положим, что на участке длиной l (см. рис. 8.14) нужно взять интеграл от произведения двух функций f1(z)f2(z)
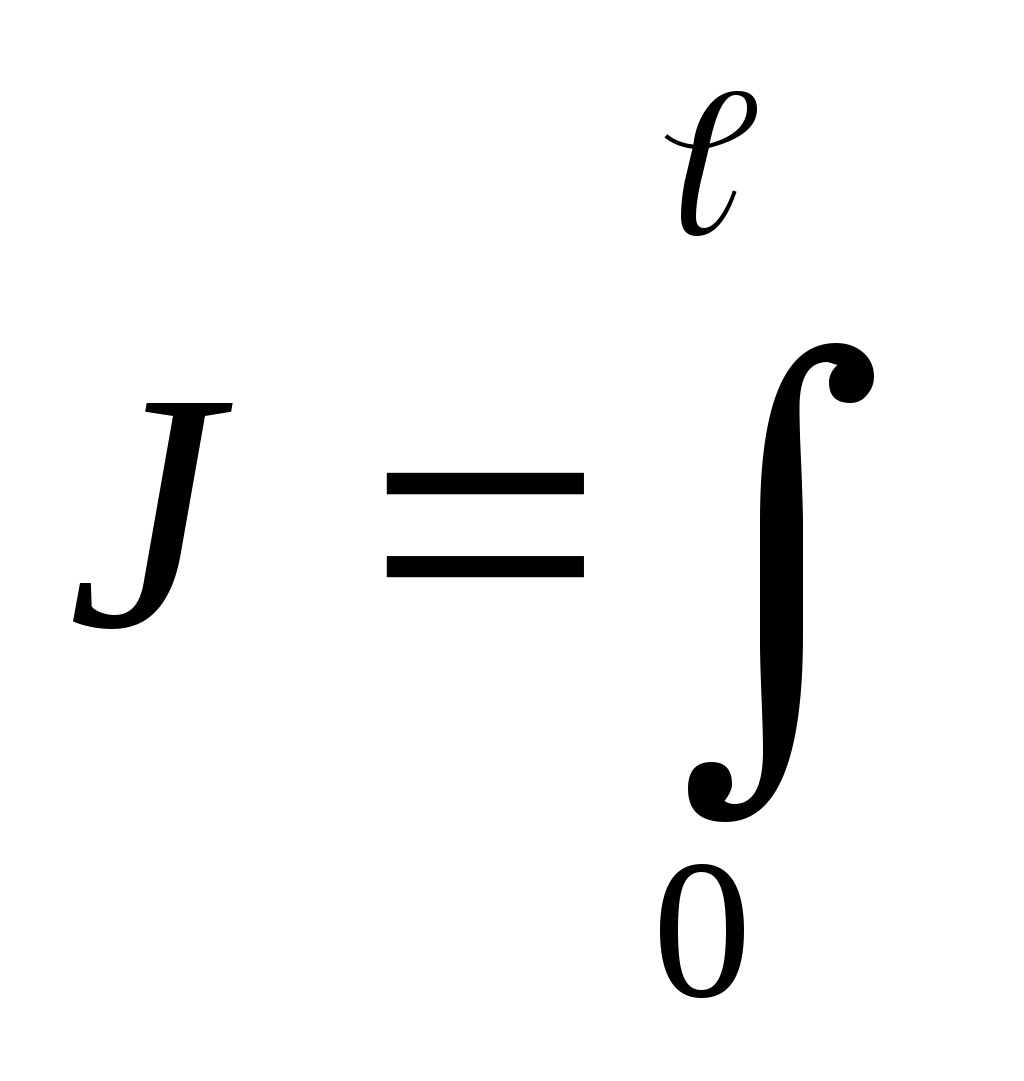 f1(z)f2(z) dz
f1(z)f2(z) dz (8.19)
(8.19)
при условии, что функция f2(z) – линейная. Пусть f2(z)=b+kz.
Тогда выражение (8.19) примет вид
J=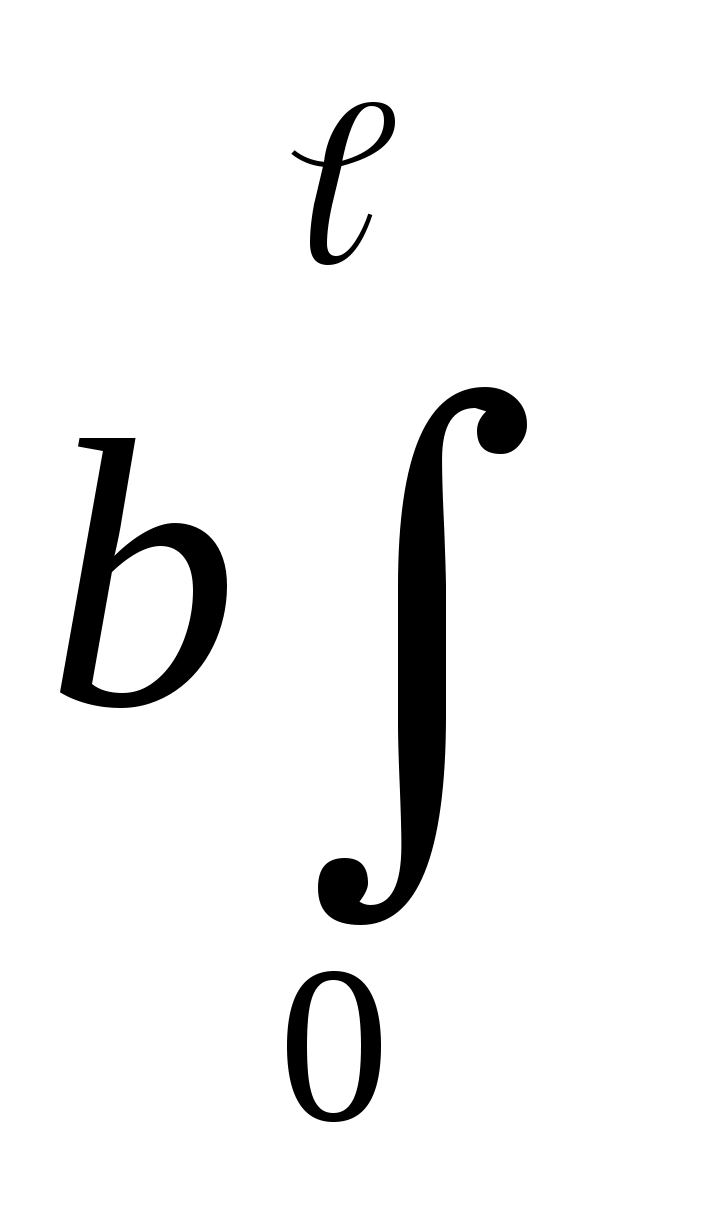 f1(z)dz+
f1(z)dz+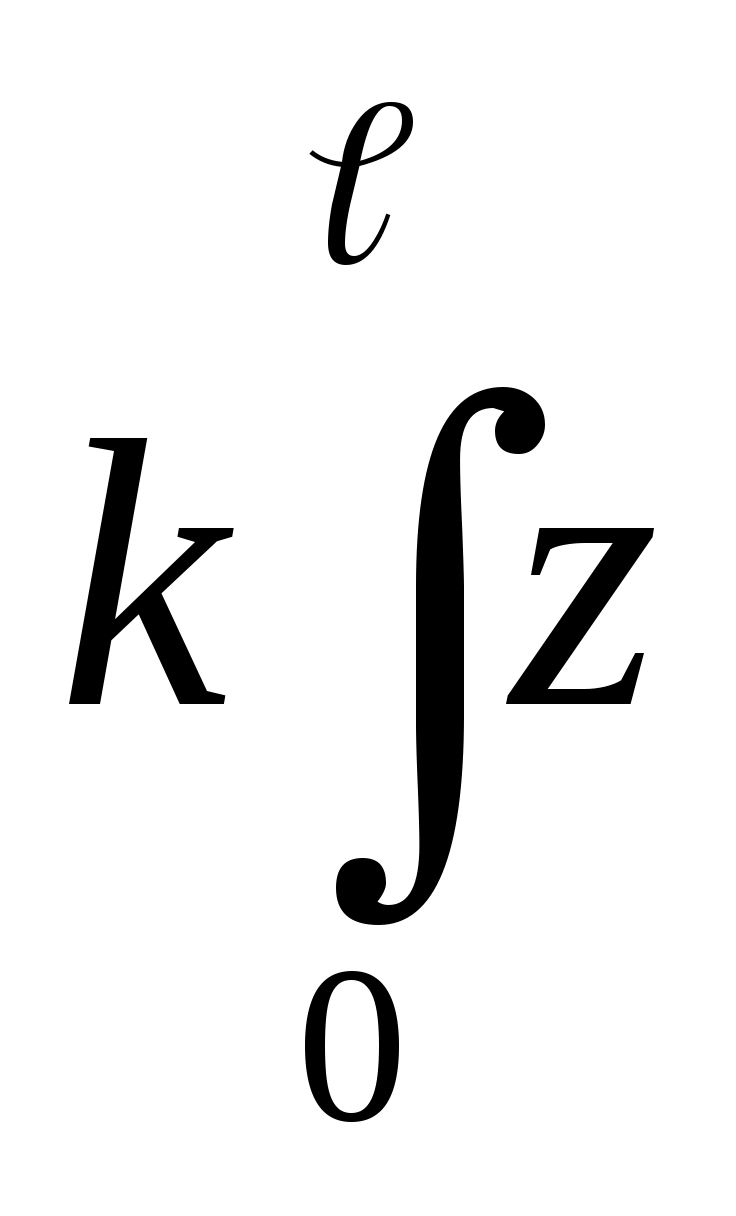 f1(z)dz.
f1(z)dz.
Первый из интегралов представляет собой площадь 1, ограниченную
кривой f1(z) ( см.рис.).
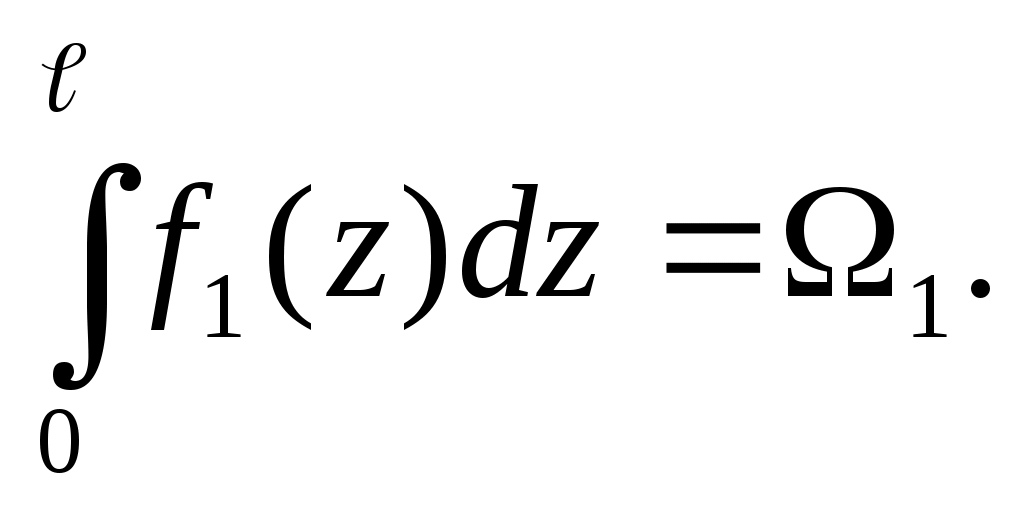
Второй интеграл представляет собой статический момент этой площади относительно оси Y1, т.е.
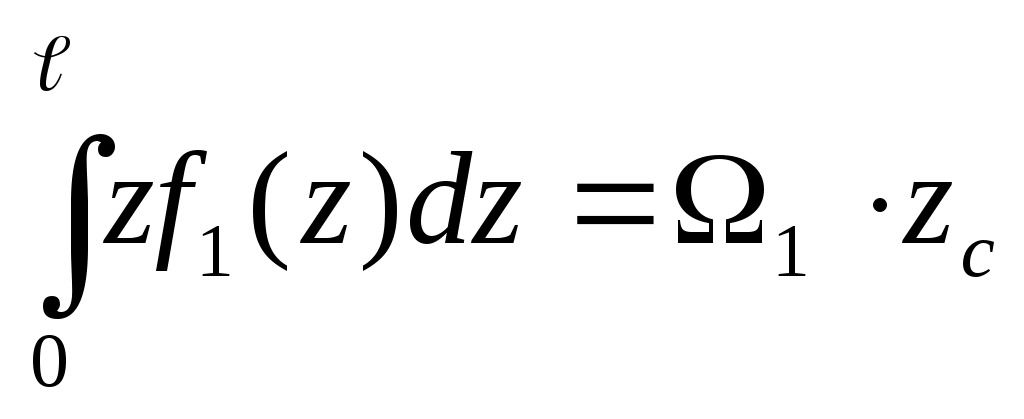
,
где zc – координата центра тяжести (1) – первой эпюры. Получаем
J=1(b+kzc).
Но
(b+kzc)=f2(zc).
Следовательно,
J=1 f2(zc).(8.20)
Таким образом, по способу Верещагина операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой. Эпюры от единичных силовых факторов на прямолинейных участках всегда линейные.
Если обе функции линейные, операция перемножения обладает свойством коммутативности.
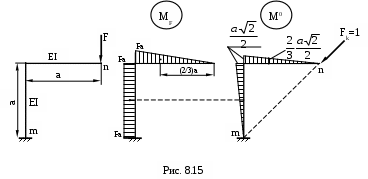
Пример. Определить, на сколько изменится расстояние между точками m и n (см. рис. 8.15) в результате деформации от изгиба рамы под действием силы F. Жесткости обоих стержней одинаковые и равны EI. Построим эпюру изгибающих моментов (МF) от заданной нагрузки на растянутых волокнах. Эпюру (М0) строим от силы Fк=1, приложенной в точке n по направлению к точке m, также на растянутых волокнах.
Пользуясь способом Верещагина, находим
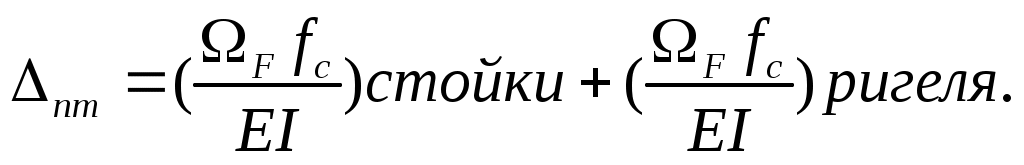
Вычисления дают
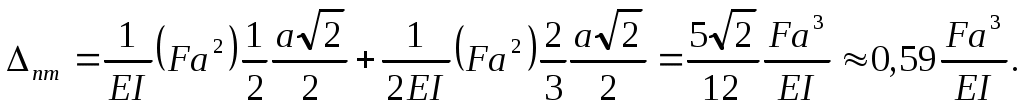
8.5. Теорема о взаимности работ
Представим потенциальную энергию при изгибе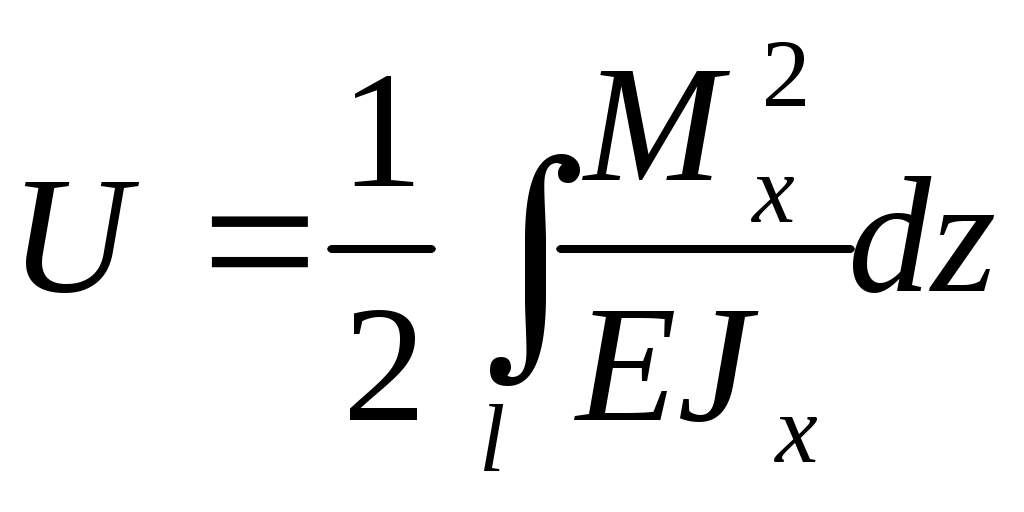 , учитывая, что
, учитывая, что 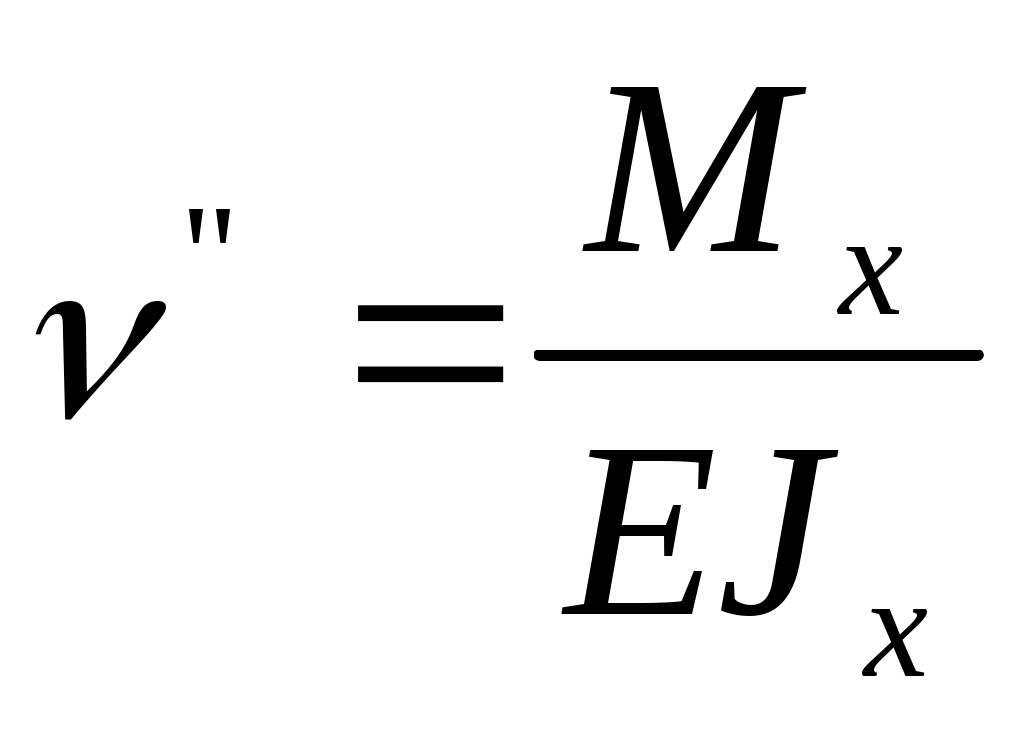 , тогда
, тогда 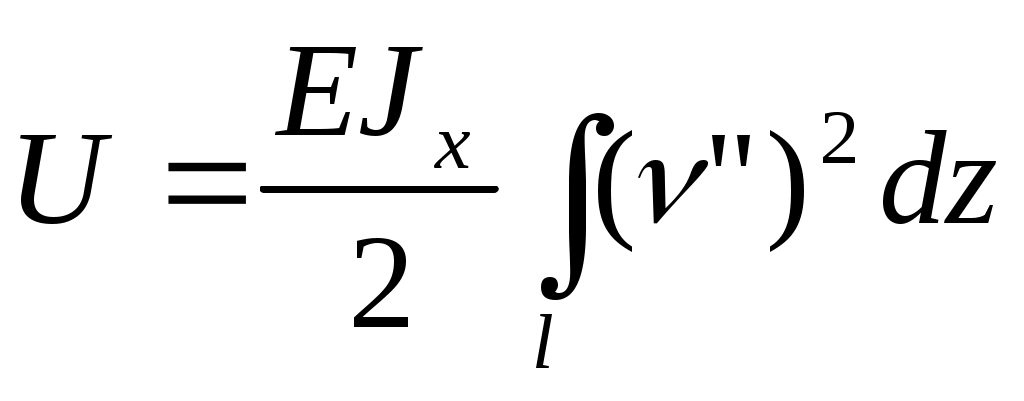 , откуда следует, что потенциальная
, откуда следует, что потенциальная энергия в стержне при изгибе зависит только от характера (формы, вида) изгиба и не зависит от истории (порядка) нагружения.
энергия в стержне при изгибе зависит только от характера (формы, вида) изгиба и не зависит от истории (порядка) нагружения.
Воспользуемся этим и дважды загрузим балку силами F1 и F2.
1ый -случай
1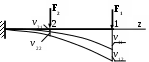 . Статически нагружаем балку силой F
. Статически нагружаем балку силой F
Тогда
Окончательно, уравнение прогибов имеет вид
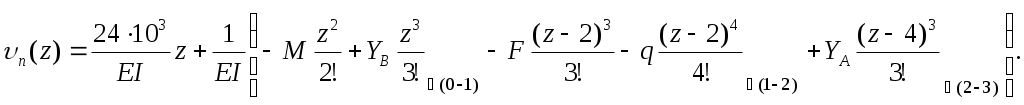
Эпюра прогибов (рис. 8.10) построена для двутавровой балки (№22а, IX=2790cм4).

Вопросы для самопроверки
-
Почему основное дифференциальное уравнением изогнутой оси является приближенным? -
Какими основными величинами характеризуется деформация балки? -
С помощью, каких условий находятся произвольные постоянные интегрирования дифференциального уравнения изогнутой оси? -
Почему интегрирование дифференциальных уравнений должно проводиться без раскрытия скобок? -
В чем геометрическая сущность условий на границе между двумя участками балки? -
В чем сущность метода начальных параметров? -
Как определить наибольшую величину прогиба?
8.4. Энергетические методы определения перемещений в стержневых
системах
-
8.4.1. Метод Мора для определения перемещений -
Используя МНП, мы научились определять перемещения в балках с прямой осью. Для брусьев с ломаной или кривой осью применяют метод Мора. Этот метод основан на принципе возможных перемещений (ПВП).
Для удобства введём обозначения:
∆ -перемещение к/л точки по определённому направлению от какой-то силы или группы сил;
- перемещение от силы, равной единице.
Каждое из перемещений обозначается двумя значками, например ΔКF , ΔКt, mnи т.п.
Первый значок обозначает точку, для которой определяется перемещение и направление этого перемещения, а второй значок определяет причину, вызвавшую данное перемещение.
Если перемещение берётся по направлению момента, то оно представляет собой угол поворота.
В курсе теоретической механике для абсолютно жёсткого тела принцип возможных перемещений (ПВП) записывается так:
ΣΑе+ ΣΑi =0, (8.14)
где ΣΑе –сумма работ внешних сил;
ΣΑi - сумма работ внутренних сил.
В курсе сопротивления материалов рассматривается деформируемое упругое тело, поэтому в качестве возможных можно брать конечные малые перемещения, тогда получим
ΣFK Δкn+W кn=0, (8.15)
г
 де Δкn –составляющая возможного перемещения точки приложения силы FK, по направлению этой силы от nвозможного перемещения;
де Δкn –составляющая возможного перемещения точки приложения силы FK, по направлению этой силы от nвозможного перемещения;W кn –работа внутренних сил на n возможном перемещении внутренних частиц.
Предположим, что при возможном перемещении, величина и направлении всех внешних и внутренних сил остаются неизменными, такими же, как в исходном состоянии (перераспределения усилии, связанное с деформацией, не учитывается).
Рассмотрим брус (рис. 8.11), где {F1, F2 ,F3 , Fi,Fn}∞
ΔКF-перемещение точки К от группы сил
ds – малый элемент;
dΔКF – перемещение точки К в результате деформации только малого элемента ds
от группы сил
От группы сил
Представим
0=1, которая в произвольном сечении должна вызывать внутренние усилия:
Если в качестве возможного перемещения, примем перемещения, которые произойдут из-за деформации элемента ds отдействия группы сил
В этом случае уравнение принципа возможных перемещений от единичной силы запишется так:

1. dΔКF=
dΔКF=
где при изгибе: ds=d; d=ds/=MFdz/EJ; J=Ix=I;
при сдвиге:
Тогда
dΔКF=
выполняя интегрирование, получим формулу Мора
Коэффициент kпредставляет собойбезразмерную величину,
зависящую от геометрической формы сечения, так, например, для прямоугольного сечения k=1,2.
Обычно пренебрегают влиянием нормальных и поперечных сил и тогда формулой Мора учитывают только один интеграл, определяющий изгибные деформации:
ΔКF=
(8.18)
Здесь ΔКF –перемещение (прогиб или угол поворота)
МF –функция моментов от заданной нагрузки;

Пример. Определить, на сколько раскроется зазор () в разрезном кольце (см. рис. 8.13) под действием силы F. Жесткость кольца равна EJ.
Для решения используем ΔКF=
=
где - l=2R; ds=Rdφ; M=F(R-Rcosφ)=FR(1-cosφ);
=
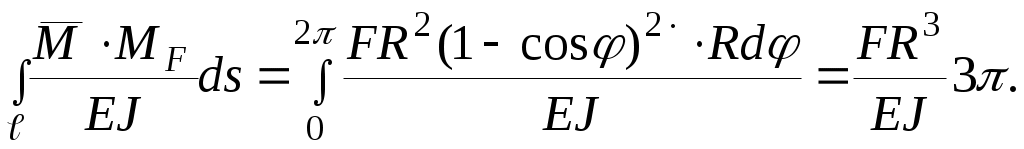
-
8.4.2. Способ Верещагина для определения перемещений
Положим, что на участке длиной l (см. рис. 8.14) нужно взять интеграл от произведения двух функций f1(z)f2(z)
при условии, что функция f2(z) – линейная. Пусть f2(z)=b+kz.
Тогда выражение (8.19) примет вид
J=
Первый из интегралов представляет собой площадь 1, ограниченную
кривой f1(z) ( см.рис.).
Второй интеграл представляет собой статический момент этой площади относительно оси Y1, т.е.
,
где zc – координата центра тяжести (1) – первой эпюры. Получаем
J=1(b+kzc).
Но
(b+kzc)=f2(zc).
Следовательно,
J=1 f2(zc).(8.20)
Таким образом, по способу Верещагина операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой. Эпюры от единичных силовых факторов на прямолинейных участках всегда линейные.
Если обе функции линейные, операция перемножения обладает свойством коммутативности.

Пример. Определить, на сколько изменится расстояние между точками m и n (см. рис. 8.15) в результате деформации от изгиба рамы под действием силы F. Жесткости обоих стержней одинаковые и равны EI. Построим эпюру изгибающих моментов (МF) от заданной нагрузки на растянутых волокнах. Эпюру (М0) строим от силы Fк=1, приложенной в точке n по направлению к точке m, также на растянутых волокнах.
Пользуясь способом Верещагина, находим
Вычисления дают

8.5. Теорема о взаимности работ
Представим потенциальную энергию при изгибе
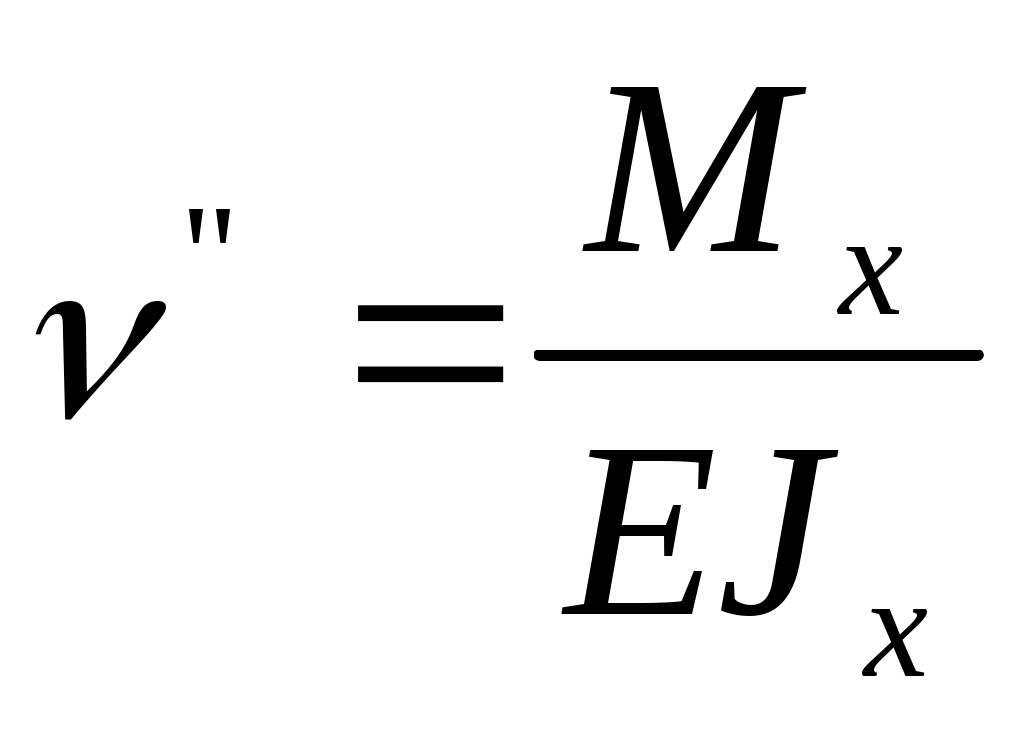 , тогда
, тогда 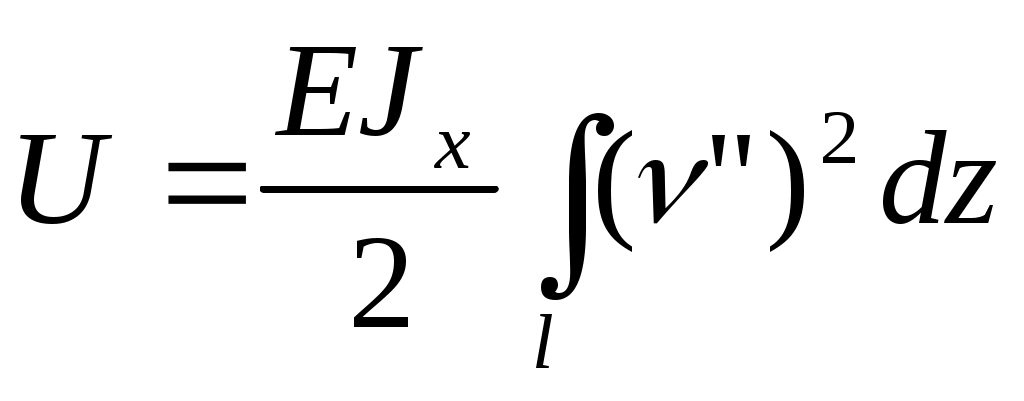 , откуда следует, что потенциальная
, откуда следует, что потенциальнаяВоспользуемся этим и дважды загрузим балку силами F1 и F2.
1ый -случай
1
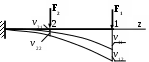 . Статически нагружаем балку силой F
. Статически нагружаем балку силой F