Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 409
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
1
в точке 1;
2. Затем силой F2 в точке 2.
Учтем, что мерой энергии является работа.
Тогда:

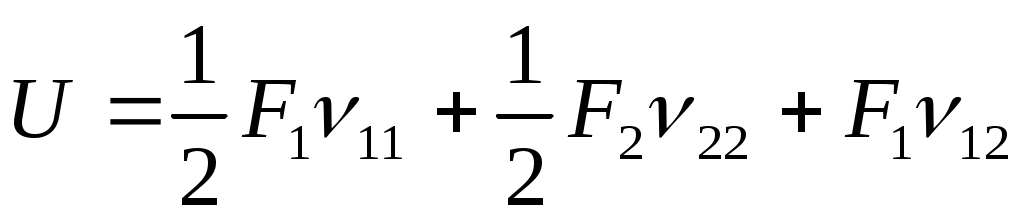 (8.21)
(8.21)
IIой –случай Статически загрузим балку сначала силой F2, а затем силой F1, получаем
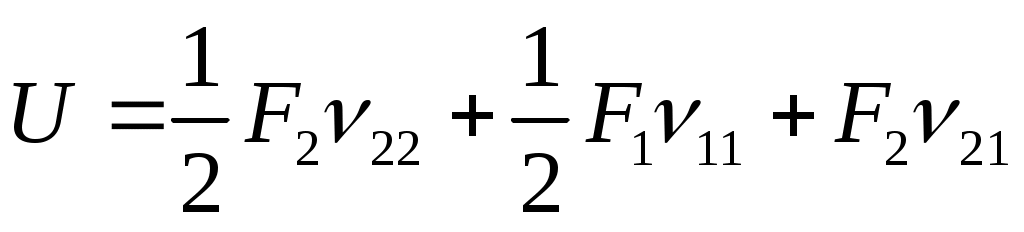 . (8.22)
. (8.22)
Сравним оба значения U, получим
теорему о взаимности работ
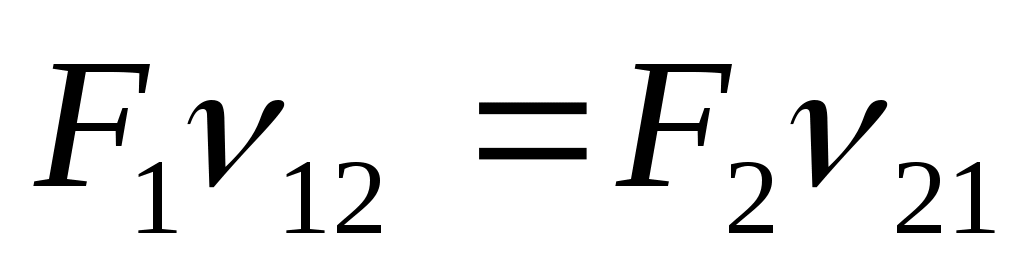 (8.23)
(8.23)
Работа силы F1 на перемещениях, вызванных силой F2 , равна работе силы F2 на перемещениях, вызванных силой F1.
Частный случай при F1 = F2 , получим теорему о взаимности перемещений
v12= v21(8.24)
точки 2, вызнанный такой же силой, но приложенной в точке 1.
P.S.-теорему широко использует служба госгортехнадзора.
Вопросы для самопроверки
6. Почему теорему о взаимности перемещений широко использует служба Госгортехнадзора?
9. Простейшие статически неопределимые стержневые системы и балки
9.1. Статически неопределимые стержневые конструкции
Стержневая конструкция называется статически определимой, если в ней, при любом загружении, усилия во всех элементах могут быть определимы из одних уравнений статики.
Статически неопределимыми конструкциями (СНК) называются такие конструкции, в элементах которых усилия не могут быть определены при помощи только одних уравнений статики.
Кроме уравнений статики, для расчета статически неопределимых конструкций необходимо использовать уравнения, содержащие деформации элементов конструкции.
Все статически неопределимые конструкции имеют так называемые
«лишние» связи в виде закреплений, опор, т.к. при их отсутствии прочность и жесткость конструкции может оказаться необеспеченной. Лишними такие связи называются потому, что они не являются необходимыми для объяснения равновесия остальных элементов конструкции и её геометрической (кинематической) неизменяемости.
По условию прочности или жесткости конструкции «лишние» связи могут оказаться необходимыми.
Статически неопределимые конструкции, элементы которых работают на растяжение и сжатие, мы будем рассчитывать путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической стороны задачи.
При этом будем придерживаться следующего порядка.
9.1.1. Статически неопределимые стержневые конструкции, работающие на растяжение и сжатие
9.1.1.1. Раскрытие статической неопределимости при помощи
уравнений совместности деформаций. Зависимости усилий от отношения жесткостей
Пример 1. Определим напряжение в призматическом стержне (EA=const), заделанном двумя концами, от силы F (рис. 9.1, а)
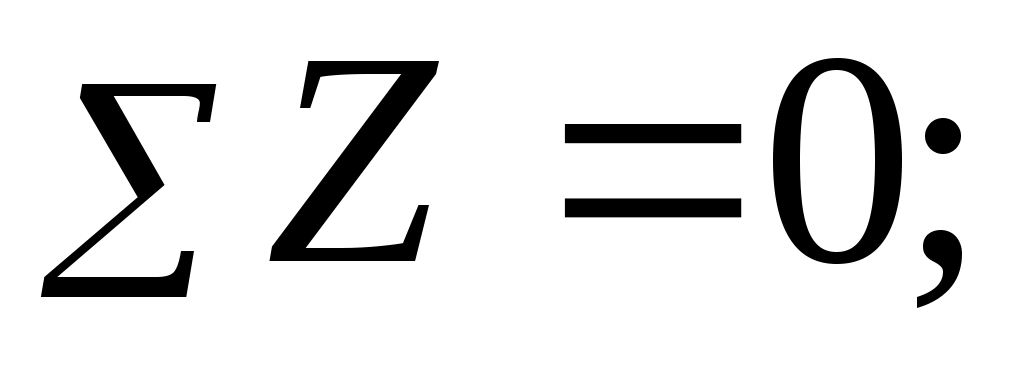
-D+F-B=0, (9.1)
D = F– B.
Две неизвестных реакции и одно уравнение статики, следовательно, задача один раз статически неопределима.

Так как концы стержня жестко закреплены, то длина его не изменяется:
l=0 . (9.2)
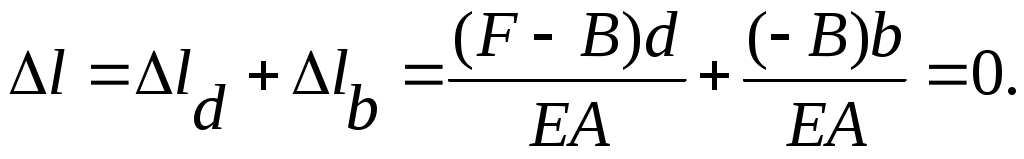 (9.3)
(9.3)
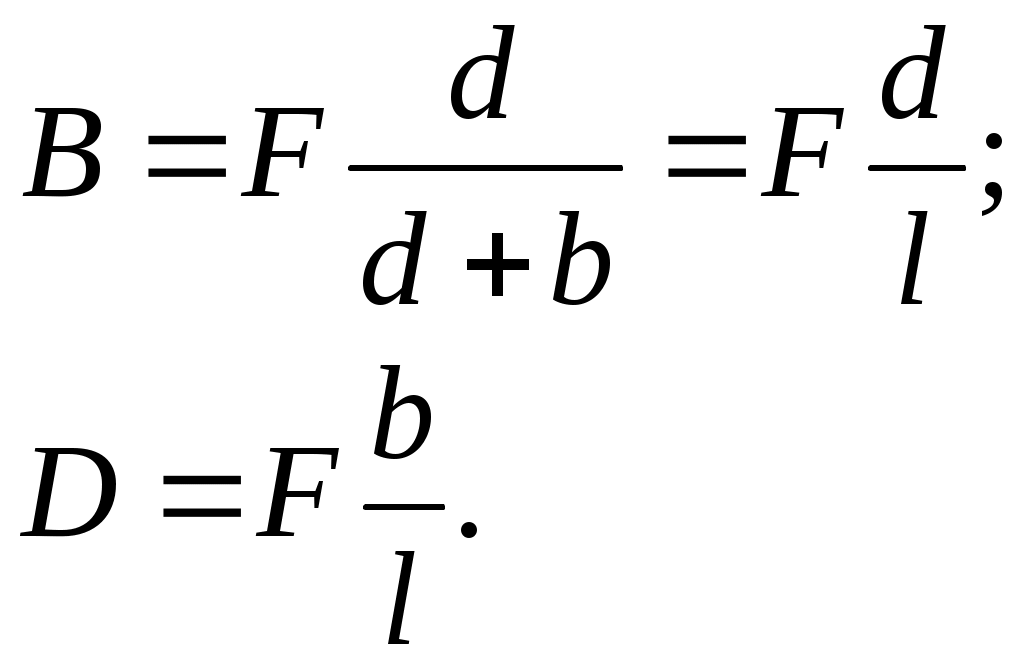
Строим эпюру внутренних сил (см. рис. 9.1, в).
Наибольшие напряжения равны
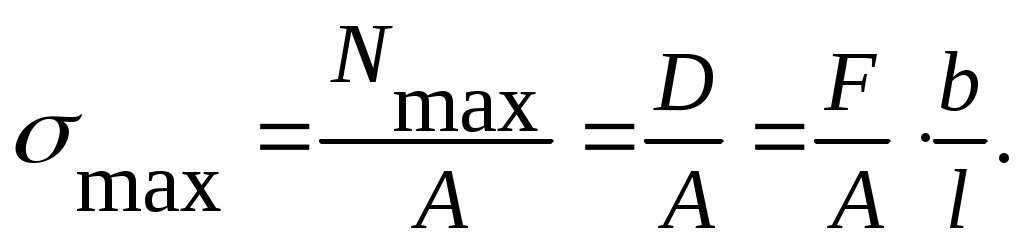
Для простоты рассуждения зададимся: d=l/3, b=2l/3. Тогда
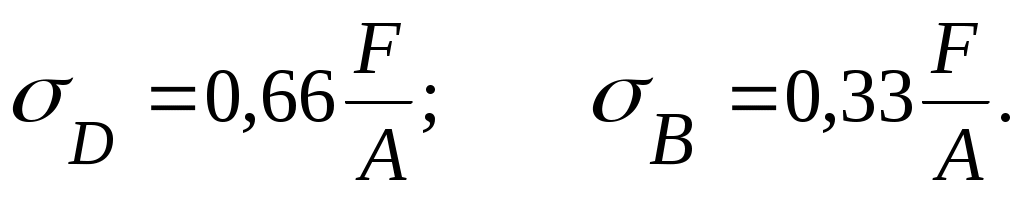
Казалось бы, необходимо увеличить левое сечение в 2 раза.
Сделаем это: рассмотрим уравнение (9.3)
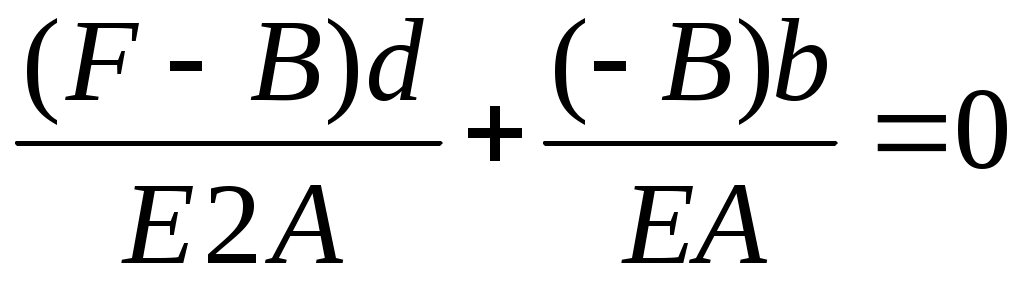 .
.
Получаем D=0.8F; B=0.2F.
D=0.4(F/A); B=0.2(F/A).
Видно, что увеличение площади одного из участков, ведет к перераспределению напряжения во всех элементах системы.
П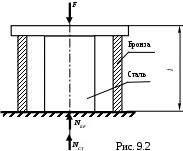
ример 2. Определить внутренние усилия в стальном стержне и бронзовой трубке, которые загружены усилием F через абсолютно твердую плиту, уложенную на них без зазора.
1. Z=0; NБР + NСТ - F=0.
2. lБР = lСТ.
3.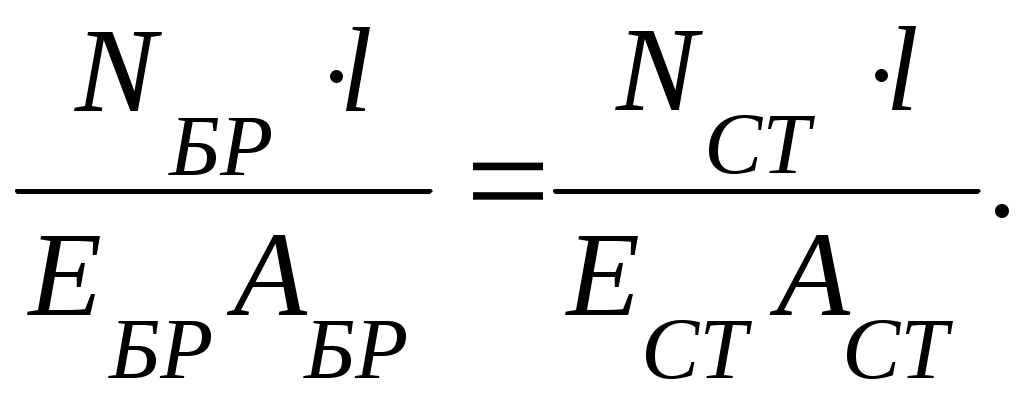
4.

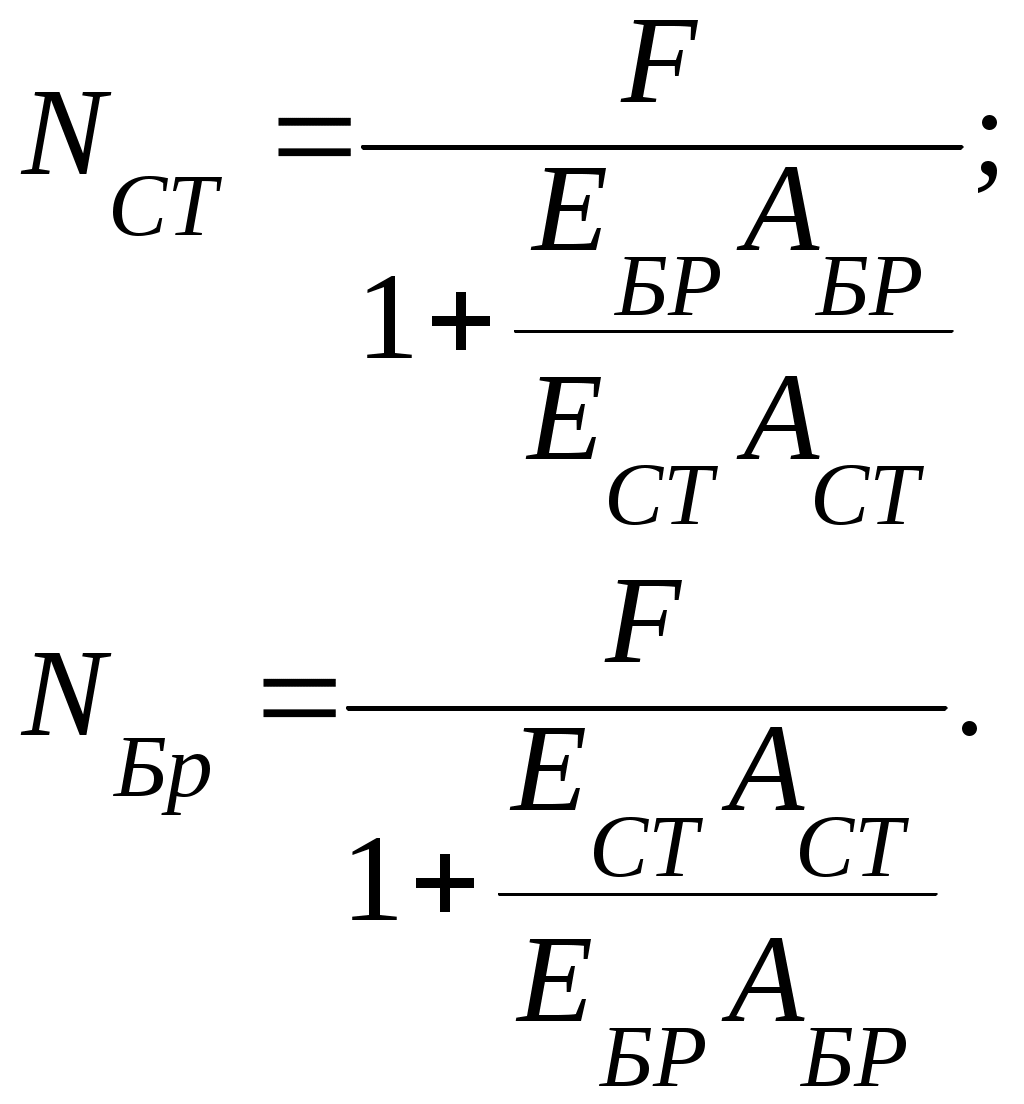
Распределение усилия зависит от отношения жесткостей отдельных элементов.
П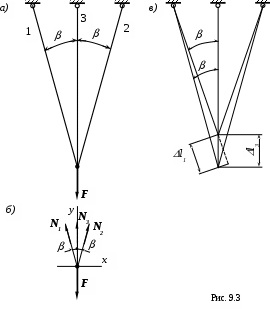
ример 3. Определить внутренние усилия в стержневой системе.
1. X=0; -N1sin + N2sin =0;
Y=0; N1cos +N3+ N2cos -F=0. (9.4)
Из первого уравнения N1= N2 ,
тогда из второго 2N1cos + N3 - F=0,
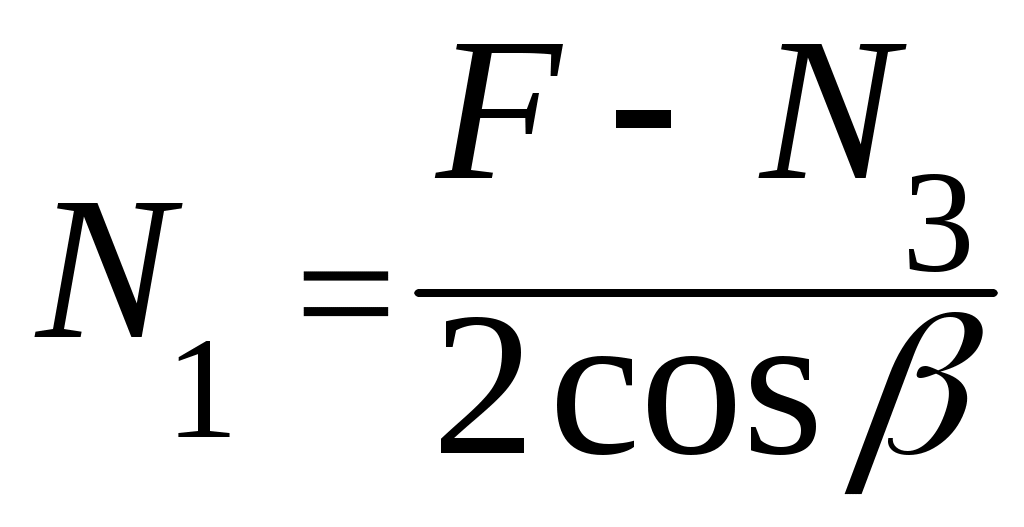 . (9.5)
. (9.5)
2. Под действием силы Fвсетри стержня растягиваются, во всех трех возникают деформации растяжения.
Растягивающие усилия в стержнях должны быть такими, чтобы соблюдалось согласование в деформациях (согласование в удлинениях). Согласование состоит в том, что после деформации, как и до неё, нижние концы всех трех стержней должны быть в одной точке.
Учитывая, что деформации малы, будем считать, что углы не изменяются. Тогда
l1 =l3cos . (9.6)
Уравнение (9.6) рассматривают как уравнение совместности деформации.
3.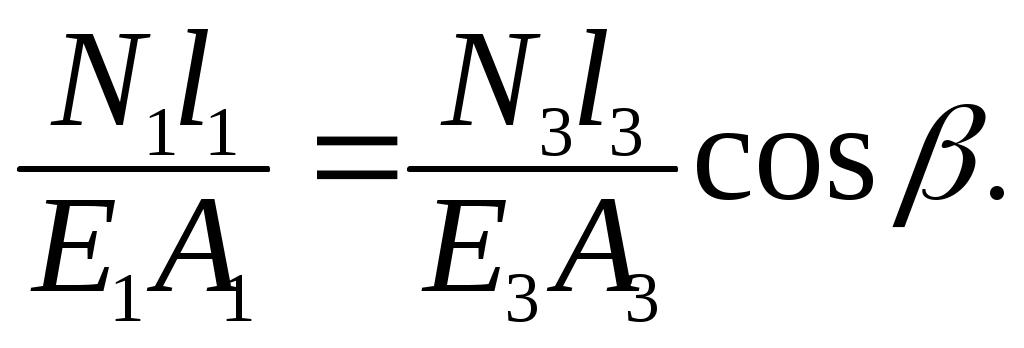 (9.7)
(9.7)
4. Учтем , что l3 =l1cos, отсюда
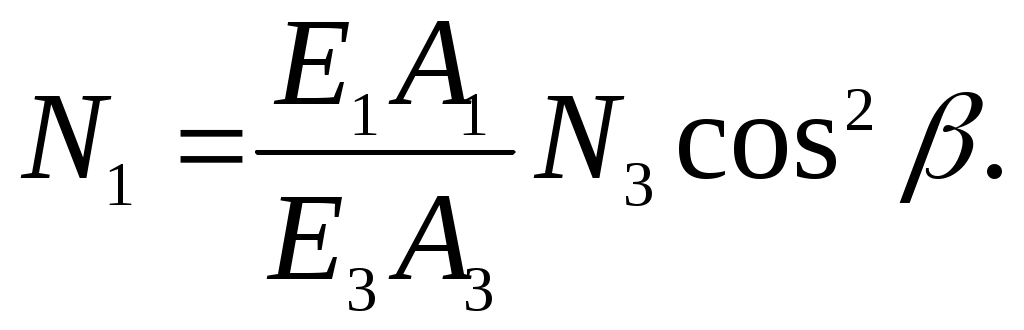 (9.8)
(9.8)
Подставим в (9.5) уравнение (9.8)
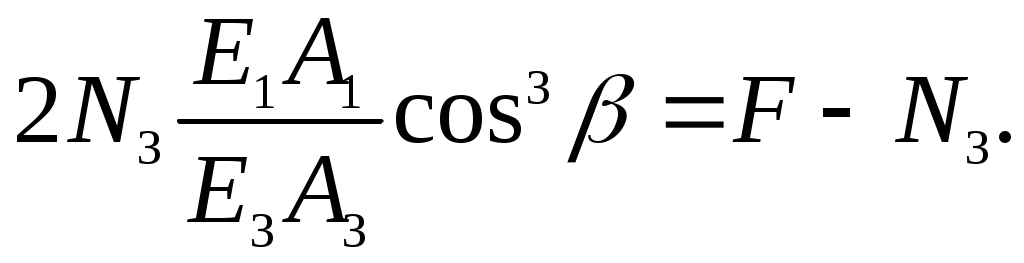
Отсюда
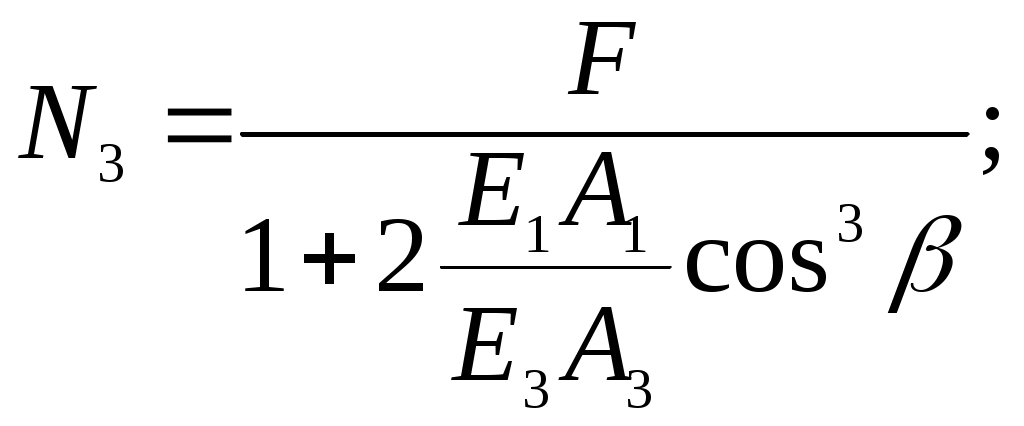
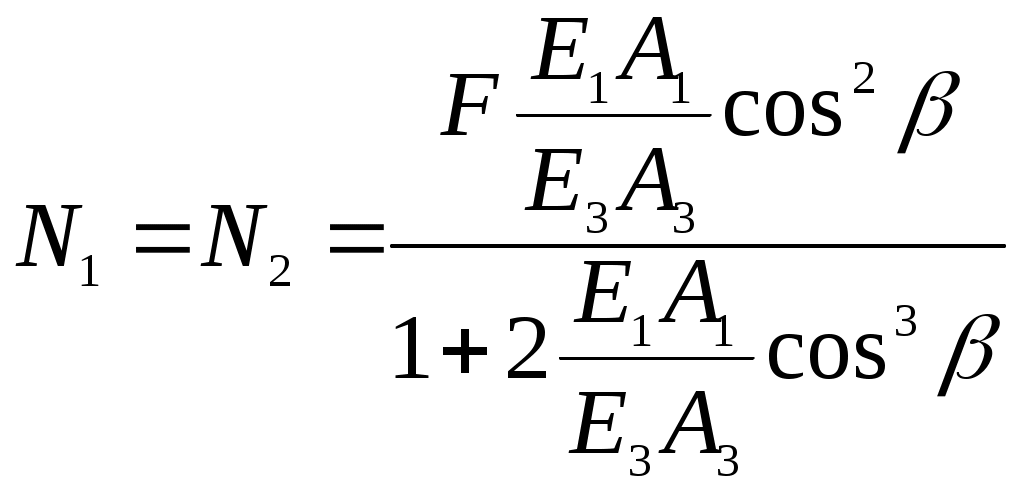 .
.
Одной из особенностей статически неопределимых систем является то, что усилия в них зависят от соотношения жесткостей отдельных элементов. Действительно, так как N3 иN1 зависят от соотношения Е1 А1 / Е 3 А3. Здесь Е1, Е3 – const, поэтому рассматривают отношение А1 /А3 .
При А1 /А3 0 N3F;
А1 /А3 0 N1 = N2.
Вывод будет такой: чем относительно жестче элемент статически неопределимой системы, тем большую долю внешней нагрузки, передаваемой на группу элементов, он принимает на себя.
9.1.1.2. Монтажные усилия
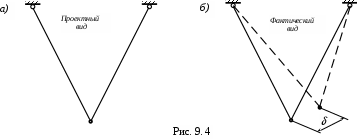
На рис. 9. 4,а задан проектный вид статически определимой системы, а на рис. 9. 4,б пунктиром представлен её фактический вид. Как видно из рисунков, при сборке неточно изготовленных по длине стержней в статически определённой системе никакие усилия не возникают, так как ничто не мешает перемещать и монтировать эти стержни до положения, соответствующего фактическим длинам стержней.
Иная картина наблюдается при неточности изготовления элементов статически неопределимых систем. Представим себе, что один из стержней такой системы (проектный вид её показан на рис.9. 5,а ), например средний, изготовлен на величину короче проектной длины (рис.9. 5,б). Для того чтобы соединить концы всех трех стержней в узле О, как это предусмотрено проектом, можно представить такую схему монтажа: средний стержень необходимо удлинить, а крайние укоротить (рис. 5,
в точке 1;
2. Затем силой F2 в точке 2.
Учтем, что мерой энергии является работа.
Тогда:
IIой –случай Статически загрузим балку сначала силой F2, а затем силой F1, получаем

Сравним оба значения U, получим
теорему о взаимности работ
Работа силы F1 на перемещениях, вызванных силой F2 , равна работе силы F2 на перемещениях, вызванных силой F1.
Частный случай при F1 = F2 , получим теорему о взаимности перемещений
v12= v21(8.24)
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
точки 2, вызнанный такой же силой, но приложенной в точке 1.
P.S.-теорему широко использует служба госгортехнадзора.
Вопросы для самопроверки
-
Какой принцип механики позволяет получить интеграл Мора для определения перемещений? -
Какие исходные данные требуются для вычисления перемещений по интегралу Мора? -
Как формулируется правило (способ) Верещагина для определения перемещений по эпюрам и всегда ли оно применимо? -
Что означает отрицательный знак, получаемый в конечном результате при определении перемещения по интегралу Мора или применении правила (способа) Верещагина? -
Что означает, если в пределах того или иного участка системы интеграл перемещении (или результат перемножения эпюр по способу Верещагина) обращается в нуль?
6. Почему теорему о взаимности перемещений широко использует служба Госгортехнадзора?
9. Простейшие статически неопределимые стержневые системы и балки
9.1. Статически неопределимые стержневые конструкции
Стержневая конструкция называется статически определимой, если в ней, при любом загружении, усилия во всех элементах могут быть определимы из одних уравнений статики.
Статически неопределимыми конструкциями (СНК) называются такие конструкции, в элементах которых усилия не могут быть определены при помощи только одних уравнений статики.
Кроме уравнений статики, для расчета статически неопределимых конструкций необходимо использовать уравнения, содержащие деформации элементов конструкции.
Все статически неопределимые конструкции имеют так называемые
«лишние» связи в виде закреплений, опор, т.к. при их отсутствии прочность и жесткость конструкции может оказаться необеспеченной. Лишними такие связи называются потому, что они не являются необходимыми для объяснения равновесия остальных элементов конструкции и её геометрической (кинематической) неизменяемости.
По условию прочности или жесткости конструкции «лишние» связи могут оказаться необходимыми.
Статически неопределимые конструкции, элементы которых работают на растяжение и сжатие, мы будем рассчитывать путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической стороны задачи.
При этом будем придерживаться следующего порядка.
-
Статическая сторона задачи. Составляем условия равновесия отсеченных элементов конструкций, содержащие неизвестные усилия. -
Геометрическая сторона задачи. Устанавливаем связь между деформациями отдельных элементов конструкции на основании условий совместности (согласованности) деформации. -
Физическая сторона задачи. На основании закона Гука выражаем деформацию элементов конструкции через действующие на неё неизвестные силы. В случае изменения температуры к деформациям, вызываемым неизвестными силами, добавляются деформации вследствие температурного удлинения. -
Синтез. Решаем уравнения статики совместно с уравнениями деформации, записанными в усилиях, и находим неизвестные усилия.
9.1.1. Статически неопределимые стержневые конструкции, работающие на растяжение и сжатие
9.1.1.1. Раскрытие статической неопределимости при помощи
уравнений совместности деформаций. Зависимости усилий от отношения жесткостей
Пример 1. Определим напряжение в призматическом стержне (EA=const), заделанном двумя концами, от силы F (рис. 9.1, а)
-
С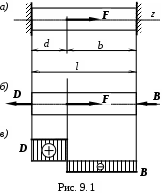 татическая сторона задачи. Освободим стержень от заделок, приложив по концам неизвестные реакции.
татическая сторона задачи. Освободим стержень от заделок, приложив по концам неизвестные реакции.
-D+F-B=0, (9.1)
D = F– B.
Две неизвестных реакции и одно уравнение статики, следовательно, задача один раз статически неопределима.
-
Геометрическая сторона задачи.
Так как концы стержня жестко закреплены, то длина его не изменяется:
l=0 . (9.2)
-
Физическая сторона задачи.
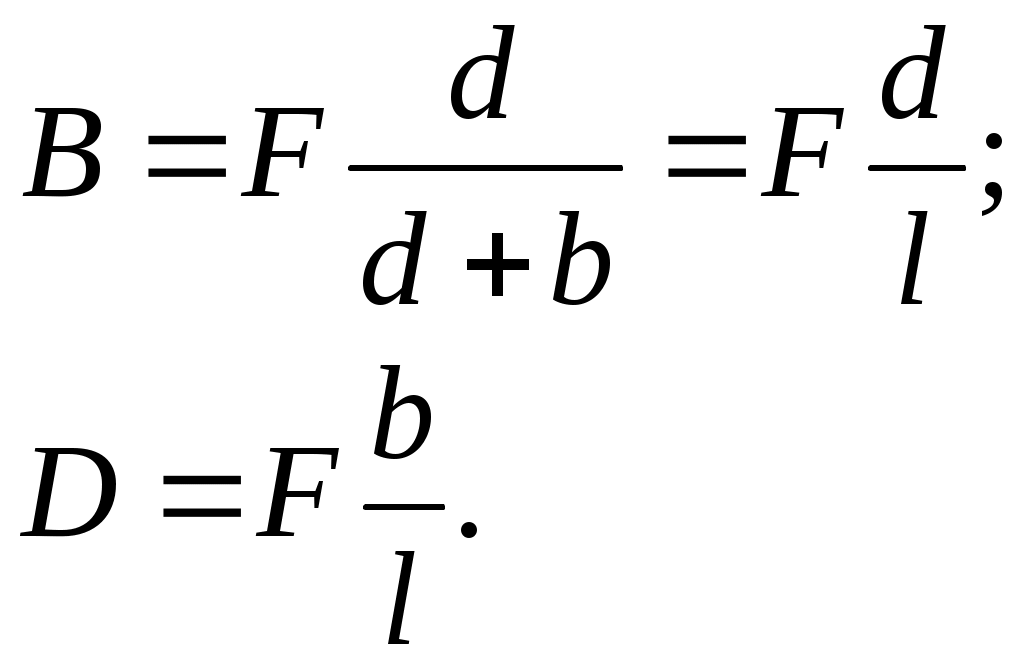
Строим эпюру внутренних сил (см. рис. 9.1, в).
Наибольшие напряжения равны
Для простоты рассуждения зададимся: d=l/3, b=2l/3. Тогда
Казалось бы, необходимо увеличить левое сечение в 2 раза.
Сделаем это: рассмотрим уравнение (9.3)
Получаем D=0.8F; B=0.2F.
D=0.4(F/A); B=0.2(F/A).
Видно, что увеличение площади одного из участков, ведет к перераспределению напряжения во всех элементах системы.
П

ример 2. Определить внутренние усилия в стальном стержне и бронзовой трубке, которые загружены усилием F через абсолютно твердую плиту, уложенную на них без зазора.
1. Z=0; NБР + NСТ - F=0.
2. lБР = lСТ.
3.
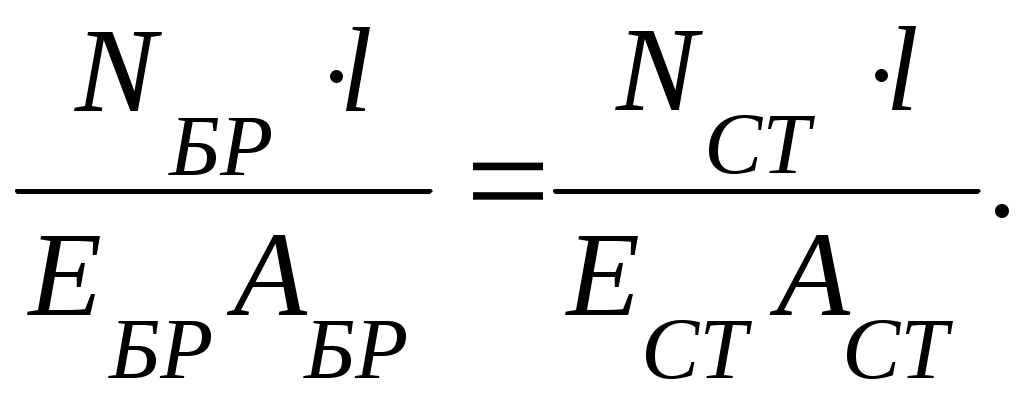
4.
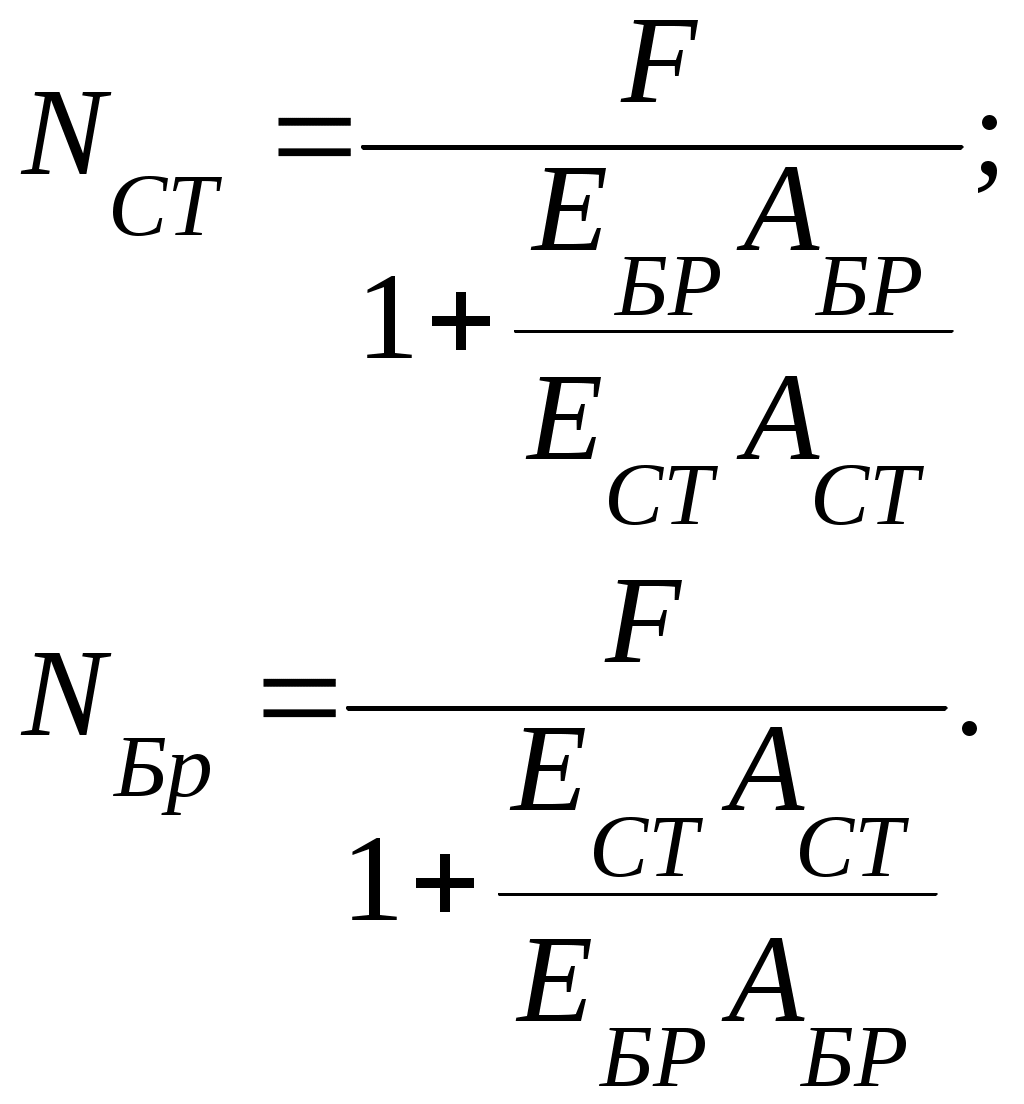
Распределение усилия зависит от отношения жесткостей отдельных элементов.
П

ример 3. Определить внутренние усилия в стержневой системе.
1. X=0; -N1sin + N2sin =0;
Y=0; N1cos +N3+ N2cos -F=0. (9.4)
Из первого уравнения N1= N2 ,
тогда из второго 2N1cos + N3 - F=0,
2. Под действием силы Fвсетри стержня растягиваются, во всех трех возникают деформации растяжения.
Растягивающие усилия в стержнях должны быть такими, чтобы соблюдалось согласование в деформациях (согласование в удлинениях). Согласование состоит в том, что после деформации, как и до неё, нижние концы всех трех стержней должны быть в одной точке.
Учитывая, что деформации малы, будем считать, что углы не изменяются. Тогда
l1 =l3cos . (9.6)
Уравнение (9.6) рассматривают как уравнение совместности деформации.
3.
4. Учтем , что l3 =l1cos, отсюда
Подставим в (9.5) уравнение (9.8)
Отсюда
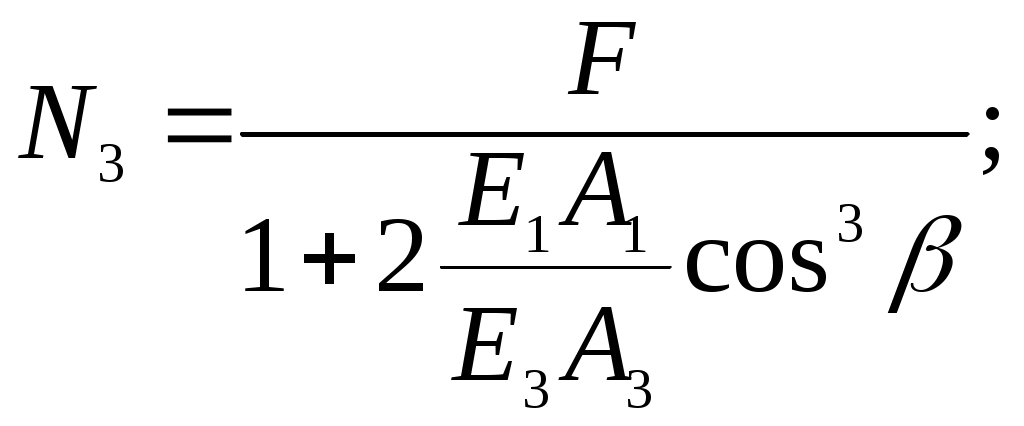
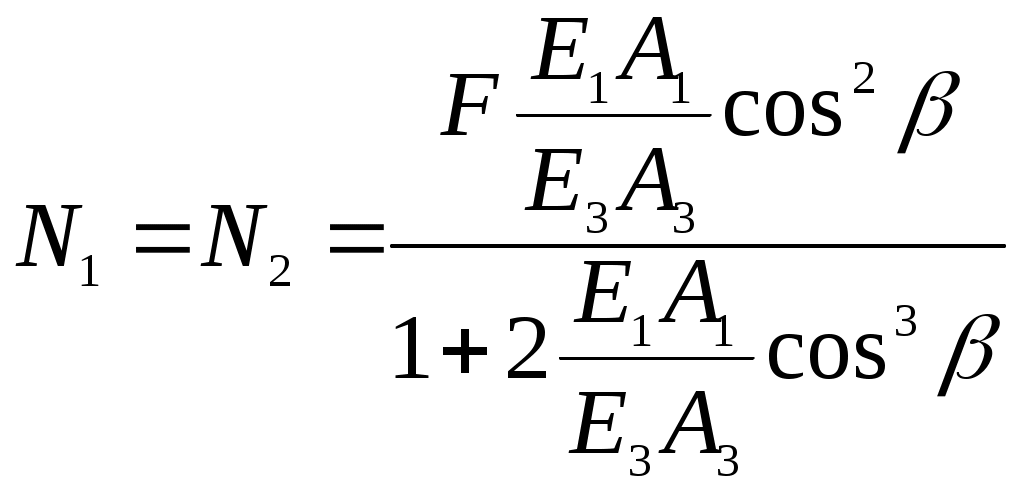 .
.Одной из особенностей статически неопределимых систем является то, что усилия в них зависят от соотношения жесткостей отдельных элементов. Действительно, так как N3 иN1 зависят от соотношения Е1 А1 / Е 3 А3. Здесь Е1, Е3 – const, поэтому рассматривают отношение А1 /А3 .
При А1 /А3 0 N3F;
А1 /А3 0 N1 = N2.
Вывод будет такой: чем относительно жестче элемент статически неопределимой системы, тем большую долю внешней нагрузки, передаваемой на группу элементов, он принимает на себя.
9.1.1.2. Монтажные усилия

На рис. 9. 4,а задан проектный вид статически определимой системы, а на рис. 9. 4,б пунктиром представлен её фактический вид. Как видно из рисунков, при сборке неточно изготовленных по длине стержней в статически определённой системе никакие усилия не возникают, так как ничто не мешает перемещать и монтировать эти стержни до положения, соответствующего фактическим длинам стержней.
Иная картина наблюдается при неточности изготовления элементов статически неопределимых систем. Представим себе, что один из стержней такой системы (проектный вид её показан на рис.9. 5,а ), например средний, изготовлен на величину короче проектной длины (рис.9. 5,б). Для того чтобы соединить концы всех трех стержней в узле О, как это предусмотрено проектом, можно представить такую схему монтажа: средний стержень необходимо удлинить, а крайние укоротить (рис. 5,