Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 391
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
в).
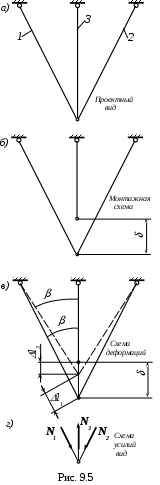
Таким образом, в статически неопределимой системе даже без внешней нагрузки, из-за одной лишь неточности изготовления отдельных элементов, в результате монтажа возникают усилия.
Для определения величины этих усилий используем, наряду с уравнениями статики, уравнения совместности деформаций, которое в рассматриваемом случае запишется в виде (рис. 5,в)
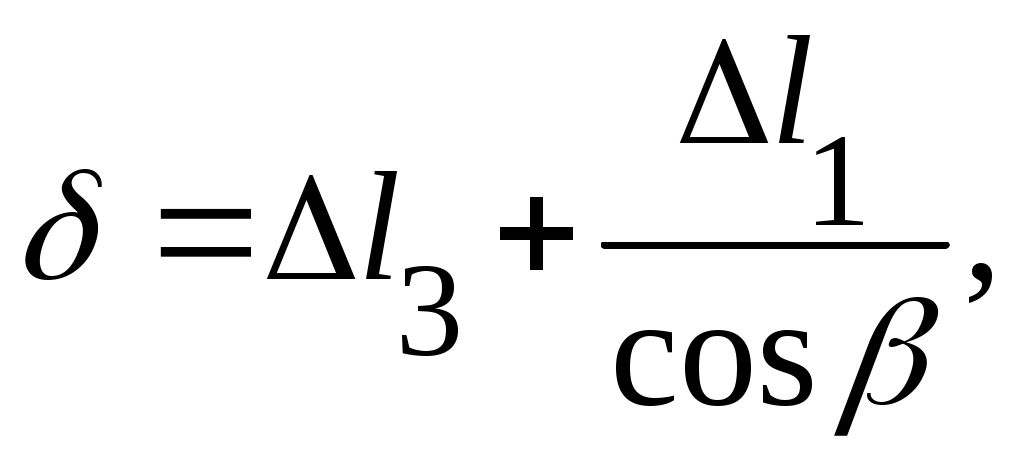
или, если принять указанные выше предположения о площадях поперечных
сечений и о материалах, из которых изготовлены стержни, то
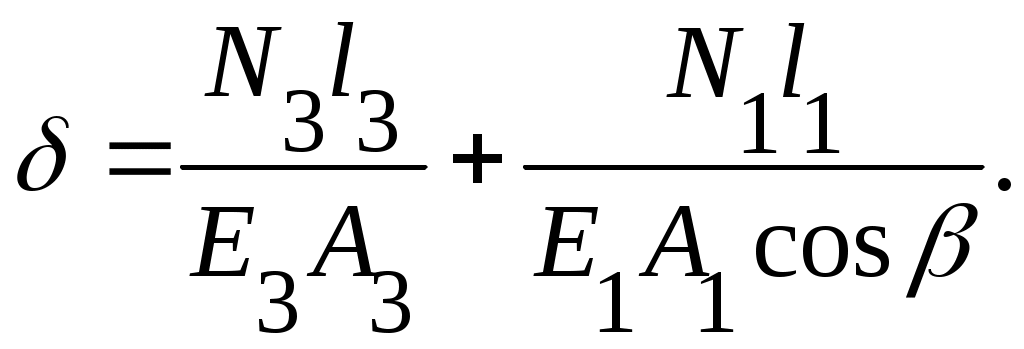 (9.9) Из условия статики (рис.9,г) находим:
(9.9) Из условия статики (рис.9,г) находим:
1)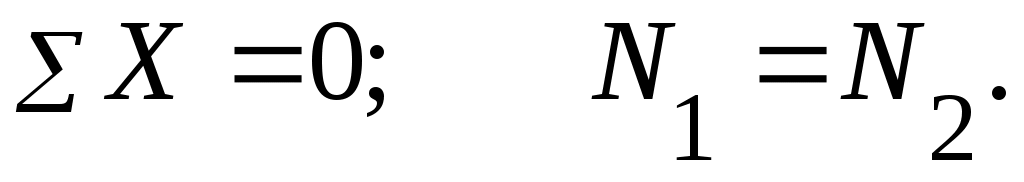 2)
2) 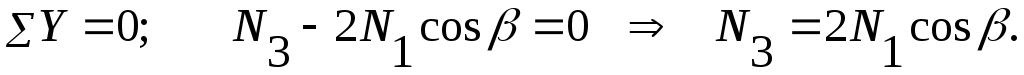 (9.10)
(9.10)
Подставляя N3 из (9.10) в (9.9), получим
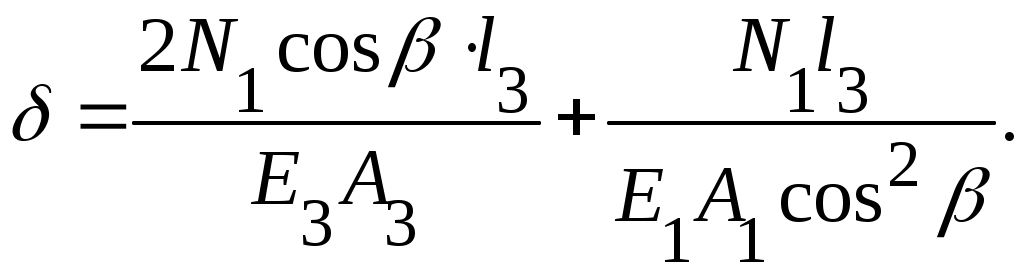
Отсюда
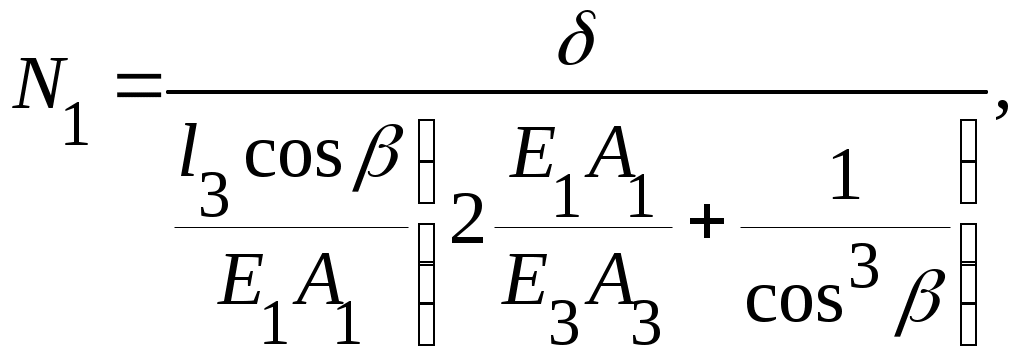 (9.11)
(9.11)
а если учесть (7), то
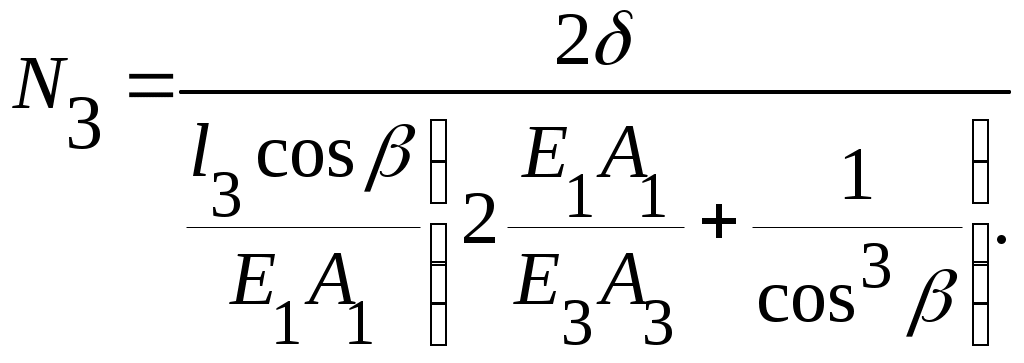 (9.12)
(9.12)

 9.1.1.3. Температурные усилия
9.1.1.3. Температурные усилия
Определим напряжения в призматическом брусе (ЕА=const), заделанном двумя концами, от равномерного нагрева всего бруса на t0C(рис.6). При повышении температуры брус стремится удлиниться и оказать давление на заделки, в которых возникнут реакции. Если отбросить одну из заделок (рис.6,б), тогда брус
с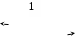
 вободно удлинится на величину
вободно удлинится на величину
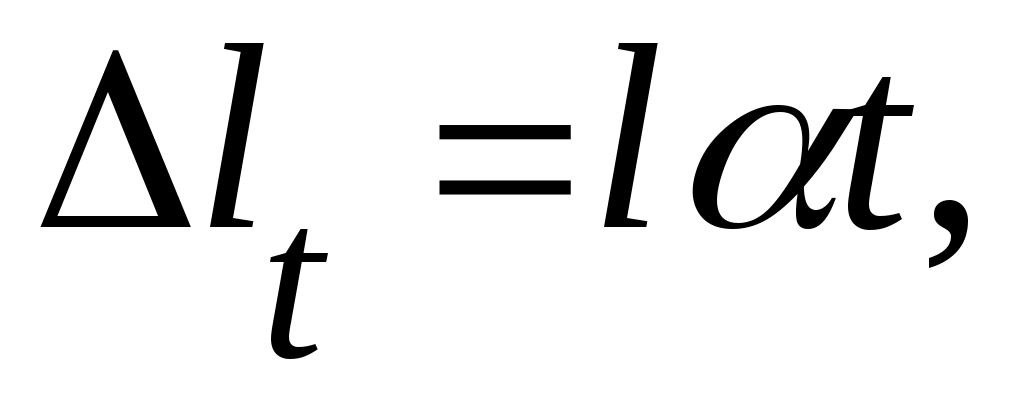 (9.13)
(9.13)
где - коэффициент линейного температурного расширения материала бруса.
Под действием внутренней силы N, равной опорным реакциям, брус должен сократиться на такую же величину; т.к. длина между заделками не может измениться, то
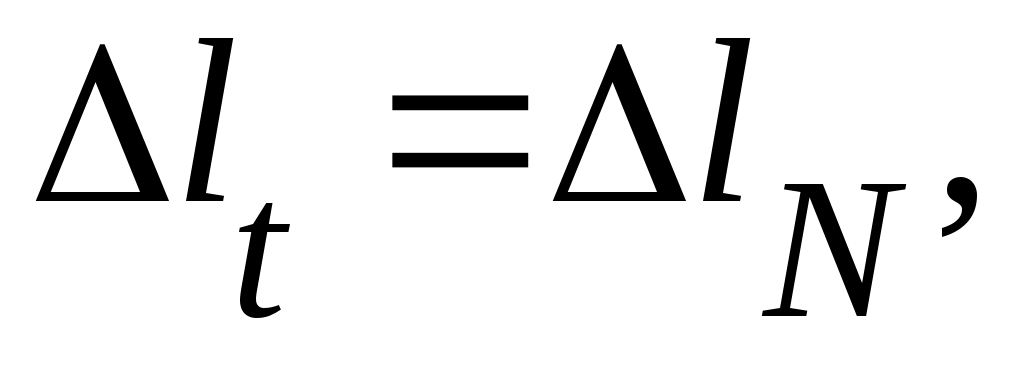
или
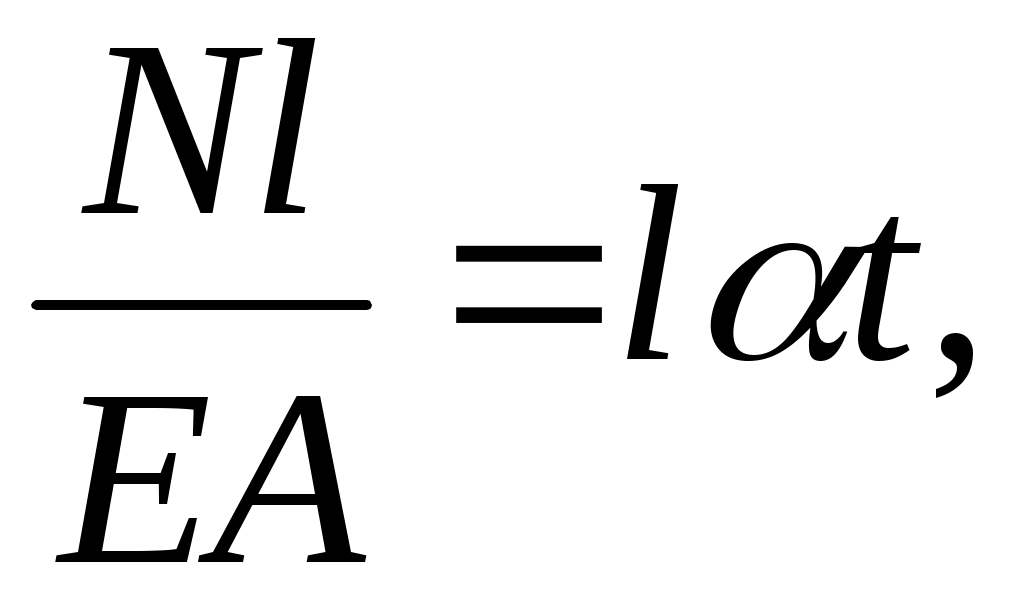
Отсюда
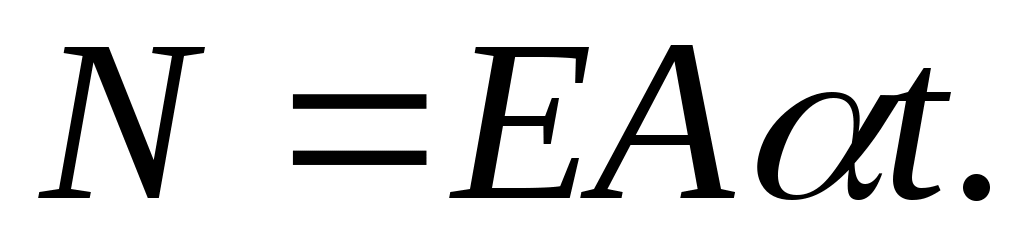
Нормальные температурные напряжения равны
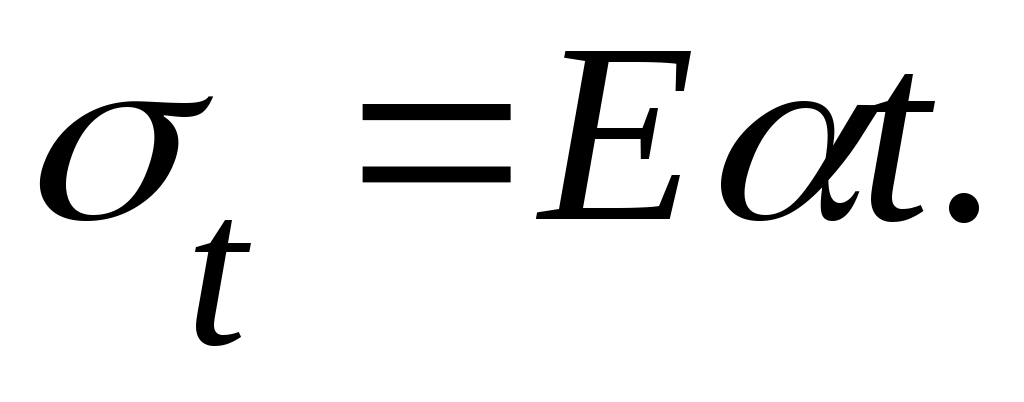 (9.14) Из (9.14) следует, что величина температурных напряжений тем больше, чем выше модуль продольной упругости и коэффициент линейного температурного расширения материала. При нагревании возникают сжимающие напряжения, а при охлаждении – растягивающие.
(9.14) Из (9.14) следует, что величина температурных напряжений тем больше, чем выше модуль продольной упругости и коэффициент линейного температурного расширения материала. При нагревании возникают сжимающие напряжения, а при охлаждении – растягивающие.
Из этого примера следует, что в статически неопределимых системах изменение температуры может вызвать дополнительные напряжения.
Пример 4. Биметаллическая пластина состоит из трех жестко связанных между собой листов одинаковых размеров(рис. 9.7), скрепленные абсолютно жесткими пластинами по торцам, средний из которых стальной, а крайние – медные.
Определить напряжения в медных и стальном листах, возникающие при равномерном нагревании пластины на t0 . Вычислить напряжения полагая
Ест = 200ГПа, Ем=100ГПа, ст=1,2510 -5град -1, м=1,6510 -5град -1, t0С=50.
NM=NCT ( 2MA=CTA)
CT= 2M .
2. Геометрическая сторона задачи.
СТ =М .
3. Физическая сторона задачи.
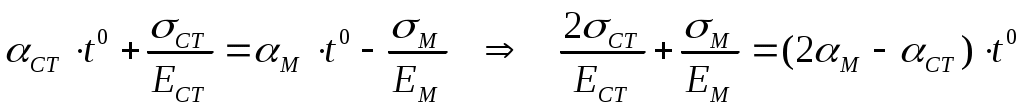
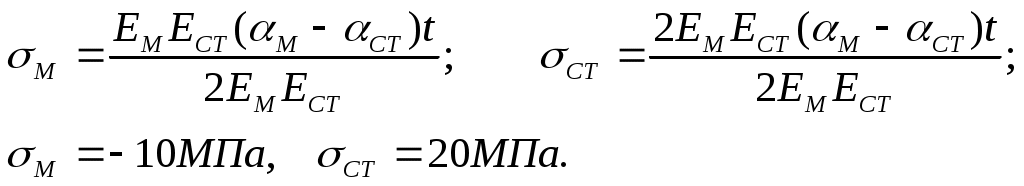
9.1.1.4. Усилие от независимого смещения опор
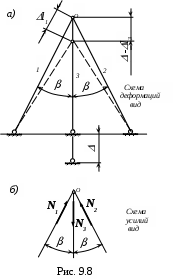
Рассмотрим статически неопределимую систему представленную
на рис. 9.8 Будем считать, что для всех стержней EA=constи изготовлены они из одного материала. Пускай средний стержень, сместился по отношению к другим так, как это показано на рис. 9.8, например, из-за размыва грунта вокруг фундамента под ним. Если нижний конец его получит перемещение на величину
, то верхний конец получит меньшее перемещение, так как он опирается на крайние стержни, которые препятствуют перемещаться концу среднего. Следовательно, средний стержень испытывает растяжение, и смещение верхнего конца его окажется таким: - l3.
Крайние стержни испытывают сжатие.
1. Из условия статики (рис. 9.8, б) находим:
1) 2)
2) 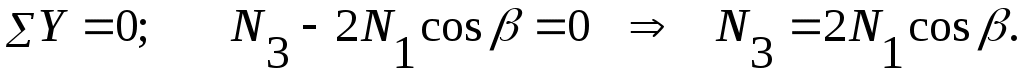
2. Уравнение совместности деформаций (рис. 9.8, а):
l1=(-l3)cos.
3. Физическая сторона задачи:
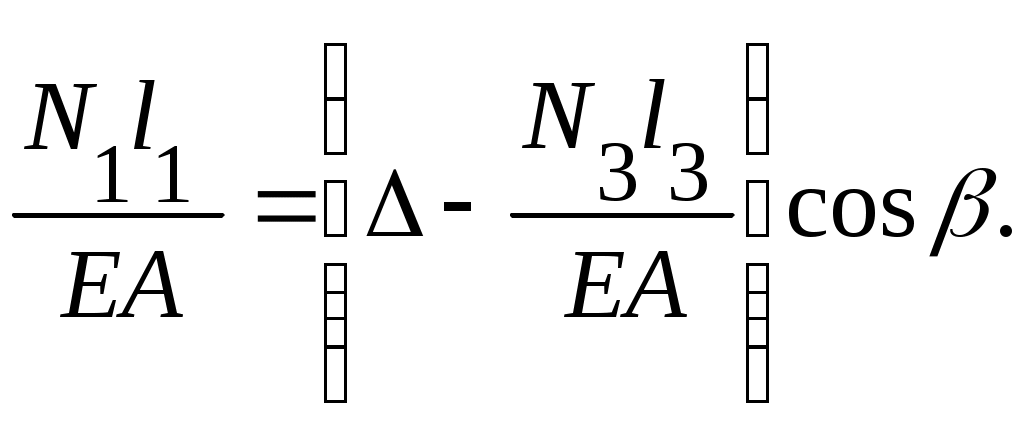
4.Синтез:
Учитывая, что N3=2N1cosи l3=l1cos, получим

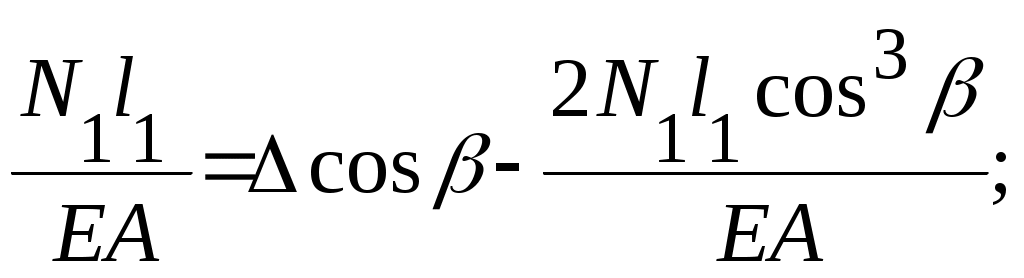
отсюда
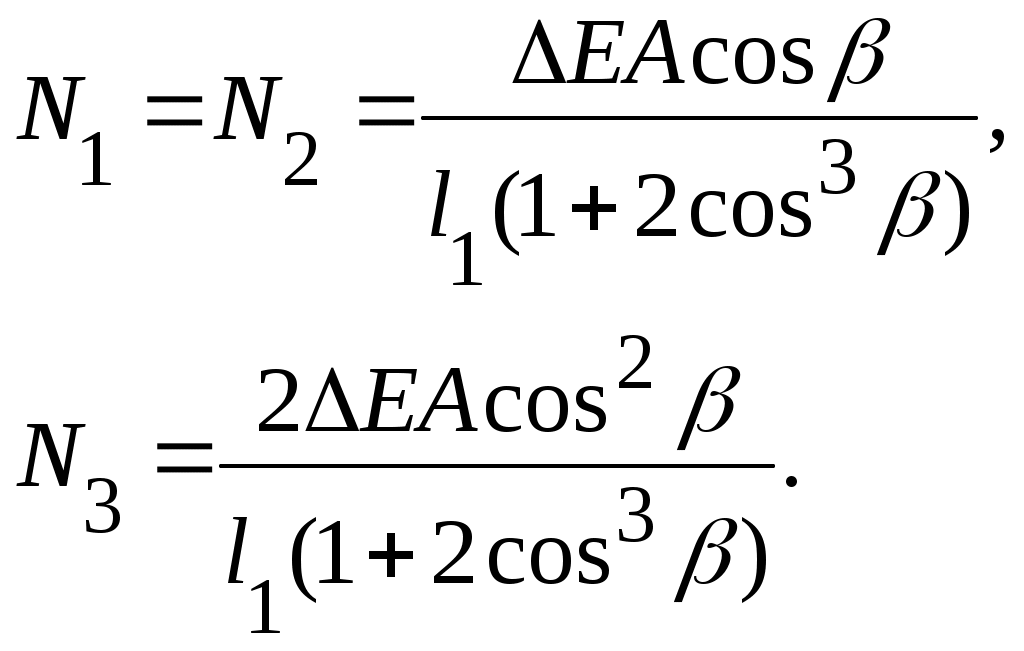
В статически неопределимых системах вследствие смещения опоры или опор, приводящего к изменению относительного расположения узлов, возникают усилия.
Этим объясняется то, что такие системы с большой осторожностью применяют в сооружениях при слабых грунтах.
9.1.2. Расчет по допускаемым напряжениям
В статически определимой системе все усилия находятся из одних уравнений статики и не зависят от соотношения жесткостей элементов. Поэтому после отыскания усилий в элементах системы, сечение каждого из элементов можно подобрать так, чтобы наибольшее напряжение в нем было равно допускаемому. Для этого, например, для фермы, достаточно площади поперечных сечений всех элементов определить по формуле
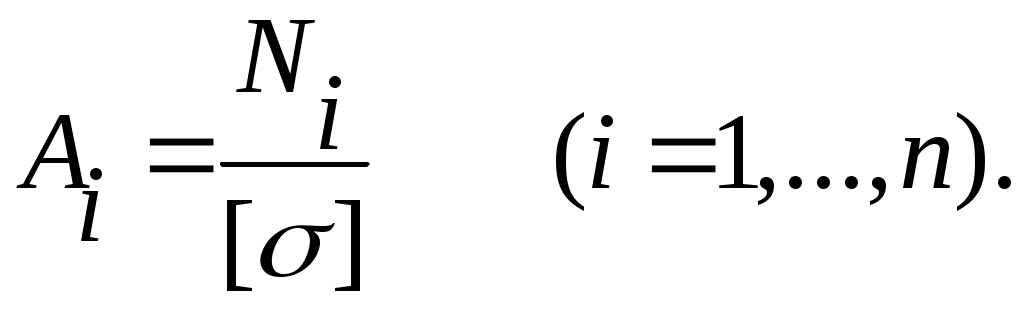
Здесь n – число элементов.
Таким образом, статически определимая ферма может быть запроектирована равнонапряженной, т.е. с одинаковыми по величине напряжениями во всех элементах, в частности равными допускаемым.
В случае статически неопределимых систем добиться равнонапряженности можно лишь в исключительных случаях. Покажем это на примере.
В примере 3 была рассмотрена статически неопределимая система и найдены усилия, возникающие в её элементах. Эти усилия зависят от соотношения жесткостей элементов.
Для простоты будем считать, что все три стержня изготовлены из одного материала и имеют одинаковые площади поперечных сечений. Таким образом, отношение жесткостей элементов равно единице. Усилия N1=N2 иN3 при этом изобразятся формулами
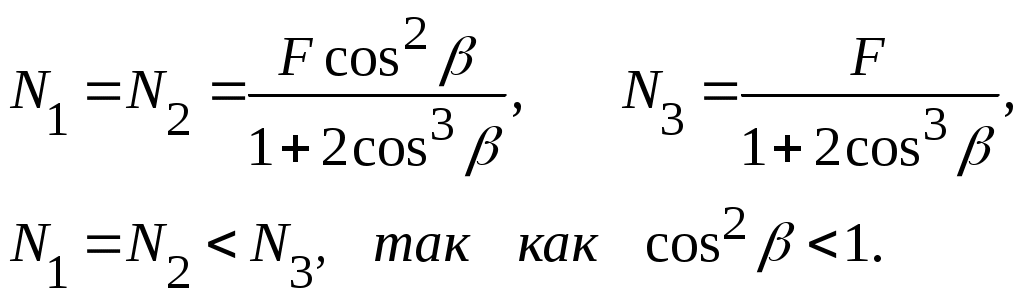 (9.15)
(9.15)
Подбираем по допускаемому напряжению сечение в элементе 3 с большим усилием:
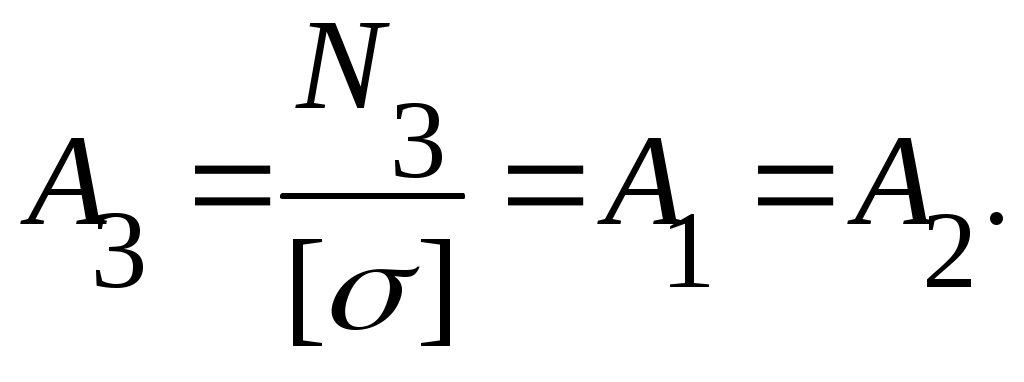
Напряжения же в элементах 1 и 2 оказывается меньше допускаемого:
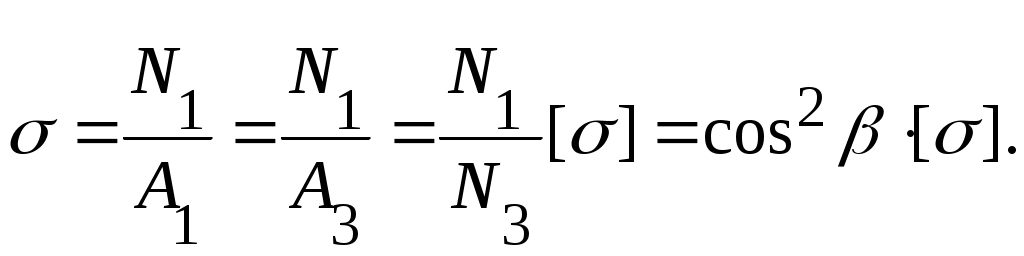
Выясним, не существует ли такого отношения площадей поперечных сечений элементов, при котором они могли бы быть равнонапряженными. Для того чтобы это было возможным, усилия должны находиться в таком же отношении, как и площади поперечных сечений соответствующих элементов.
Рассмотрим отношение усилий N1 и N3 , положив (Е1= Е2= Е3 =Е); будем иметь
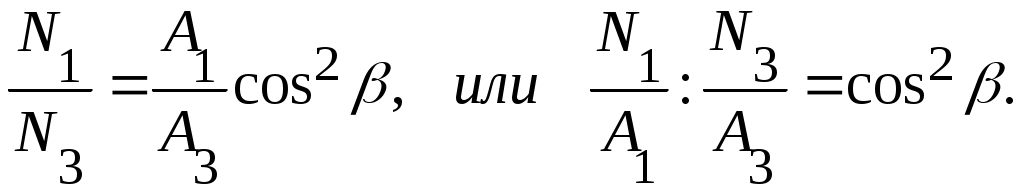
Если исходить из равнонапряженности элементов 1 и 3, получим
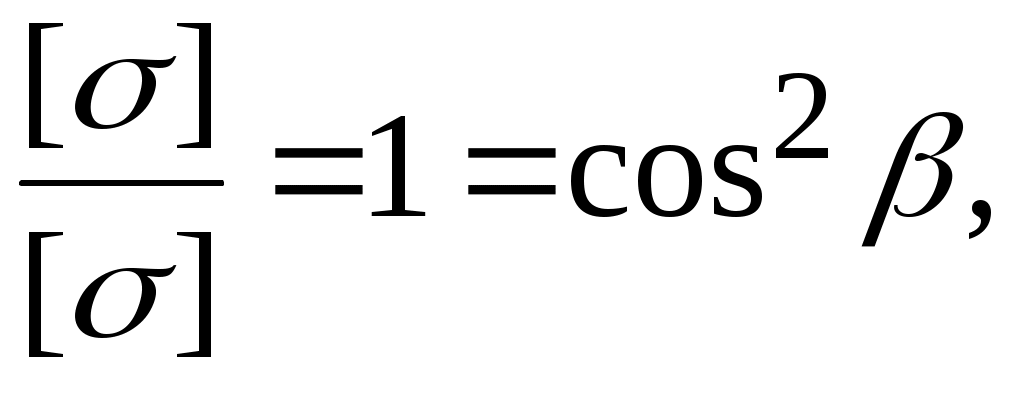
что противоречит виду системы, т.к. cos2=1 может выполняться лишь при =0, т.е. в случае, если все три стержня параллельны друг другу.
Если считать, что стержни выполнены из различных материалов, то
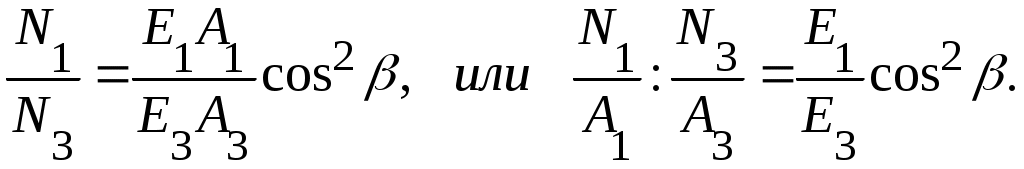
Учитывая целесообразность, поставим требование, чтобы
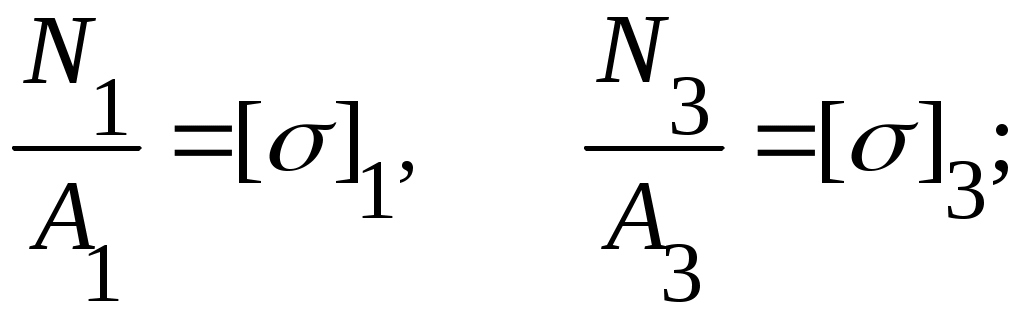
тогда получим
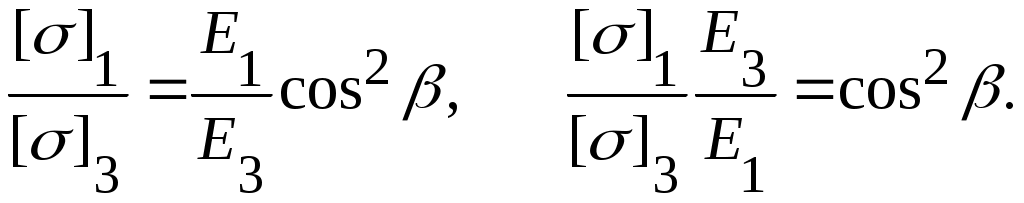
Полного использования материала за счет перебора ”Е” для каждого элементав статически неопределимой системе, можно добиться лишь в исключительных случаях.
9.1.3. Расчет по допускаемым нагрузкам
До сих пор, говоря об оценке надёжности (в смысле прочности) элемента, подвергнутого осевому действию сил, мы исходили из условия
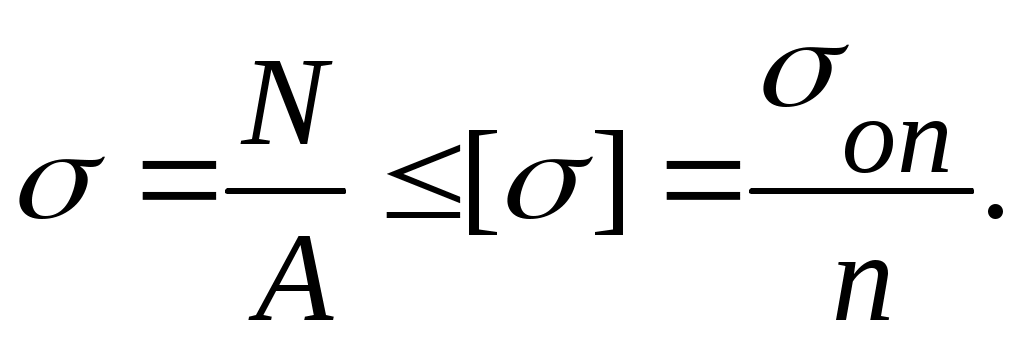
Такой подход к оценке прочности элемента составляет сущность расчета по допускаемым напряжениям.
Другим методом оценки прочности или подбора сечений элементов из условия прочности является так называемый
Таким образом, в статически неопределимой системе даже без внешней нагрузки, из-за одной лишь неточности изготовления отдельных элементов, в результате монтажа возникают усилия.
Для определения величины этих усилий используем, наряду с уравнениями статики, уравнения совместности деформаций, которое в рассматриваемом случае запишется в виде (рис. 5,в)
или, если принять указанные выше предположения о площадях поперечных
сечений и о материалах, из которых изготовлены стержни, то
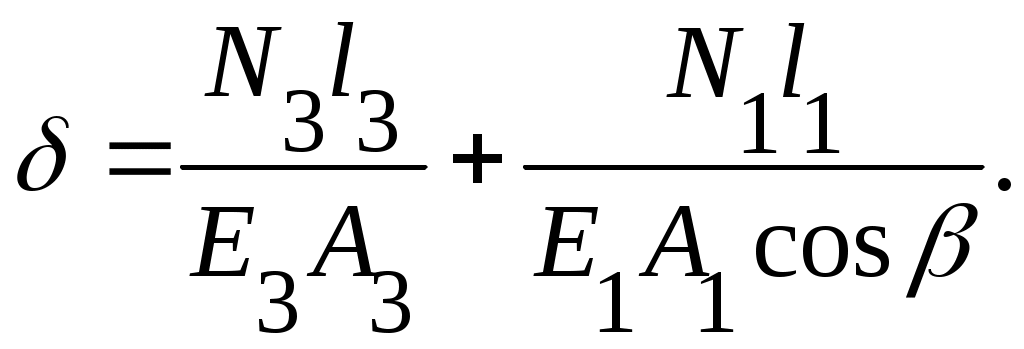 (9.9) Из условия статики (рис.9,г) находим:
(9.9) Из условия статики (рис.9,г) находим:1)
Подставляя N3 из (9.10) в (9.9), получим

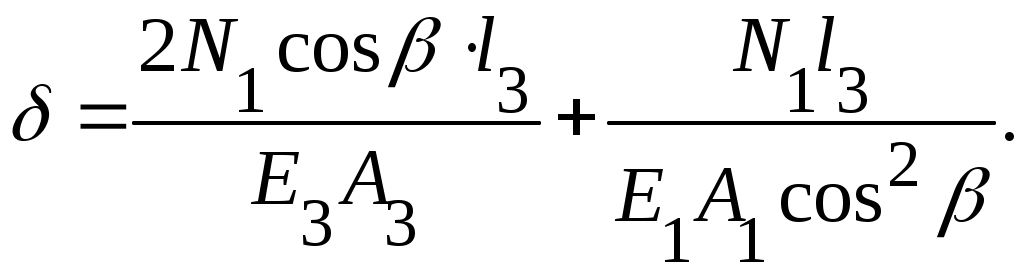
Отсюда
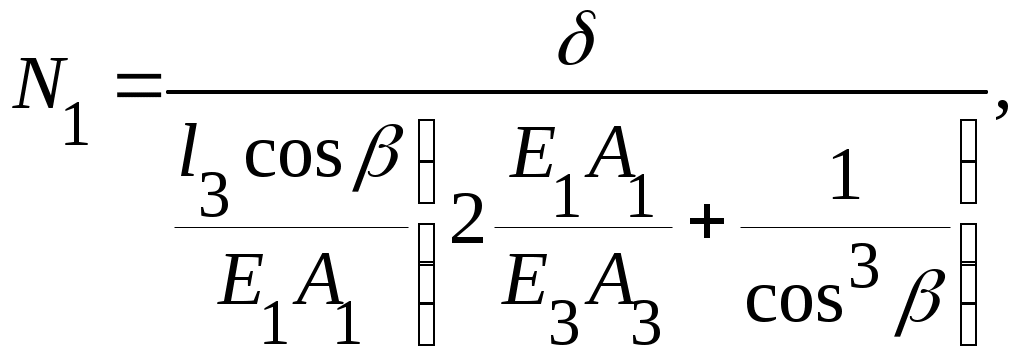 (9.11)
(9.11)а если учесть (7), то
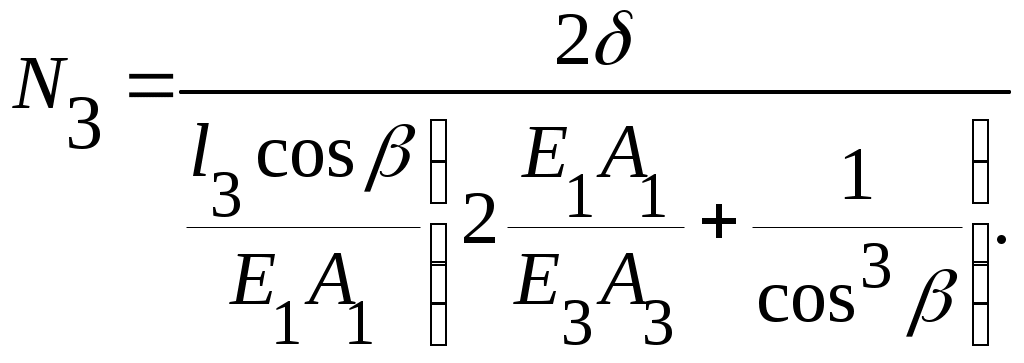 (9.12)
(9.12) 9.1.1.3. Температурные усилия
9.1.1.3. Температурные усилияОпределим напряжения в призматическом брусе (ЕА=const), заделанном двумя концами, от равномерного нагрева всего бруса на t0C(рис.6). При повышении температуры брус стремится удлиниться и оказать давление на заделки, в которых возникнут реакции. Если отбросить одну из заделок (рис.6,б), тогда брус
с
 вободно удлинится на величину
вободно удлинится на величинугде - коэффициент линейного температурного расширения материала бруса.
Под действием внутренней силы N, равной опорным реакциям, брус должен сократиться на такую же величину; т.к. длина между заделками не может измениться, то
или
Отсюда
Нормальные температурные напряжения равны
Из этого примера следует, что в статически неопределимых системах изменение температуры может вызвать дополнительные напряжения.
Пример 4. Биметаллическая пластина состоит из трех жестко связанных между собой листов одинаковых размеров(рис. 9.7), скрепленные абсолютно жесткими пластинами по торцам, средний из которых стальной, а крайние – медные.
Определить напряжения в медных и стальном листах, возникающие при равномерном нагревании пластины на t0 . Вычислить напряжения полагая
Ест = 200ГПа, Ем=100ГПа, ст=1,2510 -5град -1, м=1,6510 -5град -1, t0С=50.
-
С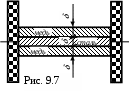 татика.
татика.
NM=NCT ( 2MA=CTA)
CT= 2M .
2. Геометрическая сторона задачи.
СТ =М .
3. Физическая сторона задачи.
-
Синтез.
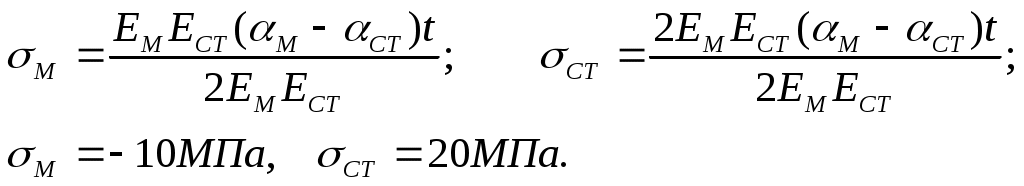
9.1.1.4. Усилие от независимого смещения опор
Рассмотрим статически неопределимую систему представленную
на рис. 9.8 Будем считать, что для всех стержней EA=constи изготовлены они из одного материала. Пускай средний стержень, сместился по отношению к другим так, как это показано на рис. 9.8, например, из-за размыва грунта вокруг фундамента под ним. Если нижний конец его получит перемещение на величину
, то верхний конец получит меньшее перемещение, так как он опирается на крайние стержни, которые препятствуют перемещаться концу среднего. Следовательно, средний стержень испытывает растяжение, и смещение верхнего конца его окажется таким: - l3.
Крайние стержни испытывают сжатие.
1. Из условия статики (рис. 9.8, б) находим:
1)

2. Уравнение совместности деформаций (рис. 9.8, а):
l1=(-l3)cos.
3. Физическая сторона задачи:
4.Синтез:
Учитывая, что N3=2N1cosи l3=l1cos, получим
отсюда
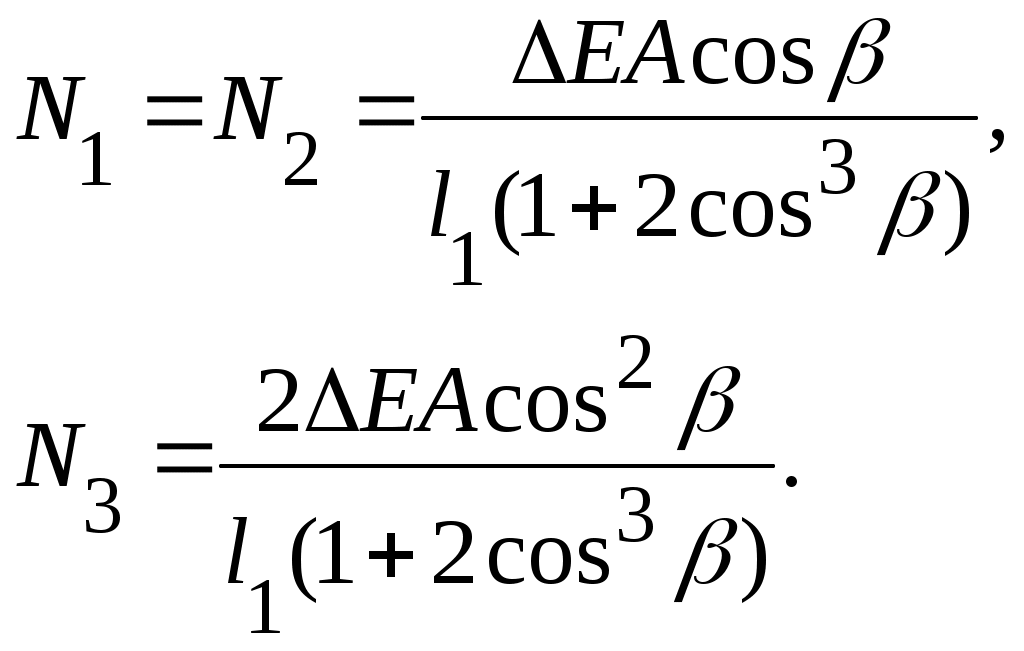
В статически неопределимых системах вследствие смещения опоры или опор, приводящего к изменению относительного расположения узлов, возникают усилия.
Этим объясняется то, что такие системы с большой осторожностью применяют в сооружениях при слабых грунтах.
9.1.2. Расчет по допускаемым напряжениям
В статически определимой системе все усилия находятся из одних уравнений статики и не зависят от соотношения жесткостей элементов. Поэтому после отыскания усилий в элементах системы, сечение каждого из элементов можно подобрать так, чтобы наибольшее напряжение в нем было равно допускаемому. Для этого, например, для фермы, достаточно площади поперечных сечений всех элементов определить по формуле
Здесь n – число элементов.
Таким образом, статически определимая ферма может быть запроектирована равнонапряженной, т.е. с одинаковыми по величине напряжениями во всех элементах, в частности равными допускаемым.
В случае статически неопределимых систем добиться равнонапряженности можно лишь в исключительных случаях. Покажем это на примере.
В примере 3 была рассмотрена статически неопределимая система и найдены усилия, возникающие в её элементах. Эти усилия зависят от соотношения жесткостей элементов.
Для простоты будем считать, что все три стержня изготовлены из одного материала и имеют одинаковые площади поперечных сечений. Таким образом, отношение жесткостей элементов равно единице. Усилия N1=N2 иN3 при этом изобразятся формулами
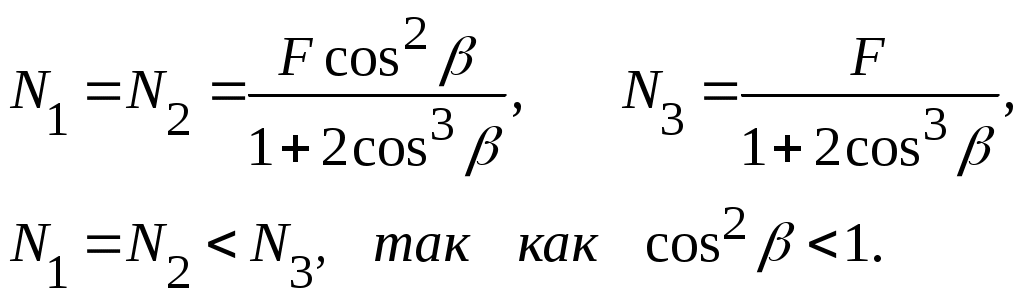 (9.15)
(9.15)Подбираем по допускаемому напряжению сечение в элементе 3 с большим усилием:
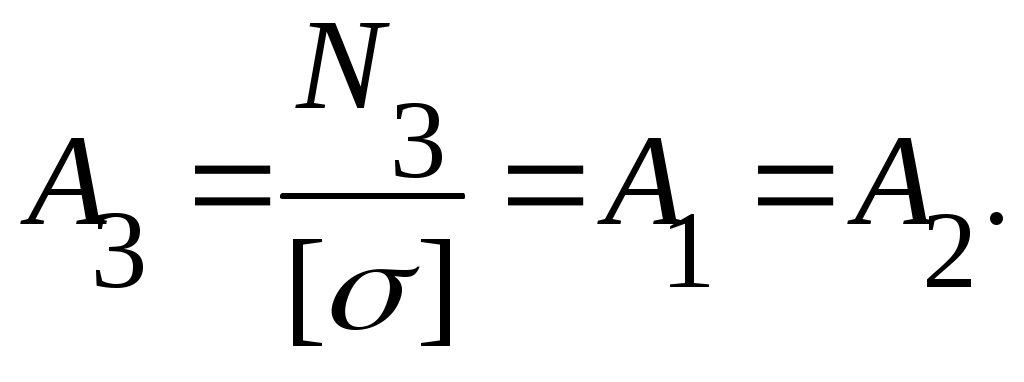
Напряжения же в элементах 1 и 2 оказывается меньше допускаемого:
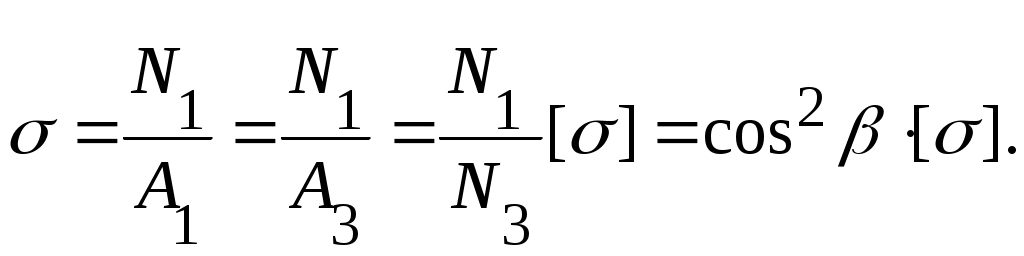
Выясним, не существует ли такого отношения площадей поперечных сечений элементов, при котором они могли бы быть равнонапряженными. Для того чтобы это было возможным, усилия должны находиться в таком же отношении, как и площади поперечных сечений соответствующих элементов.
Рассмотрим отношение усилий N1 и N3 , положив (Е1= Е2= Е3 =Е); будем иметь
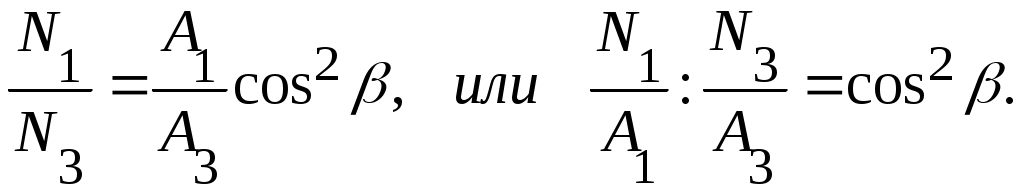
Если исходить из равнонапряженности элементов 1 и 3, получим
что противоречит виду системы, т.к. cos2=1 может выполняться лишь при =0, т.е. в случае, если все три стержня параллельны друг другу.
Если считать, что стержни выполнены из различных материалов, то
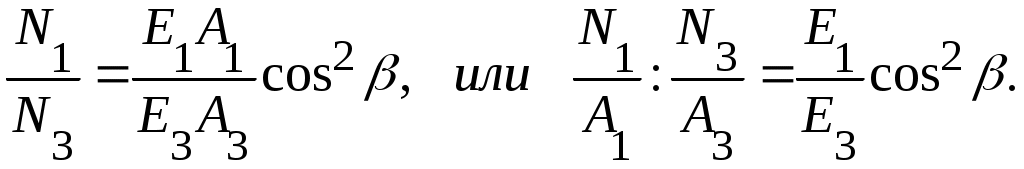
Учитывая целесообразность, поставим требование, чтобы
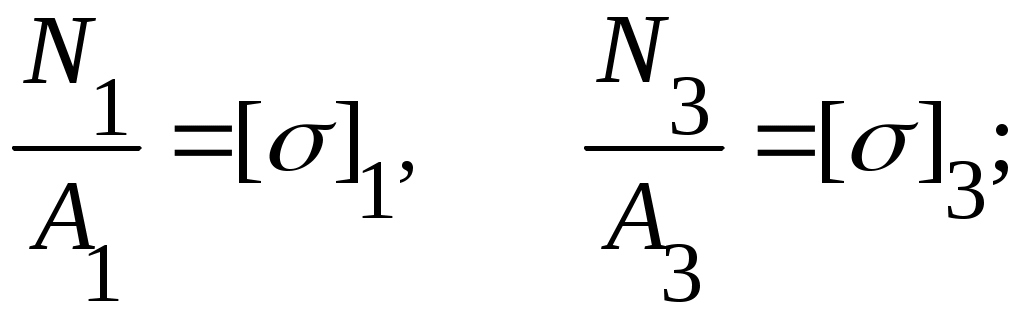
тогда получим
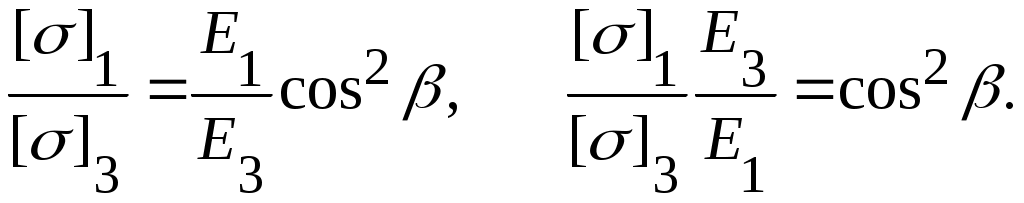
Полного использования материала за счет перебора ”Е” для каждого элементав статически неопределимой системе, можно добиться лишь в исключительных случаях.
9.1.3. Расчет по допускаемым нагрузкам
До сих пор, говоря об оценке надёжности (в смысле прочности) элемента, подвергнутого осевому действию сил, мы исходили из условия
Такой подход к оценке прочности элемента составляет сущность расчета по допускаемым напряжениям.
Другим методом оценки прочности или подбора сечений элементов из условия прочности является так называемый