Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 389
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
метод расчета по допускаемым нагрузкам. Сущность его рассмотрим на примере 3 (рис. 3,а). Для упрощения анализа будем считать Е1= Е3= Е и А1=А3=А.
Проследим за характером работы системы в процессе постепенного возрастания силы F. Пусть зависимость () описывается диаграммой Прандтля (рис. 8) для идеального упруго-пластичного материала.
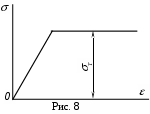 Помним, что усилия в среднем стержне больше, чем в крайних, следовательно, в нем большими оказываются и напряжения. До тех пор, пока напряжения в среднем стержне не достигли предела текучести, усилия во всех стержнях изменяются пропорционально силе Fи определяются формулой ( 9.15). Как только в среднем стержне напряжения достигнут предела текучести, дальнейший рост силы Fне будет сопровождаться увеличением напряжений в среднем стержне; расти будут лишь напряжения в крайних стержнях, не достигших ещё предела текучести.
Помним, что усилия в среднем стержне больше, чем в крайних, следовательно, в нем большими оказываются и напряжения. До тех пор, пока напряжения в среднем стержне не достигли предела текучести, усилия во всех стержнях изменяются пропорционально силе Fи определяются формулой ( 9.15). Как только в среднем стержне напряжения достигнут предела текучести, дальнейший рост силы Fне будет сопровождаться увеличением напряжений в среднем стержне; расти будут лишь напряжения в крайних стержнях, не достигших ещё предела текучести.
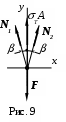 Возникновение напряжений в среднем стержне, равных пределу текучести, не означает, что узел О может перемещаться без возрастания силы F, так как опусканию узла О препятствуют крайние стержни, в которых напряжения ещё не достигли предела текучести. Таким образом, пластическая деформация среднего стержня задерживается крайними. Поэтому возникновение в среднем стержне напряжений, равных пределу текучести, ещё не является опасным для системы. Система ещё способна продолжать сопротивляться возрастающей нагрузке.
Возникновение напряжений в среднем стержне, равных пределу текучести, не означает, что узел О может перемещаться без возрастания силы F, так как опусканию узла О препятствуют крайние стержни, в которых напряжения ещё не достигли предела текучести. Таким образом, пластическая деформация среднего стержня задерживается крайними. Поэтому возникновение в среднем стержне напряжений, равных пределу текучести, ещё не является опасным для системы. Система ещё способна продолжать сопротивляться возрастающей нагрузке.
Начиная с момента, когда в среднем стержне возникают напряжения Т, система перестает быть статически неопределимой, так как усилие в среднем стержне приобретает определенное значение Т А и не меняется при дальнейшем увеличении силы F. Усилия в крайних стержнях определяются из уравнений равновесия (рис. 9)
X=0; -N1sin + N2sin =0;
Y=0; N1cos +ТА + N2cos -F=0. (9.16)
Из первого уравнения N1= N2 ,
Тогда из второго 2N1cos +ТА - F=0
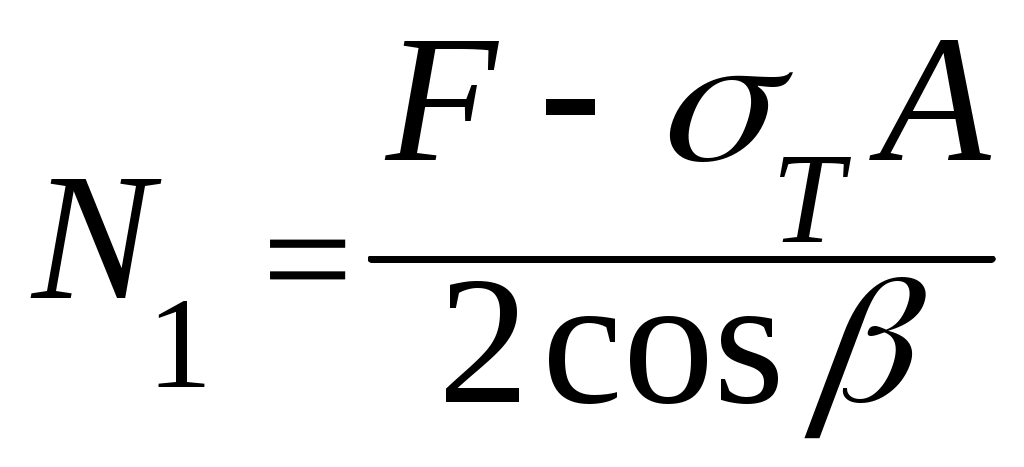
(9.17)
Нагрузка, при которой возникают напряжения Т в среднем стержне может быть обозначена FТ ; её находим из условия
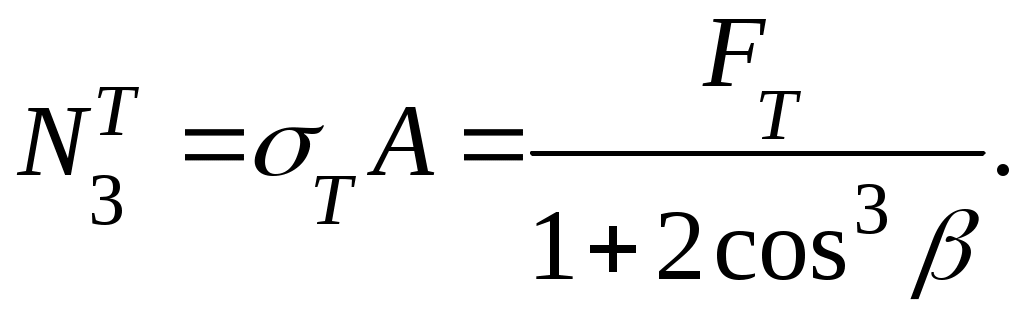
Дальнейший рост нагрузки приводит к тому, что и в крайних стержнях напряжения достигают предела текучести. При соответствующем значении нагрузки, которое обозначим Fоп , происходить опускание узла О без дальнейшего увеличения её. То есть система (все её элементы) будет испытывать возрастающие пластические деформации при постоянной нагрузке. Сила Fоп, которой соответствует возникновение опасного состояния системы, может быть найдено из равенства (9.17), если в нем положить N1 = Т А, т.е.
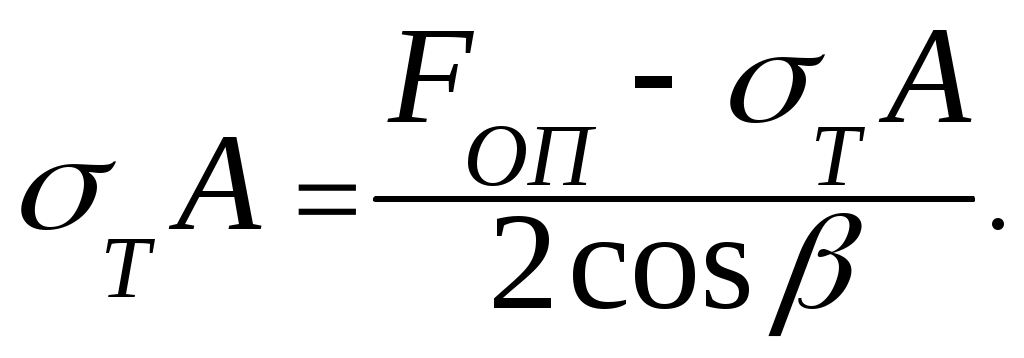
Отсюда
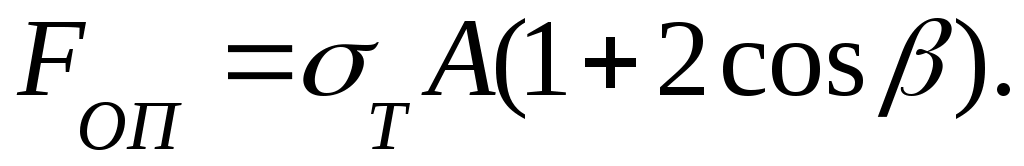
Нагрузка FТ , при которой впервые в системе возникают напряжения ( в среднем стержне), равные Т , меньше нагрузки Fоп , соответствующей возникновению опасного состояния системы:
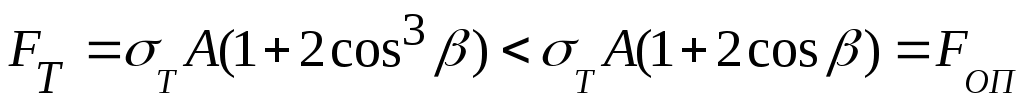 .
.
Расчет по допускаемому напряжению сводится к условию прочности:
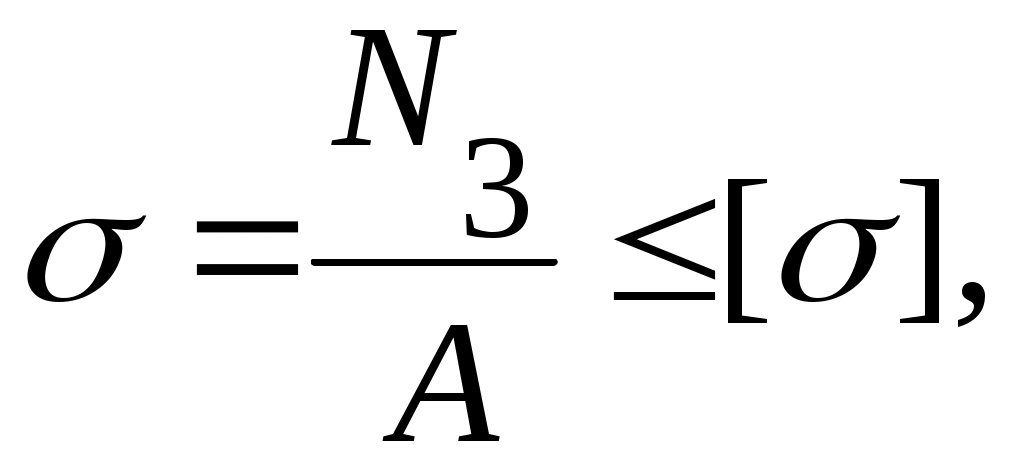
откуда
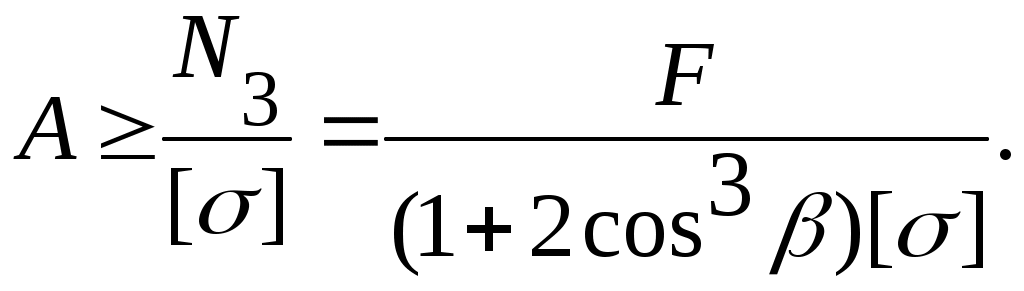 (9.18)
(9.18)
При расчете по допускаемой нагрузке ставим условие, чтобы фактическая нагрузка F не была больше так называемой допускаемой:
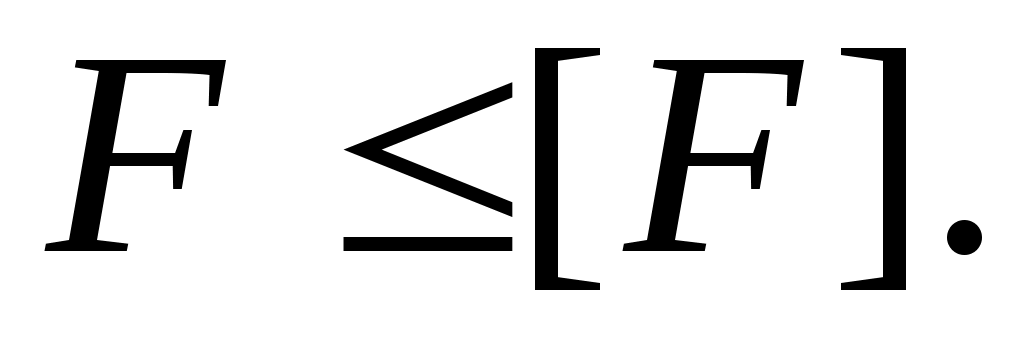
Величину допускаемой нагрузки находим по формуле
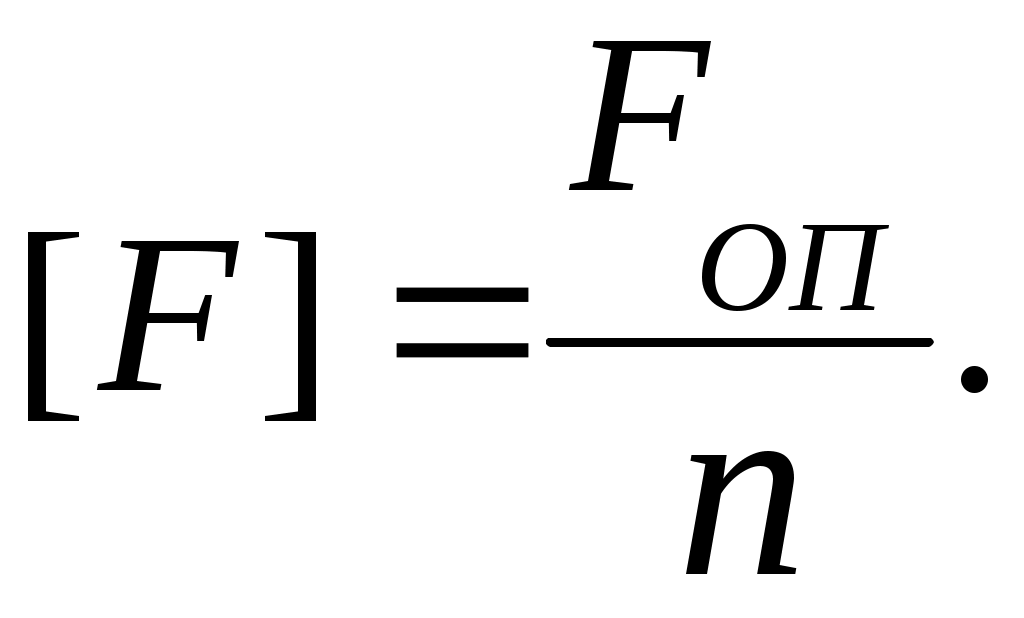 (9.19)
(9.19)
Если принять коэффициент запаса прочности n таким же, как при определении [], получим
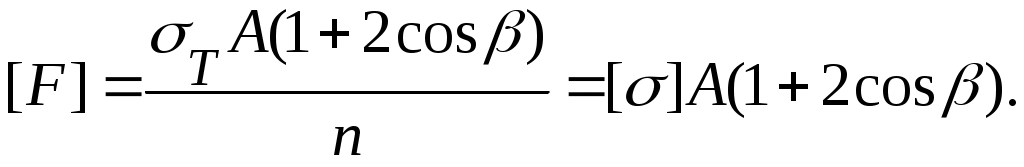
Условие прочности по допускаемой нагрузке в данном случае имеет вид
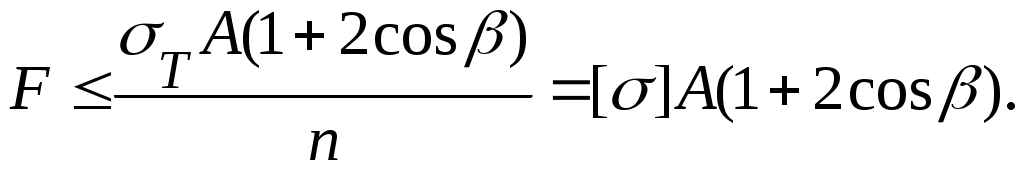
Площадь поперечного сечения стержней по допускаемой нагрузке
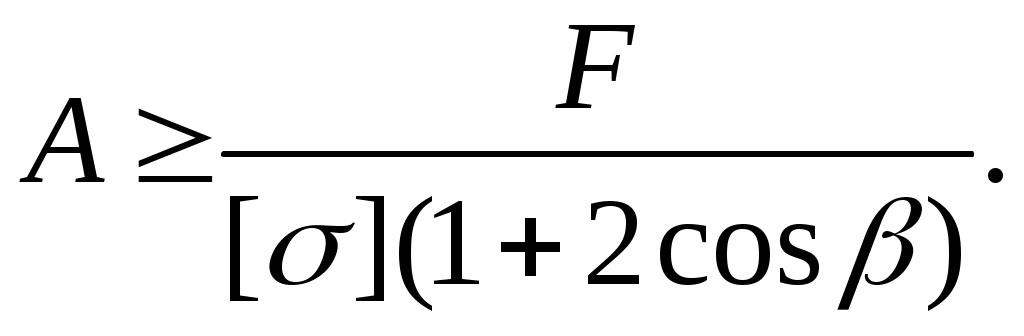
(9.20)
Сопоставляя формулы (9.18) и (9.20), легко обнаруживаем большую экономичность расчета по допускаемым нагрузкам при сравнении его с расчетом по допускаемым напряжениям.
Действительно, если положить, например, что =300 (cos= 3 2), то по допускаемому напряжению будем иметь
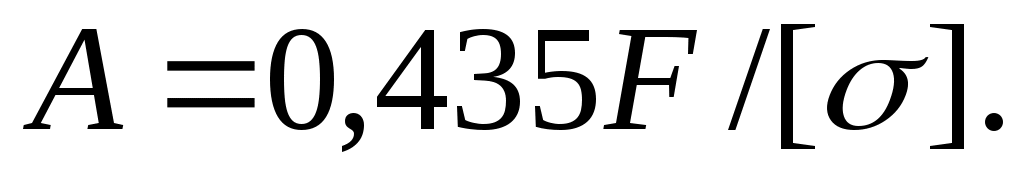
Производя аналогичную операцию по допускаемой нагрузке, получим
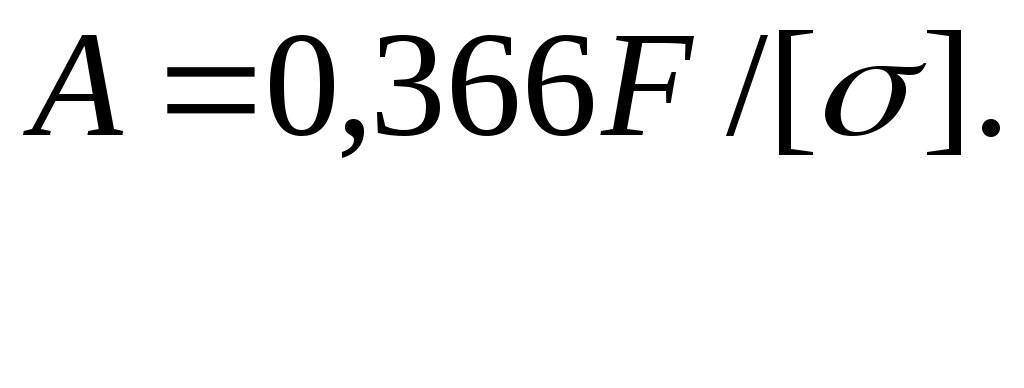
Перерасход материала при расчете по допускаемому напряжению составил 19% по сравнению с расчетом по допускаемой нагрузке.
9.1.4. Пример выполнения домашнего задания
Содержание задания:
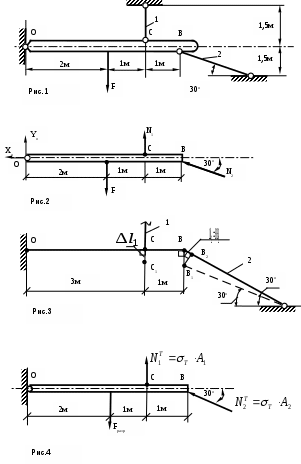
Абсолютно жестким брус ОВ поддерживается с помощью стальных стержней 1, 2. Площади поперечных сечений: А1=10 см2, А2=6см2. Допускаемое напряжение материала стержней [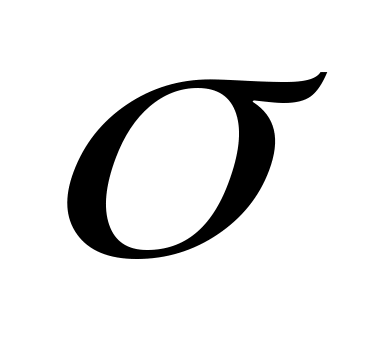 ]=160 МПа. Определить допускаемую силу [F] из расчета по допускаемым напряжениям и по разрушающей нагрузке.
]=160 МПа. Определить допускаемую силу [F] из расчета по допускаемым напряжениям и по разрушающей нагрузке.
Начертим заданную схему в масштабе и проставим размеры в системе СИ (см. рис. 1).
Решение
1. Определение допускаемой силы
Освободимся от связей, наложенных на брус ОВ (см. рис. 2). Для полученной плоской системы сил можно составить три независимых уравнения равновесия статики
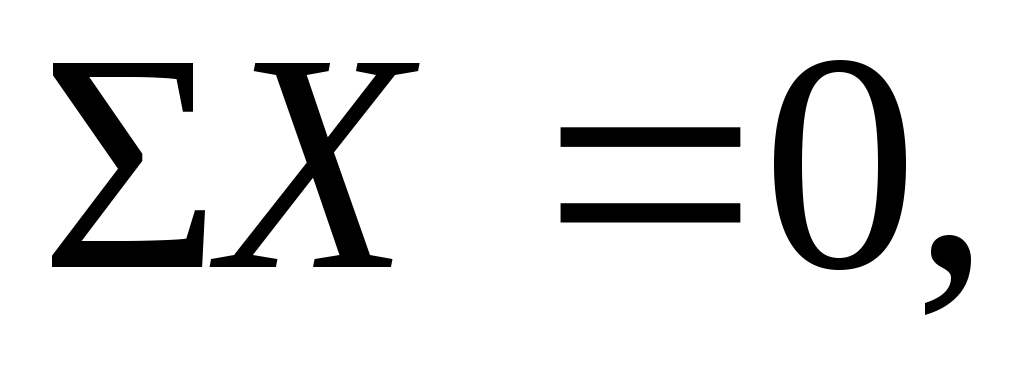
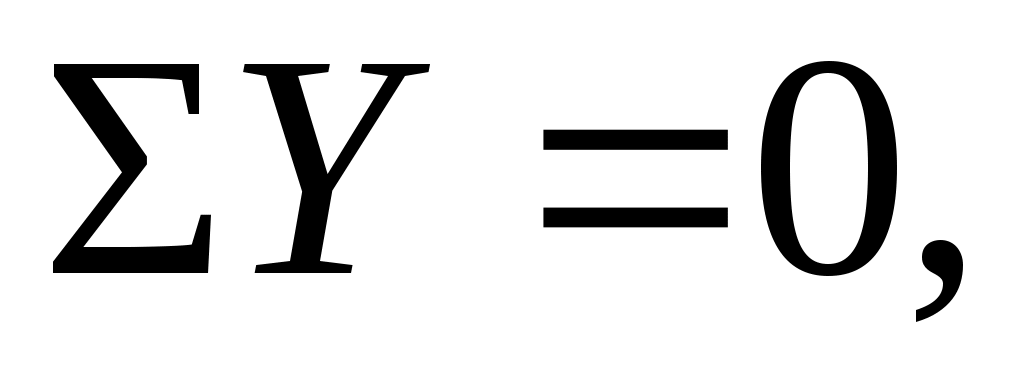
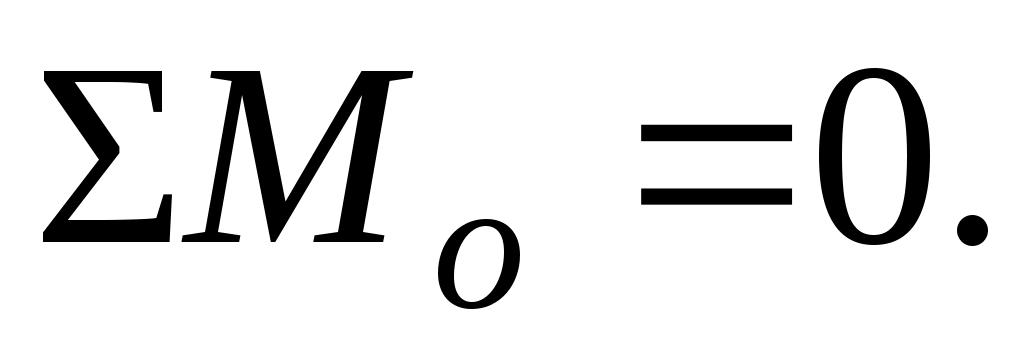
Неизвестных усилий – четыре. Таким образом, степень статической неопределимости
n=4нз-3ур=1раз.. статически неопределимая задача.
Для записи условия прочности нам необходимо знать усилия в стержнях 1,2 и совсем не обязательно знать реакции в опоре.
Дальнейшее решение задачи по плану для СНЗ.
1.1. Статическая сторона задачи (см. рис. 2).
 Мо=0; -F 2+
Мо=0; -F 2+
N1 3+ N2sin300=0,
откуда 3N1+2N2=2F. (1)
1.2. Геометрическая сторона задачи
Для составления уравнения совместности деформации покажем систему в деформированном состоянии (см. рис. 3). В результате деформации стержней 1,2 брус ОВ повернется вокруг опоры О, точки В и С перейдут в положение В1 и С1 (см. рис. 3). Как видно из рис.3,
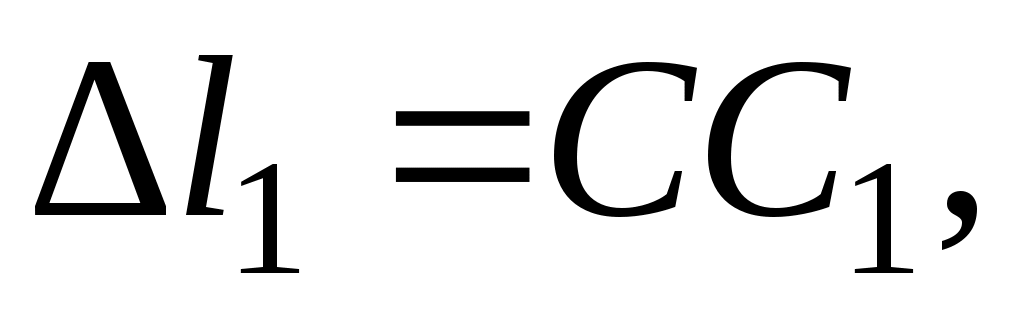
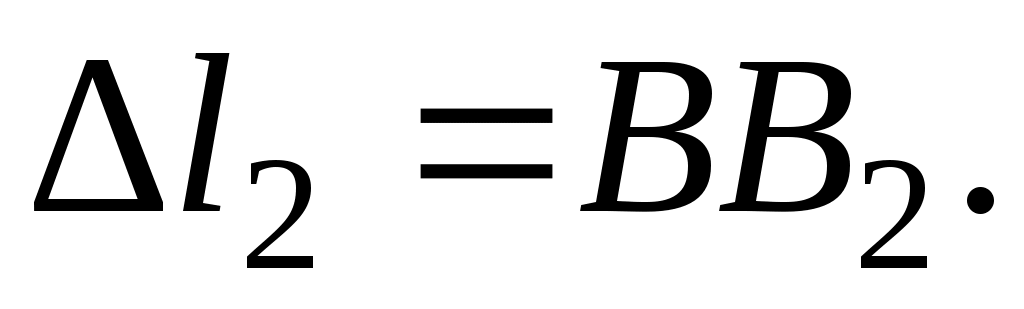
Соотношение между деформациями стержней получим из подобия треугольников
 ОСС1
ОСС1
 ОВВ1
ОВВ1
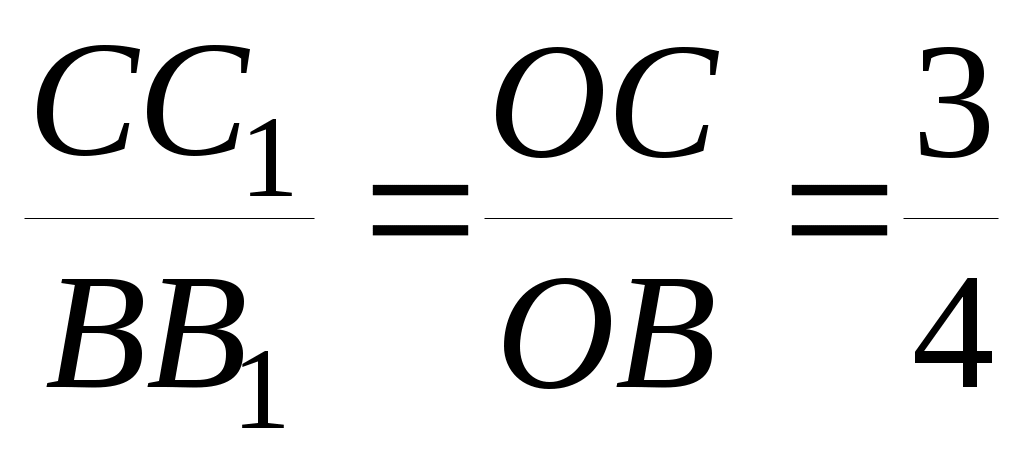 , но ВВ1=
, но ВВ1=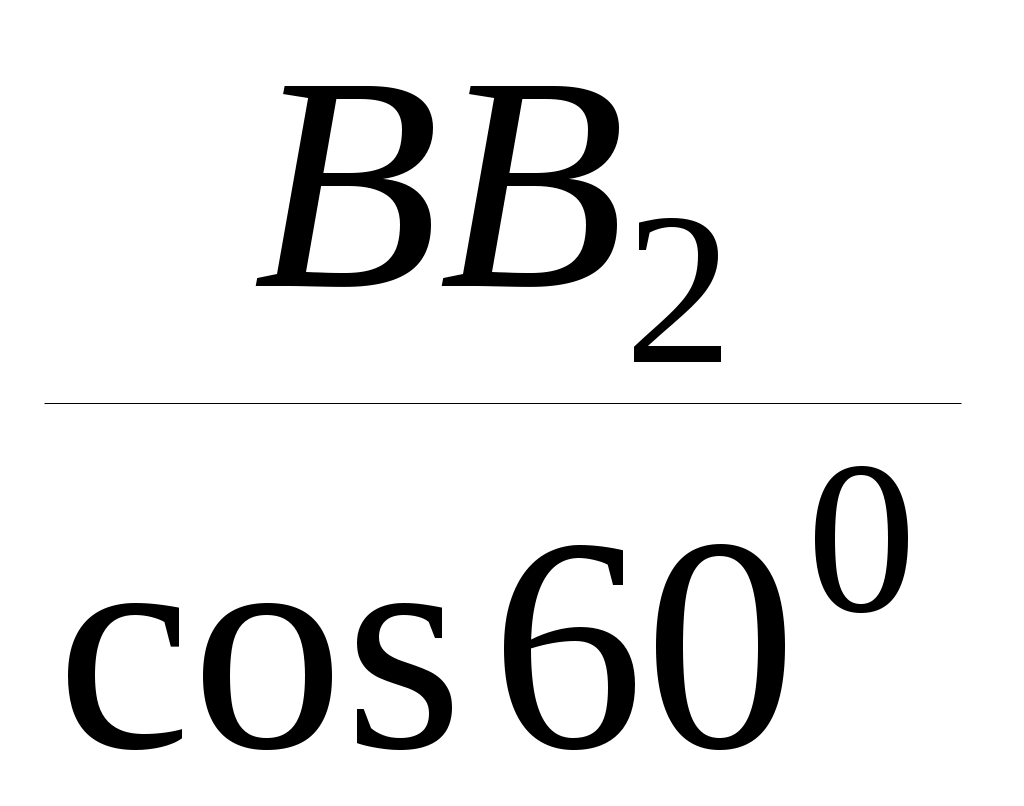 =
=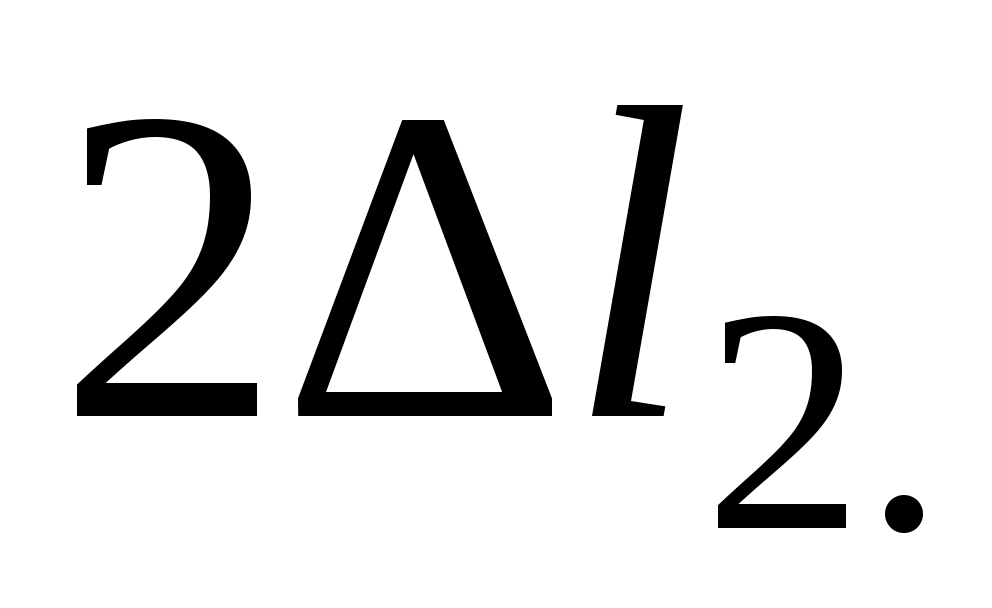
Таким образом,
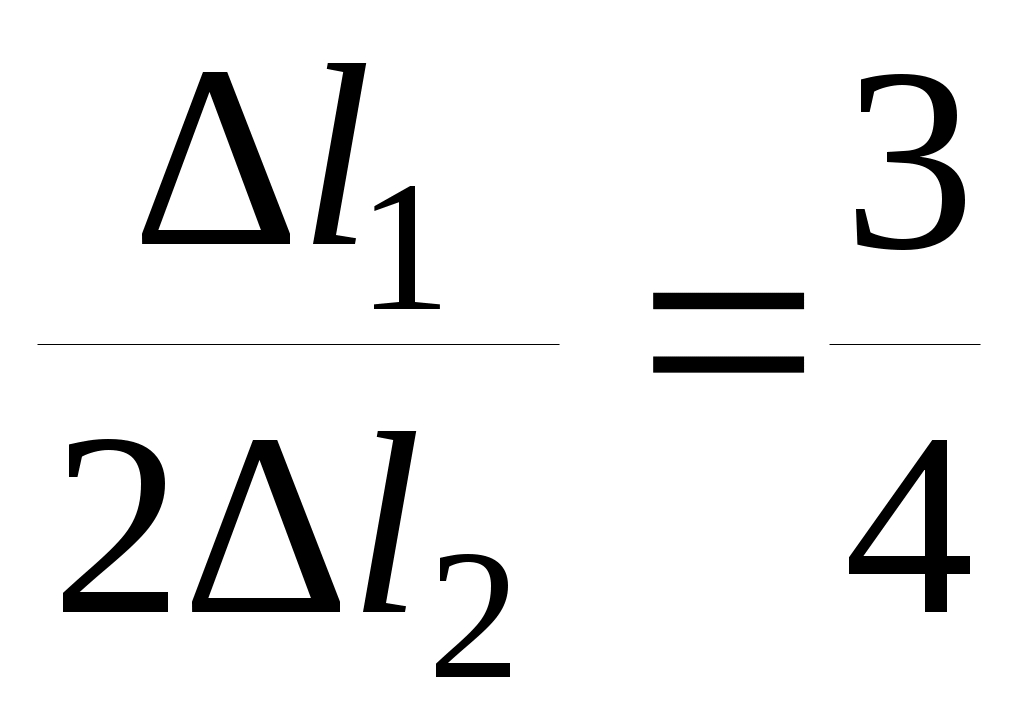 или
или 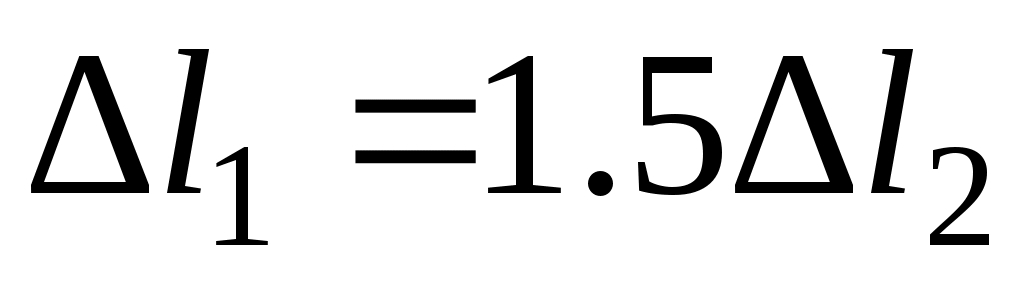 (2)
(2)
1.3.Физическая сторона задачи
В уравнении совместности деформации (2) подставим деформации, выраженные через усилия по закону Гука:
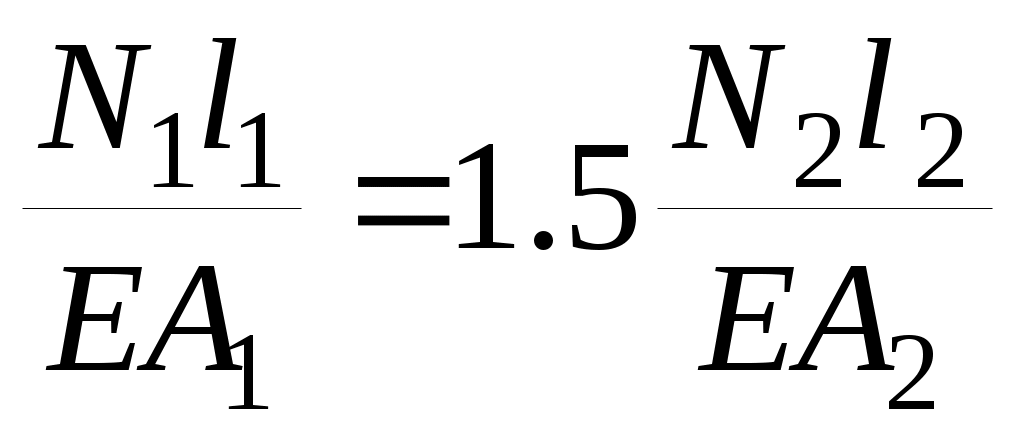 .
.
Подставим значения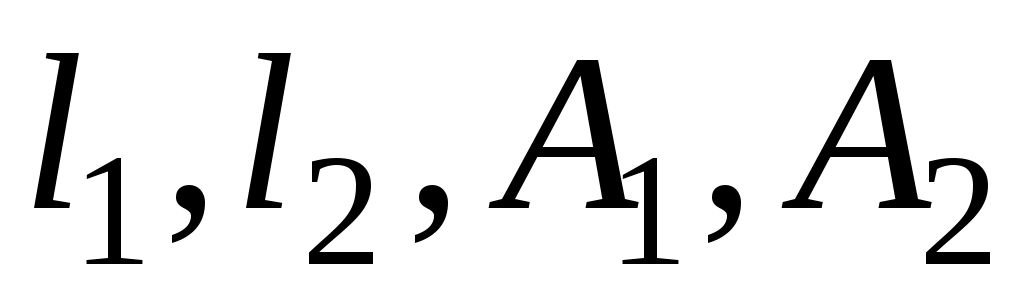 ,получим
,получим
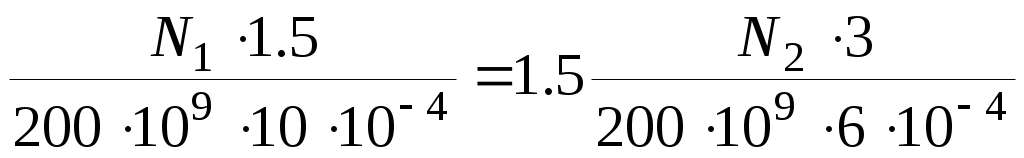 .
.
Окончательно N1=5N2. (3)
1.4.Синтез.
Решая совместно уравнения (1) и (3), находим усилия в стержнях 1, 2:
3N1+2N2=2F
N1=5N2,
откуда
N1=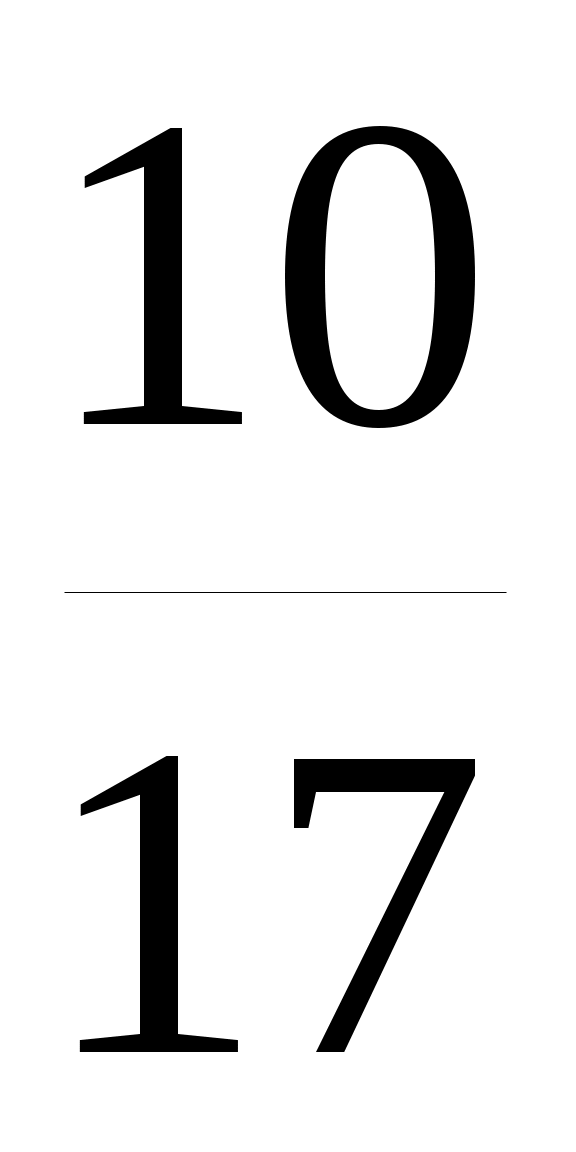 F; N2=
F; N2=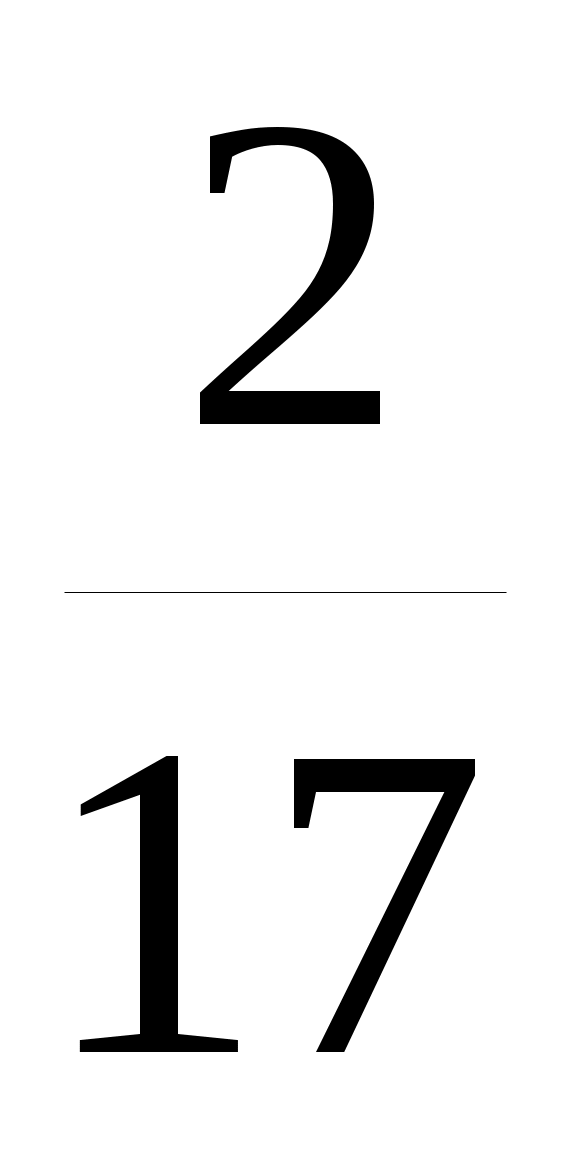 F
F
.
1.5.Нормальные напряжения в стержнях
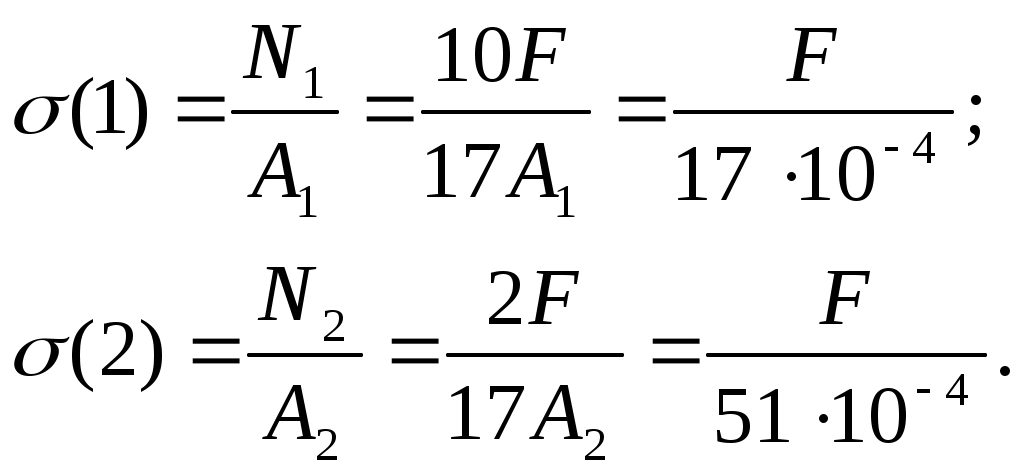
Сравнивая напряжения в стержнях 1 и 2, видим, что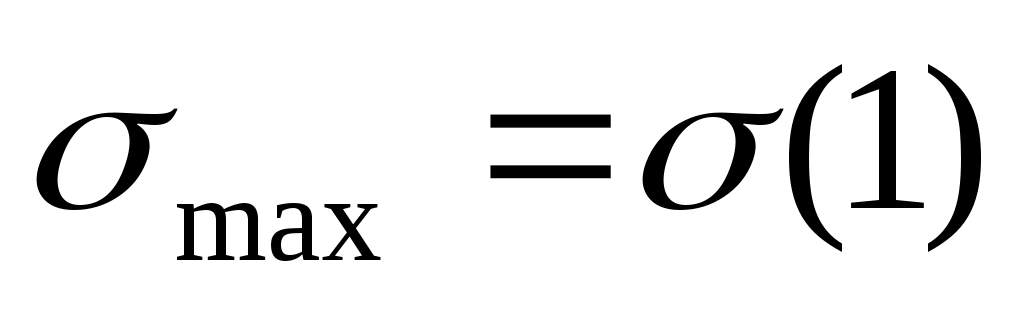 .
.
1.6. Допускаемая сила [F]
Записываем условие прочности
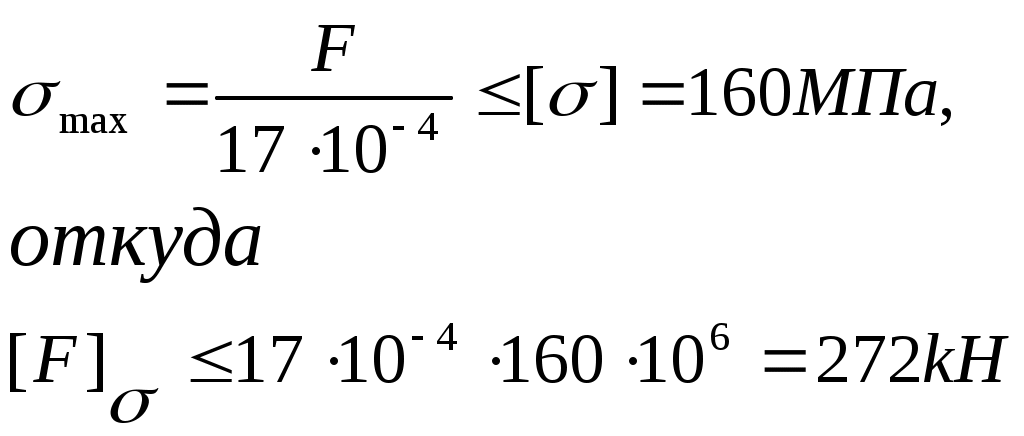
(из расчета по[ ]).
]).
2.Определение разрушающей нагрузки
Покажем систему в момент полного исчерпания несущей способности (см. рис. 4). Для полного исчерпания несущей способности системы необходимо, чтобы напряжения в стержнях 1,2 достигли предела текучести. При этом деформации в стержнях 1,2 будут, а брус ОБ начнет поворачиваться вокруг точки О при постоянной нагрузке.
Выражение для Fразр получим из условия равновесия в момент исчерпания несущей способности
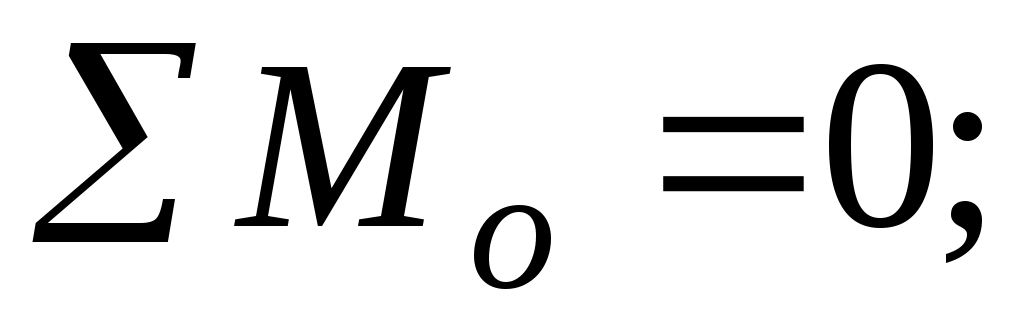
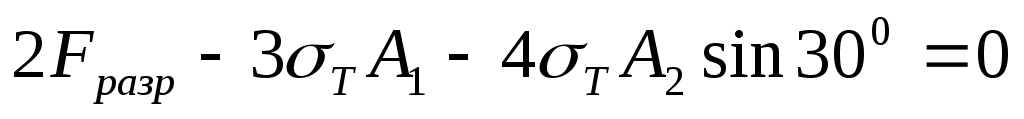 ,
,
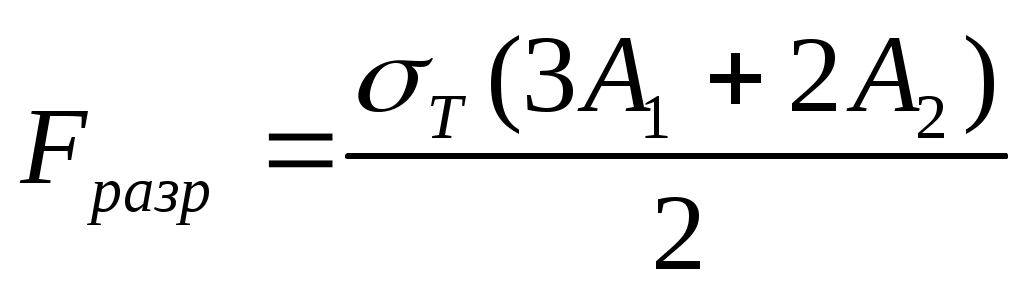 .
.
2.1.Допускаемая нагрузка
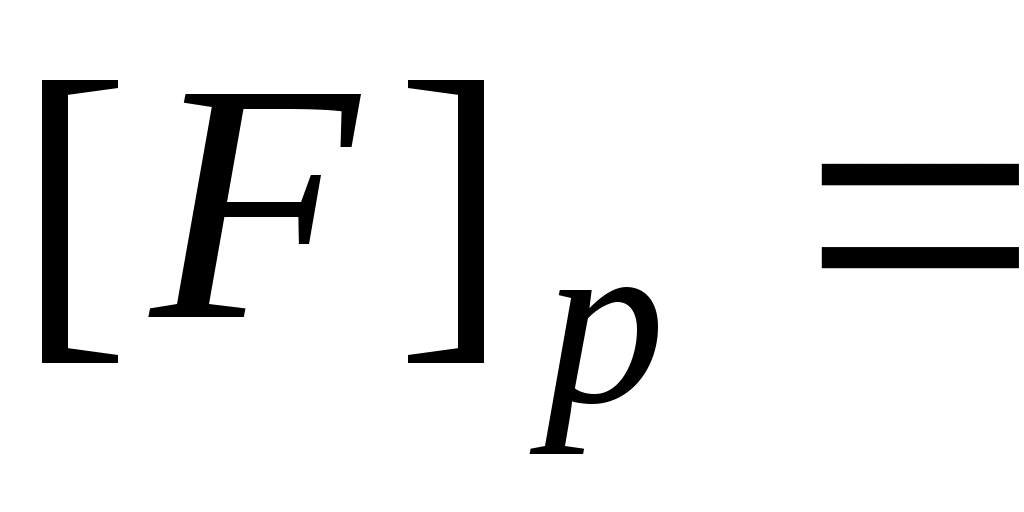
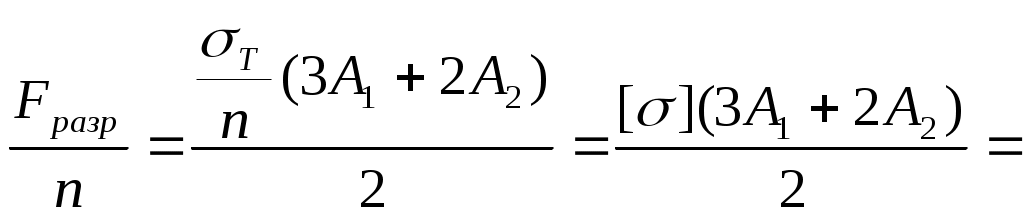

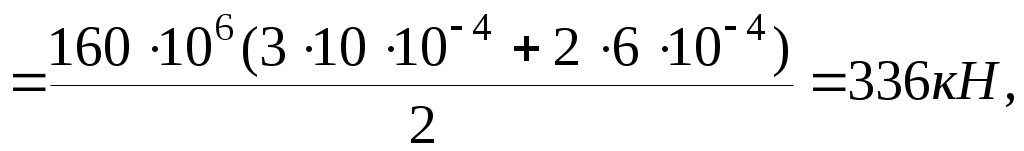
где n – коэффициент запаса прочности.
2.2. Грузоподъемность системы
Грузоподъемность системы при расчете по разрушающей нагрузке повысилась в
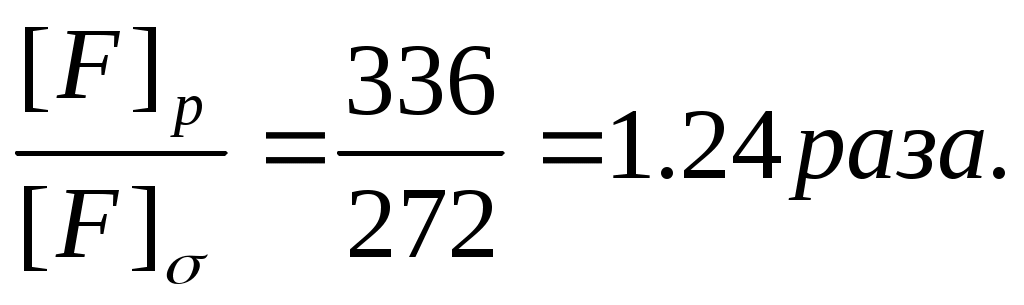
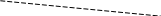
.
Проследим за характером работы системы в процессе постепенного возрастания силы F. Пусть зависимость () описывается диаграммой Прандтля (рис. 8) для идеального упруго-пластичного материала.
 Помним, что усилия в среднем стержне больше, чем в крайних, следовательно, в нем большими оказываются и напряжения. До тех пор, пока напряжения в среднем стержне не достигли предела текучести, усилия во всех стержнях изменяются пропорционально силе Fи определяются формулой ( 9.15). Как только в среднем стержне напряжения достигнут предела текучести, дальнейший рост силы Fне будет сопровождаться увеличением напряжений в среднем стержне; расти будут лишь напряжения в крайних стержнях, не достигших ещё предела текучести.
Помним, что усилия в среднем стержне больше, чем в крайних, следовательно, в нем большими оказываются и напряжения. До тех пор, пока напряжения в среднем стержне не достигли предела текучести, усилия во всех стержнях изменяются пропорционально силе Fи определяются формулой ( 9.15). Как только в среднем стержне напряжения достигнут предела текучести, дальнейший рост силы Fне будет сопровождаться увеличением напряжений в среднем стержне; расти будут лишь напряжения в крайних стержнях, не достигших ещё предела текучести.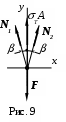 Возникновение напряжений в среднем стержне, равных пределу текучести, не означает, что узел О может перемещаться без возрастания силы F, так как опусканию узла О препятствуют крайние стержни, в которых напряжения ещё не достигли предела текучести. Таким образом, пластическая деформация среднего стержня задерживается крайними. Поэтому возникновение в среднем стержне напряжений, равных пределу текучести, ещё не является опасным для системы. Система ещё способна продолжать сопротивляться возрастающей нагрузке.
Возникновение напряжений в среднем стержне, равных пределу текучести, не означает, что узел О может перемещаться без возрастания силы F, так как опусканию узла О препятствуют крайние стержни, в которых напряжения ещё не достигли предела текучести. Таким образом, пластическая деформация среднего стержня задерживается крайними. Поэтому возникновение в среднем стержне напряжений, равных пределу текучести, ещё не является опасным для системы. Система ещё способна продолжать сопротивляться возрастающей нагрузке.Начиная с момента, когда в среднем стержне возникают напряжения Т, система перестает быть статически неопределимой, так как усилие в среднем стержне приобретает определенное значение Т А и не меняется при дальнейшем увеличении силы F. Усилия в крайних стержнях определяются из уравнений равновесия (рис. 9)
X=0; -N1sin + N2sin =0;
Y=0; N1cos +ТА + N2cos -F=0. (9.16)
Из первого уравнения N1= N2 ,
Тогда из второго 2N1cos +ТА - F=0
(9.17)
Нагрузка, при которой возникают напряжения Т в среднем стержне может быть обозначена FТ ; её находим из условия
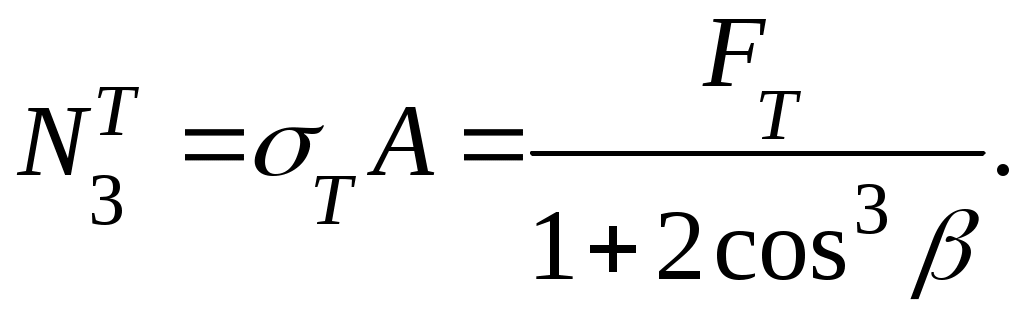
Дальнейший рост нагрузки приводит к тому, что и в крайних стержнях напряжения достигают предела текучести. При соответствующем значении нагрузки, которое обозначим Fоп , происходить опускание узла О без дальнейшего увеличения её. То есть система (все её элементы) будет испытывать возрастающие пластические деформации при постоянной нагрузке. Сила Fоп, которой соответствует возникновение опасного состояния системы, может быть найдено из равенства (9.17), если в нем положить N1 = Т А, т.е.
Отсюда
Нагрузка FТ , при которой впервые в системе возникают напряжения ( в среднем стержне), равные Т , меньше нагрузки Fоп , соответствующей возникновению опасного состояния системы:
Расчет по допускаемому напряжению сводится к условию прочности:
откуда
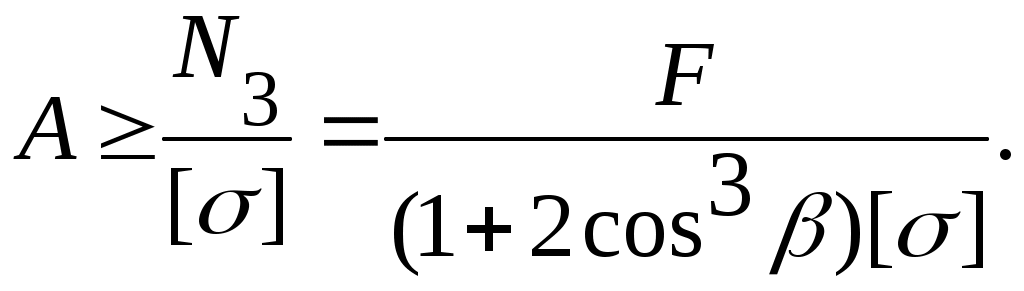 (9.18)
(9.18)При расчете по допускаемой нагрузке ставим условие, чтобы фактическая нагрузка F не была больше так называемой допускаемой:
Величину допускаемой нагрузки находим по формуле
Если принять коэффициент запаса прочности n таким же, как при определении [], получим
Условие прочности по допускаемой нагрузке в данном случае имеет вид
Площадь поперечного сечения стержней по допускаемой нагрузке
(9.20)
Сопоставляя формулы (9.18) и (9.20), легко обнаруживаем большую экономичность расчета по допускаемым нагрузкам при сравнении его с расчетом по допускаемым напряжениям.
Действительно, если положить, например, что =300 (cos= 3 2), то по допускаемому напряжению будем иметь
Производя аналогичную операцию по допускаемой нагрузке, получим
Перерасход материала при расчете по допускаемому напряжению составил 19% по сравнению с расчетом по допускаемой нагрузке.
9.1.4. Пример выполнения домашнего задания
Содержание задания:
Абсолютно жестким брус ОВ поддерживается с помощью стальных стержней 1, 2. Площади поперечных сечений: А1=10 см2, А2=6см2. Допускаемое напряжение материала стержней [
Начертим заданную схему в масштабе и проставим размеры в системе СИ (см. рис. 1).
Решение
1. Определение допускаемой силы
Освободимся от связей, наложенных на брус ОВ (см. рис. 2). Для полученной плоской системы сил можно составить три независимых уравнения равновесия статики
Неизвестных усилий – четыре. Таким образом, степень статической неопределимости
n=4нз-3ур=1раз.. статически неопределимая задача.
Для записи условия прочности нам необходимо знать усилия в стержнях 1,2 и совсем не обязательно знать реакции в опоре.
Дальнейшее решение задачи по плану для СНЗ.
1.1. Статическая сторона задачи (см. рис. 2).
N1 3+ N2sin300=0,
откуда 3N1+2N2=2F. (1)
1.2. Геометрическая сторона задачи
Для составления уравнения совместности деформации покажем систему в деформированном состоянии (см. рис. 3). В результате деформации стержней 1,2 брус ОВ повернется вокруг опоры О, точки В и С перейдут в положение В1 и С1 (см. рис. 3). Как видно из рис.3,
Соотношение между деформациями стержней получим из подобия треугольников
Таким образом,
1.3.Физическая сторона задачи
В уравнении совместности деформации (2) подставим деформации, выраженные через усилия по закону Гука:
Подставим значения
Окончательно N1=5N2. (3)
1.4.Синтез.
Решая совместно уравнения (1) и (3), находим усилия в стержнях 1, 2:
3N1+2N2=2F
N1=5N2,
откуда
N1=
.
1.5.Нормальные напряжения в стержнях
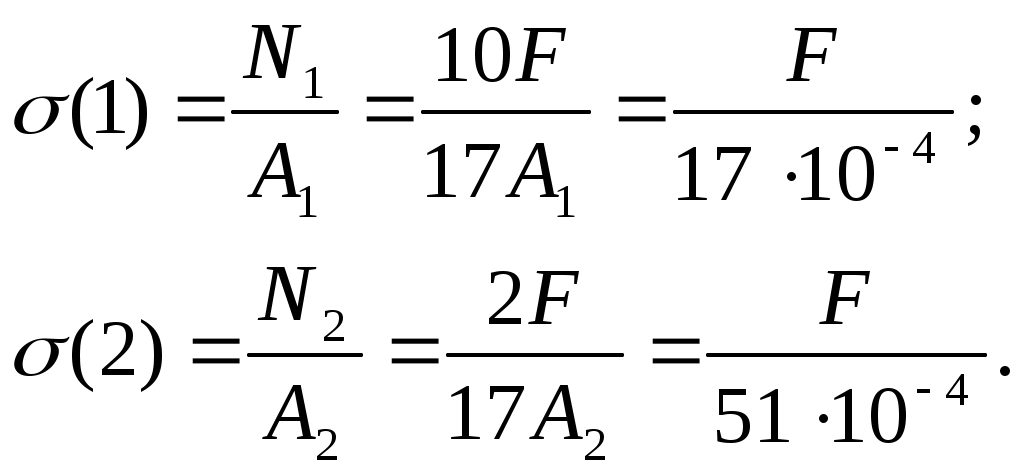
Сравнивая напряжения в стержнях 1 и 2, видим, что
1.6. Допускаемая сила [F]
Записываем условие прочности
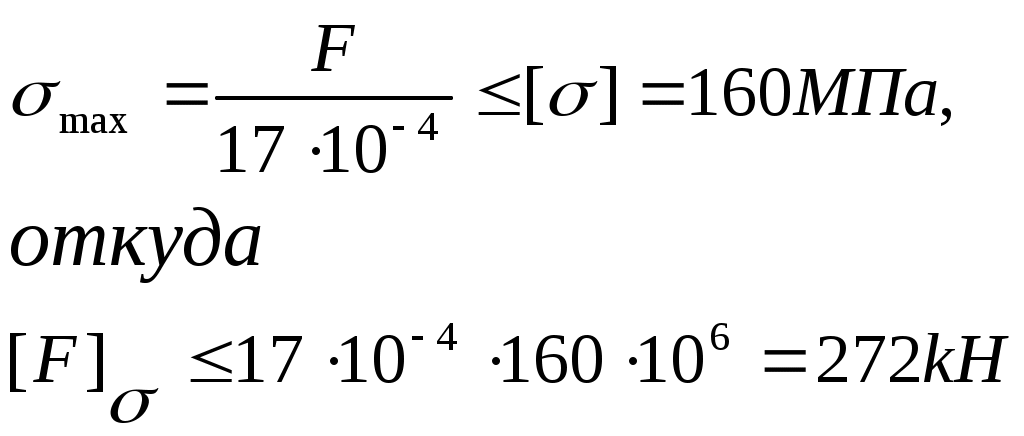
(из расчета по[
2.Определение разрушающей нагрузки
Покажем систему в момент полного исчерпания несущей способности (см. рис. 4). Для полного исчерпания несущей способности системы необходимо, чтобы напряжения в стержнях 1,2 достигли предела текучести. При этом деформации в стержнях 1,2 будут, а брус ОБ начнет поворачиваться вокруг точки О при постоянной нагрузке.
Выражение для Fразр получим из условия равновесия в момент исчерпания несущей способности
2.1.Допускаемая нагрузка
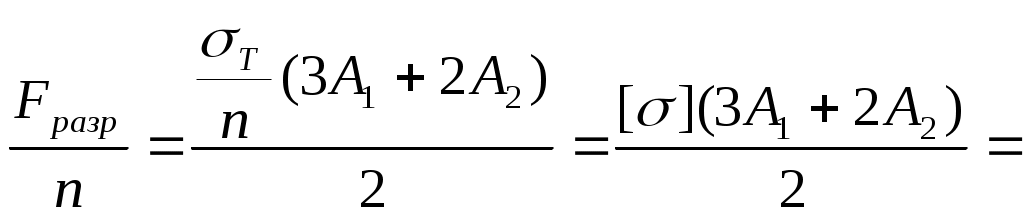
где n – коэффициент запаса прочности.
2.2. Грузоподъемность системы
Грузоподъемность системы при расчете по разрушающей нагрузке повысилась в

.