Файл: Курс лекций по сопротивлению материалов Уфимский государственный нефтяной технический университет, 2012 Введение Задачи, цель и предмет курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 403
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу
Для расчёта на прочность таких конструкций пользуются расчётной моделью в виде оболочки.
Отсюда определяется меридиональное напряжение т.
Напряженное состояние является двухосным
где G -вес жидкости в объёме расположенным ниже отсеченной части оболочки
9.2. Статически неопределимые стержневые конструкции,
работающие на кручение
9.2.1. Раскрытие статической неопределимости при кручении
П р и м е р 1. Стальной стержень (рис. 9.9), имеющий на одной половине сплошное сечение, а на другой - полое, нагружен крутящим моментом
М=40 кНм. Определить наибольшие касательные напряжения на левой и правой частях стержня и угол поворота среднего сечения.
Решение. Составим единственно возможное уравнение равновесия
которое содержит два неизвестных реактивных момента. Следовательно, система однажды статически неопределима.
Составим дополнительное уравнение деформаций из условия, что
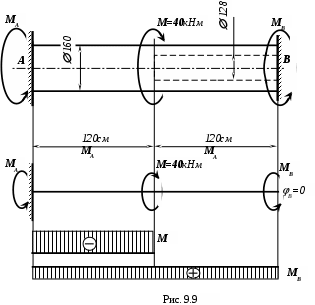
Отбросим заделку В и заменим её действие на стержень моментом МВ.
Тогда, применяя принцип независимости действия сил, получим уравнение деформаций
где
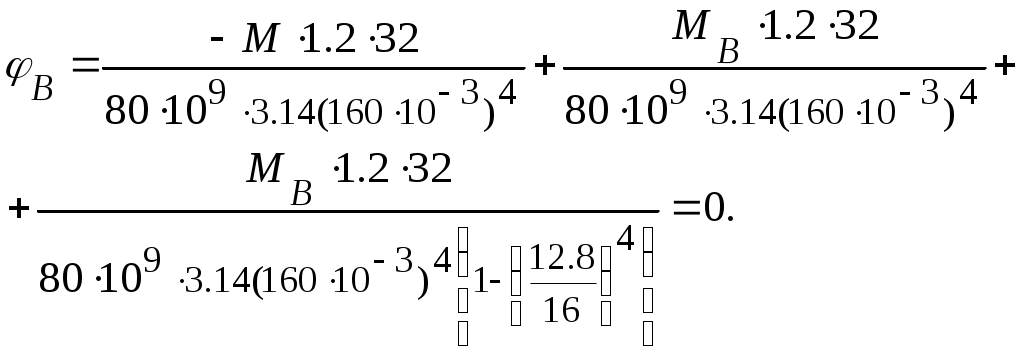
Откуда, МВ = 15кНм.
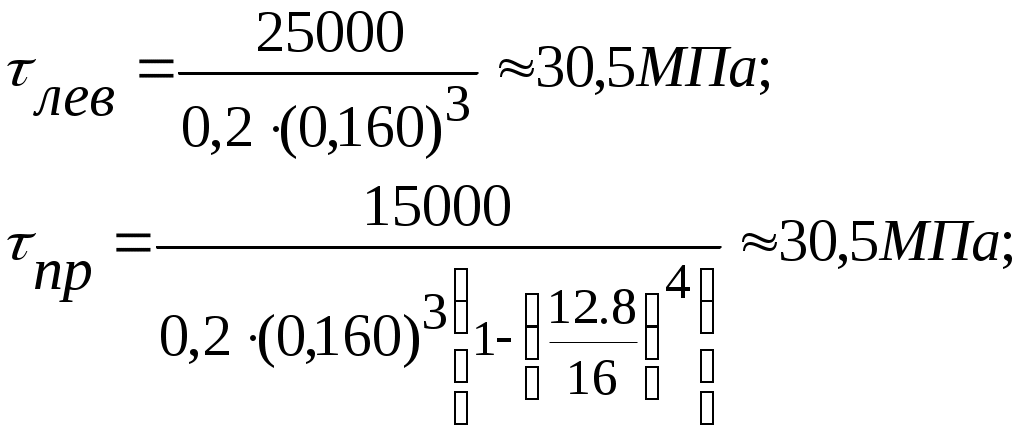
9.2.2. Понятие о кручении круглого стержня за пределами упругости
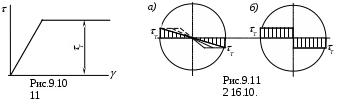
Рассмотрим случай кручения круглого стержня в процессе непрерывного нарастания крутящего момента. Для упрощения решения примем диаграмму Прандтля изменения касательных напряжений в зависимости от угла сдвига
g, на которой площадка текучести распространяется безгранично (рис. 9.10).
Такое допущение является условным, так как при этом не учитывается зона упрочнения, а также то, что в наиболее удаленных волокнах стержня может наступить разрушение материала при сдвиге. Поэтому приводимое ниже решение является приближенным.
Когда наибольшее касательное напряжение в точках на контуре сечения достигнет предела текучести tТ , крутящий момент можно определить по обычной формуле
М1 =WP tТ . (9.21)
Эпюра касательных напряжений для этого случая показана на рис. 9.11,а. При дальнейшем увеличении крутящего момента на контуре сечения образуется кольцеобразная пластическая зона, постепенно проникающая внутрь сечения. Эпюра напряжений видоизменяется и на рис. 9.11,а показана пунктиром. Условно считаем, что пластическая зона распространяется до центра сечения. Тогда эпюра касательных напряжений имеет вид, показанный на рис. 9.11,б.
Предельный разрушающий момент определяется так (см. рис. 9.12).
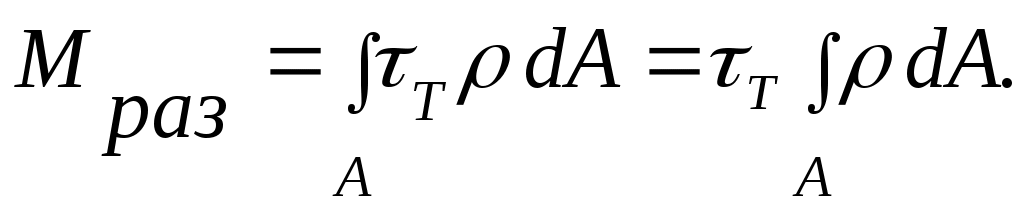
Согласно рис. 13 имеем
следовательно,
Обозначим выражение
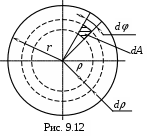 Поэтому
ПоэтомуСравнивая выражения (9.21) и (9.22), видим, что предельный разрушающий момент больше момента МZ, который вызывает текучесть только в точках на контуре сечения. Отношение этих моментов
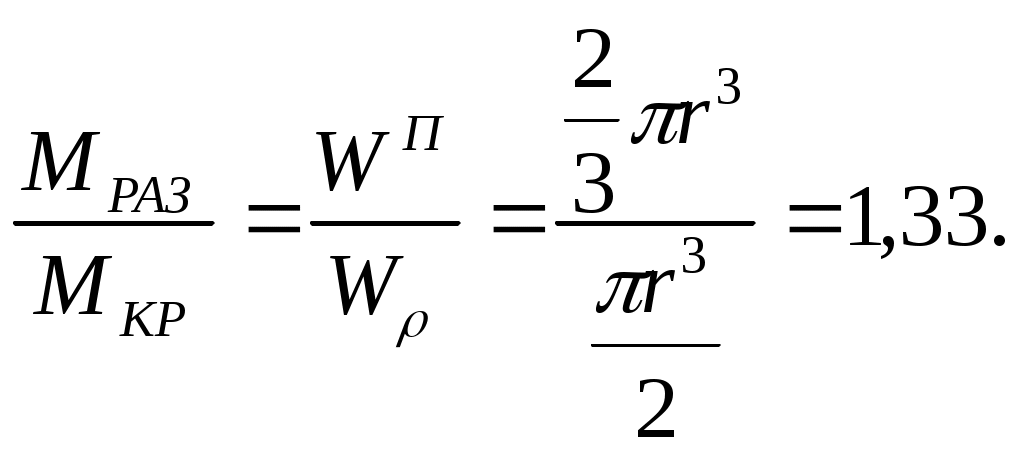
Если предположить, что коэффициент запаса для двух случаев один и тот же, то момент, который можно приложить к стержню при расчете по разрушающему моменту, будет больше на 33% допускаемого момента, найденного по допускаемым напряжения.
П р и м е р 2. Рассмотрим стальной стержень (рис. 9.9), для исчерпания несущей способности этого стержня необходимо, чтобы поперечные сечения в заделках находились бы в состоянии текучести.
Тогда
где -
Следовательно,
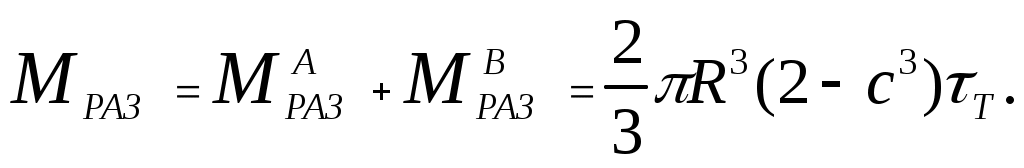 (9.23)
(9.23)Сравнивая выражения (9.21) и (9.23) получим:
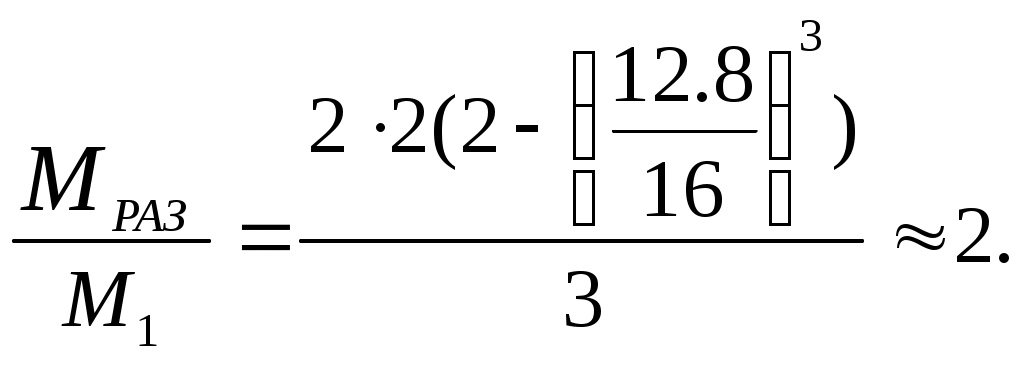
9.3. Статически неопределимые балки при изгибе
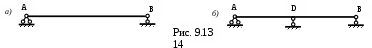
Для определения внутренних усилий, напряжений и деформаций нами систематически применялось одно и то же аналитическое средство - уравнения равновесия. С помощью этих уравнений, записанных для стержня в целом, мы сначала находим опорные реакции, а затем, используя метод сечений (РОЗУ) - определяем внутренние силы. И пока этот метод себя оправдал, но в ряде случаев для определения опорных реакций и внутренних усилий этих уравнений попросту недостаточно. Очень часто по условию работы в кинематически неподвижной балке (рис. 9.13, а) необходимо увеличить число опор (рис. 9.13, б). Опора D-не «лишняя», т.к. при её отсутствии прочность и жёсткость балки может оказаться необеспеченной.
Если уравнений статики недостаточно для определения опорных реакций и внутренних усилий в стержневой системе, то получаем статически неопределимую задачу.
Поэтому возникает необходимость составлять некие дополнительные уравнения, которые формируются вне связи с уравнениями равновесия. Обычно это уравнения условиясогласованности или совместности деформаций.
9.3.1. Степень статической неопределимости
То число связей, при котором достигается кинематическая неизменяемость, носит название необходимое число связей.
Всякую связь, наложенную сверх необходимых, называют дополнительной.
Число дополнительных связей определяет степень статической неопределимости системы.
Связи делятся на внешние и внутренние.
Внешние связи накладывают условия на абсолютное перемещение некоторых точек системы.
П

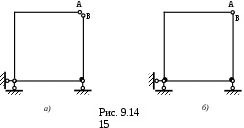
од внутренними связями понимают ограничение, накладываемое на взаимное смещение элементов системы (рамы). Рассмотрим примеры на рамной системе.
На (рис. 9.14,а) рама имеет три необходимые внешние связи. Задача статически определима.
На (рис. 9.14,б) рама имеет три необходимые внешние связи и две внутренние дополнительные связи, запрещающие взаимное вертикальное и горизонтальное смещение точек А и В. Задача дважды статически неопределима и для решения задачи требуется два дополнительных уравнения.
9.3.2. Метод сил
9.3.2.1. Выбор основной системы
Наиболее общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так внутренних, а их действие заменяется неизвестными силами и моментами. Так образуется статически определимая система с заданными и неизвестными силами, которая кинематически должна соответствовать заданной системе. Такая система называется основной.
При указанном способе решения задачи неизвестными оказываются силы – отсюда название «метод сил».
Для каждой статически неопределимой стержневой или рамной системы можно подобрать, как правило, сколько угодно основных систем, они должны быть статически определимыми и геометрически неизменяемы. При подборе основных систем нельзя формально руководствоваться только одним правилом, что число отбрасываемых связей должно быть равно степени статической неопределимости, этого недостаточно, необходимо следить и за тем, какие связи отбрасываются, чтобы не нарушить кинематическое соответствие с заданной системой (т.е. следить за перемещениями).
Пример. Для одной балки представлены разные основные системы(рис. 9.15, а, б), при этом уравнения деформации будут иметь различный геометрический смысл.
Для а) уравнение деформации vA=0;
б) уравнение деформации jВ=0.
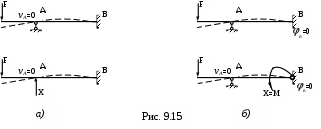
Неизвестная сила Х отрицает перемещение сечения в т. А, а неизвестный момент Х=М отрицает угол поворота сечения в заделке.
9.3.2.2. Порядок расчета простейших статически неопределимых балок
Рассмотрим порядок расчета простейших статически неопределимых балок на следующем примере.
П р и м е р 1. На рисунке 9.16, а) показана один раз статически неопределимая балка. Один из возможных вариантов основной системы (см. рис. 9.16, б, 9.16, в). Рассмотрим основную систему (см. рис. 9.16, б), когда правая шарнирно- подвижная опора заменяется неизвестным усилием X1.
Условием деформации основной системы является требование исключить вертикальное перемещение (прогиб) в точке В.
Выражение для прогиба vBможет быть представлено в виде
vB = vBХ1+vBq=0, (9.24)
где vBХ1 – прогиб балки в точке В основной системы, вызванный неизвестной силой Х1;
vBq- прогиб балки в точке В основной системы, вызванный только равномерно распределённой нагрузкой q.
Из уравнения (9.24) видно, что прогиб конца консоли от совместного действия нагрузки qи силы Х1 равен нулю. Деформации балки, вызванные отдельно нагрузкой q и неизвестной силой Х1, изображены на рис. 9.16, д.
Для определения прогибов точки В (или 1) можно воспользоваться любым известным методом или способом.
При решении задачи воспользуемся: способом Верещагина и методом начальных параметров.
По способу Верещагина (рис. 9.16, е)
По методу начальных параметров (рис. 9.16, ж)
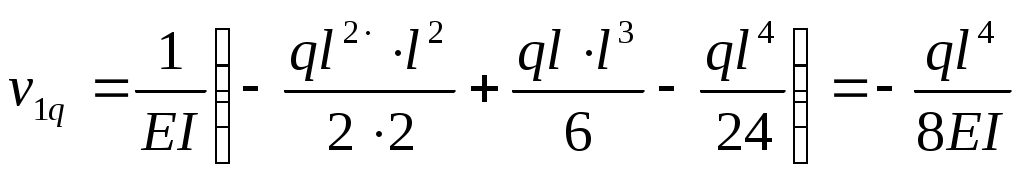 .
.Подставляя найденные значения прогибов в уравнение (9.24), получим
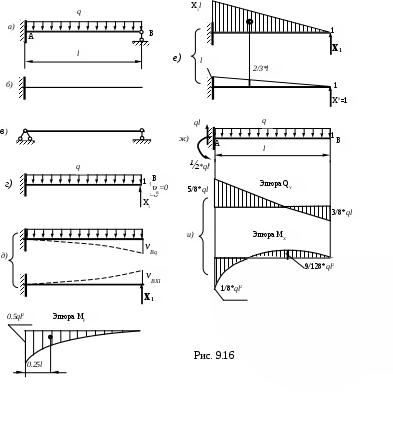
После определения «лишней» неизвестной Х1 строятся окончательные эпюры поперечных сил и изгибающих моментов обычными методами, как для статически определимых балок (рис. 9.16, и).
В дальнейшем при составлении уравнений совместности деформации типа (9.24) запись этих уравнений целесообразно вести с помощью обозначения перемещений, имеющих стандартную (каноническую) форму.
9.3.2.3. Канонические уравнения метода сил
Запишем уравнение (9.24) так:
D1=D1Х1+D1F =0, (9.25)
где D1Х1 - перемещение точки В (т.1) в направлении действия Х1, вызванное неизвестным усилием Х1;
D1F - перемещение точки В (т.1) в направлении действия неизвестного Х1, вызванного нагрузкой F. У нас под индексом (F ) подразумевается нагрузка q.
Перемещение от неизвестного Х1 удобно представить в виде
D1Х1=d11× Х1,
где d11 – перемещение точки В (т.1) основной системы в направлении действия Х1, вызванное единичным воздействием
Таким образом, уравнение (9.25) принимает вид
d11× Х1+D1F= 0. (9.26)
Коэффициенты d11 и D1F определяются по формулам:
где
МF - эпюра (или функция) моментов в основной системе от приложенных к балке сил F( у нас подразумевается нагрузкаq);
EI - жёсткость балки при изгибе.
Индекс “s”, стоящий внизу интеграла, означает, что интегрирование распространяется на все элементы системы.
Н
айдём коэффициенты уравнения (9.26), воспользовавшись правилом перемножения эпюр по Верещагину:
Здесь в круглых скобках выполнен подсчёт площадей. В квадратные скобки выделены ординаты под центром тяжести указанной площади, взятые из линейной эпюры (см рис.9.16,ж).
После подстановки значений d11иD1F в уравнение (9.26) получим
Х1=(3/8)ql.
Далее строим эпюры Qу и Mх. (рис. 9.16,и).
В строительной практике часто встречаются статически неопределимые балки, имеющие несколько промежуточных опор. Такие балки называются неразрезными. Весьмасущественное значение при расчёте таких балок имеет рациональный выбор основной системы.
На рис. 9.17 показана четыре раза статически неопределимая неразрезная балка и два возможных варианта основной системы.
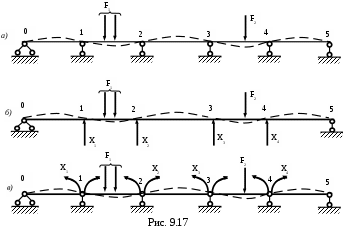
По первому варианту основной системы (рис. 9.17,б) за неизвестные величины приняты величины опорных реакций Х1… Х4 .Смысл канонических уравнений в этом случае состоит в отрицании перемещений точек 1, 2, 3, 4 оси балки по вертикали. Во втором варианте основной системы (рис. 9.17, в) неразрезная балка превращается в пять простых двухопорных балок постановкой полных шарниров под промежуточными опорами. В этом случае лишними неизвестными являются изгибающие моменты в сечениях над промежуточными опорами, и они будут определяться из условия неразрывности балки над опорами. Смысл канонических уравнений в этом случае состоит в отрицании углов раскрытия двух бесконечно близких сечений балки, взятых над промежуточными опорами.
В обоих рассматриваемых вариантах решения получим систему совместных
d11C1+d12C2+d13C3+d14C4+D1F=0;
d21C1+d22C2+d23C3+d24C4+D2F=0; (9.27)
d31C1+d32C2+d33C3+d34C4+D3F=0;
d41C1+d42C2+d43C3+d44C4+D4F=0.
Следует отметить, что по первому варианту каждое из уравнений системы содержит все nнеизвестных.
Во втором варианте каждое из уравнений системы содержит независимо от степени статической неопределимости системы не более трех неизвестных, так как деформация, возникающая от любого из неизвестных, распространяется только в пределах двух прилегающих пролетов.
Поэтому второй вариант значительно проще, особенно для системы с большим числом неизвестных.
П р и м е р 2. Раскрыть статическую неопределимость заданной балки (рис. 9.18,а) и построить эпюры поперечных сил и изгибающих моментов.
Р е ш е н и е. Заданная система имеет две “лишних” связи. Следовательно, балка дважды статически неопределима и система канонических уравнений метода сил (КУМС) примет следующий вид:
d11C1+d12C2+D1F=0;
d21C1+d22C2+D2F=0.
За неизвестные примем изгибающие моменты: в заделке Х1 и в промежуточной опоре Х2, что равносильно врезке шарниров, т.е. получили один из возможных (рекомендуемый) вариантов основной системы (см. рис. 9.18,б).
Найдём коэффициенты уравнений, воспользовавшись правилом перемножения эпюр по Верещагину:
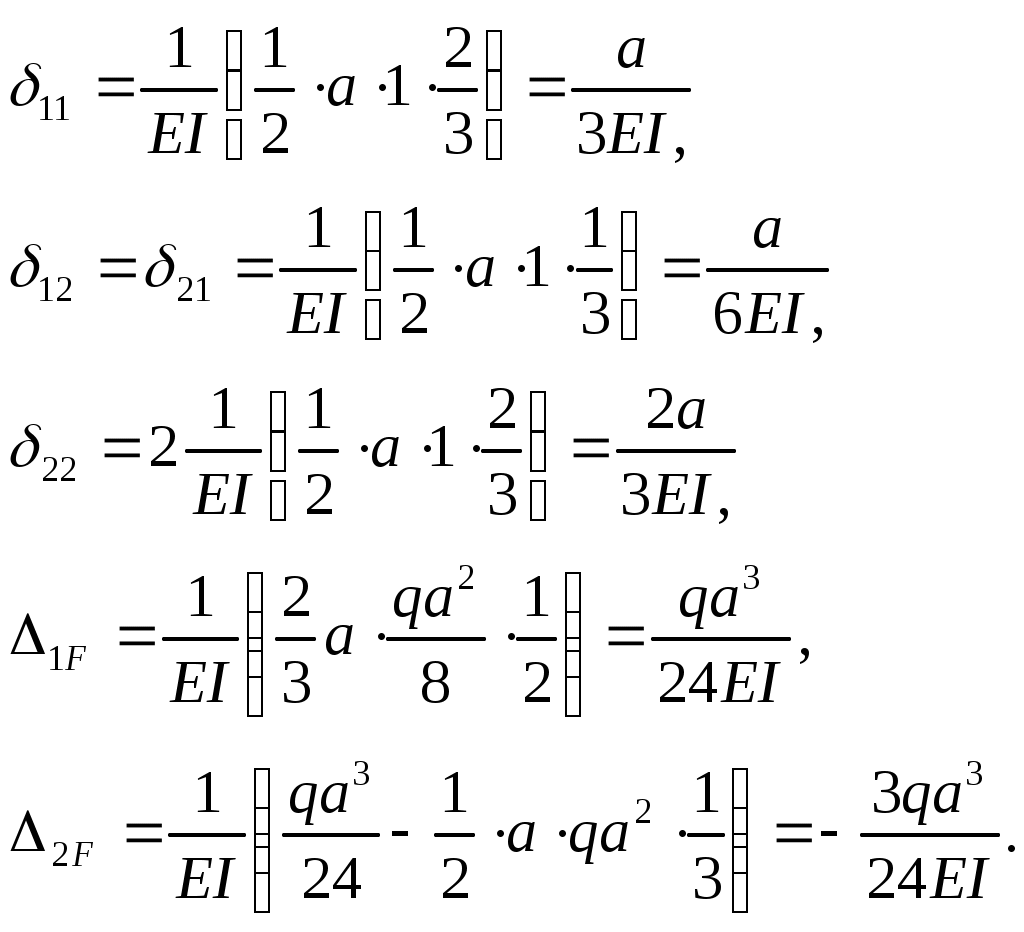
Подставим их в канонические уравнения и умножив на
Решая эту систему уравнений, получим значения ” лишних” неизвестных:
Знак минус указывает на то, что направление ” лишнего” изгибающего момента Х1 противоположно предварительно принятому.
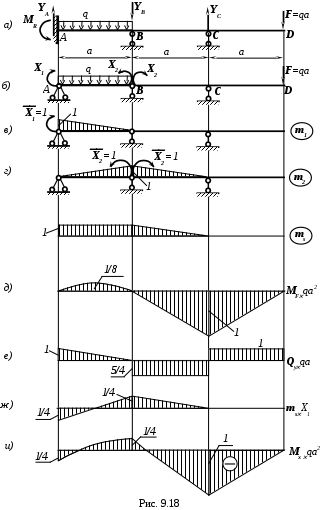
Определим опорные реакции, для этого мысленно рассечем балку и получим две. При этом к каждой полученной балке приложим вычисленный, согласно основной системе, ” лишний” изгибающий момент (рис. 9.19а,б).
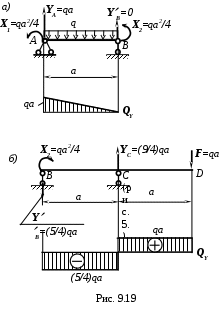 Рассмотрим балку АВ:
Рассмотрим балку АВ: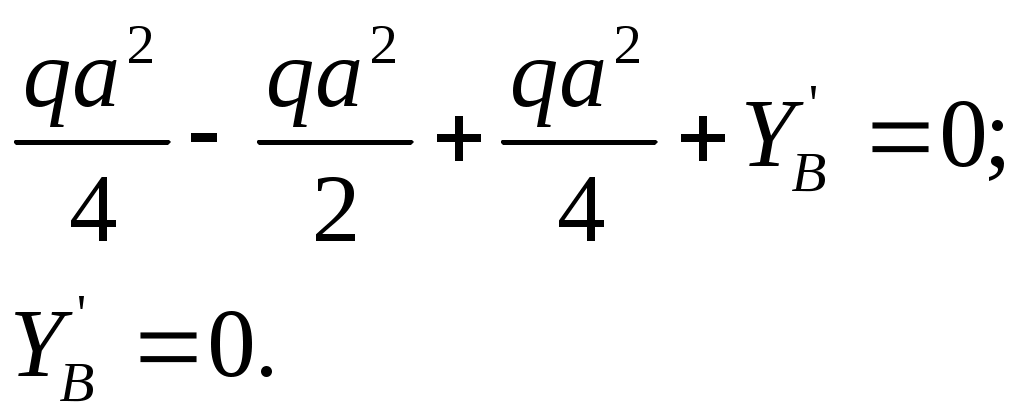
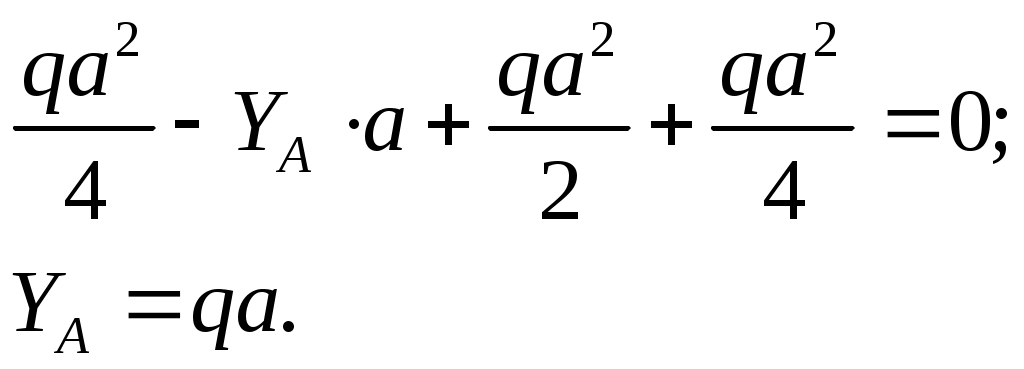
Рассмотрим балку ВD:
Состыкуем эпюры QY и по сумме реакций смежных пролетов, т.е. по “скачку”, определим полные реакции в каждой промежуточной опоре (рис. 9.18, е):
YA=qa; YB=(5/4)qa; YA=qa; YC=(9/4)qa.
Далее строим исправленную эпюру моментов (mS´X1) (рис. 9.18,ж).
Ординаты окончательной эпюры моментов для статически неопределимой балки вычисляются по формуле
МХ = МF+(mS´X1).
Окончательная эпюра моментов представлена на рис. 9.18,и.
-
9.3.3. Расчет статически неопределимых балок по методу
разрушающих нагрузок
9.3.3.1. Понятие об изгибе балок за пределами упругости
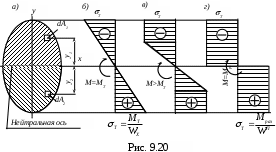
При расчете балок по наибольшим напряжениям, возникающим в наиболее удаленном волокне, за опасное состояние принимается такое, при котором в наиболее напряженном сечении максимальные напряжения для пластического материала достигают предела текучести (sТ) (см. рис. 9.20,б), для хрупкого материала – предела прочности (sВ).
Однако легко заметить, что такое состояние балки из пластического материала не является опасным, так как во всех остальных волокнах поперечного сечения напряжение меньше опасного и потому грузоподъёмность балки не исчерпана.
Дальнейшее увеличение нагрузки на балку будет вызывать текучесть по глубине в соседних волокнах и увеличение напряжений в соседних сечениях до предела текучести (см. рис. 9.20,в).
Грузоподъёмность сечения при изгибе будет полностью исчерпана лишь в том случае, если образуется ”пластический шарнир” т.е. напряжения по всему сечению будут равны (sТ) ( см. рис. 9.20,г).
 Для неразрезных балок образование одного ”пластического шарнира” не вызывает их разрушения, так как грузоподъёмность балки ещё полностью не исчерпана. Балка будет разрушена лишь тогда, когда в ней образуется несколько пластических шарниров, которые превращают балку в геометрически изменяемую систему.
Для неразрезных балок образование одного ”пластического шарнира” не вызывает их разрушения, так как грузоподъёмность балки ещё полностью не исчерпана. Балка будет разрушена лишь тогда, когда в ней образуется несколько пластических шарниров, которые превращают балку в геометрически изменяемую систему.Для расчета статически неопределимых балок по методу разрушающих нагрузок принимаем гипотезу об идеальной упруго-пластической работе материала (рис. 9.21).
Рассмотрим частный пример неразрезной балки с двумя пролётами одинаковой длины lпри действии одной сосредоточенной силы
F(рис. 9.22, а).
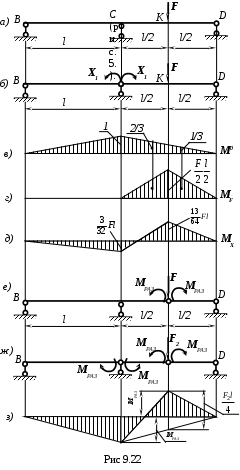
Основная система представлена на (рис. 9.22, б), где Х1 -”лишний” изгибающий момент
Каноническое уравнение запишем в виде
Получим величины единичных и грузовых перемещений:
Подставим их в каноническое уравнение и получим Х1:
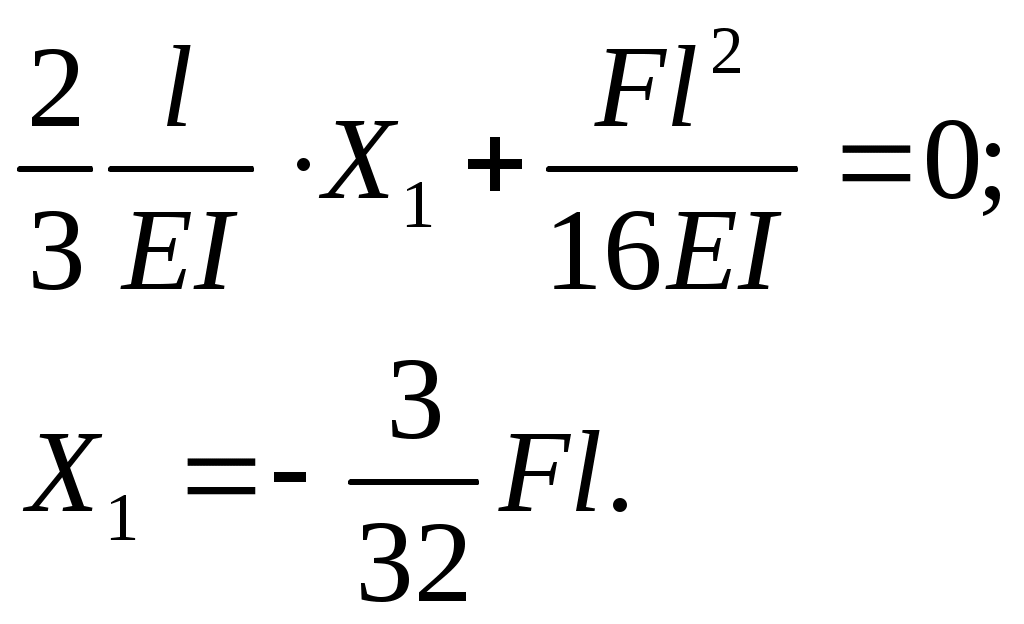
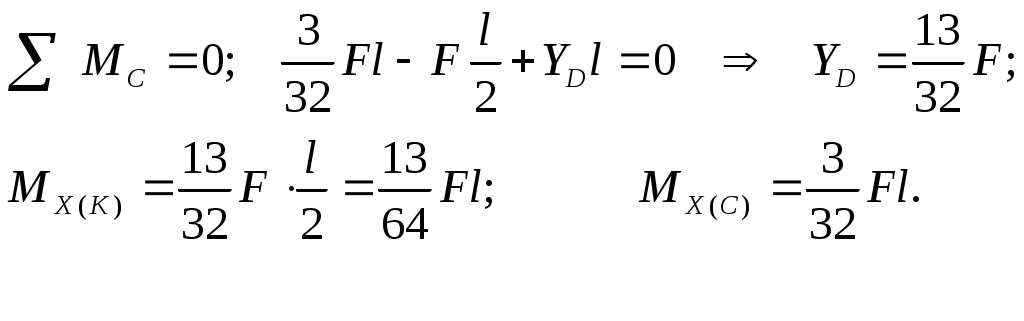
Эпюра моментов (МХ ) при упругой работе балки представлена на рис. 9.22, д).
При расчете по допускаемым напряжениям наибольшая нагрузка, которая может быть допущена из условия появления первой текучести (см. рис. 9.20,б) в наиболее напряженном месте ( под грузом), определится из выражения
откуда
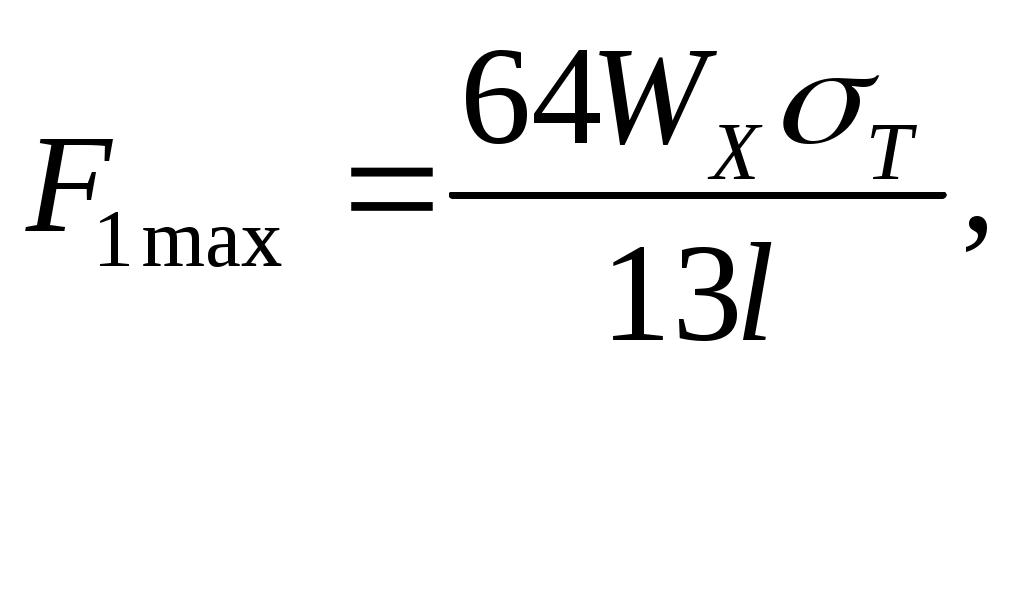 (9.28)
(9.28)где WX – момент сопротивления сечения относительно оси х.
Дальнейшее увеличение силы F приводит к распределению пластических зон вглубь сечения и появлению пластического шарнира в сечении К-К.
В этом случае балка превращается в статически определимую с промежуточным шарниром в сечении К-К, к которому приложены момент Мраз и груз (сила F).
Таким образом, появление пластического шарнира не приводит к разрушению балки, а всего лишь снижает степень её статической неопределимости на единицу.
При дальнейшем возрастании нагрузки будет увеличиваться момент над средней опорой и при F=F2max в этом сечении также образуется пластический шарнир (рис. 9.22,ж). С появлением второго пластического шарнира исчерпывается грузоподъемность балки, так как она превращается в геометрически изменяемую систему. Следовательно, разрушающая нагрузка должна быть подсчитана из условия появления двух пластических шарниров (рис. 9.22, ж). Эпюра моментов для этого случая показана на (рис. 9.22, и). Изгибающий момент в пластическом шарнире по абсолютной величине
где WП– пластический момент сопротивления сечения;
WП=2Smaxдля симметричного (относительно нейтральной оси) сечения;
здесь
Нейтральная ось х1делит площадь поперечного сечения балки на две равновеликие части.
Находим опорную реакцию
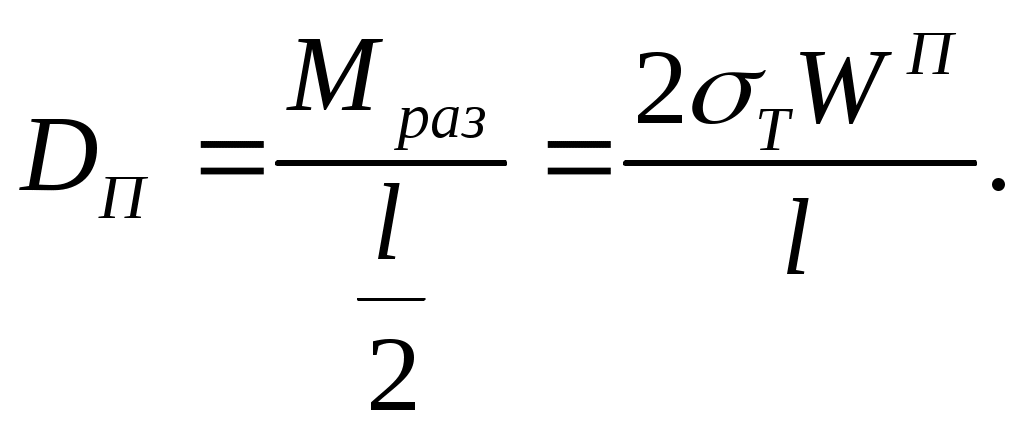
Уравнение равновесия относительно т.С для правой части балки имеет вид
Подставим сюда значение DП и решим относительно F2=F2max, тогда
разрушающая нагрузка определится из выражения
Так как W П > WX, то из сравнения (9.28) и (9.29) видно ,что F2max> F1max.
Найдем отношение F2max к F1max:
где
Для прямоугольного сечения
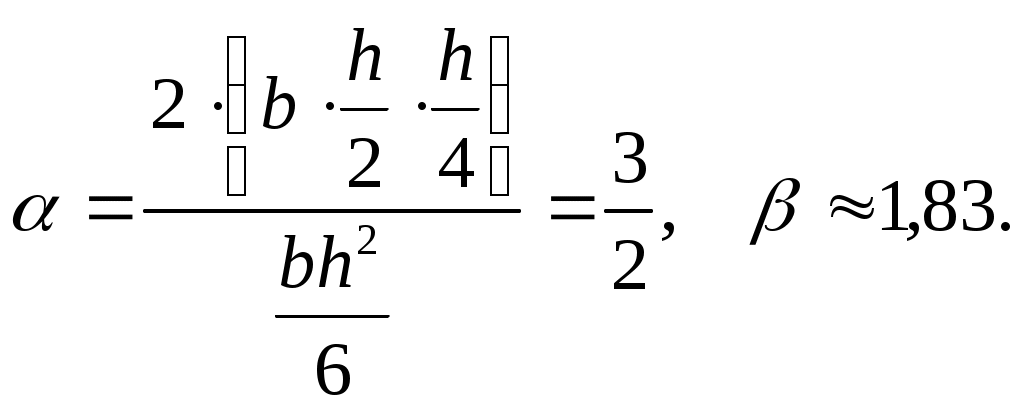
Для двутавровых балок a» 1,16, и при расчете по разрушающим нагрузкам их грузоподъемность увеличивается на 38%.
Вопросы для самопроверки
-
Какие задачи называются статически неопределимыми? -
Почему возникают «лишние» связи? -
Как определяется степень статической неопределимости? -
Какого порядка придерживаются при решении статически неопределимых задач? -
Зачем нужны уравнения совместности деформаций? -
Как выбирают основную систему? -
Как проверяются статически неопределимые балки? -
Почему расчет по допускаемым напряжениям и по допускаемым нагрузкам в некоторых случаях совпадает? -
Какой вид имеет диаграмма для идеального упругопластического материала? -
Как вычисляется пластический момент сопротивления сечения при изгибе?
11. Как вычисляется пластическим моментом сопротивления при кручении?
10. Сложное сопротивление
10.1. Основные понятия
Под сложным сопротивлением подразумевают задачи, в которых брус испытывает одновременное действие различных комбинации растяжения, сжатия, кручения или изгиба.
Чего-либо принципиально нового задачи сложного сопротивления при достаточной жёсткости бруса не вносят. При расчётах на сложное сопротивление используют принцип независимости действия сил, ипоэтому для нахождения полных напряжений и деформаций, возникающих в упругой системе, применяют геометрическое суммирование, как напряжений, так и перемещений, соответствующие различным видам простейших деформаций.
Методика расчёта
Расчёт на прочность и жёсткость складывается из этапов:
-
Построение эпюр в главных плоскостях инерции сечения бруса, для каждого внутреннего силового фактора в отдельности, анализ их и установление опасного сечения. -
Путём исследования напряжённого состояния в опасном сечении устанавливают опасные точки. -
По одной из теорий прочности проводят проверку прочности. -
Прогиб и угол поворота какого-нибудь сечения бруса определяются как геометрические суммы прогибов и углов поворота от составляющих внутренних силовых факторов, действующих в главных плоскостях инерции сечения бруса.
10.2. Косой изгиб
Ранее разобраны такие случаи изгиба, когда внешние силы были расположены в одной из главных центральных плоскостей балки. В этом случае прогибы лежат также в главной центральной плоскости. Такой изгиб назван прямым. Однако в практике встречаются такие случаи, когда внешние силы, будучи перпендикулярными к продольной оси балки и проходящими через центры тяжести поперечных сечений, не совпадают по направлению ни с одной из главных центральных осей инерции поперечных сечений балки. Такой случай изгиба, называемый косым изгибом, имеет некоторые особенности.
10.2.1. Вычисление напряжений и деформаций балок при косом изгибе.
10.2.1. 1. Вычисление напряжений. Условие прочности.
Покажем на примерах метод проверки прочности и вычисления деформаций балок при косом изгибе.
Пример 1. Рассмотрим балку, защемлённую одним концом и нагружённую на другом и посредине силами F1 и F2 , направленными под углами 1, 2 к главной оси у.
Дано: F1 , F2, Ix , Iy, E ,1, 2, l.
Р
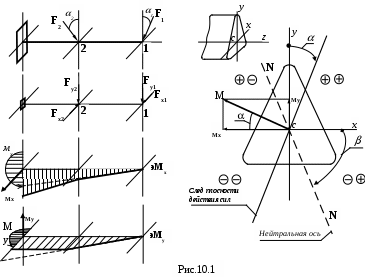
азложим силы на составляющие направленные по главным осям инерции сечения х и у.
Разложим силы на две составляющие по осям по осям координат(рис.10.1): Fх1
, Fх2; Fу1 , Fу2 . Изгибающие моменты Мхи Му в сечении заделки относительно главных осей инерции определим в соответствии с установленным правилом знаков (правило буравчика). Плоскость действия изгибающего момента М не совпадает с главной осью сечения ( у), положение её определяется углом где tqMy / Mx.
Таким образом, в каждом сечении стержня одновременно действуют два изгибающих момента Мхи Му, которые создают изгиб в двух главных плоскостях.
Для определения напряжений от каждого момента в отдельности можно воспользоваться формулой, полученной ранее для плоского изгиба. Пользуясь принципом независимости действия сил, можно написать общую формулу напряжения в произвольной точке, лежащей в положительной четверти осей координат,
По формуле (10.1) можно определить напряжения в любой точке сечения.
Знаки напряжений определяем по физическому смыслу (см. ).
Для проверки прочности необходимо найти точку с наибольшим нормальным напряжением. Пользуясь принципом независимости действия сил, можно считать, что при косом изгибе имеем дело со сложением вращении вокруг двух пересекающихся осей, результирующее движение которых будет поворот сечения вокруг мгновенной оси, которая будет лежать в плоскости ху и проходить через точку пересечения главных осей т.е. через центр тяжести сечения С. Следовательно, мгновенную ось можно считать нулевой линии. Для произвольного сечения необходимо вначале установить положение нулевой линии (N-N), а затем точку, которая дальше других отстоит от этой линии. Положение нулевой линии при косом изгибе установим, приравнять нулю напряжения в точках, принадлежащих этой линии. Пусть текущие координаты нулевой линии будут xNи yN, тогда, применяя формулу (10.1), получим
откуда находим
Обозначим угол наклона нулевой линии к оси