Файл: Методичка по механике вся Печать новый вариант12г.doc

.

Без учета влияния силы тяжести будем искать среднюю скорость пули по формуле:

.

Вычислим:

=113 (м/с)

В вертикальном направлении пуля движется с ускорением силы тяжести, поэтому смещение пробоин в вертикальном направлении равно:

.

Вычислим:

=35 (мкм)

Ответ: 113 м/с; 35 мкм.

№2. Бак в тендере паровоза имеет длину l=4 м. Какова разностьlуровней воды у переднего и заднего концов бака при движении поезда с ускорениема=0,5 м/с²? [20,4 см]

Д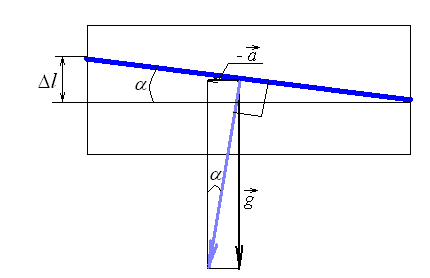ано:

l=4 м

а=0,5 м/с²

Найти: l- ?

Решение.

Рассматривая воду в баке относительно неинерциальной системы отсчета, связанной с ускоренно движущимся вагоном, приходим к необходимости учета силы инерции .

Воспользуемся принципом эквивалентности и построим на рис. векторную сумму ускорений силы тяжести и силы инерции. Поверхность воды в баке будет перпендикулярна этому вектору.

Геометрически находим искомую величину:

.

Вычислим:

0,204 (м)= 20,4 (см).

Ответ: 20,4 см.

Динамика материальной точки, движущейся по окружности

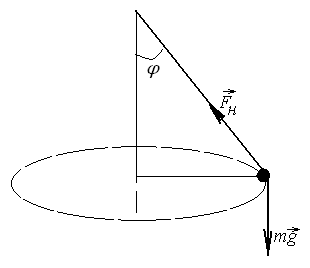№3. Грузик, привязанный к нити длинойl=1 м, описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол=60^оот вертикали. [1,42c]

Дано:

l=1 м

=60^о

Найти: Т-?

Решение. Центростремительное ускорение сообщает грузику результирующая сил тяжести и натяжения нити, точнее горизонтальная составляющая силы натяжения нити (ее вертикальная составляющая компенсирует силу тяжести). По второму закону Ньютона:

.

В проекциях на горизонтальную и вертикальную оси:

,

.

Отсюда



По определению периода имеем:

,

Окончательно:

.

Вычислим:

1,419 (с)1,42 (с).

Ответ: 1,42 с.

Работа и энергия

№4. Насос выбрасывает струю воды диаметром d=2 см со скоростьюv=20 м/с. Найти мощностьN, необходимую для выбрасывания воды. [1,26 кВт,- плотность воды]

Дано:

d=0,02 м

v=20 м/с

Найти: N-?

Решение. По определению мощность измеряется работой, совершаемой за единицу времени. В данном случае работа идет на сообщение кинетической энергии воде. За время tобъем выброшенной воды равен:

,

тогда масса этой воды

.

Ее кинетическая энергия

,

тогда искомая мощность

.

Вычислим:

=1,2610³(Вт)=1,26 (кВт).

Ответ: 1,26 кВт.

№5.Точка совершает гармонические колебания. Наибольшее смещение х_maxточки равно 10 см, наибольшая скорость=20 см/с. Найти угловую частотуколебаний и максимальное ускорениеточки. [2 с^-1; 40 см/с²]

Дано:

х_max=0,1 м

=0,2 м/с

Найти: ,-?

Решение. Запишем уравнение гармонических колебаний:

.

Тогда, дифференцируя, получим закон изменения скорости:

,

тогда

.

Вычислим:

с^-1.

Снова дифференцируем:

.

Вычислим:

(м/с²)= 40 см/с².

Ответ: 40 см/с².

№6. Ареометр массой m=50 г, имеющий трубку диаметромd=1 см, плавает в воде. Ареометр немного погрузили в воду и затем предоставили самому себе, в результате чего он стал совершать гармонические колебания. Найти период Т этих колебаний. [=1.6c,- плотность]

Дано:

m=0,05 г

d=0,01 м

Найти: Т-?

Решение. В состоянии равновесия сила тяжести ареометра компенсируется силой Архимеда, т.к. ареометр и здесь частично погружен в воду. При дополнительном погружении ареометра в воду на величину х(без учета статического смещения) на него начинает действовать добавочная сила, равнаяи направленная к положению равновесия. Отсюда видно, что эта сила – квазиупругая с коэффициентом

,

где - плотность воды, в которой плавает ареометр.

Тогда как для гармонического осциллятора найдем период колебаний ареометра:

.

Вычислим:

=1,601 (с).

Ответ: 1,6 с.

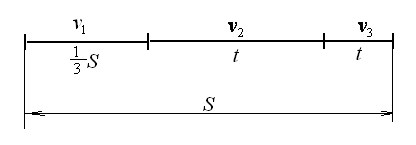
№7. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью =18 км/ч. Далее половину оставшегося времени он ехал со скоростью=22 км/ч, после чего до конечного пункта он шел пешком со скоростью=5 км/ч. Определить среднюю скоростьвелосипедиста.

Получаем: .

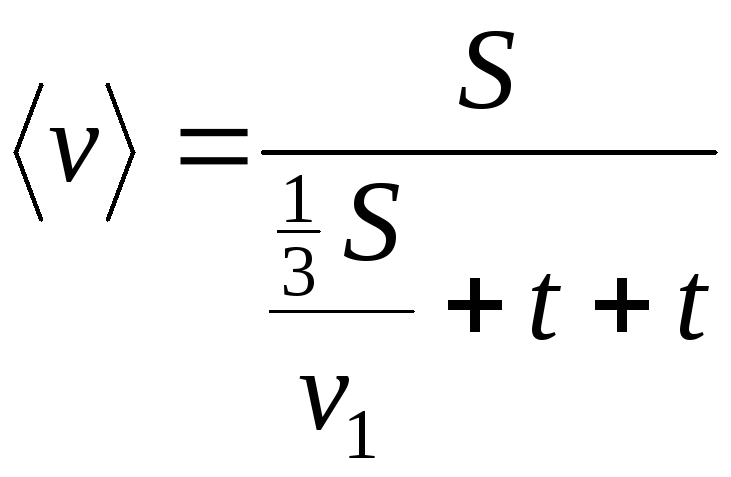Также, сравнивая расстояния, получаем:

.

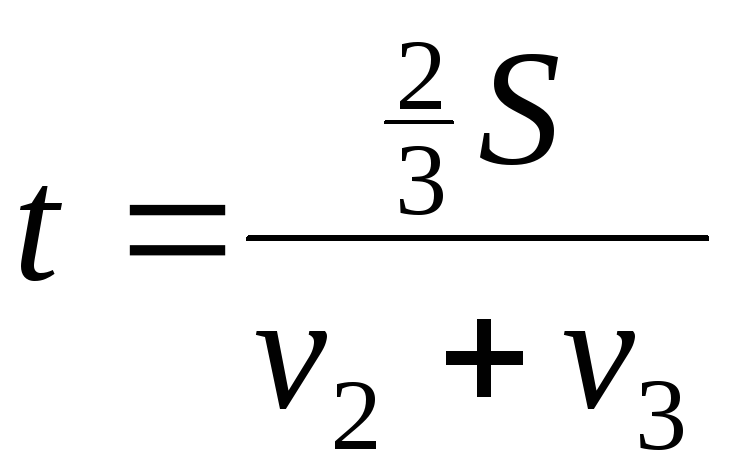Подставляем в равенство для средней скорости:

.

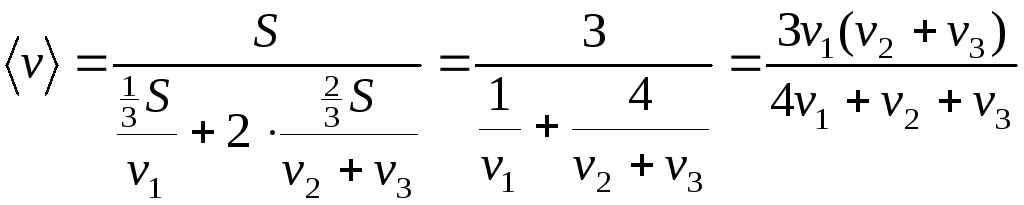Вычисляем:

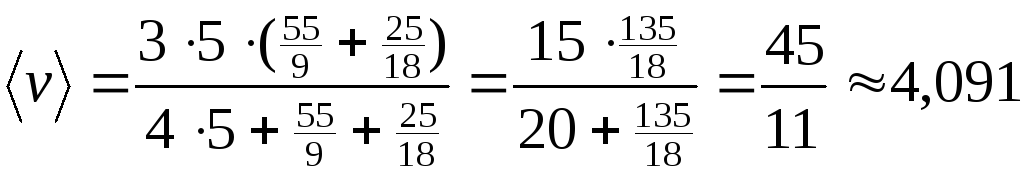(м/с).

Иначе в км/ч:

=14,727 (км/ч)

Ответ: 4,091 м/с или 14,727 км/ч.

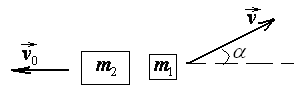
№8. Конькобежец, стоя на коньках на льду, бросает камень массой =2,5 кг под углом=30⁰к горизонту со скоростьюv=10 м/с. Какова будет начальная скоростьдвижения конькобежца, если масса егоm₂=60 кг? Перемещением конькобежца во время броска пренебречь.

,

Отсюда для состояний «до броска» и «после броска» имеем:



 .

Вычислим:

=0,361 (м/с).

Ответ: 0,361 м/с.

№9. Определить КПД неупругого удара бойка массой=0,5 т, падающего на сваю массой=120 кг. Полезной считать энергию, затраченную на вбивание сваи.

.