ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 490
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
6.2.4. Инерционные звенья второго порядка
При k = 1 передаточная
функция звена: W(p) =
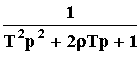 .
.
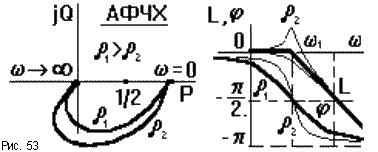
В виду сложности вывода выражений для частотных характеристик рассмотрим их без доказательства, они показаны на рис.53.
Асимптотическая
ЛАЧХ колебательного звена до сопрягающей
частоты
![]() 1= 1/T1совпадает с осью абсцисс, при
дальнейшем увеличении частоты идет с
наклоном - 40 дб/дек. То есть высокие
частоты колебательное звено "заваливает"
сильнее, чем апериодическое звено.
1= 1/T1совпадает с осью абсцисс, при
дальнейшем увеличении частоты идет с
наклоном - 40 дб/дек. То есть высокие
частоты колебательное звено "заваливает"
сильнее, чем апериодическое звено.
Реальная ЛАЧХ при
![]()
![]()
![]() 1значительно отличается от асимптотической.
Это отличие тем существенней, чем меньше
коэффициент демпфирования
1значительно отличается от асимптотической.
Это отличие тем существенней, чем меньше
коэффициент демпфирования![]() .
Точную кривую можно построить,
воспользовавшись кривыми отклонений,
которые приводятся в справочниках. В
предельном случае
.
Точную кривую можно построить,
воспользовавшись кривыми отклонений,
которые приводятся в справочниках. В
предельном случае![]() =
0 получаем консервативное звено, у
которого при
=
0 получаем консервативное звено, у
которого при![]()
![]()
![]() 1амплитуда выходных колебаний стремится
к бесконечности (рис.54).
1амплитуда выходных колебаний стремится
к бесконечности (рис.54).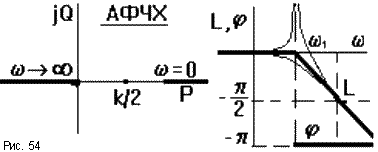
ЛФЧХ при малых частотах асимтотически стремится к нулю. При увеличении частоты до бесконечности выходной сигнал поворачивается по фазе относительно входного на угол, стремящийся в пределе к - 180о. ЛФЧХ можно построить с помощью шаблона, но для этого нужен набор шаблонов для разных коэффициентов демпфирования. При уменьшении коэффициента демпфирования АФЧХ приближается к оси абсцисс и в пределе у консервативного звена она вырождается в два луча по оси абсцисс, при этом фаза выходных колебаний скачком меняется от нуля до - 180опри переходе через сопрягающую частоту (рис.54).
6.2.5. Правила построения чх элементарных звеньев
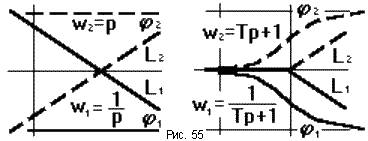
При построении ЧХ некоторых звеньев можно использовать “правило зеркала”: при k = 1 ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно горизонтальной оси. Так на рис.55 изображены ЧХ идеального дифференцирующего и идеального форсирующего звеньев.
Если k![]() 1,
то передаточную функцию звена можно
рассматривать как произведение W = k.W1,
где W1- передаточная функция с k =
1. При этом амплитуда вектора АФЧХ W(j
1,
то передаточную функцию звена можно
рассматривать как произведение W = k.W1,
где W1- передаточная функция с k =
1. При этом амплитуда вектора АФЧХ W(j![]() )
при всех значениях
)
при всех значениях![]() должна
бытьувеличена в k раз, то есть A(
должна
бытьувеличена в k раз, то есть A(![]() )
= kA1(
)
= kA1(![]() ).
Поэтому, например, центр полуокружности
АФЧХ апериодического звена будет
находиться не в точке P = 1/2, а в точке
k/2. ЛАЧХ также изменится: L(
).
Поэтому, например, центр полуокружности
АФЧХ апериодического звена будет
находиться не в точке P = 1/2, а в точке
k/2. ЛАЧХ также изменится: L(![]() )
= 20lgA(
)
= 20lgA(![]() )
= 20lgkA1(
)
= 20lgkA1(![]() )
= 20lgk + 20lgA1(
)
= 20lgk + 20lgA1(![]() ).
Поэтому при k
).
Поэтому при k![]() 1
ЛАЧХ звена нужно поднять по оси ординат
не меняя ее формы на 20lgk. На ЛФЧХ изменение
k никак не отразится.
1
ЛАЧХ звена нужно поднять по оси ординат
не меняя ее формы на 20lgk. На ЛФЧХ изменение
k никак не отразится.
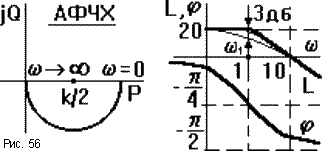
Для примера на рис.56 приведены частотные характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического звена с k = 1 поднята вверх на 20lg10 = 20.
Лекция 7.Чх разомкнутых сау
7.1. Частотные характеристики разомкнутых одноконтурных сау
При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии.
Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУсостоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию.
Передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев:
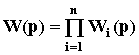 .
.
Заменив в этом выражении p на j w получим ее АФЧХ:
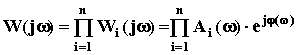 .
.
АЧХ:
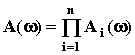 ,
,
значит ЛАЧХ равна
сумме ЛАЧХ звеньев:
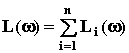 .
.
ЛФЧХ:
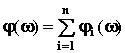 .
.
Таким образом ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем графического сложения ЛАЧХ и ЛФЧХ звеньев. При этом ограничиваются построением асимптотической ЛАЧХ.
Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:
1) раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго);
2) вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена;
3) путем графического суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.
Рассмотрим конкретный пример:
W(p) =
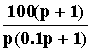 =
W1W2W3W4.
=
W1W2W3W4.
Раскладываем данную передаточную функцию на передаточные функции элементарных звеньев:
1) безынерционное звено:
W1 = K1 = 100 => L(w) = 20lg100 = 40;
2) форсирующее звено:
W2 = p + 1;
его параметры:
K2
= 1, T2
= 1,
![]() 2
= 1/T2
= 1;
2
= 1/T2
= 1;
3) интегрирующее звено:
W3 = 1/p;
его ЛАЧХ проходит
через точку L = 0при частоте
![]() =
1;
=
1;
4) апериодическое звено:
W4 = 1/(0.1p + 1);
его параметры: K4
= 1, T4
= 0.1,
![]() 4
= 1/T4 = 10.
4
= 1/T4 = 10.
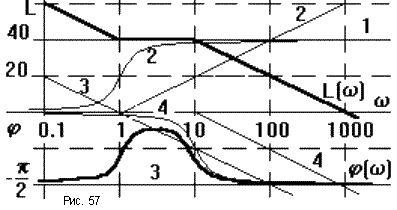
Порядок построения ЛАЧХ и ЛФЧХ показан на рис.57.
Иногда требуется решить обратную задачу, то есть определить передаточную функцию по известной ЛАЧХ. Процедура определения передаточной функции состоит из следующих этапов:
1) известная ЛАЧХ представляется в асимптотическом виде, для этого непрерывная кривая заменяется отрезками прямых либо горизонтальных, либо с наклоном, кратным ±20 дб/дек;
2) асимптотическая ЛАЧХ раскладывается на ЛАЧХ элементарных звеньев;
3) для каждой из
полученных ЛАЧХ определяются kи
![]() 1
= 1/Tи записывается передаточная
функция типового звена;
1
= 1/Tи записывается передаточная
функция типового звена;
4) передаточная функция САУ определяем путем перемножения передаточных функций типовых звеньев.
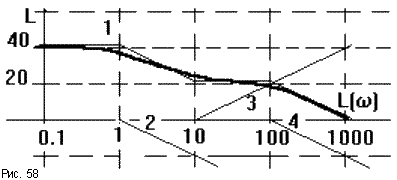
Описанный порядок иллюстрируется на рис.58.
Здесь ЛАЧХ может быть представлена суммой ЛАЧХ четырех типовых звеньев: пропорционального W1 = 100, апериодическогоW2 = 1/(p + 1), форсирующегоW3 = 0.1p + 1и апериодическогоW4 = 1/(0.01p + 1).
Таким образом, передаточная функция разомкнутой САУ имеет вид
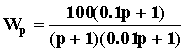 .
.
В более сложных случаях наклоны ЛАЧХ на некоторых участках превышают ± 20дб/дек. Тогда помимо параметров KиTприходится определять еще и коэффициенты демпфированияr.
Зная передаточную функцию разомкнутой САУ можно построить ее уравнение динамики
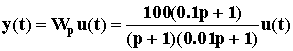 =>
=>![]() =>
=>![]() =>
=>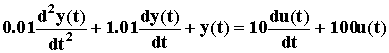 .
.