Файл: kurs-lekcij-po-tau.doc

12.2. Интегральные критерии качества

Интегральные критерии позволяют судить о качестве управления путем вычисления интегралов от некоторых функций управляемой величины. Эта функция выбирается таким путем, чтобы значение определенного интеграла от этой функции по времени от 0до +было однозначно связано с качеством переходного процесса. В то же время данный интеграл должен сравнительно просто вычисляться через коэффициенты уравнений исследуемой системы.

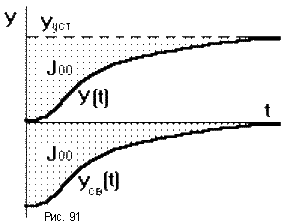
Например, если переходная характеристика является монотонной, то можно утверждать, что качество переходного процесса тем лучше, чем меньше площадь, ограниченная данной кривой и установившимся значением управляемой величины (рис.91). Она равна площади, ограниченной кривой изменения свободной составляющей управляемой величины и осью абсцисс.

Если система устойчива, то свободная составляющая управляемой величины в пределе стремится к нулю, поэтому площадь ограниченная данной кривой имеет конечное значение и определяется по формуле:

J_oo = .

Величина J_ooпредставляет собойлинейную оценку качества управления.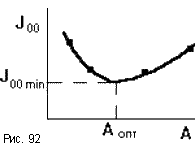

Чем она меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум J_oo.  Если имеется какой то варьируемы параметрA, то можно построить кривую J_oo = f(A)(рис.92). Ее минимум, определяемый из условия dJ_oo/dA = 0, даст оптимальное значениеA.

Пусть дано уравнение динамики замкнутой САУ:  

(a₀pⁿ + a₁p^n-1 + a₂p^n-2 + ... + a_n)y = (b₀p^m + b₁p^m-1 + ... + b_m)u.

Свободный процесс описывается однородным дифференциальным уравнением:

(a₀pⁿ + a₁p^n-1 + ... + a_n)y^св = 0,

следовательно:  

y^св=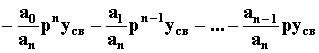

y^св=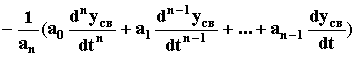

J_oo = св(t)dt =.

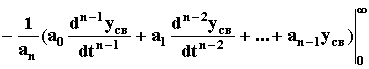Пусть при t = 0 САУ имела следующие начальные условия:

y^св(0) = y₀, = y₀’, ...,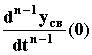= y₀^(n-1).

Кроме того

y^св() = 0,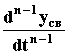() = 0,...,() = 0,

так как процесс затухает и при t свободная составляющая и все производные становятся равны нулю. Подставляя эти значение, получаем:

J_oo = (a₀y₀^(n-1) + a₁y₀^(n-1) + ... + a_n-1y₀)/(a_n.

То есть линейную оценку качества регулирования можно легко вычислить, зная начальные условия и коэффициенты дифференциального уравнения. Возможны и другие линейные оценки качества, но они используются реже, например:

J₀₁ = св(t)tdt;

J_0n = св(t)tⁿdt.

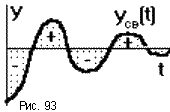
Линейные оценки качества неприменимы при колебательном процессе. Так как площади, ограниченные кривой y^св(t)и осью абсцисс складываются с учетом знака, то минимальному значениюJ_ooможет соответствовать процесс с большим числом колебаний и малым быстродействием (рис.93). В этом случае болееэффективны квадратичные оценки качества, например,

J₂₀ = y^св₂(t)dt.

Значение этого интеграла соответствует площади под кривой y^св₂(t) и осью абсцисс, которая всегда положительна (рис.94).

Выбирая параметры САУ по минимуму J₂₀мы приближаем кривуюy^св(t)к осям координат, что приводит к уменьшению времени регулирования (рис.95). Вывод формулы для вычисления этой оценки сложен, поэтому ограничимся замечанием, что значение  вычисляется через коэффициенты дифференциального уравненияa₀...a_n,b₀...b_m. При вычислении слагаемых в этой формуле используются определители Гурвица, так что даже расчет по ней сопряжен с определенными трудностями и требует использования ЭВМ или специальных таблиц.

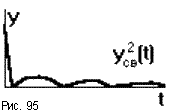
При выборе параметров САУ по минимуму J₂₀часто получают нежелательную колебательность процесса, так как приближениеy^св(t)к оси ординат вызывает резкое увеличение начальной скорости, что в свою очередь может вызвать большое перерегулирование, уменьшив при этом запас устойчивости. Для того, чтобы обеспечить плавность протекания процесса, в квадратичную оценку качества добавляется слагаемое, зависящее от скорости изменения регулируемого параметраy^св’(t). Получаем критерий качества

J₂₁ = св₂(t) + t₂(y^св’(t))₂]dt,

где - некоторая наперед заданная постоянная времени, определяющая весовое соотношение между оценкой поy^сви поy^св’. При малых значениях уменьшение колебательности будет незначительным. Завышениеувеличит время переходного процесса так, что ее выбор определяется конкретными условиями.

Этот интеграл имеет наименьшее значение, если переходный процесс соответствует экспоненте с постоянной времени(рис.96). Другими словами, по соображениям качества управления следует стремиться к тому, чтобы переходная характеристика замкнутой САУ как можно меньше отличалась от характеристики инерционного звена первого порядка, имеющего наперед заданную постоянную времени , значение которой определяются техническими условиями.

Задача выбора параметров САУ по минимуму J₂₀ иJ₂₁решается аналитически только в случае невысокого порядка дифференциального уравнения. Иначе используют ЭВМ.

Лекция 13.Частотные методы оценки качества

13.1. Теоретическое обоснование

Частотные методы основаны на привычном для инженеров графическом изображении динамических характеристик, которые можно снять экспериментально, поэтому они находят широкое применение. В частности зная АФЧХ разомкнутой САУ W_p(j), можно построить АФЧХ замкнутой САУ

Wз(j) ==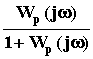 P_з() + jQ_з(),

а по ней - требуемую для частотных методов вещественную ЧХ замкнутой САУ P_з(). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристику САУh(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.

Теоретическое обоснование этого в том, что любую функцию, в том числе и единичную ступенчатую, можно разложить в ряд Фурье:

1(t) = A₀ + A_k1cos(kt) + A_k2sin(kt)].

Так как замкнутая САУ линейна, то при подаче на вход суммы сигналов с выхода снимается сигнал, равный сумме реакций на каждый из входных сигналов. Входному сигналу ui(wi,t) на выходе будет соответствовать составляющая выходного сигнала y_i(_i,t) = W(j_i)u_i(_i,t), тогда