ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 459
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
Недостаток этого способа в том, что астатизм обеспечивается только при строго определенных Kk(p). Любые неточности, особенности из-за изменения параметров в процессе эксплуатации САУ, ведут к появлению статической ошибки, в то время как, астатизм, достигнутый введением интегрирующих звеньев, сохраняется и при изменении параметров САУ.
15.3. Коррекция с использованием неединичной обратной связи
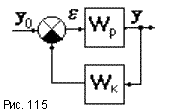
Астатизм САУ относительно задающего воздействия можно обеспечить также использованием неединичной обратной связи, когда корректирующее устройство включается в цепь главной обратной связи (рис.115). При этом
Wэкв(p)
=
.
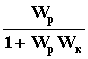В установившемся режиме:
y =
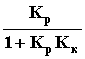yo(p).
Если принять Kk(p)
=
,
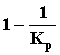то получим
y =
=
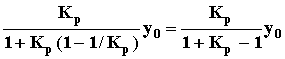yo(p),
то есть Kэкв(p) = 1. Преимущества и недостатки данного способа коррекции те же, что и в предыдущем случае.
15.4. Компенсация возмущающего воздействия
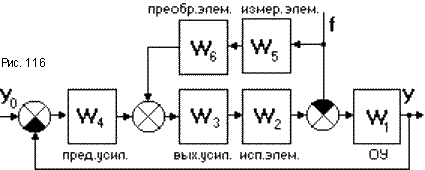
Если возмущающее воздействие доступно измерению, то точность управления можно существенно повысить включив в САУ цепь компенсации возмущающего воздействия (рис.116), обеспечив тем самым комбинированное регулирование. Компенсирующую цепь обычно включают между входным и выходным каскадами усилителя. Составим передаточную функцию относительно возмущающего воздействия:
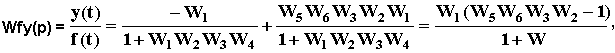
где W = W1
W2
W3
W4- передаточная функция прямой цепи. ЕслиW2
W3
W5
W6
= 1, тоWfy(p)
= 0, то есть любое возмущениеfне
будет оказывать никакого влияния на
выходную величину y. В этом случае
говорят, что регулируемая величинаинвариантна(независима) относительно
возмущенияf.САУ, в которых выходная
величина не зависит от возмущений,
называетсяинвариантной.
Абсолютно
инвариантной САУназывается САУ, в
которойWfy(p)тождественно равна нулю (как в
установившемся, так и в переходном
режимах). Это обеспечить очень сложно,
поэтому обычно ограничиваются упрощенным
исполнением регулятора по возмущению,
что обеспечивает частичное выполнение
принципа инвариантности. При этом
достигается условие
=Kfy<<1, то естьKfy
0и влияние возмущения f на управляемую
величину очень мало. В этом случае
говорят, что достигается инвариантность
с точностью до малой величиныe.
Этот вид регулирования имеет большие достоинства, так как в результате уменьшения влияния возмущения снижаются требования к замкнутому контуру регулирования. Это позволяет уменьшить передаточный коэффициент разомкнутой САУ, а следовательно повысить запас устойчивости замкнутой САУ. Сама компенсирующая цепь не влияет на устойчивость замкнутого контура, но она в свою очередь сама должна быть устойчивой.