ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 447
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
10.2. Понятие запаса устойчивости
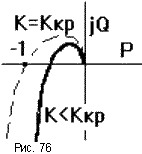
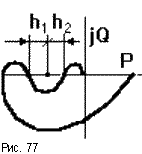
В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.
Согласно критерия Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.
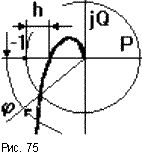
Запас устойчивости по модулюхарактеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием hот критической точки до точки пересечения годографом оси абсцисс (рис.75).
Запас устойчивости
по фазе характеризует удаление
годографа от критической точки по дуге
окружности единичного радиуса и
определяется углом![]() между
отрицательным направлением вещественной
полуоси и лучом, проведенным из начала
координат в точку пересечения годографа
с единичной окружностью.
между
отрицательным направлением вещественной
полуоси и лучом, проведенным из начала
координат в точку пересечения годографа
с единичной окружностью.
Как уже отмечалось, с ростом коэффициента передачи разомкнутой САУ растет модуль каждой точки АФЧХ и при некотором значении K = KкрАФЧХ пройдет через критическую точку (рис.76) и попадет на границу устойчивости, а приK > Kкр замкнутая САУ станет неустойчива. Однако в случае “клювообразных” АФЧХ (получаются из-за наличия внутренних обратных связей) не только увеличение, но и уменьшениеKможет привести к потере устойчивости замкнутых САУ (рис.77). В этом случае запас устойчивости определяется двумя отрезкамиh1иh2, заключенными между критической точкой и АФЧХ.
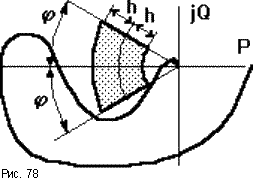
Обычно при создании
САУ задаются требуемыми запасами
устойчивости hи![]() ,
за пределы которых она выходить не
должна. Эти пределы выставляются в виде
сектора, вычерчиваемого вокруг критической
точки, в который АФЧХ разомкнутой САУ
входить не должна (рис.78).
,
за пределы которых она выходить не
должна. Эти пределы выставляются в виде
сектора, вычерчиваемого вокруг критической
точки, в который АФЧХ разомкнутой САУ
входить не должна (рис.78).
10.3. Анализ устойчивости по лчх
Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.
Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K1 < K2. Пусть первая САУ устойчива в замкнутом состоянии, вторая нет.(рис.79).
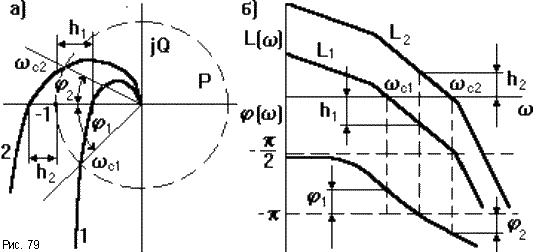
Если W1(p)- передаточная функция первой САУ, то
передаточная функция второй САУW2(p)
= K![]() W1(p),
гдеK = K2/K1.
Вторую САУ можно представить
последовательной цепочкой из двух
звеньев с передаточными функциями K
(безынерционное звено) иW1(p),
поэтому результирующие ЛЧХ строятся
как сумма ЛЧХ каждого из звеньев.
W1(p),
гдеK = K2/K1.
Вторую САУ можно представить
последовательной цепочкой из двух
звеньев с передаточными функциями K
(безынерционное звено) иW1(p),
поэтому результирующие ЛЧХ строятся
как сумма ЛЧХ каждого из звеньев.
Поэтому ЛАЧХ второй
САУ: L2(![]() )
= 20lgK + L1(
)
= 20lgK + L1(![]() ),
),
а ЛФЧХ:
![]() 2(
2(![]() )
=
)
=![]() 1(
1(![]() ).
).
Пересечениям АФЧХ
вещественной оси соответствует значение
фазы
![]() =
-
=
-![]() .
Это соответствует точке пересечения
ЛФЧХ
.
Это соответствует точке пересечения
ЛФЧХ
![]() =
-
=
-![]() линии координатной сетки. При этом, как
видно на АФЧХ, амплитудыA1(
линии координатной сетки. При этом, как
видно на АФЧХ, амплитудыA1(![]() )
< 1, A2(
)
< 1, A2(![]() )
> 1, что соответствует на САЧХ значениямL1(
)
> 1, что соответствует на САЧХ значениямL1(![]() )
= 20lgA1(
)
= 20lgA1(![]() )
< 0 и L2(
)
< 0 и L2(![]() )
> 0.
)
> 0.
Сравнивая АФЧХ и
ЛФЧХ можно заключить, что система в
замкнутом состоянии будет устойчива,
если значению ЛФЧХ
![]() =
-
=
-![]() будут соответствовать отрицательные
значения ЛАЧХ и наоборот. Запасам
устойчивости по модулюh1иh2,
определенным по АФЧХ соответствуют
расстояния от оси абсцисс до ЛАЧХ в
точках, где
будут соответствовать отрицательные
значения ЛАЧХ и наоборот. Запасам
устойчивости по модулюh1иh2,
определенным по АФЧХ соответствуют
расстояния от оси абсцисс до ЛАЧХ в
точках, где
![]() =
-
=
-![]() ,
но в логарифмическом масштабе.
,
но в логарифмическом масштабе.
Особыми точками
являются точки пересечения АФЧХ с
единичной окружностью. Частоты
![]() c1и
c1и
![]() c2,
при которых это происходит называютчастотами среза.
c2,
при которых это происходит называютчастотами среза.
В точках пересечения
A(![]() )
= 1 = > L(
)
= 1 = > L(![]() )
= 0- ЛАЧХ пересекает горизонтальную
ось. Если при частоте среза фаза АФЧХ
)
= 0- ЛАЧХ пересекает горизонтальную
ось. Если при частоте среза фаза АФЧХ
![]() c1
> -
c1
> -![]() (рис.79а кривая 1), то замкнутая САУ
устойчива. На рис.79б это выглядит так,
что пересечению ЛАЧХ горизонтальной
оси соответствует точка ЛФЧХ, расположенная
выше линии
(рис.79а кривая 1), то замкнутая САУ
устойчива. На рис.79б это выглядит так,
что пересечению ЛАЧХ горизонтальной
оси соответствует точка ЛФЧХ, расположенная
выше линии
![]() =
-
=
-![]() .
И наоборот для неустойчивой замкнутой
САУ (рис.79а кривая 2)
.
И наоборот для неустойчивой замкнутой
САУ (рис.79а кривая 2)
![]() c2
<-
c2
<-![]() ,
поэтому при
,
поэтому при
![]() =
=![]() c2ЛФЧХ проходит ниже линии
c2ЛФЧХ проходит ниже линии
![]() =
-
=
-![]() .
Угол
.
Угол
![]() 1
=
1
=
![]() c1-(-
c1-(-![]() )является запасом устойчивости по фазе.
Этот угол соответствует расстоянию от
линии
)является запасом устойчивости по фазе.
Этот угол соответствует расстоянию от
линии
![]() =
-
=
-![]() до ЛФЧХ.
до ЛФЧХ.
Исходя из сказанного,
критерий устойчивости Наквиста по
логарифмическимЧХ, в случаях, когда
АФЧХ только один раз пересекает отрезок
вещественной оси[-![]() ;-1],
можно сформулировать так: для того,
чтобы замкнутая САУ была устойчива
необходимо и достаточно, чтобы частота,
при которой ЛФЧХ пересекает линию
;-1],
можно сформулировать так: для того,
чтобы замкнутая САУ была устойчива
необходимо и достаточно, чтобы частота,
при которой ЛФЧХ пересекает линию
![]() =
-
=
-![]() ,
была больше частоты среза.
,
была больше частоты среза.
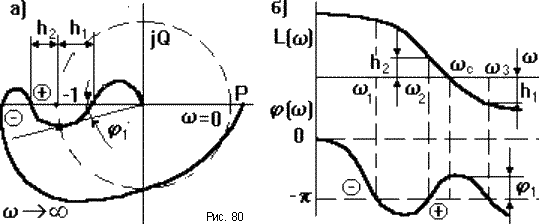
Если АФЧХ разомкнутой
САУ имеет сложный вид (рис.80), то ЛФЧХ
может несколько раз пересекать линию
![]() =
-
=
-![]() .
В этом случае применение критерия
Найквиста несколько усложняется. Однако
во многих случаях данной формулировки
критерия Найквиста оказывается
достаточно.
.
В этом случае применение критерия
Найквиста несколько усложняется. Однако
во многих случаях данной формулировки
критерия Найквиста оказывается
достаточно.
Лекция 11.Качество сау
11.1. Теоретическое обоснование метода d-разбиений
Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.
Приведем характеристическое уравнение замкнутой САУ к виду:
D(p) = pn + c1 pn -1 + c2 pn-2 + ... + cn = 0,
где c0 = a0 /a0 = 1, c1 = a1 /a0 и т.д. При некоторых конкретных значенияхc1 ,c2 ,...,cn уравнение имеет единственное решение, то есть единственный набор корней (p1 , p2 ,...,pn). По их расположению на комплексной плоскости можно судить об устойчивости САУ при заданных параметрах. Если изменить какой-либо параметр САУ, например коэффициента передачи, то изменятся и коэффициенты характеристического уравненияD(p) = 0и станут равнымиcн1 ,cн2 ,...,cнn .Уравнение примет вид: